
6.4.8 Buckling of MWCNTs
Based on the proposed vdW interaction model, the buckling loads for MWCNTs with 2, 5, 10, and 17 layers have been calculated and are presented in Fig. 6.7(A–D). For all of the considered MWCNTs in Fig. 6.7(A–D), the innermost radius RI=11.9 nm. Fig. 6.7(A–D) show the relationship between the buckling loads and the wavenumbers (m, n). The effect of vdW interaction on the buckling loads is examined by comparing the buckling loads with (curves with solid line) and without (curves with dash line) the vdW force taken into consideration. As can be observed in Fig. 6.7A–D, the influence of vdW interaction is more obvious as the number of layers increases. This phenomenon is expected because the critical buckling load always occurs on the outermost layer of an MWCNT, and for a CNT with a fixed innermost radius the more layers there are, the bigger the surface area of the outermost tube. As mentioned above, the force exerted on each carbon atom of the surface of a tube is the sum of the vdW forces from all atoms on the surface of all the other tubes. Thus, the influence of vdW interaction is greater for an MWCNT with a larger radius. With minimization of the buckling loads with respect to the wavenumber m and n, the critical buckling loads are obtained as Ncr=1.1605 N/m for the DWCNT; Ncr=1.1138 N/m for the five-walled CNT; Ncr=1.0432 N/m for the 10-walled CNT; and Ncr=0.9520 N/m for the 17-walled CNT.

Fig. 6.8 shows the dependency of critical buckling loads on the number of layers of an MWCNT. The critical buckling loads decrease as the number of layers increases. This is because the more layers that there are, the larger the outermost radius of an MWCNT, and a larger radius leads to smaller critical axial stress [44]. The effects of vdW interaction before and after buckling are also clearly illustrated in Fig. 6.8. Taking only the initial pressure pij before buckling into account, vdW interaction will be slightly lower for the critical load compared to the critical load without vdW force. This result is coincident with the fact that the presence of the external pressure will reduce the critical axial load of a cylindrical shell [40]. Furthermore, taking into account the prebuckling pressure pij as well as the interaction coefficient cij, vdW interaction results in higher critical loads than those without considering vdW force. For DWCNTs, vdW interaction is insignificant. As the number of layers of an MWCNT increases, the influence of vdW interaction becomes more significant. As explained above, this is because the vdW force is greater for larger CNT surfaces.

In summary, original explicit formulas have been derived for predicting the vdW interaction before and after buckling for MWCNTs under compression. The derived formulas capture the vdW interaction between any two layers of an MWCNT. This refined vdW model indicates that the prebuckling pressures and the vdW interaction coefficients between different two layers are different and strongly dependent on the radius of the tube when the radius is small enough. Moreover, the prebuckling pressures and the vdW interaction coefficients between any two layers approach constant values with increasing radii of the MWCNT. However, the vdW interaction coefficients (or prebuckling pressures) between any two adjacent layers approach the same constant as the radius increases. The derived formulas of the vdW interaction are not only for the buckling problem of MWCNTs, but also for other related topics, such as vibration and bending problems.
Based on the proposed vdW interaction formulas, a continuum cylindrical shell model is presented to investigate the buckling of an MWCNT, in which each tube is treated as an individual cylindrical shell. An exact formula Eq. (6.38) and a simple approximate formula Eq. (6.39) have been derived for the buckling analysis in the special case of a DWCNT. Comparison between the present approximate formula, Eq. (6.39), and the approximate formula of Ru [16] is carried out, and the relative error is 0.49. Hence, the difference between these two approximate formulas is very small. The results from these two approximate formulas show that vdW interaction does not increase the critical buckling load of a DWCNT. However, the results from the exact Eq. (6.38) indicate that vdW interaction does increase the critical buckling load. It is obvious that these two approximate formulas cannot correctly describe the influence of vdW interaction on the buckling load because they ignore the terms related to the ratio of (RO−RI)/RI.
Analysis of the buckling of MWCNTs was carried out using the proposed model. In contrast to the work of Wang et al. [20], where only vdW interaction between two adjacent layers was considered, the buckling behavior was simulated taking into consideration vdW interaction not just between two adjacent layers but between all layers. The effect of tube size on the critical buckling loads of MWCNTs was also examined.
6.5 Vibration Characteristics of CNTs
6.5.1 Donnell Shell Model for the Vibration of MWCNT
The Donnell shell model has been adopted to analyze the free vibration of MWCNT. An MWCNT consists of two or more single CNTs of radius Ri, thickness h, and modulus of elasticity E. The considered MWCNT is empty inside. No internal or external lateral pressures are applied to the tubes except for the pressure caused by vdW interaction [24].
Based on the Donnell shell theory [40], the governing equations for the harmonic vibrations of an MWCNT can be derived as the 3N coupled equations, i.e.,
(6.40)
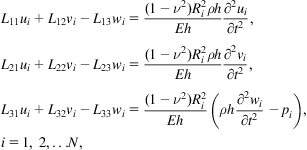 (6.40)
(6.40)
where ui, vi, and wi (i=1, 2, …, N with first layer being the innermost layer and the Nth layer being the outermost layer) are the longitudinal, circumferential, and radial displacement of the ith tube, t is the time, Ri is the radius of tube i, Eh is the in-plane stiffness, ![]() is the mass density per unit area,
is the mass density per unit area, ![]() is Poisson’s ratio, pi is the pressure exerted on the tube i due to vdW interaction between walls, and Lij are the differential operators that are given by
is Poisson’s ratio, pi is the pressure exerted on the tube i due to vdW interaction between walls, and Lij are the differential operators that are given by
(6.41)
 (6.41)
(6.41)
where x and θ are the axial coordinate and the circumferential coordinate, respectively, and D is the effective bending stiffness of a tube. Note that the attractive vdW force is negative and the repulsive vdW force is positive, and the inward pressure is assumed to be positive in Eq. (6.40). Thus, the net pressure due to vdW interaction can be expressed as
(6.42)
where cij is the vdW interaction coefficient [22] and is dependent on Ri.
Let us examine the vibration solutions for MWCNT with any number of layers. The deflection of all tubes is approximated by
(6.43)
 (6.43)
(6.43)
where Ui, Vi, Wi (i=1, 2, …, N) are 3N unknown coefficients, L is the length of the MWCNT, ![]() , m is the axial half wave number, and n is the circumferential wave number.
, m is the axial half wave number, and n is the circumferential wave number.
Substituting Eq. (6.43) into Eq. (6.40) yields 3N equations:
(6.44)
 (6.44)
(6.44)
where I is an identity matrix and the elements in matrix H are
(6.45)
 (6.45)
(6.45)
To determine nonzero solutions of Ui, Vi, and Wi, it is necessary to equate its determinant to zero. Thus, we have the characteristic equation, i.e.,
(6.46)
Solving Eq. (6.46) yields the natural frequencies of the MWCNT for a given set of wave numbers m and n.
6.5.2 Radial Vibration Analysis of MWCNT
It is noted that the interlayer friction is very small [45] and can be neglected. There is no tangential external loading along the axial or the circumferential directions of the CNT. In this case, Donnell’s equation for the radial deflection wi of the ith layer of the MWCNT can be simplified as
(6.47)
 (6.47)
(6.47)
Substitution of the proposed solution in Eq. (6.43) into Eq. (6.47) yields a set of N equations
(6.48)
where
(6.49)
6.5.2.1 Explicit solution for DWCNT
Considering a DWCNT, the system of Eq. (6.48) is reduced to two equations:
(6.50)
and the natural frequencies of the DWCNT are obtained by solving
(6.51)
Due to the fact that from the equilibrium distance, any increase (wi−wj≥0, i, j=1, 2) or decrease (wi−wj≤0) in the distance between the inner and outer tubes will cause an attractive or repulsive vdW force, respectively. Note that we assume the inward pressure to be positive. Thus, from Eq. (6.42) we have c12≤0 and c21≥0, and it is obvious that
(6.52)
and note that
(6.53)
 (6.53)
(6.53)
Hence, one can easily arrive at
(6.54)
Thus, the solution to Eq. (6.51) is given by
(6.55)
and
(6.56)
It is worth mentioning that when the innermost radius is very large, ![]() and
and ![]() , and thus
, and thus ![]() . Hence, we have
. Hence, we have
(6.57)
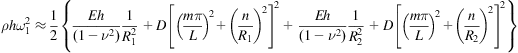 (6.57)
(6.57)
Eq. (6.57) indicates that the effect of the vdW interaction on the lower frequency is very small and then can be neglected when the innermost radius is very large.
The ratios of the amplitudes of the vibration modes associated with ![]() and
and ![]() can be obtained by substituting Eqs. (6.55) and (6.56) into one of Eq. (6.50) and are expressed, respectively, as
can be obtained by substituting Eqs. (6.55) and (6.56) into one of Eq. (6.50) and are expressed, respectively, as
(6.58)
(6.59)
for the second mode. Note that ![]() and
and ![]() , that means the amplitude ratio associated with
, that means the amplitude ratio associated with ![]() is
is ![]() and the amplitude ratio associated with
and the amplitude ratio associated with ![]() is
is ![]() . Thus, for the vibration associated with
. Thus, for the vibration associated with ![]() , both layers are always vibrating in the same direction. In contrast, for the vibration associated with
, both layers are always vibrating in the same direction. In contrast, for the vibration associated with ![]() , both layers are vibrating in the opposite direction always.
, both layers are vibrating in the opposite direction always.
6.5.2.2 Explicit solution for TWCNT
Considering a TWCNT, the system of Eq. (6.48) is reduced to the following three equations:
(6.60)
 (6.60)
(6.60)
Using the condition for the nonzero solutions of W1–W3, one obtains the following determinant equation for the natural frequencies of a TWCNT:
(6.61)
where
(6.62)
 (6.62)
(6.62)
The solutions to Eq. (6.61) are
(6.63)
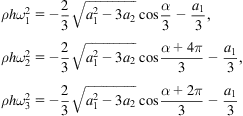 (6.63)
(6.63)
where
(6.64)
The associated amplitude ratios R2,i and R3,i of the TWCNT can be determined as
(6.65)
and
(6.66)
In the examples MWCNTs with an innermost radius RI and an outermost radius RO are analyzed. Each tube has the same length L and is modeled as an individual cylindrical shell. No internal or external lateral pressures are considered for the vibration analysis of the MWCNTs. Following most published papers on CNT, the initial interlayer separation between two adjacent layers is taken as 0.34 nm. The parameters used to calculate the vdW interaction coefficient cij (Ref. [22]) are taken as ε=2.968 meV and σ=3.407 Å [41]. For all examples, the bending and axial stiffnesses of MWCNTs are D=0.85 eV and Eh=360 J/m2 [3], respectively, and the length to the outermost radius ratio is L/RO=10.
Let us first consider a 10-walled MWCNT with innermost radius RI=5 nm. Based on the proposed vdW interaction model, the natural frequencies ![]() which are associated with the radial mode for a 10-walled MWCNT have been calculated by using Eq. (6.48) and are presented in Table 6.3 for various combinations of the wave numbers (m, n). It can be seen from Eq. (6.48) that there are 10 equations that give 10 different natural frequencies f1≤f2≤… fi …≤f9≤f10 for every combination of m and n. Table 6.3 shows that the natural frequencies of the 10-layered MWCNT are very high, in the order of terahertz. As the mode order increases, the lower natural frequencies such as f1, f2, and f3 increase significantly. However, all the other higher natural frequencies, from f4 to f10, are insensitive to the mode order, and thus the effect of the mode order on the higher natural frequencies can be neglected. It should be noted that the natural frequencies for the breathing mode with n=0 are almost the same for various m. This is because the first and third terms in Eq. (6.49) are around 107 times larger than the second term which is related to the wave number m, and thus the influence of the axial half wave number on the natural frequencies is negligible.
which are associated with the radial mode for a 10-walled MWCNT have been calculated by using Eq. (6.48) and are presented in Table 6.3 for various combinations of the wave numbers (m, n). It can be seen from Eq. (6.48) that there are 10 equations that give 10 different natural frequencies f1≤f2≤… fi …≤f9≤f10 for every combination of m and n. Table 6.3 shows that the natural frequencies of the 10-layered MWCNT are very high, in the order of terahertz. As the mode order increases, the lower natural frequencies such as f1, f2, and f3 increase significantly. However, all the other higher natural frequencies, from f4 to f10, are insensitive to the mode order, and thus the effect of the mode order on the higher natural frequencies can be neglected. It should be noted that the natural frequencies for the breathing mode with n=0 are almost the same for various m. This is because the first and third terms in Eq. (6.49) are around 107 times larger than the second term which is related to the wave number m, and thus the influence of the axial half wave number on the natural frequencies is negligible.
Table 6.3
Radial-mode Associated Natural Frequencies (THz) for a 10-Layered MWCNT With Innermost Radius RI=5 nm [24]
| m | n | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 |
| 1 | 0 | 0.5236 | 0.8189 | 1.2606 | 1.7583 | 2.2443 | 2.6907 | 3.0787 | 3.3939 | 3.6254 | 3.7657 |
| 1 | 0.5236 | 0.8189 | 1.2606 | 1.7583 | 2.2443 | 2.6907 | 3.0787 | 3.3939 | 3.6254 | 3.7657 | |
| 6 | 0.5262 | 0.8221 | 1.2623 | 1.7595 | 2.2452 | 2.6914 | 3.0793 | 3.3945 | 3.6259 | 3.7662 | |
| 11 | 0.5515 | 0.8547 | 1.2803 | 1.7717 | 2.2545 | 2.6991 | 3.086 | 3.4005 | 3.6314 | 3.7712 | |
| 16 | 0.6312 | 0.9685 | 1.3485 | 1.8177 | 2.2899 | 2.7283 | 3.1113 | 3.4231 | 3.652 | 3.7908 | |
| 21 | 0.778 | 1.1915 | 1.5195 | 1.9329 | 2.3781 | 2.8012 | 3.1744 | 3.4794 | 3.7029 | 3.8439 | |
| 6 | 0 | 0.5236 | 0.8189 | 1.2606 | 1.7584 | 2.2443 | 2.6907 | 3.0787 | 3.3939 | 3.6254 | 3.7657 |
| 1 | 0.5237 | 0.8189 | 1.2606 | 1.7584 | 2.2443 | 2.6907 | 3.0787 | 3.3939 | 3.6254 | 3.7657 | |
| 6 | 0.5266 | 0.8225 | 1.2625 | 1.7597 | 2.2453 | 2.6915 | 3.0794 | 3.3946 | 3.626 | 3.7662 | |
| 11 | 0.5526 | 0.8557 | 1.2809 | 1.7721 | 2.2549 | 2.6994 | 3.0862 | 3.4007 | 3.6316 | 3.7714 | |
| 16 | 0.6331 | 0.9703 | 1.3497 | 1.8186 | 2.2906 | 2.7289 | 3.1118 | 3.4236 | 3.6524 | 3.7912 | |
| 21 | 0.7804 | 1.1939 | 1.5215 | 1.9343 | 2.3792 | 2.8021 | 3.1752 | 3.4802 | 3.7036 | 3.8446 | |
| 11 | 0 | 0.5238 | 0.819 | 1.2607 | 1.7584 | 2.2443 | 2.6907 | 3.0787 | 3.3939 | 3.6254 | 3.7657 |
| 1 | 0.5238 | 0.819 | 1.2607 | 1.7584 | 2.2443 | 2.6907 | 3.0787 | 3.3939 | 3.6254 | 3.7657 | |
| 6 | 0.5275 | 0.8233 | 1.263 | 1.76 | 2.2456 | 2.6917 | 3.0796 | 3.3947 | 3.6261 | 3.7664 | |
| 11 | 0.5553 | 0.8581 | 1.2824 | 1.7731 | 2.2557 | 2.7001 | 3.0868 | 3.4012 | 3.6321 | 3.7719 | |
| 16 | 0.6376 | 0.9747 | 1.3527 | 1.8207 | 2.2922 | 2.7303 | 3.113 | 3.4247 | 3.6534 | 3.7922 | |
| 21 | 0.7864 | 1.1996 | 1.5263 | 1.9378 | 2.382 | 2.8044 | 3.1772 | 3.482 | 3.7053 | 3.8464 | |
| 16 | 0 | 0.5243 | 0.8193 | 1.2609 | 1.7585 | 2.2445 | 2.6908 | 3.0788 | 3.394 | 3.6255 | 3.7658 |
| 1 | 0.5243 | 0.8194 | 1.2609 | 1.7585 | 2.2445 | 2.6908 | 3.0788 | 3.394 | 3.6255 | 3.7658 | |
| 6 | 0.5293 | 0.8247 | 1.2639 | 1.7606 | 2.2461 | 2.6921 | 3.08 | 3.395 | 3.6264 | 3.7667 | |
| 11 | 0.5598 | 0.8622 | 1.2849 | 1.7749 | 2.257 | 2.7012 | 3.0878 | 3.4021 | 3.6329 | 3.7727 | |
| 16 | 0.6451 | 0.9819 | 1.3576 | 1.8241 | 2.2949 | 2.7325 | 3.115 | 3.4265 | 3.6551 | 3.7939 | |
| 21 | 0.7959 | 1.2088 | 1.534 | 1.9435 | 2.3865 | 2.8082 | 3.1805 | 3.485 | 3.708 | 3.8493 | |
| 21 | 0 | 0.5255 | 0.8201 | 1.2614 | 1.7589 | 2.2448 | 2.691 | 3.079 | 3.3942 | 3.6256 | 3.7659 |
| 1 | 0.5257 | 0.8203 | 1.2615 | 1.759 | 2.2448 | 2.6911 | 3.079 | 3.3942 | 3.6257 | 3.766 | |
| 6 | 0.5324 | 0.8271 | 1.2654 | 1.7617 | 2.2469 | 2.6928 | 3.0805 | 3.3956 | 3.6269 | 3.7671 | |
| 11 | 0.5665 | 0.868 | 1.2885 | 1.7774 | 2.259 | 2.7029 | 3.0893 | 3.4034 | 3.6341 | 3.7738 | |
| 16 | 0.6556 | 0.992 | 1.3645 | 1.829 | 2.2988 | 2.7357 | 3.1178 | 3.429 | 3.6574 | 3.7962 | |
| 21 | 0.8093 | 1.2215 | 1.5446 | 1.9513 | 2.3927 | 2.8134 | 3.1851 | 3.4891 | 3.7118 | 3.8533 |

In Table 6.4 a comparison is made between the results for the radial modes of a five-walled CNT with three inner radii using the present multilayer interaction of vdW forces and the results which are obtained using the single neighboring layer on each side, as was used in Ref. [32]. It can be seen that the additional coupling that exists in the present model between remote layers will lead to higher frequencies for all the CNTs in this table. The differences are in the range of 0–5% and one cannot predict for which case the influence will be larger, as there are several coupling effects involved. In general the second, third, and fourth radial frequencies have larger differences as the radii are reduced.
Table 6.4
Radial Natural Frequencies (THz) of a Five-Walled CNT With L/RO=10: Present vdW Interaction Model Compared to the Model in Ref. [32] for m=1, n=0 [24]
| RI=0.5 nm | RI=1 nm | RI=5 nm | |||||||
| Present | Ref. [32] | % | Present | Ref. [32] | % | Present | Ref. [32] | % | |
| 2.1850 | 2.1620 | 1.06 | 1.7510 | 1.7370 | 0.81 | 0.6183 | 0.6181 | 0.03 | |
| 3.3690 | 3.2500 | 3.66 | 2.7210 | 2.6490 | 2.72 | 1.2960 | 1.2710 | 1.97 | |
| 4.1580 | 3.9520 | 5.21 | 3.4040 | 3.2770 | 3.88 | 2.2710 | 2.1820 | 4.08 | |
| 5.0370 | 4.8320 | 4.25 | 3.9190 | 3.7260 | 5.18 | 3.1010 | 2.9430 | 5.37 | |
| 7.3600 | 7.2600 | 1.38 | 4.4320 | 4.2020 | 5.47 | 3.6410 | 3.4370 | 5.94 | |

To show the effect of vdW interaction on natural frequencies of an MWCNT of small radius, natural frequencies that are associated with the radial mode for a TWCNT with innermost radius RI=0.65 nm are calculated by using Eq. (6.63), and the comparison of the results by considering and ignoring the vdW interaction is presented in Table 6.5(A) for various combinations of the wave numbers (m, n). It is observed that the vdW interaction has a significant effect on the frequencies, especially on the lower frequencies when the innermost radius is very small. Also, it can be seen that the wave number n has a dominant influence on the frequencies. This is because all the three terms in Eq. (6.49) are in the same order when the innermost radius RI is very small, e.g., RI≤1 nm, and thus the effects of the vdW interaction and the mode order must be taken into consideration.
Table 6.5
Comparison of the Influence of the vdW Interaction on the Radial-Mode Associated Natural Frequencies (THz) for a TWCNT With Innermost Radius [24]
| vdW Interaction Is Considered | Without vdW Interaction | ||||||
| m | n | f1 | f2 | f3 | f1 | f2 | f3 |
| (A) RI=0.65 nm | |||||||
| 1 | 1 | 2.9603 | 4.462 | 5.8611 | 2.6381 | 3.5444 | 5.3996 |
| 6 | 3.3122 | 5.117 | 8.1387 | 2.9697 | 4.3134 | 7.8499 | |
| 11 | 5.5419 | 9.3774 | 20.0049 | 5.2825 | 8.9855 | 19.896 | |
| 16 | 10.179 | 18.0186 | 40.9221 | 10.0319 | 17.8216 | 40.8694 | |
| 21 | 16.9671 | 30.4086 | 70.0237 | 16.8782 | 30.2927 | 69.993 | |
| 6 | 1 | 2.9651 | 4.466 | 5.866 | 2.6433 | 3.5494 | 5.4051 |
| 6 | 3.3705 | 5.18 | 8.2303 | 3.0319 | 4.3892 | 7.9452 | |
| 11 | 5.6505 | 9.4924 | 20.1299 | 5.396 | 9.1056 | 20.0217 | |
| 16 | 10.3033 | 18.1452 | 41.0514 | 10.158 | 17.9496 | 40.9988 | |
| 21 | 17.0954 | 30.5377 | 70.1539 | 17.0072 | 30.4224 | 70.1232 | |
| 11 | 1 | 3.0006 | 4.4917 | 5.8901 | 2.6827 | 3.5815 | 5.4315 |
| 6 | 3.5279 | 5.3435 | 8.457 | 3.2001 | 4.5834 | 8.1807 | |
| 11 | 5.9179 | 9.7733 | 20.4337 | 5.6747 | 9.3985 | 20.3272 | |
| 16 | 10.6056 | 18.4528 | 41.3653 | 10.4645 | 18.2605 | 41.3131 | |
| 21 | 17.4072 | 30.8515 | 70.4698 | 17.3205 | 30.7373 | 70.4393 | |
| 16 | 1 | 3.1231 | 4.5776 | 5.9628 | 2.8184 | 3.6884 | 5.5108 |
| 6 | 3.8181 | 5.6304 | 8.8287 | 3.5099 | 4.9182 | 8.5656 | |
| 11 | 6.352 | 10.2238 | 20.9171 | 6.125 | 9.8667 | 20.8131 | |
| 16 | 11.0875 | 18.942 | 41.8639 | 10.9525 | 18.7547 | 41.8124 | |
| 21 | 17.9026 | 31.3499 | 70.9717 | 17.8183 | 31.2376 | 70.9414 | |
| 21 | 1 | 3.4065 | 4.7797 | 6.1286 | 3.1288 | 3.936 | 5.6905 |
| 6 | 4.2793 | 6.07 | 9.3583 | 3.9989 | 5.4196 | 9.1118 | |
| 11 | 6.9619 | 10.8489 | 21.5811 | 6.7544 | 10.5137 | 21.4803 | |
| 16 | 11.7509 | 19.6135 | 42.5475 | 11.6235 | 19.4328 | 42.4968 | |
| 21 | 18.5823 | 32.0332 | 71.6595 | 18.5011 | 31.9233 | 71.6295 | |
| (B) RI=5 nm | |||||||
| 1 | 1 | 0.6574 | 1.9721 | 3.3364 | 0.6176 | 0.657 | 0.7016 |
| 6 | 0.6629 | 1.974 | 3.3374 | 0.6222 | 0.6624 | 0.7082 | |
| 11 | 0.7166 | 1.9935 | 3.3486 | 0.6667 | 0.7157 | 0.7727 | |
| 16 | 0.8916 | 2.0664 | 3.3909 | 0.8143 | 0.89 | 0.9804 | |
| 21 | 1.2242 | 2.242 | 3.4962 | 1.1032 | 1.2251 | 1.3724 | |
| 6 | 1 | 0.6575 | 1.9721 | 3.3364 | 0.6177 | 0.657 | 0.7017 |
| 6 | 0.6638 | 1.9743 | 3.3376 | 0.6231 | 0.6633 | 0.7093 | |
| 11 | 0.7195 | 1.9945 | 3.3492 | 0.6694 | 0.7185 | 0.7758 | |
| 16 | 0.8964 | 2.0686 | 3.3922 | 0.819 | 0.8948 | 0.9854 | |
| 21 | 1.2302 | 2.2454 | 3.4983 | 1.1091 | 1.2312 | 1.3786 | |
| 11 | 1 | 0.658 | 1.9723 | 3.3365 | 0.6182 | 0.6575 | 0.7022 |
| 6 | 0.6665 | 1.9752 | 3.3382 | 0.6256 | 0.666 | 0.712 | |
| 11 | 0.7267 | 1.9972 | 3.3508 | 0.6763 | 0.7258 | 0.7833 | |
| 16 | 0.9082 | 2.0738 | 3.3954 | 0.8305 | 0.9067 | 0.9977 | |
| 21 | 1.2448 | 2.2537 | 3.5036 | 1.1236 | 1.2459 | 1.3936 | |
| 16 | 1 | 0.6597 | 1.9728 | 3.3368 | 0.62 | 0.6592 | 0.7038 |
| 6 | 0.6715 | 1.9769 | 3.3392 | 0.6306 | 0.671 | 0.7172 | |
| 11 | 0.7388 | 2.0017 | 3.3535 | 0.688 | 0.7379 | 0.796 | |
| 16 | 0.9273 | 2.0825 | 3.4006 | 0.8492 | 0.926 | 1.0175 | |
| 21 | 1.268 | 2.2672 | 3.5121 | 1.1467 | 1.2695 | 1.4175 | |
| 21 | 1 | 0.6639 | 1.9742 | 3.3376 | 0.6245 | 0.6634 | 0.7078 |
| 6 | 0.6803 | 1.9799 | 3.341 | 0.6392 | 0.6798 | 0.726 | |
| 11 | 0.7568 | 2.0085 | 3.3575 | 0.7055 | 0.7559 | 0.8146 | |
| 16 | 0.9542 | 2.0949 | 3.4081 | 0.8756 | 0.953 | 1.0453 | |
| 21 | 1.3001 | 2.2861 | 3.5241 | 1.1788 | 1.302 | 1.4505 | |
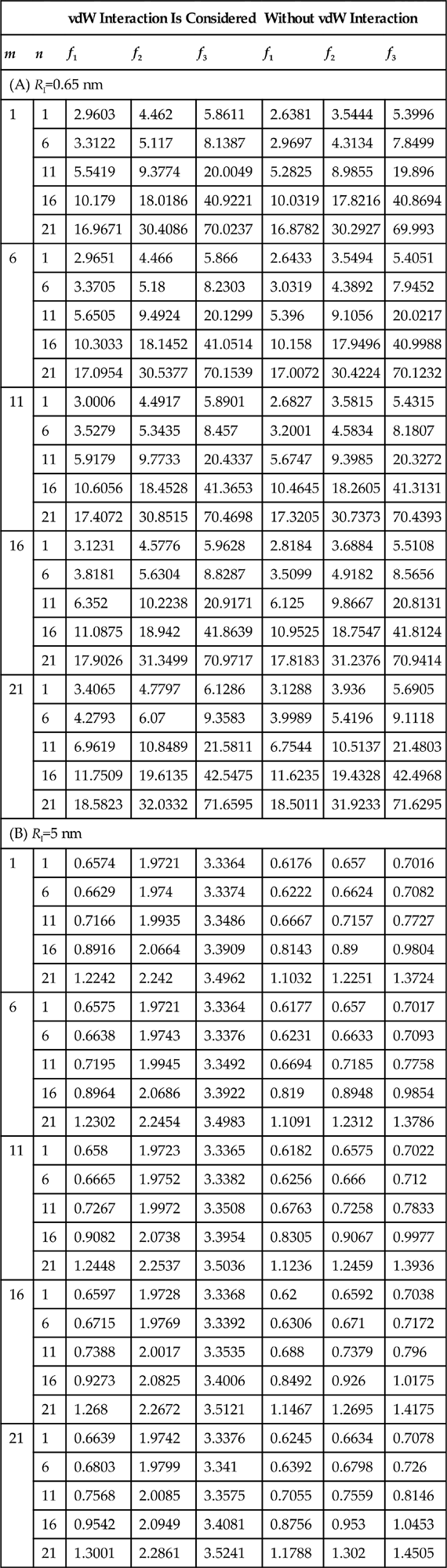
Table 6.5(B) shows the comparison of radial-mode associated frequencies of a TWCNT with large radius for various combinations of (m, n). In contrast to the TWCNT of small radius, the effect of vdW interaction on the lowest frequency is very small and is negligible due to the fact that the effect of the vdW interaction on the lowest frequency that is associated with the radial mode is very small when the innermost radius is large, as indicated in Eq. (6.57) for a DWCNT of big radius. However, the effect of vdW interaction is significant on the higher frequencies for various combinations of (m, n), which is obvious from Eq. (6.49) that when the innermost radius is big, the term related to the vdW interaction coefficient dominates.
Natural frequencies of a DWCNT, a TWCNT, and a five-walled MWCNT are calculated from Eq. (6.44) for various m and n as well as the innermost radii RI=5, 1, and 0.5 nm, and shown in Table 6.6(A)–(C) for the DWCNT, Table 6.7(A)–(C) for the TWCNT, and Table 6.8(A)–(C) for the five-walled MWCNT. It should be noted that n=0 represents the breathing vibration of MWCNTs. In Table 6.6(A)–(C) the modes are also identified by the letters L, T, and R and their combinations to indicate the dominance of the longitudinal, torsional, and radial modes in the various modes. In most cases one can see that the modes are not purely of type L, T, or R, but rather a combination of these where the more dominant one is put first. As can be seen from these tables the frequencies increase as n is increased except for the lowest frequency which decreases first and then increases with the increase of n. Similarly, all the frequencies increase as m is increased. It is clear from the tables that there are changes of mode shapes for the same order of frequency when m or n are changed. For example, in Table 6.6(A), the mode shape of the DWCNT associated with ![]() is mainly torsional mode for the combination of m=1 and n=1, but the mode shape becomes mostly radial mode for the combination of m=1 and n=2. In addition, the frequencies increase significantly with the increase of the radius of MWCNTs, especially the frequencies associated with higher number of n. Also, it can be seen from Tables 6.6–6.8 that for MWCNTs with the same size but different numbers of layers, the highest frequency for the DWCNT, the TWCNT, and the five-walled MWCNT is almost the same, and thus the differences between the lowest and highest frequencies are almost the same for an MWCNT with different numbers of layers. This indicates that the more layers there are, the closer the natural frequencies will be.
is mainly torsional mode for the combination of m=1 and n=1, but the mode shape becomes mostly radial mode for the combination of m=1 and n=2. In addition, the frequencies increase significantly with the increase of the radius of MWCNTs, especially the frequencies associated with higher number of n. Also, it can be seen from Tables 6.6–6.8 that for MWCNTs with the same size but different numbers of layers, the highest frequency for the DWCNT, the TWCNT, and the five-walled MWCNT is almost the same, and thus the differences between the lowest and highest frequencies are almost the same for an MWCNT with different numbers of layers. This indicates that the more layers there are, the closer the natural frequencies will be.
Table 6.6
Natural Frequencies (THz) of a DWCNT With Innermost Radius [24]
| Natural frequencies (THz) | m=1 | m=2 | m=3 | ||||||||||||
| n=0 | n=1 | n=2 | n=3 | n=4 | n=0 | n=1 | n=2 | n=3 | n=4 | n=0 | n=1 | n=2 | n=3 | n=4 | |
| (A) RI=5 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.0391 | 0.0163 | 0.0226 | 0.0393 | … | 0.1248 | 0.0509 | 0.0334 | 0.0424 | … | 0.2210 | 0.1021 | 0.0581 | 0.0519 |
| T&R | R&T | R&T | R&T | T&R&L | R&T | R&T | R&T | R&T&L | R&T | R&T | R&T | ||||
| ω2 | … | 0.4423 | 0.8440 | 1.2540 | 1.6670 | … | 0.4961 | 0.8782 | 1.2760 | 1.6830 | … | 0.5729 | 0.9266 | 1.3110 | 1.7080 |
| L&T | L | L | L | L&T | L&T | L&T | L&T | L&T | L&T&R | L&T&R | L&T | ||||
| ω3 | 0.2018 | 0.4793 | 0.8998 | 1.3380 | 1.7800 | 0.3999 | 0.5769 | 0.9372 | 1.3590 | 1.7940 | 0.5741 | 0.6912 | 0.9972 | 1.3940 | 1.8180 |
| L | L&R | L | L | L | L | L&R | L&T&R | L&T | L&T | L | L&R&T | L&T&R | L&T&R | L&T | |
| ω4 | 0.2061 | 0.6883 | 1.3130 | 1.9130 | 2.3750 | 0.4123 | 0.7773 | 1.3620 | 1.9440 | 2.3930 | 0.6184 | 0.9048 | 1.4380 | 1.9960 | 2.4210 |
| L | T&L | T&R&L | T&R | T&R | L | T&L | T&L&R | T&R&L | T&R&L | L | L&T | T&L&R | T&R&L | R&T&L | |
| ω5 | 0.6802 | 0.9708 | 1.5360 | 2.1670 | 2.7910 | 0.6865 | 1.0010 | 1.5670 | 2.1920 | 2.8100 | 0.7174 | 1.0590 | 1.6190 | 2.2330 | 2.8420 |
| R | T&R | T&R | T&R | T&R | R | R&T&L | T&R&L | T&R&L | T&R | R | T&R&L | T&R&L | T&R&L | T&R&L | |
| ω6 | 2.7570 | 2.7620 | 2.7830 | 2.8470 | 3.0810 | 2.7570 | 2.7620 | 2.7840 | 2.8490 | 3.0920 | 2.7570 | 2.7620 | 2.7840 | 2.8530 | 3.1090 |
| R | R | R | R&T | T&R | R | R | R&T | R&T | T&R | R | R | R&T | R&T | T&R&L | |
| (B) RI=1 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.1508 | 0.1950 | 0.4455 | 0.7981 | … | 0.4749 | 0.2714 | 0.4635 | 0.8095 | … | 0.8515 | 0.4369 | 0.5106 | 0.8326 |
| T&R&L | R&T | R&T | R&T | T&R&L | R&T | R&T | R&T | R&T&L | R&T | R&T | R&T | ||||
| ω2 | … | 1.5790 | 2.3540 | 2.5780 | 2.7450 | … | 1.6230 | 2.3380 | 2.5760 | 2.7470 | … | 1.8150 | 2.3490 | 2.5790 | 2.7530 |
| T&R&L | R&T&L | R&T | R&T | T&R&L | R&T&L | R&T | R&T | T&R&L | R&T&L | R&T | R&T | ||||
| ω3 | 0.8046 | 1.9360 | 3.3890 | 5.0060 | 6.6490 | 1.5980 | 2.3510 | 3.5950 | 5.1170 | 6.7230 | 2.3300 | 2.8170 | 3.8760 | 5.2910 | 6.8440 |
| L | L&T&R | L&R | L | L | L | L&R&T | L&R | L&T&R | L&T | L | L&R&T | L&R&T | L&T&R | L&T&R | |
| ω4 | 0.8128 | 2.3990 | 4.4930 | 6.6850 | 8.8940 | 1.6230 | 2.7990 | 4.6490 | 6.7690 | 8.9500 | 2.4240 | 3.2800 | 4.8830 | 6.9030 | 9.0420 |
| L | L&T&R | L | L | L | L | L&R&T | L&R | L&T | L | L | L&R&T | L&R&T | L&T&R | L&T | |
| ω5 | 2.8960 | 3.9380 | 5.9540 | 8.3340 | 10.830 | 2.9160 | 4.0380 | 6.0740 | 8.4370 | 10.920 | 3.0010 | 0.2380 | 6.2780 | 8.6080 | 11.060 |
| R | R&T | T&R&L | T&R | T&R | R | R&T&L | T&R&L | T&R&L | T&R&L | R | T&R&L | T&R&L | T&R&L | T&R&L | |
| ω6 | 4.2450 | 0.2500 | 7.9340 | 11.140 | 14.500 | 4.2530 | 5.3150 | 8.0240 | 11.220 | 14.560 | 4.2700 | 5.4390 | 8.1760 | 11.350 | 14.670 |
| R | R&T | T&R | T&R | T&R | R | R&T&L | T&R&L | T&R&L | T&R&L | R | R&T&L | T&R&L | T&R&L | T&R&L | |
| (C) RI=0.5 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.2602 | 0.6339 | 1.3380 | 2.0310 | … | 0.7415 | 0.7112 | 1.3640 | 2.0530 | … | 1.3150 | 0.9085 | 1.4270 | 2.0950 |
| T&R&L | R&T | R&T | R&T | T&R&L | R&T | R&T | R&T | R&T&L | R&T&L | R&T | R&T | ||||
| ω2 | … | 1.8250 | 2.5370 | 3.2720 | 4.7150 | … | 1.9080 | 2.5440 | 3.2870 | 4.7380 | … | 2.2110 | 2.5890 | 3.3180 | 4.7760 |
| T&R&L | R&T | R&T | R&T | T&R&L | R&T | R&T | R&T | T&R&L | R&T&L | R&T | R&T | ||||
| ω3 | 1.2840 | 2.9650 | 5.3950 | 7.9840 | 10.610 | 2.5500 | 3.6420 | 5.7020 | 8.1580 | 10.720 | 3.6990 | 4.3850 | 6.1370 | 8.4310 | 10.920 |
| L | L&R&T | L&R | L | L | L | L&R | L&R&T | L&T&R | L&T | L | L&R&T | L&R&T | L&T&R | L&T&R | |
| ω4 | 1.2900 | 4.6330 | 8.9420 | 13.280 | 17.270 | 2.5720 | 5.1380 | 9.1360 | 13.440 | 17.410 | 3.8390 | 5.8110 | 9.4400 | 13.630 | 17.630 |
| L | L&R | L | T&R | T&R | L | L&R | L&R | T&R&L | T&R&L | L | L&R | L&R&T | L&T&R | T&R&L | |
| ω5 | 4.4590 | 6.0840 | 9.4370 | 13.350 | 17.770 | 4.4930 | 6.2630 | 9.6350 | 13.460 | 17.850 | 4.6490 | 0.6220 | 9.9710 | 13.720 | 17.960 |
| R | R&T&L | T&R&L | L | L | R | T&R&L | T&R&L | L&T | L | R | T&R&L | T&R&L | T&R&L | L&T | |
| ω6 | 7.3670 | 10.080 | 15.770 | 22.240 | 28.980 | 7.3820 | 10.180 | 15.880 | 22.340 | 29.060 | 7.4150 | 10.360 | 16.080 | 22.510 | 29.200 |
| R | R&T | T&R | T&R | T&R | R | R&T&L | T&R&L | T&R&L | T&R | R | T&R&L | T&R&L | T&R&L | T&R&L | |

Table 6.7
Natural Frequencies (THz) of a TWCNT With Innermost Radius [24]
| Natural frequencies (THz) | m=1 | m=2 | m=3 | ||||||||||||
| n=0 | n=1 | n=2 | n=3 | n=4 | n=0 | n=1 | n=2 | n=3 | n=4 | n=0 | n=1 | n=2 | n=3 | n=4 | |
| (A) RI=5 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.0359 | 0.0150 | 0.0212 | 0.0370 | … | 0.1155 | 0.0469 | 0.0310 | 0.0398 | … | 0.2059 | 0.0942 | 0.0536 | 0.0483 |
| ω2 | … | 0.4129 | 0.7918 | 1.1780 | 1.5660 | … | 0.4623 | 0.8205 | 1.1960 | 1.5750 | … | 0.5338 | 0.8630 | 1.2240 | 1.5900 |
| ω3 | … | 0.4395 | 0.8417 | 1.2530 | 1.6670 | … | 0.4887 | 0.8720 | 1.2720 | 1.6800 | … | 0.5575 | 0.9165 | 1.3030 | 1.7030 |
| ω4 | 0.1898 | 0.4692 | 0.8963 | 1.3360 | 1.7500 | 0.3764 | 0.5544 | 0.9239 | 1.3500 | 1.7440 | 0.5440 | 0.6609 | 0.9721 | 1.3740 | 1.7480 |
| ω5 | 0.1936 | 0.6355 | 1.1900 | 1.6100 | 1.7930 | 0.3872 | 0.7214 | 1.2370 | 1.6360 | 1.8240 | 0.5807 | 0.8428 | 1.3090 | 1.6760 | 1.8610 |
| ω6 | 0.1939 | 0.6843 | 1.3120 | 1.9200 | 2.4890 | 0.3878 | 0.7640 | 1.3540 | 1.9490 | 2.5100 | 0.5816 | 0.8795 | 1.4230 | 1.9950 | 2.5440 |
| ω7 | 0.6587 | 0.9413 | 1.4870 | 2.0570 | 2.6300 | 0.6642 | 0.9686 | 1.5150 | 2.0780 | 2.6480 | 0.6893 | 1.0220 | 1.5620 | 2.1130 | 2.6790 |
| ω8 | 1.9720 | 1.9860 | 2.0550 | 2.3330 | 2.9070 | 1.9720 | 1.9870 | 2.0580 | 2.3470 | 2.9230 | 1.9720 | 1.9880 | 2.0630 | 2.3700 | 2.9500 |
| ω9 | 3.3360 | 3.3390 | 3.3480 | 3.3710 | 3.4330 | 3.3360 | 3.3390 | 3.3490 | 3.3710 | 3.4350 | 3.3360 | 3.3390 | 3.3490 | 3.3720 | 3.4380 |
| (B) RI=1 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.1145 | 0.1578 | 0.3601 | 0.6334 | … | 0.3628 | 0.2121 | 0.3719 | 0.6403 | … | 0.6562 | 0.3351 | 0.4041 | 0.6550 |
| ω2 | … | 1.1780 | 1.6720 | 1.8390 | 2.0070 | … | 1.2100 | 1.6660 | 1.8390 | 2.0080 | … | 1.3510 | 1.6770 | 1.8420 | 2.0130 |
| ω3 | … | 1.5020 | 2.6710 | 3.0920 | 3.2340 | … | 1.6350 | 2.6900 | 3.0840 | 3.2330 | … | 1.7760 | 2.6970 | 3.0780 | 3.2330 |
| ω4 | 0.6419 | 1.6580 | 2.8230 | 3.9940 | 5.3030 | 1.2770 | 1.9020 | 2.9320 | 4.0860 | 5.3630 | 1.8730 | 2.2730 | 3.1380 | 4.2270 | 5.4610 |
| ω5 | 0.6466 | 2.0030 | 3.3780 | 4.9940 | 6.6400 | 1.2900 | 2.3090 | 3.5460 | 5.0700 | 6.6890 | 1.9280 | 2.6960 | 3.7690 | 5.1900 | 6.7680 |
| ω6 | 0.6509 | 2.3390 | 4.4730 | 6.6580 | 8.6450 | 1.3010 | 2.6230 | 4.5750 | 6.7280 | 8.7120 | 1.9480 | 2.9850 | 4.7330 | 6.8160 | 8.8240 |
| ω7 | 2.3920 | 3.2030 | 4.7820 | 6.6750 | 8.8870 | 2.4070 | 3.2800 | 4.8740 | 6.7390 | 8.9230 | 2.4620 | 3.4330 | 5.0320 | 6.8740 | 8.9820 |
| ω8 | 3.5710 | 4.3270 | 6.0350 | 8.3510 | 10.830 | 3.5770 | 4.3630 | 6.1040 | 8.4150 | 10.890 | 3.5900 | 4.4330 | 6.2210 | 8.5210 | 10.980 |
| ω9 | 4.3960 | 5.2580 | 7.9230 | 11.130 | 14.490 | 4.4000 | 5.2960 | 7.9800 | 11.180 | 14.530 | 4.4070 | 5.3670 | 8.0750 | 11.260 | 14.600 |
| (C) RI=0.5 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.1800 | 0.4563 | 0.8863 | 1.2800 | … | 0.5055 | 0.5025 | 0.8999 | 1.2910 | … | 0.8972 | 0.6289 | 0.9356 | 1.3120 |
| ω2 | … | 1.3130 | 1.8750 | 2.5080 | 3.0910 | … | 1.3660 | 1.8780 | 2.5130 | 3.0960 | … | 1.5540 | 1.9040 | 2.5260 | 3.1070 |
| ω3 | … | 1.9960 | 2.9260 | 3.4470 | 4.7250 | … | 2.0320 | 2.9130 | 3.4500 | 4.7360 | … | 2.1790 | 2.9180 | 3.4590 | 4.7550 |
| ω4 | 0.9142 | 2.1970 | 3.8460 | 5.6840 | 7.5500 | 1.8180 | 2.6440 | 4.0720 | 5.8100 | 7.6350 | 2.6560 | 3.1740 | 4.3880 | 6.0050 | 7.7710 |
| ω5 | 0.9170 | 2.8520 | 5.3440 | 7.9550 | 10.590 | 1.8310 | 3.3000 | 5.5170 | 8.0470 | 10.650 | 2.7380 | 3.8370 | 5.7760 | 8.1940 | 10.750 |
| ω6 | 0.9223 | 4.4220 | 6.7440 | 9.4590 | 12.300 | 1.8420 | 4.5390 | 6.8820 | 9.5760 | 12.400 | 2.7530 | 4.7750 | 7.1170 | 9.7700 | 12.560 |
| ω7 | 3.2990 | 4.5390 | 8.9090 | 13.270 | 17.260 | 3.3200 | 4.8180 | 9.0100 | 13.350 | 17.330 | 3.4110 | 5.2210 | 9.1710 | 13.470 | 17.440 |
| ω8 | 4.9960 | 6.2720 | 9.4550 | 13.330 | 17.760 | 5.0040 | 6.3420 | 9.5520 | 13.390 | 17.800 | 5.0240 | 6.4730 | 9.7150 | 13.490 | 17.860 |
| ω9 | 7.3620 | 10.060 | 15.750 | 22.230 | 28.970 | 7.3690 | 10.110 | 15.810 | 22.280 | 29.010 | 7.3820 | 10.200 | 15.900 | 22.360 | 29.080 |

Table 6.8
Natural Frequencies (THz) of a Five-walled CNT With Innermost Radius [24]
| Natural frequencies (THz) | m=1 | m=2 | m=3 | ||||||||||||
| n=0 | n=1 | n=2 | n=3 | n=4 | n=0 | n=1 | n=2 | n=3 | n=4 | n=0 | n=1 | n=2 | n=3 | n=4 | |
| (A) RI=5 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.0309 | 0.0130 | 0.0189 | 0.0332 | … | 0.1005 | 0.0403 | 0.0270 | 0.0354 | … | 0.1807 | 0.0815 | 0.0463 | 0.0424 |
| ω2 | … | 0.3660 | 0.7049 | 1.0310 | 1.0890 | … | 0.4075 | 0.7248 | 1.0190 | 1.0880 | … | 0.4682 | 0.7545 | 1.0130 | 1.0850 |
| ω3 | … | 0.3861 | 0.7450 | 1.0680 | 1.4010 | … | 0.4274 | 0.7668 | 1.0920 | 1.4150 | … | 0.4889 | 0.8005 | 1.1210 | 1.4390 |
| ω4 | … | 0.4086 | 0.7893 | 1.1140 | 1.4790 | … | 0.4497 | 0.8127 | 1.1360 | 1.4910 | … | 0.5087 | 0.8478 | 1.1710 | 1.5130 |
| ω5 | … | 0.4325 | 0.8359 | 1.1770 | 1.5660 | … | 0.4767 | 0.8544 | 1.1920 | 1.5760 | … | 0.5334 | 0.8918 | 1.2160 | 1.5930 |
| ω6 | 0.1695 | 0.4555 | 0.8815 | 1.2520 | 1.6660 | 0.3366 | 0.5152 | 0.8911 | 1.2690 | 1.6770 | 0.4909 | 0.6078 | 0.9181 | 1.2940 | 1.6950 |
| ω7 | 0.1725 | 0.5470 | 0.9314 | 1.3370 | 1.7780 | 0.3448 | 0.6292 | 0.9836 | 1.3540 | 1.7880 | 0.5170 | 0.7395 | 1.0490 | 1.3830 | 1.8050 |
| ω8 | 0.1730 | 0.5925 | 1.1260 | 1.6330 | 1.9950 | 0.3460 | 0.6660 | 1.1650 | 1.6590 | 2.0090 | 0.5190 | 0.7713 | 1.2280 | 1.7010 | 2.0300 |
| ω9 | 0.1732 | 0.6308 | 1.2060 | 1.7600 | 2.2630 | 0.3463 | 0.7003 | 1.2430 | 1.7840 | 2.2800 | 0.5194 | 0.8014 | 1.3020 | 1.8240 | 2.3090 |
| ω10 | 0.1732 | 0.6785 | 1.3080 | 1.8450 | 2.3540 | 0.3464 | 0.7434 | 1.3420 | 1.8640 | 2.3710 | 0.5196 | 0.8394 | 1.3950 | 1.8970 | 2.3980 |
| ω11 | 0.6183 | 0.8813 | 1.3470 | 1.9230 | 2.4870 | 0.6227 | 0.9041 | 1.3690 | 1.9460 | 2.5040 | 0.6404 | 0.9475 | 1.4080 | 1.9830 | 2.5310 |
| ω12 | 1.2960 | 1.3440 | 1.6170 | 2.1590 | 2.6620 | 1.2970 | 1.3470 | 1.6320 | 2.1740 | 2.6750 | 1.2970 | 1.3520 | 1.6570 | 2.1990 | 2.6950 |
| ω13 | 2.2710 | 2.2780 | 2.3090 | 2.4310 | 2.8970 | 2.2710 | 2.2790 | 2.3100 | 2.4360 | 2.9100 | 2.2710 | 2.2790 | 2.3120 | 2.4460 | 2.9300 |
| ω14 | 3.1010 | 3.1040 | 3.1140 | 3.1390 | 3.2160 | 3.1020 | 3.1040 | 3.1140 | 3.1390 | 3.2190 | 3.1020 | 3.1040 | 3.1140 | 3.1400 | 3.2230 |
| ω15 | 3.6410 | 3.6430 | 3.6480 | 3.6600 | 3.6880 | 3.6410 | 3.6430 | 3.6480 | 3.6600 | 3.6880 | 3.6410 | 3.6430 | 3.6480 | 3.6600 | 3.6890 |
| (B) RI=1 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.0773 | 0.1140 | 0.2561 | 0.4299 | … | 0.2456 | 0.1478 | 0.2626 | 0.4332 | … | 0.4466 | 0.2286 | 0.2819 | 0.4410 |
| ω2 | … | 0.7687 | 1.0500 | 1.1740 | 1.3360 | … | 0.7890 | 1.0480 | 1.1740 | 1.3380 | … | 0.8782 | 1.0570 | 1.1770 | 1.3400 |
| ω3 | … | 1.0160 | 1.8550 | 2.0970 | 2.2210 | … | 1.1030 | 1.8390 | 2.0930 | 2.2210 | … | 1.2300 | 1.8440 | 2.0900 | 2.2210 |
| ω4 | … | 1.1490 | 1.9690 | 2.8170 | 2.9890 | … | 1.2790 | 2.0730 | 2.8080 | 2.9870 | … | 1.3800 | 2.1810 | 2.8010 | 2.9840 |
| ω5 | … | 1.2740 | 2.2080 | 2.8790 | 3.4850 | … | 1.3830 | 2.2420 | 2.9420 | 3.4810 | … | 1.6380 | 2.3240 | 3.0380 | 3.4770 |
| ω6 | 0.4571 | 1.4240 | 2.5490 | 3.2860 | 3.7760 | 0.9099 | 1.5910 | 2.6250 | 3.2760 | 3.8210 | 1.3390 | 1.6520 | 2.6780 | 3.2690 | 3.8930 |
| ω7 | 0.4591 | 1.5950 | 2.6580 | 3.3690 | 4.4070 | 0.9165 | 1.6770 | 2.6920 | 3.4410 | 4.4480 | 1.3710 | 1.9490 | 2.7930 | 3.5420 | 4.5120 |
| ω8 | 0.4619 | 1.6750 | 2.9490 | 3.9810 | 5.2940 | 0.9231 | 1.8530 | 3.0140 | 4.0360 | 5.3260 | 1.3820 | 2.1190 | 3.1380 | 4.1220 | 5.3780 |
| ω9 | 0.4637 | 1.9440 | 3.3470 | 4.7650 | 6.1640 | 0.9271 | 2.1190 | 3.4420 | 4.8210 | 6.2110 | 1.3900 | 2.3590 | 3.5770 | 4.9140 | 6.2900 |
| ω10 | 0.4650 | 2.2820 | 3.4690 | 4.9810 | 6.6320 | 0.9298 | 2.3930 | 3.5310 | 5.0200 | 6.6560 | 1.3940 | 2.4980 | 3.6360 | 5.0840 | 6.6980 |
| ω11 | 1.7510 | 2.3390 | 4.2220 | 5.6010 | 7.2110 | 1.7600 | 2.4450 | 4.2600 | 5.6460 | 7.2510 | 1.7950 | 2.6680 | 4.3260 | 5.7220 | 7.3170 |
| ω12 | 2.7210 | 3.2290 | 4.4560 | 6.6660 | 8.6490 | 2.7240 | 3.2520 | 4.5090 | 6.6930 | 8.6830 | 2.7320 | 3.2940 | 4.5930 | 6.7380 | 8.7390 |
| ω13 | 3.4040 | 3.8690 | 4.9250 | 6.6850 | 8.8810 | 3.4060 | 3.8820 | 4.9610 | 6.7250 | 8.8990 | 3.4100 | 3.9060 | 5.0240 | 6.7910 | 8.9300 |
| ω14 | 3.9190 | 4.4070 | 6.0250 | 8.3400 | 10.830 | 3.9200 | 4.4210 | 6.0590 | 8.3720 | 10.850 | 3.9230 | 4.4460 | 6.1170 | 8.4260 | 10.900 |
| ω15 | 4.4320 | 5.2520 | 7.9130 | 11.120 | 14.480 | 4.4340 | 5.2710 | 7.9420 | 11.150 | 14.500 | 4.4360 | 5.3040 | 7.9900 | 11.190 | 14.540 |
| (C) RI=0.5 nm and L/RO=10 | |||||||||||||||
| ω1 | … | 0.1116 | 0.2832 | 0.4961 | 0.6799 | … | 0.3089 | 0.3086 | 0.5023 | 0.6841 | … | 0.5486 | 0.3828 | 0.5212 | 0.6937 |
| ω2 | … | 0.8370 | 1.2290 | 1.6280 | 1.9400 | … | 0.8661 | 1.2300 | 1.6290 | 1.9410 | … | 0.9723 | 1.2430 | 1.6330 | 1.9450 |
| ω3 | … | 1.2520 | 2.0270 | 2.4940 | 2.8730 | … | 1.3170 | 2.0140 | 2.4920 | 2.8740 | … | 1.4390 | 2.0150 | 2.4930 | 2.8750 |
| ω4 | … | 1.4610 | 2.4330 | 3.1350 | 3.4820 | … | 1.5710 | 2.5170 | 3.1280 | 3.4820 | … | 1.6720 | 2.5570 | 3.1230 | 3.4820 |
| ω5 | … | 1.5280 | 2.6650 | 3.5230 | 4.7230 | … | 1.7270 | 2.7000 | 3.5200 | 4.7270 | … | 2.0240 | 2.8540 | 3.5190 | 4.7350 |
| ω6 | 0.5801 | 1.8380 | 2.9610 | 3.6100 | 4.7900 | 1.1540 | 2.0010 | 3.0000 | 3.6960 | 4.8450 | 1.6960 | 2.0640 | 3.0090 | 3.8250 | 4.9330 |
| ω7 | 0.5813 | 1.9640 | 3.1200 | 4.4050 | 5.8540 | 1.1610 | 2.0940 | 3.2260 | 4.4780 | 5.9000 | 1.7390 | 2.4480 | 3.4150 | 4.5930 | 5.9740 |
| ω8 | 0.5836 | 2.1930 | 3.8020 | 5.6590 | 7.5330 | 1.1660 | 2.4020 | 3.9170 | 5.7130 | 7.5680 | 1.7450 | 2.7260 | 4.0850 | 5.8000 | 7.6250 |
| ω9 | 0.5862 | 2.7330 | 4.3390 | 6.0210 | 7.8110 | 1.1710 | 2.9560 | 4.4200 | 6.0930 | 7.8720 | 1.7540 | 3.1220 | 4.5600 | 6.2150 | 7.9720 |
| ω10 | 0.5886 | 2.9170 | 5.3080 | 7.3770 | 9.5580 | 1.1770 | 2.9860 | 5.3800 | 7.4360 | 9.6070 | 1.7630 | 3.2500 | 5.4950 | 7.5330 | 9.6900 |
| ω11 | 2.1850 | 3.9630 | 5.3750 | 7.9370 | 10.570 | 2.1970 | 3.9920 | 5.4340 | 7.9740 | 10.600 | 2.2440 | 4.0490 | 5.5370 | 8.0360 | 10.640 |
| ω12 | 3.3690 | 4.4790 | 6.7950 | 9.4600 | 12.290 | 3.3740 | 4.5980 | 6.8460 | 9.5060 | 12.330 | 3.3830 | 4.7840 | 6.9320 | 9.5830 | 12.390 |
| ω13 | 4.1580 | 4.7800 | 8.8890 | 13.250 | 17.250 | 4.1600 | 4.8060 | 8.9300 | 13.280 | 17.270 | 4.1660 | 4.8530 | 8.9970 | 13.340 | 17.320 |
| ω14 | 5.0370 | 6.2600 | 9.4350 | 13.320 | 17.760 | 5.0400 | 6.2870 | 9.4740 | 13.340 | 17.770 | 5.0450 | 6.3340 | 9.5380 | 13.380 | 17.790 |
| ω15 | 7.3600 | 10.050 | 15.7300 | 22.220 | 28.960 | 7.3630 | 10.070 | 15.760 | 22.240 | 28.980 | 7.3670 | 10.110 | 15.800 | 22.270 | 29.000 |

Wang et al. [32] stated that the effect of vdW interaction is less pronounced for radial modes of small-radius MWCNTs due to the fact that the interlayer vdW interaction is characterized by a radius-independent vdW interaction coefficient. In contrast, our more refined model for the interlayer vdW interaction is characterized by a radius-dependent vdW interaction coefficient and the results for the natural frequencies did show that the effect of vdW interaction on the radial modes of small-radius MWCNTs is significant. Figs. 6.9 and 6.10 show the influence of vdW interaction on the natural frequencies of a DWCNT with small innermost radius RI=0.65 nm. Indeed, the effect of the vdW interaction on the frequencies which are associated with the torsional and longitudinal vibrations is very small and can be neglected. However, for the lower mode-order vibration such as m=1 and n<5 or n=1 and m<10, frequencies associated with the radial vibration when considering the vdW interaction are significantly different from those when ignoring the vdW interaction, indicating again that vdW interaction does play an important role in the radial vibration of the small-radius DWCNT.
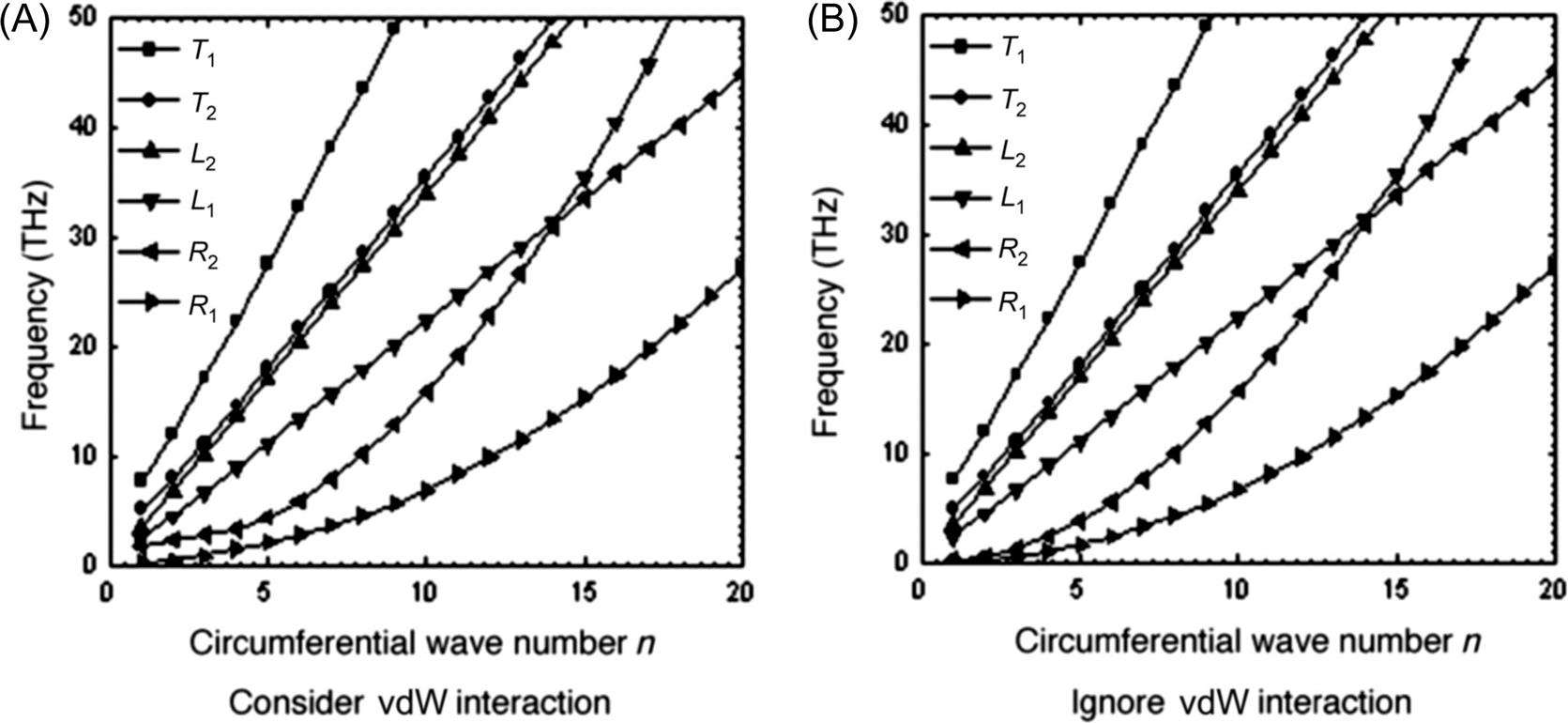

To show the effect of the innermost radius on the lower mode-order frequencies of a DWCNT, frequencies associated with the radial vibration are calculated from Eqs. (6.55) and (6.56) and presented in Fig. 6.11 for the breathing vibration (m=1, n=0). The frequencies associated with the torsional, longitudinal, and radial vibrations (m=1, n=1) are calculated from Eq. (6.46) and presented in Fig. 6.12. It is observed from Figs. 6.11 and 6.12 that the frequencies are the function of the tube radius. With a small radius, say, less than 5 nm, the frequencies drop rapidly, indicating that the radius effect plays an important role in the frequencies of a small-radius MWCNT. For a DWCNT with a large radius, say, greater than 10 nm, the frequencies vary very slowly, showing that the dependence of the frequencies on the radius can be neglected when the tube radius is large enough. Also, the higher frequency associated with the radial vibration is almost a constant and independent of the tube radius when the innermost radius is greater than 10 nm, indicating again that the vdW interaction plays a critical role on the higher radial vibration of MWCNTs. Also, it is clear from Figs. 6.3 and 6.4 that the interlayer vdW interaction plays a critical role on the higher frequency associated with radial vibration of an MWCNT with arbitrary radius, but the effect of vdW interaction on the lower frequency associated with the radial vibration and on the frequencies associated with the torsional and the longitudinal vibrations is very small and is negligible for MWCNTs with radii from very small to very large.

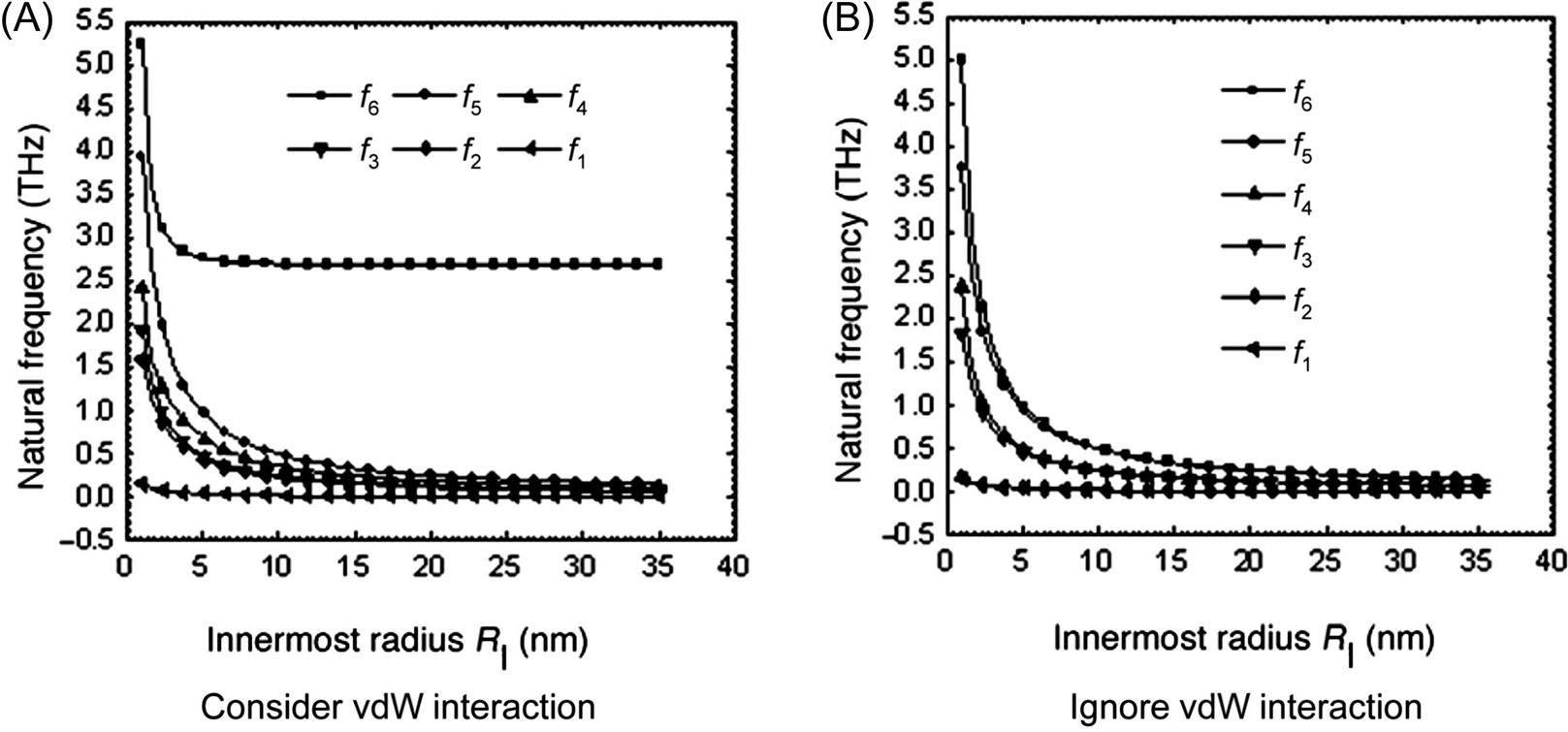
The effect of the innermost radius on the higher mode order (m=5, n=5) frequencies of a DWCNT is shown in Fig. 6.13 for various innermost radii. When the interlayer vdW interaction is ignored, the mode shapes associated with f1–f6 do not change for different tube radii, as shown in Fig. 6.13B. However, when the vdW interaction is considered, the mode shapes which are associated with some frequencies will change from radial, torsional, and longitudinal mode shapes to other shapes as the innermost radius is varied from small to large radii. For example, in Fig. 6.13A, as the innermost radius increases, the mode shape associated with the frequency f6 changes from torsional mode (RI<7 nm) to a mix of radial and torsional modes (7 nm≤RI≤9 nm), and then to a radial mode (RI≥9 nm), and the mode shape associated with frequency f4 changes from longitudinal mode (RI≤4 nm) to a mix of longitudinal and torsional modes (4 nm≤RI≤8 nm), and then to a torsional mode (RI>8 nm). Similarly, the mode shape associated with frequency f2 changes from radial mode (RI≤2 nm) to a mix of radial and longitudinal modes (2 nm≤RI≤4 nm), and then to a longitudinal mode (RI≤4 nm). In contrast, the mode shapes associated with the frequencies f3 and f1 do not change for different tube radii.
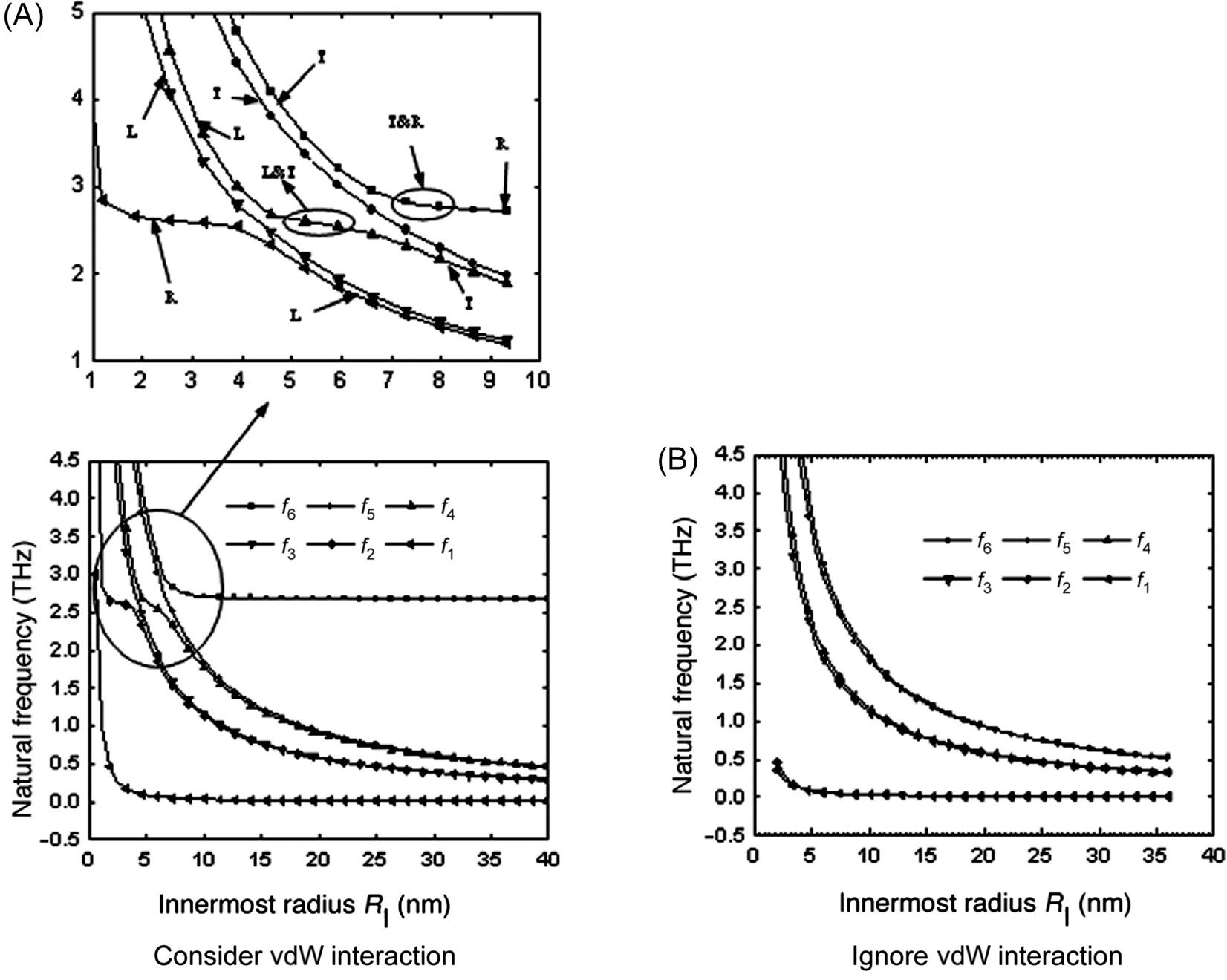
As the radius of a tube in an MWCNT is increased the stiffening effect of that particular tube on the entire MWCNT assembly is reduced, and therefore a different physical combination among all the factors is obtained. This is similar to the vibrations of beams on elastic foundations, where the mode number is increased as the stiffness of the elastic foundation is increased. In the current problem, on top of this, also the coupling in the displacement field makes it more complex, and one can see in Fig. 6.13 the continuous change in the modal composition when the vdW interaction is considered.
In summary, based on the more refined vdW interaction formulas, the free vibration of an MWCNT is investigated by using the Donnell shell model. In contrast to the work by Wang et al. [32] where they conclude that the effect of the vdW interaction is less significant for the radial vibration of small-radius MWCNTs, our numerical results reveal that the effect of the vdW interaction plays a significant role on the higher natural frequencies which are associated with radial vibration of small-radius MWCNTs. This is due to the fact that our continuum model is based on radius-dependent vdW interaction formulas, as compared to the radius-independent vdW interaction formulas that were used by Wang et al. [32] The effects of the tube radius and the interlayer vdW interaction are also examined on the mode shapes of MWCNTs. When ignoring the vdW interaction, the mode shapes of MWCNTs do not change as the radii of the MWCNTs are varied from very small to very large. However, when the vdW interaction is considered, it is observed that some of the mode shapes will change between radial, torsional, and longitudinal modes, due to the effect of the vdW interaction even for cases where the innermost radius is less than 2 nm, indicating again that the interlayer vdW interaction plays a significant role in the vibration of MWCNTs with small radius. In addition, the numerical simulations show that ultrahigh natural frequency can be achieved by using an MWCNT. For a given combination of m and n, the lowest natural frequencies are not influenced by the vdW interaction. However, other higher natural frequencies are significantly dependent on the vdW interaction. Especially, the vdW interaction plays a dominant role on the higher radial frequencies so that the effect of the mode order can be neglected.
