Equations wherein the unknown quantity is a function, rather than a variable, and that involve derivatives of the unknown function, are known as differential equations. An ordinary differential equation is the special case where the unknown function has only one independent variable with respect to which derivatives occur in the equation. If, on the other hand, derivatives of more than one variable occur in the equation, then it is known as a partial differential equation, and that is the topic of Chapter 11. Here we focus on ordinary differential equations (in the following abbreviated as ODEs), and we explore both symbolic and numerical methods for solving this type of equations in this chapter. Analytical closed-form solutions to ODEs often do not exist, but for many special types of ODEs there are analytical solutions, and in those cases there is a chance that we can find solutions using symbolic methods. If that fails, we must, as usual, resort to numerical techniques.

Ordinary differential equations are ubiquitous in science and engineering, as well as in many other fields, and they arise, for example, in studies of dynamical systems. A typical example of an ODE is an equation that describes the time evolution of a process where the rate of change (the derivative) can be related to other properties of the process. To learn how the process evolves in time, given some initial state, we must solve, or integrate, the ODE that describes the process. Specific examples of applications of ODEs are the laws of mechanical motion in physics, molecular reactions in chemistry and biology, and population modeling in ecology, just to mention a few.

In this chapter we will explore both symbolic and numerical approaches to solving ODE problems. For symbolic methods we use the SymPy module, and for numerical integration of ODEs we use functions from the integrate module in SciPy.

Importing Modules

Here we require the NumPy and Matplotlib libraries for basic numerical and plotting purposes, and for solving ODEs we need the SymPy library and SciPy’s integrate module. As usual, we assume that these modules are imported in the following manner:

In [1]: import numpy as np
In [2]: import matplotlib.pyplot as plt
In [3]: from scipy import integrate
In [4]: import sympy

For nicely displayed output from SymPy we need to initialize its printing system:

In [5]: sympy.init_printing()

Ordinary Differential Equations

The simplest form of an ordinary differential equation is where y(x) is the unknown function and ) is known. It is a differential equation because the derivative of the y(x) occurs in the equation. Only the first derivative occurs in the equation, and it is therefore an example of a first-order ODE. More generally, we can write an ODE of nth order in explicit form as , or in implicit form as , where f and F are known functions.

An example of a first-order ODE is Newton’s law of cooling which describes the temperature T(t) of a body in a surrounding with temperature T_a. The solution to this ODE is where T₀ is the initial temperature of the body. An example of a second-order ODE is Newton’s second law of motion or more explicitly This equation describes the position x(t) of an object with mass m, when subjected to a position-dependent force F(x(t)). To completely specify a solution to this ODE we would, in addition to finding its general solution, also have to give the initial position and velocity of the object. Similarly, the general solution of an nth order ODE have n free parameters that we need to specify, for example, as initial conditions for the unknown function and of its derivatives.

An ODE can always be rewritten as a system of first-order ODEs. Specifically, the nth order ODE on the explicit form , can be written in the standard form by introducing n new functions , , ..., . This gives the following system of first-order ODEs:

which also can be written in a more compact vector form: This canonical form is particularly useful for numerical solutions of ODEs, and it is common that numerical methods for solving ODEs takes the function which in the current case is as the input that specifies the ODE. For example, the second-order ODE for Newton’s second law of motion, can be written on the standard form using , giving

If the functions f₁, f₂, ..., f_n are all linear, then the corresponding system of ODEs can be written on the simple form where A(x) is an matrix, and r(x) is an n-vector, that only depend on x. In this form, the r(x) is known as the source term, and the linear system is known as homogeneous if , and nonhomogeneous otherwise. Linear ODEs are an important special case that can be solved, for example, using eigenvalue decomposition of A(x). Likewise, for certain properties and forms of the function f(x, y(x)), there may be known solutions and special methods for solving the corresponding ODE problem, but there is no general method for an arbitrary f(x, y(x)), other than approximate numerical methods.

In addition to the properties of the function f(x, y(x)), the boundary conditions for an ODE also influence the solvability of the ODE problem, as well as which numerical approaches are available. Boundary conditions are needed to determine the values of the integration constants that appear in a solution. There are two main types of boundary conditions for ODE problems: initial value conditions and boundary value conditions. For initial value problems, the value of the function and its derivatives are given at a starting point, and the problem is to evolve the function forward in the independent variable (for example, representing time or position) from this starting point. For boundary value problems, the value of the unknown function, or its derivatives, are given at fixed points. These fixed points are frequently the endpoints of the domain of interest. In this chapter we mostly focus on initial value problem, and methods that are applicable to boundary value problems are discussed in Chapter 11 on partial differential equations.

Symbolic Solution to ODEs

SymPy provides a generic ODE solver sympy.dsolve, which is able to find analytical solutions to many elementary ODEs. The sympy.dsolve function attempts to automatically classify a given ODE, and it may attempt a variety of techniques to find its solution. It is also possible to give hints to the dsolve function, which can guide it to the most appropriate solution method. While dsolve can be used to solve many simple ODEs symbolically, as we will see in the following, it is worth keeping in mind that most ODEs cannot be solved analytically. Typical examples of ODEs where one can hope to find a symbolic solution are ODEs of first or second-order, or linear systems of first-order ODEs with only a few unknown functions. It also helps greatly if the ODE has special symmetries or properties, such as being separable, having constant coefficients, or is on a special form for which there exist known analytical solutions. While these types of ODEs are exceptions and special cases, there are many important applications of such ODEs, and for these cases SymPy’s dsolve can be a very useful complement to traditional analytical methods. In this section we will explore how to use SymPy and its dsolve function to solve simple but commonly occurring ODEs.

To illustrate the method for solving ODEs with SymPy, we begin with the simplest possible problem and gradually look at more complicated situations. The first example is the simple first-order ODE for Newton’s cooling law, with the initial value To approach this problem using SymPy, we first need to define symbols for the variables t, k, T₀ and T_a, and to represent the unknown function T(t) we can use a sympy.Function object:

In [6]: t, k, T0, Ta = sympy.symbols("t, k, T_0, T_a")
In [7]: T = sympy.Function("T")

Next, we can define the ODE very naturally by simply creating a SymPy expression for the left-hand side of the ODE when written on the form . Here, to represent the function T(t) we can now use the Sympy Function object T. Applying the symbol t to it, using the function-call syntax T(t), results in an applied function object that we can take derivatives of using either sympy.diff or the diff method on the T(t) expression:

In [8]: ode = T(t).diff(t) + k*(T(t) - Ta)
In [9]: sympy.Eq(ode)
Out[9]:  

Here we used sympy.Eq to display the equation including the equality sign and a right-hand side that is zero. Given this representation of the ODE, we can directly pass it to sympy.dsolve, which will attempt to automatically find the general solution of the ODE.

In [10]: ode_sol = sympy.dsolve(ode)
In [11]: ode_sol
Out[11]:  

For this ODE problem, the sympy.dsolve function indeed finds the general solution, which here includes an unknown integration constant C₁ that we have to determine from the initial conditions for the problem. The return value from the sympy.dsolve is an instance of sympy.Eq, which is a symbolic representation of an equality. It has the attributes lhs and rhs for accessing the left-hand side and the right-hand side of the equality object:

In [12]: ode_sol.lhs
Out[12]: T (t)
In [13]: ode_sol.rhs
Out[13]:  

Once the general solution has been found, we need to use the initial conditions to find the values of the yet-to-be-determined integration constants. Here the initial condition is To this end, we first create a dictionary that describes the initial condition, ics = {T(0): T0}, which we can use with SymPy’s subs method to apply the initial condition to the solution of the ODE. This results in an equation for the unknown integration constant C₁:

In [14]: ics = {T(0): T0}
In [15]: ics
Out[15]: {T (0):T0}
In [16]: C_eq = sympy.Eq(ode_sol.lhs.subs(t, 0).subs(ics), ode_sol.rhs.subs(t, 0))
In [17]: C_eq
Out[17]:  

In the present example, the equation for C₁ is trivial to solve, but for the sake of generality, here we solve it using sympy.solve. The result is a list of solutions (in this case a list of only one solution). We can substitute the solution for C₁ into the general solution of the ODE problem to obtain the particular solution that corresponds to the given initial conditions:

In [18]: C_sol = sympy.solve(C_eq)
In [19]: C_sol
Out[19]:  
In [20]: ode_sol.subs(C_sol[0])
Out[20]:  

By carrying out these steps we have completely solved the ODE problem symbolically, and we obtained the solution The steps involved in this process are straightforward, but applying the initial conditions and solving for the undetermined integration constants can be slightly tedious, and it worthwhile to collect these steps in a reusable function. The following function apply_ics is a basic implementation that generalizes these steps to a differential equation of arbitrary order.

In [21]: def apply_ics(sol, ics, x, known_params):
   ....:      """
   ....:      Apply the initial conditions (ics), given as a dictionary on
   ....:      the form ics = {y(0): y0, y(x).diff(x).subs(x, 0): yp0, ...},
   ....:      to the solution of the ODE with independent variable x.
   ....:      The undetermined integration constants C1, C2, ... are extracted
   ....:      from the free symbols of the ODE solution, excluding symbols in
   ....:      the known_params list.
   ....:      """
   ....:      free_params = sol.free_symbols - set(known_params)
   ....:      eqs = [(sol.lhs.diff(x, n) - sol.rhs.diff(x, n)).subs(x, 0).subs(ics)
   ....:             for n in range(len(ics))]
   ....:      sol_params = sympy.solve(eqs, free_params)
   ....:      return sol.subs(sol_params)

With this function, we can more conveniently single out a particular solution to an ODE that satisfies a set of initial conditions, given the general solution to the same ODE. For our previous example we get:

In [22]: ode_sol
Out[22]:  
In [23]: apply_ics(ode_sol, ics, t, [k, Ta])
Out[23]:  

The example we looked at so far is almost trivial, but the same method can be used to approach any ODE problem, although here is of course no guarantee that a solution will be found. As an example of a slightly more complicated problem, consider the ODE for a damped harmonic oscillator, which is a second-order ODE on the form , where x(t) is the position of the oscillator at time t, ω₀ is the frequency for the undamped case, and γ  is the damping ratio. We first define the required symbols and construct the ODE, and then ask SymPy to find the general solution by calling sympy.dsolve:

In [24]: t, omega0, gamma= sympy.symbols("t, omega_0, gamma", positive=True)
In [25]: x = sympy.Function("x")
In [26]: ode = x(t).diff(t, 2) + 2 * gamma * omega0 * x(t).diff(t) + omega0**2 * x(t)
In [27]: sympy.Eq(ode)
Out[27]:  
In [28]: ode_sol = sympy.dsolve(ode)
In [29]: ode_sol
Out[29]:  

Since this is a second-order ODE, there are two undetermined integration constants in the general solution. We need to specify initial conditions for both the position x(0) and the velocity to single out a particular solution to the ODE. To do this we create a dictionary with these initial conditions and apply it to the general ODE solution using apply_ics:

In [30]: ics = {x(0): 1, x(t).diff(t).subs(t, 0): 0}
In [31]: ics
Out[31]: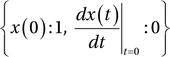  
In [32]: x_t_sol = apply_ics(ode_sol, ics, t, [omega0, gamma])
In [33]: x_t_sol
Out[33]:  

This is the solution for the dynamics of the oscillator for arbitrary values of t, ω₀ and γ, where we used the initial condition and However, substituting which corresponds to critical damping, directly into this expression results in a division by zero error, and for this particular choice of γ  we need to careful and compute the limit where

In [34]: x_t_critical = sympy.limit(x_t_sol.rhs, gamma, 1)
In [35]: x_t_critical
Out[35]:  

Finally, we plot the solutions for and a sequence of different values of the damping ratio γ :

In [36]: fig, ax = plt.subplots(figsize=(8, 4))
    ...: tt = np.linspace(0, 3, 250)
    ...: w0 = 2 * sympy.pi
    ...: for g in [0.1, 0.5, 1, 2.0, 5.0]:
    ...:     if g == 1:
    ...:         x_t = sympy.lambdify(t, x_t_critical.subs({omega0: w0}), 'numpy')
    ...:     else:
    ...:         x_t = sympy.lambdify(t, x_t_sol.rhs.subs({omega0: w0, gamma: g}), 'numpy')
    ...:     ax.plot(tt, x_t(tt).real, label=r"$gamma = %.1f$" % g)
    ...: ax.set_xlabel(r"$t$", fontsize=18)
    ...: ax.set_ylabel(r"$x(t)$", fontsize=18)
    ...: ax.legend()

The solution to the ODE for the damped harmonic oscillator is graphed in Figure 9-1. For the oscillator is underdamped, and we see oscillatory solutions. For the oscillator is overdamped, and decays monotonically. The crossover between these two behaviors occurs at the critical damping ratio

The two examples of ODEs we have looked at so far could both be solved exactly by analytical means, but this is far from always the case. Even many first-order ODEs cannot be solved exactly in terms of elementary functions. For example, consider which is an example of an ODE that does not have any closed-form solution. If we try to solve this equation using sympy.dsolve we obtain an approximate solution, in the form of a power series:

In [37]: x = sympy.symbols("x")
In [38]: y = sympy.Function("y")
In [39]: f = y(x)**2 + x
In [40]: sympy.Eq(y(x).diff(x), f)
Out[40]:  
In [41]: sympy.dsolve(y(x).diff(x) - f)
Out[41]:  

For many other types of equations, SymPy outright fails to produce any solution at all. For example, if we attempt to solve the second-order ODE we obtain the following error message:

In [42]: sympy.Eq(y(x).diff(x, x), f)
Out[42]:  
In [43]: sympy.dsolve(y(x).diff(x, x) - f)
---------------------------------------------------------------------------
...
NotImplementedError: solve: Cannot solve -x - y(x)**2 + Derivative(y(x), x, x)

This type of result can mean that there actually is no analytic solution to the ODE, or, just as likely, simply that SymPy is unable to handle it.

The dsolve function accepts many optional arguments, and it can frequently make a difference if the solver is guided by giving hints about which methods should be used to solve the ODE problem at hand. See the docstring for sympy.dsolve for more information about the available options.

Direction Fields

A direction field graph is a simple but useful technique to visualize possible solutions to arbitrary first-order ODEs. It is made up of short lines that show the slope of the unknown function on a grid in the x–y plane. This graph can be easily produced because the slope of y(x) at arbitrary points of the x–y plane is given by the definition of the ODE: That is, we only need to iterate over the x and y values on the coordinate grid of interest and evaluate f(x, y(x)) to know the slope of y (x) at that point. The reason why the direction field graph is useful is that smooth and continuous curves that tangent the slope lines (at every point) in the direction field graph are possible solutions to the ODE.

The following function plot_direction_field produces a direction field graph for a first-order ODE, given the independent variable x, the unknown function y(x) and the right-hand side function f(x, y (x)). It also takes optional ranges for the x and y axes (x_lim and y_lim, respectively) and an optional Matplotlib axis instance to draw the graph on.

 In [44]: def plot_direction_field(x, y_x, f_xy, x_lim=(-5, 5), y_lim=(-5, 5), ax=None):
    ...:     f_np = sympy.lambdify((x, y_x), f_xy, 'numpy')
    ...:     x_vec = np.linspace(x_lim[0], x_lim[1], 20)
    ...:     y_vec = np.linspace(y_lim[0], y_lim[1], 20)
    ...:
    ...:     if ax is None:
    ...:         _, ax = plt.subplots(figsize=(4, 4))
    ...:
    ...:     dx = x_vec[1] - x_vec[0]
    ...:     dy = y_vec[1] - y_vec[0]
    ...:
    ...:     for m, xx in enumerate(x_vec):
    ...:         for n, yy in enumerate(y_vec):
    ...:             Dy = f_np(xx, yy) * dx
    ...:             Dx = 0.8 * dx**2 / np.sqrt(dx**2 + Dy**2)
    ...:             Dy = 0.8 * Dy*dy / np.sqrt(dx**2 + Dy**2)
    ...:             ax.plot([xx - Dx/2, xx + Dx/2],
    ...:                     [yy - Dy/2, yy + Dy/2], 'b', lw=0.5)
    ...:     ax.axis('tight')
    ...:     ax.set_title(r"$%s$" %
    ...:                  (sympy.latex(sympy.Eq(y(x).diff(x), f_xy))),
    ...:                  fontsize=18)
    ...:     return ax

With this function we can produce the direction field graphs for the ODEs on the form For example, the following code generates the direction field graphs for and The result is shown in Figure 9-2.

In [45]: x = sympy.symbols("x")
In [46]: y = sympy.Function("y")
In [47]: fig, axes = plt.subplots(1, 3, figsize=(12, 4))
    ...: plot_direction_field(x, y(x), y(x)**2 + x, ax=axes[0])
    ...: plot_direction_field(x, y(x), -x / y(x), ax=axes[1])
    ...: plot_direction_field(x, y(x), y(x)**2 / x, ax=axes[2])

The direction lines in the graphs in Figure 9-2 suggest how the curves that are solutions to the corresponding ODE behave, and direction field graphs are therefore a useful and tool for visualizing solutions to ODEs that cannot be solved analytically. To illustrate this point, consider again the ODE with the initial condition which we previously saw can be solved inexactly as an approximate power series. Like before, we solve this problem again by defining the symbol x and the function y(x), which we in turn use to construct and display the ODE:

In [48]: x = sympy.symbols("x")
In [49]: y = sympy.Function("y")
In [50]: f = y(x)**2 + x
In [51]: sympy.Eq(y(x).diff(x), f)
Out[51]:  

Now we want to find the specific power-series solution that satisfy the initial condition, and for this problem we can specify the initial condition directly using the ics keyword argument to the dsolve function¹:

In [52]: ics = {y(0): 0}
In [53]: ode_sol = sympy.dsolve(y(x).diff(x) - f, ics=ics)
In [54]: ode_sol
Out[54]:  

Plotting the solution together with the direction field for the ODE is a quick and simple way to get an idea of the validity range of the power-series approximation. The following code plots the approximate solution and the direction field (Figure 9-3, left panel). A solution with extended validity range is also obtained by repeatedly solving the ODE with initial conditions at increasing values of x, taken from a previous power-series solution (Figure 9-3, right panel).

In [55]: fig, axes = plt.subplots(1, 2, figsize=(8, 4))
    ...: # left panel
    ...: plot_direction_field(x, y(x), f, ax=axes[0])
    ...: x_vec = np.linspace(-3, 3, 100)
    ...: axes[0].plot(x_vec, sympy.lambdify(x, ode_sol.rhs.removeO())(x_vec), 'b', lw=2)
    ...: axes[0].set_ylim(-5, 5)
    ...:
    ...: # right panel
    ...: plot_direction_field(x, y(x), f, ax=axes[1])
    ...: x_vec = np.linspace(-1, 1, 100)
    ...: axes[1].plot(x_vec, sympy.lambdify(x, ode_sol.rhs.removeO())(x_vec), 'b', lw=2)
    ...: # iteratively resolve the ODE with updated initial conditions
    ...: ode_sol_m = ode_sol_p = ode_sol
    ...: dx = 0.125
    ...: # positive x
    ...: for x0 in np.arange(1, 2., dx):
    ...:     x_vec = np.linspace(x0, x0 + dx, 100)
    ...:     ics = {y(x0): ode_sol_p.rhs.removeO().subs(x, x0)}
    ...:     ode_sol_p = sympy.dsolve(y(x).diff(x) - f, ics=ics, n=6)
    ...:     axes[1].plot(x_vec, sympy.lambdify(x, ode_sol_p.rhs.removeO())(x_vec), 'r', lw=2)
    ...: # negative x
    ...: for x0 in np.arange(1, 5, dx):
    ...:     x_vec = np.linspace(-x0-dx, -x0, 100)
    ...:     ics = {y(-x0): ode_sol_m.rhs.removeO().subs(x, -x0)}
    ...:     ode_sol_m = sympy.dsolve(y(x).diff(x) - f, ics=ics, n=6)
    ...:     axes[1].plot(x_vec, sympy.lambdify(x, ode_sol_m.rhs.removeO())(x_vec), 'r', lw=2)

In the left panel of Figure 9-3, we see that the approximate solution curve aligns well with the direction field lines near but starts to deviate for , suggesting that the approximate solution is no longer valid. The solution curve shown in the right panel aligns better with the direction field throughout the plotted range. The blue curve segment is the original approximate solution, and the red curves are continuations obtained from resolving the ODE with an initial condition sequence that starts where the blue curves end.

Solving ODEs using Laplace Transformations

An alternative to solving ODEs symbolically with SymPy’s “black-box” solver² dsolve, is to use the symbolic capabilities of SymPy to assist in a more manual approach to solving ODEs. A technique that can be used to solve certain ODE problems is to Laplace transform the ODE, which for many problems results in an algebraic equation that is easier to solve. The solution to the algebraic equation can then be transformed back to the original domain with an inverse Laplace transform, to obtain the solution to the original problem. The key to this method is that the Laplace transform of the derivative of a function is an algebraic expression in the Laplace transform of the function itself: However, while SymPy is good at Laplace transforming many types of elementary functions, it does not recognize how to transform derivatives of an unknown function. But defining a function that performs this task easily amends this shortcoming.

For example, consider the following differential equation for a driven harmonic oscillator:

To work with this ODE we first create SymPy symbols for the independent variable t and the function y(t), and then use them to construct the symbolic expression for the ODE:

In [56]: t = sympy.symbols("t", positive=True)
In [57]: y = sympy.Function("y")
In [58]: ode = y(t).diff(t, 2) + 2 * y(t).diff(t) + 10 * y(t) - 2 * sympy.sin(3*t)
In [59]: sympy.Eq(ode)
Out[59]:  

Laplace transforming this ODE should yield an algebraic equation. To pursue this approach using SymPy and its function sympy.laplace_transform, we first need to create a symbol s, to be used in the Laplace transformation. At this point we also create a symbol Y for later use.

In [60]: s, Y = sympy.symbols("s, Y", real=True)

Next we proceed to Laplace transforming the unknown function y(t), as well as the entire ODE equation:

In [61]: L_y = sympy.laplace_transform(y(t), t, s)
In [62]: L_y
Out[62]: Lt [ y (t)](s)
In [63]: L_ode = sympy.laplace_transform(ode, t, s, noconds=True)
In [64]: sympy.Eq(L_ode)
Out[64]:  

When Laplace transforming the unknown function y(t) we get the undetermined result , which is to be expected. However, applying sympy.laplace_transform on a derivative of y(t), such as results in the unevaluated expression, This is not the desired result, and we need to work around this issue to obtain the sought-after algebraic equation. The Laplace transformation if the derivative of an unknown function has a well-known form that involves the Laplace transform of the function itself, rather than its derivatives. For the nth derivative of a function y(t), the formula is

By iterating through the SymPy expression tree for L_ode, and replacing the occurrences of with expressions of the form given by this formula, we can obtain the algebraic form of the ODE that we seek. The following functions takes a Laplace-transformed ODE and performs the substitution of the unevaluated Laplace transforms of the derivatives of y(t):

In [65]: def laplace_transform_derivatives(e):
    ...:     """
    ...:     Evaluate the unevaluted laplace transforms of derivatives
    ...:     of functions
    ...:     """
    ...:     if isinstance(e, sympy.LaplaceTransform):
    ...:         if isinstance(e.args[0], sympy.Derivative):
    ...:             d, t, s = e.args
    ...:             n = len(d.args) - 1
    ...:             return ((s**n) * sympy.LaplaceTransform(d.args[0], t, s) -
    ...:                     sum([s**(n-i) * sympy.diff(d.args[0], t, i-1).subs(t, 0)
    ...:                          for i in range(1, n+1)]))
    ...:
    ...:     if isinstance(e, (sympy.Add, sympy.Mul)):
    ...:         t = type(e)
    ...:         return t(*[laplace_transform_derivatives(arg) for arg in e.args])
    ...:
    ...:     return e

Applying this function on the Laplace-transformed ODE equation, L_ode, yields:

In [66]: L_ode_2 = laplace_transform_derivatives(L_ode)
In [67]: sympy.Eq(L_ode_2)
Out[67]: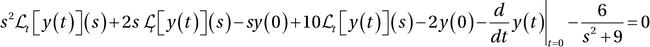  

To simplify the notation, we now substitute the expression L_t[y(t)](s) for the symbol Y:

In [68]: L_ode_3 = L_ode_2.subs(L_y, Y)
In [69]: sympy.Eq(L_ode_3)
Out[69]:  

At this point we need to specify the boundary conditions for the ODE problem. Here we use and and after creating dictionary that contains these boundary conditions, we use it to substitute the values into the Laplace-transformed ODE equation:

In [70]: ics = {y(0): 1, y(t).diff(t).subs(t, 0): 0}
In [71]: ics
Out[71]:  
In [72]: L_ode_4 = L_ode_3.subs(ics)
In [73]: sympy.Eq(L_ode_4)
Out[74]:  

This is an algebraic equation that can be solved for Y:

In [75]: Y_sol = sympy.solve(L_ode_4, Y)
In [76]: Y_sol
Out[76]:  

The result is a list of solutions, which in this case contains only one element. Performing the inverse Laplace transformation on this expression gives the solution to the original problem in the time domain:

In [77]: y_sol = sympy.inverse_laplace_transform(Y_sol[0], s, t)
In [78]: sympy.simplify(y_sol)
Out[78]:  

This technique of Laplace transforming an ODE, solving the corresponding algebraic equation, and inverse Laplace transforming the result to obtain the solution to the original problem, can be applied to solve many practically important ODE problems that arise in, for example, electrical engineering and process control applications. Although these problems can be solved by hand with the help of Laplace transformation tables, using SymPy has the potential of significantly simplifying the process.

Numerical Methods for Solving ODEs

While some ODE problems can be solved with analytical methods, as we have seen examples of in the previous sections, it is much more common with ODE problems that cannot be solved analytically. In practice, ODE problems are therefore mainly solved with numerical methods. There are many approaches to solving ODEs numerically, and most of them are designed for problems that are formulated as a system of first-order ODEs on the standard form³ where y(x) is a vector of unknown functions of x. SciPy provides functions for solving this kind of problems, but before we explore how to use those functions we briefly review the fundamental concepts and introduce the terminology used for numerical integration of ODE problems.

The basic idea of many numerical methods for ODEs is captured in Euler’s method. This method can, for example, be derived from a Taylor-series expansion of y(x) around the point x:

where for notational simplicity we consider the case when y(x) is a scalar function. By dropping terms of second order or higher we get the approximate equation which is accurate to first order in the stepsize h. This equation can be turned into an iteration formula by discretizing the x variable, x₀, x₁, ..., x_k, choosing the stepsize and denoting The resulting iteration formula is known as the forward Euler method, and it is said to be an explicit form because given the value of the y_k we can directly compute using the formula. The goal of the numerical solution of an initial value problem is to compute at some points x_n, given the initial condition An iteration formula like the forward Euler method can therefore be used to compute successive values of y_k, starting from y₀. There are two types of errors involved in this approach: First, the truncation of the Taylor series gives error that limits the accuracy of the method. Second, using the approximation of y_k given by the previous iteration when computing gives an additional error that may accumulate over successive iterations, and that can affect the stability of the method.

An alternative form, which can be derived in a similar manner, is the backward Euler method, given by the iteration formula . This is an example of a backward differentiation formula (BDF), which is implicit, because occurs on both sides of the equation. To compute we therefore need to solve an algebraic equation (for example using Newton’s method, see Chapter 5). Implicit methods are more complicated to implement than explicit methods, and each iteration requires more computational work. However, the advantage is that implicit methods generally have larger stability region and better accuracy, which means that larger stepsize h_k can be used while still obtaining an accurate and stable solution. Whether explicit or implicit methods are more efficient depends on the particular problem that is being solved. Implicit methods are often particularly useful for stiff problems, which loosely speaking are ODE problems that describe dynamics with multiple disparate time scales (for example, dynamics that includes both fast and slow oscillations).

There are several methods to improve upon the first-order Euler forward and backward methods. One strategy is to keep higher-order terms in the Taylor-series expansion of , which gives higher-order iteration formulas that can have better accuracy, such as the second-order method . However, such methods require evaluating higher-order derivatives of y(x), which may be a problem if f (x, y(x)) is not known in advance (and not given in symbolic form). Ways around this problem include to approximate the higher-order derivatives using finite-difference approximations of the derivatives, or by sampling the function f (x, y(x)) at intermediary points in the interval . An example of this type of method is the well-known Runge-Kutta method, which is a single-step method that uses additional evaluations of f (x, y(x)). The most well-known Runge-Kutta method is the 4th-order scheme:

where

Here, k₁ to k₄ are four different evaluations of the ODE function f(x, y(x)) that are used in the explicit formula for given above. The resulting estimate of is accurate to 4th order, with an error of 5th order. Higher-order schemes that use more function evaluations can also be constructed. By combining two methods of different order, it can be possible to also estimate the error in the approximation. A popular combination is the Runge-Kutta 4th and 5th order schemes, which results in a 4th-order accurate method with error estimates. It is known as RK45 or the Runge-Kutta-Fehlberg method. The Dormand-Prince method is another example of a higher-order method, which additionally uses adaptive stepsize control. For example, the 8-5-3 method combines 3rd- and 5th-order schemes to produce an 8th-order method. An implementation of this method is available in SciPy, which we will see in the next section.

An alternative method is to use more than one previous value of y_k to compute . Such methods are known as multistep methods, and can in general be written on the form

This formula means that to compute , the previous s values of y_k and f(x_k, y_k) are used (known as an s-step method). The choices of the coefficients a_n and b_n give rise to different multistep methods. Note that if , then the method is explicit, and if it is implicit.

For example, gives the general formula for an s-step BDF formula. where a_n and b_n are chosen to maximize the order of the accuracy the method by requiring that the method is exact for polynomials up to as high order as possible. This gives an equation system that can be solved for the unknown coefficients a_n and b_n. For example, the one-step BDF method with reduces to the backward Euler method, , and the two-step BDF method, , when solved for the coefficients (a₀, a₁, and b₂) becomes: . Higher-order BDF methods can also be constructed. SciPy provides a BDF solver that is recommended for stiff problems, because of its good stability properties.

Another family of multistep methods are the Adams methods, which result from the choice and , where again the remaining unknown coefficients are chosen to maximize the order of the method. Specifically, the explicit method with are known as Adams-Bashforth methods, and the implicit methods with are known as Adams-Moulton methods. For example, the one-step Adams-Bashforth and Adams-Moulton methods reduce to the forward and backward Euler methods, respectively, and the two-step methods are , and , respectively. Higher-order explicit and implicit methods can also be constructed in this way. Solvers using these Adams methods are also available in SciPy.

In general explicit methods are more convenient to implement and less computationally demanding to iterate than implicit methods, which in principle requires solving (a potentially nonlinear) equation in each iteration with an initial guess for the unknown . However, as mentioned earlier, implicit methods often are more accurate and have superior stability properties. A compromise that retain some of the advantages of both methods is to combine explicit and implicit methods in the following way: First compute using an explicit method, then use this as an initial guess for solving the equation for given by an implicit method. This equation does not need to be solved exactly, and since the initial guess from the explicit method should be quite good, a fixed number of iterations, using for example Newton’s method, could be sufficient. Methods like these, where the result form an explicit method is used to predict and an implicit method is used to correct the prediction, are called predictor-corrector methods.

Finally, an important technique that is employed by many advanced ODE solvers is adaptive stepsize, or stepsize control: The accuracy and stability of an ODE is strongly related to the stepsize h_k used in the iteration formula for an ODE method, and so is the computational cost of the solution. If the error in can be estimated together with the computation of itself, then it possible to automatically adjust the stepsize h_k so that the solver uses large economical stepsizes when possible, and smaller stepsizes when required. A related technique, which is possible with some methods, is to automatically adjust the order of the method, so that a lower order method is when possible, and a higher-order method is used when necessary. The Adams methods are examples of methods where the order can be changed easily.

There exist a vast variety of high-quality implementations of ODE solvers, and rarely should it be necessary to reimplement any of the methods discuss here. In fact, doing so would probably be a mistake, unless it is for educational purposes, or if ones primary interest is research on methods for numerical ODE solving. For practical purposes, it is advisable to use one of the many highly tuned and thoroughly tested ODE suites that already exists, most of which are available for free and as open source, and packaged into libraries such as SciPy. However, there are a large number of solvers to choose between, and to be able to make an informed decision on which one to use for a particular problem, and to understand many of their options, it is important to be familiar with the basic ideas and methods, and the terminology that is used to discuss them.

Numerical Integration of ODEs using SciPy

After the review of numerical methods for solving ODEs given in the previous section, we are now ready to explore the ODE solvers that are available in SciPy, and how to use them. The integrate module of SciPy provides two ODE solver interfaces: integrate.odeint and integrate.ode. The odeint function is an interface to the LSODA solver from ODEPACK,⁴ which automatically switches between an Adams predictor-corrector method for non-stiff problems and a BDF method for stiff problems. In contrast, the integrate.ode class provides an object-oriented interface to number of different solvers: the VODE and ZVODE solvers⁵ (ZVODE is a variant of VODE for complex-valued functions), the LSODA solver, and dopri5 and dop853, which are fourth and eighth order Dormand-Prince methods (that is, types of Runge-Kutta methods) with adaptive stepsize. While the object-oriented interface provided by integrate.ode is more flexible, the odeint function is in many cases simpler and more convenient to use. In the following we look at both these interfaces, starting with the odeint function.

The odeint function takes three mandatory arguments: a function for evaluating the right-hand side of the ODE on standard form, an array (or scalar) that specifies the initial condition for the unknown functions, and an array with values of independent variable where unknown function is to be computed. The function for the right-hand side of the ODE takes two mandatory arguments, and an arbitrary number of optional arguments. The required arguments are the array (or scalar) for the vector y(x) as first argument, and the value of x as second argument. For example, consider again the scalar ODE . To be able to plot the direction field for this ODE again, this time together with a specific solution obtained by numerical integration using odeint, we first define the SymPy symbols required to construct a symbolic expression for f (x, y(x)):

In [79]: x = sympy.symbols("x")
In [80]: y = sympy.Function("y")
In [81]: f = y(x)**2 + x

To be able to solve this ODE with SciPy’s odeint, we first and foremost need to define a Python function for f(x, y(x)) that takes Python scalars or NumPy arrays as input. From the SymPy expression f, we can generate such a function using sympy.lambdify with the 'numpy' argument⁶:

In [82]: f_np = sympy.lambdify((y(x), x), f)

Next we need to define the initial value y0, and a NumPy array with the values of discrete values of x for which to compute the function y(x). Here we the ODE starting at in both the positive and negative directions, using the NumPy arrays xp and xm, respectively. Note that to solve the ODE in the negative direction, we only need to create a NumPy array with negative increments. Now that we have set up the ODE function f_np, initial value y0, and array of x coordination, for example xp, we can integrate the ODE problem by calling integrate.odeint(f_np, y0, xp):

In [83]: y0 = 0
In [84]: xp = np.linspace(0, 1.9, 100)
In [85]: yp = integrate.odeint(f_np, y0, xp)
In [86]: xm = np.linspace(0, -5, 100)
In [87]: ym = integrate.odeint(f_np, y0, xm)

The results are two one-dimensional NumPy arrays ym and yp, of the same length as the corresponding coordinate arrays xm and xp (that is, 100), which contain the solution to the ODE problem at the specified points. To visualize the solution, we next plot the ym and yp arrays together with the direction field for the ODE. The result is shown in Figure 9-4, and it is apparent that the solution aligns (tangents) the lines in the direction field at every point in the graph, as expected.

In [88]: fig, ax = plt.subplots(1, 1, figsize=(4, 4))
    ...: plot_direction_field(x, y(x), f, ax=ax)
    ...: ax.plot(xm, ym, 'b', lw=2)
    ...: ax.plot(xp, yp, 'r', lw=2)

In the previous example we solved a scalar ODE problem. More often we are interested in vector-valued ODE problems (systems of ODEs). To see how we can solve that kind of problems using odeint, consider the Lokta-Volterra equations for the dynamics of a population of predator and prey animals (a classic example of coupled ODEs). The equations are and , where x(t) is the number of prey animals and y(t) is the number of predator animals, and the coefficients a, b, c, and d describe the rates of the processes in the model. For example, a is the rate at which prey animals are born, and d is the rate at which predators die. The b and c coefficients are the rates at which predators consume prey, and the rate at which the predator population grow at the expense of the prey population, respectively. Note that this is a nonlinear system of ODEs, because of the xy terms.

To solve this problem with odeint, we first need to write a function for the right-hand side of the ODE in vector form. For this case we have , which we can implement as a Python function in the following way:

In [89]: a, b, c, d = 0.4, 0.002, 0.001, 0.7
In [90]: def f(xy, t):
    ...:     x, y = xy
    ...:     return [a * x - b * x * y, c * x * y - d * y]

Here we have also defined variables and values for the coefficients a, b, c, and d. Note that here the first argument of the ODE function f is an array containing the current values of x(t) and y(t). For convenience, we first unpack these variables into separate variables x and y, which makes the rest of the function easier to read. The return value of the function should be an array, or list, that contains the values of the derivatives of x(t) and y(t). The function f must also take the argument t, with the current value of the independent coordinate. However, t is not used in this example. Once the f function is defined, we also need to define an array xy0 with the initial values x(0) and y(0), and an array t for the points at which we wish to compute the solution to the ODE. Here we use the initial conditions and , which corresponds to 600 prey animals and 400 predators at the beginning of the simulation.

In [91]: xy0 = [600, 400]
In [92]: t = np.linspace(0, 50, 250)
In [93]: xy_t = integrate.odeint(f, xy0, t)
In [94]: xy_t.shape
Out[94]: (250,2)

Calling integrate.odeint(f, xy0, t) integrates the ODE problem and returns an array or shape (250, 2), which contains ) and y(t) for each of the 250 values in t. The following code plots the solution as a function of time and in phase space. The result is shown in Figure 9-5.

In [95]: fig, axes = plt.subplots(1, 2, figsize=(8, 4))
    ...: axes[0].plot(t, xy_t[:,0], 'r', label="Prey")
    ...: axes[0].plot(t, xy_t[:,1], 'b', label="Predator")
    ...: axes[0].set_xlabel("Time")
    ...: axes[0].set_ylabel("Number of animals")
    ...: axes[0].legend()
    ...: axes[1].plot(xy_t[:,0], xy_t[:,1], 'k')
    ...: axes[1].set_xlabel("Number of prey")
    ...: axes[1].set_ylabel("Number of predators")

In the previous two examples, the function for the right-hand side of the ODE was implemented without additional arguments. In the example with the Lokta-Volterra equation, the function f used globally defined coefficient variables. Rather than using global variables, it is often convenient and elegant to implement the f function in such a way that it takes arguments for all its coefficient or parameters. To illustrate this point, let’s consider another famous ODE problem: the Lorenz equations, which is the following system of three coupled nonlinear ODEs, , and . These equations are known for their chaotic solutions, which sensitively depend on the values of the parameters σ, ρ, and β. If we wish to solve these equations for different values of these parameters, it is useful to write the ODE function so that it additionally takes the values of these variables as arguments. In the following implementation of f, the three arguments sigma, rho, and beta, for the correspondingly named parameters, have been added after the mandatory y(t) and t arguments:

In [96]: def f(xyz, t, sigma, rho, beta):
    ...:     x, y, z = xyz
    ...:     return [sigma * (y - x),
    ...:             x * (rho - z) - y,
    ...:             x * y - beta * z]

Next, we define variables with specific values of the parameters, the array with t values to compute the solution for, and the initial conditions for the functions x(t), y(t), and z(t).

In [97]: sigma, rho, beta = 8, 28, 8/3.0
In [98]: t = np.linspace(0, 25, 10000)
In [99]: xyz0 = [1.0, 1.0, 1.0]

This time when we call integrate.odeint, we need to also specify the args argument, which needs to be a list, tuple, or array with the same number of elements as the number of additional arguments in the f function we defined above. In this case there are three parameters, and we pass a tuple with the values of these parameters via the args argument when calling integrate.odeint. In the following we solve the ODE for three different set of parameters (but same initial conditions).

In [100]: xyz1 = integrate.odeint(f, xyz0, t, args=(sigma, rho, beta))
In [101]: xyz2 = integrate.odeint(f, xyz0, t, args=(sigma, rho, 0.6*beta))
In [102]: xyz3 = integrate.odeint(f, xyz0, t, args=(2*sigma, rho, 0.6*beta))

The solutions are stored in the NumPy arrays xyz1, xyz2, and xyz3. In this case these arrays have the shape (10000, 3), because the t array have 10000 elements and there are three unknown functions in the ODE problem. The three solutions are plotted in 3D graphs in the following code, and the result is shown in Figure 9-6. With small changes in the system parameters, the resulting solutions can vary greatly.

In [103]: from mpl_toolkits.mplot3d.axes3d import Axes3D
In [104]: fig, (ax1,ax2,ax3) = plt.subplots(1, 3, figsize=(12, 4),
     ...:                                   subplot_kw={'projection':'3d'})
     ...: for ax, xyz, c in [(ax1, xyz1, 'r'), (ax2, xyz2, 'b'), (ax3, xyz3, 'g')]:
     ...:     ax.plot(xyz[:,0], xyz[:,1], xyz[:,2], c, alpha=0.5)
     ...:     ax.set_xlabel('$x$', fontsize=16)
     ...:     ax.set_ylabel('$y$', fontsize=16)
     ...:     ax.set_zlabel('$z$', fontsize=16)
     ...:     ax.set_xticks([-15, 0, 15])
     ...:     ax.set_yticks([-20, 0, 20])
     ...:     ax.set_zticks([0, 20, 40])

The three examples we have looked at so far all use the odeint solver. This function takes a large number of optional arguments that can be used to fine tune the solver, including options for maximum number of allowed steps (hmax), the maximum order for the Adams (mxordn), and BDF (mxords) methods, just to mention a few. See the docstring for odeint for further information.

The alternative to odeint in SciPy is the object-oriented interface provided by the integrate.ode class. Like with the odeint function, to use the integrate.ode class we first need to define the right-hand side function for the ODE, define the initial state array and an array for the values of the independent variable at which we want to compute the solution. However, one small but important difference is that while the function for f(x, y(x)) to be used with odeint had to have the function signature f(y, x, ...), the corresponding function to be used with integrate.ode must have the function signature f(x, y, ...) (that is, the order of x and y is reversed).

The integrate.ode class can work with a collection of different solvers, and it has specific options for each solver. The docstring of integrate.ode describes the available solvers and their options. To illustrate how to use the integrate.ode interface, we first look at the following sets of coupled second-order ODEs:

These equations describe the dynamics of two coupled springs, where x₁(t) and x₂(t) are the displacement of two objects, with masses m₁ and m₂, from their equilibrium positions. The object at x₁ is connect to a fixed wall via a spring with spring constant k₁, and connected to the object at x₂ via a spring with spring constant k₂. Both objects are subject to damping forces characterized by γ₁ and γ₂, respectively. To solve this kind of problem with SciPy, we first have to write it in standard form, which we can do by introducing , , , and , which results in four coupled first-order equations:

The first task is to write a Python function that implements the function f(t, y(t)), which also takes the problem parameters as additional arguments. In the following implementation we bunch all the parameters into a tuple that is passed to the function as a single argument, and unpack it on the first line of the function body:

In [105]: def f(t, y, args):
     ...:     m1, k1, g1, m2, k2, g2 = args
     ...:     return [y[1], - k1/m1 * y[0] + k2/m1 * (y[2] - y[0]) - g1/m1 * y[1],
     ...:             y[3], - k2/m2 * (y[2] - y[0]) - g2/m2 * y[3]]

The return value of the function f is a list of length four, whose elements are the derivatives of the ODE functions y₀(t) to y₃(t). Next we create variables with specific values for the parameters, and pack them into a tuple args that can be passed to the function f. Like before, we also need to create arrays for the initial condition y0, and for the t values that we want to compute the solution to the ODE, t.

In [106]: m1, k1, g1 = 1.0, 10.0, 0.5
In [107]: m2, k2, g2 = 2.0, 40.0, 0.25
In [108]: args = (m1, k1, g1, m2, k2, g2)
In [109]: y0 = [1.0, 0, 0.5, 0]
In [110]: t = np.linspace(0, 20, 1000)

The main difference between using and integrate.odeint and integrate.ode start at this point. Instead of calling the odeint function, we now need to create an instance of the class integrate.ode, passing the ODE function f as an argument:

In [111]: r = integrate.ode(f)

Here we store the resulting solver instance in the variable r. Before we can start using it, we need to configure some of its properties. At a minimum, we need to set the initial state using the set_initial_value method, and if the function f takes additional arguments we need to configure those using the set_f_params method. We can also select solver using set_integrator method, which accept the following solver names as first argument: vode, zvode, lsoda, dopri5 and dop853. Each solver takes additional optional arguments. See the docstring for integrate.ode for details. Here we use the LSODA solver, and set the initial state and the parameters to the function f:

In [112]: r.set_integrator('lsoda');
In [113]: r.set_initial_value(y0, t[0]);
In [114]: r.set_f_params(args);

Once the solver is created and configured we can start solving the ODE step by step by calling r.integrate method, and the status of the integration can be queried using the method r.successful (which returns True as long as the integration is proceeding fine). We need to keep track of which point to integrate to, and we need to store results by ourselves:

In [115]: dt = t[1] - t[0]
     ...: y = np.zeros((len(t), len(y0)))
     ...: idx = 0
     ...: while r.successful() and r.t < t[-1]:
     ...:     y[idx, :] = r.y
     ...:     r.integrate(r.t + dt)
     ...:     idx += 1

This is arguably not as convenient as simply calling the odeint, but it offers extra flexibility that sometimes is exactly what is needed. In this example we stored the solution in the array y for each corresponding element in t, which is similar to what odeint would have returned. The following code plots the solution, and the result is shown in Figure 9-7.

In [116]: fig = plt.figure(figsize=(10, 4))
     ...: ax1 = plt.subplot2grid((2, 5), (0, 0), colspan=3)
     ...: ax2 = plt.subplot2grid((2, 5), (1, 0), colspan=3)
     ...: ax3 = plt.subplot2grid((2, 5), (0, 3), colspan=2, rowspan=2)
     ...: # x_1 vs time plot
     ...: ax1.plot(t, y[:, 0], 'r')
     ...: ax1.set_ylabel('$x_1$', fontsize=18)
     ...: ax1.set_yticks([-1, -.5, 0, .5, 1])
     ...: # x2 vs time plot
     ...: ax2.plot(t, y[:, 2], 'b')
     ...: ax2.set_xlabel('$t$', fontsize=18)
     ...: ax2.set_ylabel('$x_2$', fontsize=18)
     ...: ax2.set_yticks([-1, -.5, 0, .5, 1])
     ...: # x1 and x2 phase space plot
     ...: ax3.plot(y[:, 0], y[:, 2], 'k')
     ...: ax3.set_xlabel('$x_1$', fontsize=18)
     ...: ax3.set_ylabel('$x_2$', fontsize=18)
     ...: ax3.set_xticks([-1, -.5, 0, .5, 1])
     ...: ax3.set_yticks([-1, -.5, 0, .5, 1])

In addition to providing a Python function for the ODE function f(t, y(t)), we can also provide a Python function that computes the Jacobian matrix for a given t and y(t). The solver can, for example, use the Jacobian to solve more efficiently the system of equations that arise in implicit methods. To use a Jacobian function jac, like the one defined below for the current problem, we need to pass it to the integrate.ode class when it is created, together with the f function. If the Jacobian function jac takes additional arguments, those also have to be configured using the set_jac_params method in the resulting integrate.ode instance:

In [117]: def jac(t, y, args):
     ...:     m1, k1, g1, m2, k2, g2 = args
     ...:     return [[0, 1, 0, 0],
     ...:             [- k1/m2 - k2/m1, - g1/m1 * y[1], k2/m1, 0],
     ...:             [0, 0, 1, 0],
     ...:             [k2/m2, 0, - k2/m2, - g2/m2]]
In [118]: r = integrate.ode(f, jac)
In [119]: r.set_jac_params(args);

Python functions for both f(t, y(t)) and its Jacobian can conveniently be generated using SymPy’s lambdify, provided that the ODE problem first can be defined as a SymPy expression. This symbolic-numeric hybrid approach is a powerful method to solving ODE problems. To illustrate this approach, consider the rather complicated system of two coupled second-order and nonlinear ODEs for a double pendulum. The equations of motion for the angular deflection, θ₁(t) and θ₂(t), for the first and the second pendulum, respectively, are⁷:

The first pendulum is attached to a fixed support, and the second pendulum is attached the first pendulum. Here m₁ and m₂ are the masses, and l₁ and l₂ the lengths, of the first and second pendulum, respectively. We begin by defining SymPy symbols for the variables and the functions in the problem, and then construct the ode expressions:

In [120]: t, g, m1, l1, m2, l2 = sympy.symbols("t, g, m_1, l_1, m_2, l_2")
In [121]: theta1, theta2 = sympy.symbols("theta_1, theta_2", cls=sympy.Function)
In [122]: ode1 = sympy.Eq((m1+m2)*l1 * theta1(t).diff(t,t) +
     ...:                 m2*l2 * theta2(t).diff(t,t) +
     ...:                 m2*l2 * theta2(t).diff(t)**2 * sympy.sin(theta1(t)-theta2(t)) +
     ...:                 g*(m1+m2) * sympy.sin(theta1(t)))
     ...: ode1
Out[122]:  
In [123]: ode2 = sympy.Eq(m2*l2 * theta2(t).diff(t,t) +
     ...:                 m2*l1 * theta1(t).diff(t,t) * sympy.cos(theta1(t)-theta2(t)) -
     ...:                 m2*l1 * theta1(t).diff(t)**2 * sympy.sin(theta1(t) - theta2(t)) +
     ...:                 m2*g * sympy.sin(theta2(t)))
     ...: ode2
Out[123]:  

Now ode1 and ode2 are SymPy expressions for the two second-order ODE equations. Trying to solve these equations with sympy.dsolve is fruitless, and to proceed we need to use a numerical method. However, the equations as they stand here are not in a form that is suitable for numerical solution with the ODE solvers that are available in SciPy. We first have to write the system of two second-order ODEs as a system of four first-order ODEs on standard form. Rewriting the equations on standard form is not difficult, but can be tedious to do by hand. Fortunately we can leverage the symbolic capabilities of SymPy to automate this task. To this end we need to introduce new functions and , and and and rewrite the ODEs in terms of these functions. By creating a dictionary for the variable change, and use the SymPy function subs to perform the substitution using this dictionary, we can easily obtain the equations for y₂^'(t) and y₄^'(t):

In [124]: y1, y2, y3, y4 = sympy.symbols("y_1, y_2, y_3, y_4", cls=sympy.Function)
In [125]: varchange = {theta1(t).diff(t, t): y2(t).diff(t),
     ...:              theta1(t): y1(t),
     ...:              theta2(t).diff(t, t): y4(t).diff(t),
     ...:              theta2(t): y3(t)}
In [126]: ode1_vc = ode1.subs(varchange)
In [127]: ode2_vc = ode2.subs(varchange)

We also need to introduce two more ODEs for y₁^¢(t) and y₃^¢(t):

In [128]: ode3 = y1(t).diff(t) - y2(t)
In [129]: ode4 = y3(t).diff(t) - y4(t)

At this point we have four coupled first-order ODEs for the functions y₁ to y₄. It only remains to solve for the derivatives of these functions to obtain the ODEs in standard form. We can do this using sympy.solve:

In [130]: y = sympy.Matrix([y1(t), y2(t), y3(t), y4(t)])
In [131]: vcsol = sympy.solve((ode1_vc, ode2_vc, ode3, ode4), y.diff(t), dict=True)
In [132]: f = y.diff(t).subs(vcsol[0])

Now f is SymPy expression for the ODE function f (t, y(t)). We can display the ODEs using sympy.Eq(y.diff(t), f), but the result is rather lengthy and in the interest of space we do not show the output here. The main purpose of constructing f here is to convert it to a NumPy-aware function that can be used with integrate.odeint or integrate.ode. The ODEs are now on a form that we can create such a function using sympy.lambdify. Also, since we have an symbolic representation of the problem so far, it is easy to also compute the Jacobian and create a NumPy-aware function for it too. When using sympy.lambdify to create functions for odeint and ode, we have to be careful to put t and y in the correct order in the tuple that is passed to sympy.lambdify. Here we will use integrate.ode, so we need a function with the signature f(t, y, ...), and thus we pass the tuple (t, y) as first argument to sympy.lambdify.

In [133]: params = {m1: 5.0, l1: 2.0, m2: 1.0, l2: 1.0, g: 10.0}
In [134]: f_np = sympy.lambdify((t, y), f.subs(params), 'numpy')
In [135]: jac = sympy.Matrix([[fj.diff(yi) for yi in y] for fj in f])
In [136]: jac_np = sympy.lambdify((t, y), jac.subs(params), 'numpy')

Here we have also substituted specific values of the system parameters calling sympy.lambdify. The first pendulum is made twice as long and five times as heavy as the second pendulum. With the functions f_np and jac_np, we are now ready to solve the ODE using integrate.ode in the same manner as in the previous examples. Here we take the initial state to be and , and with the derivatives zero to zero, and we solve for the time interval [0, 20] with 1000 steps:

In [137]: y0 = [2.0, 0, 0, 0]
In [138]: t = np.linspace(0, 20, 1000)
In [139]: r = integrate.ode(f_np, jac_np).set_initial_value(y0, t[0])
In [140]: dt = t[1] - t[0]
     ...: y = np.zeros((len(t), len(y0)))
     ...: idx = 0
     ...: while r.successful() and r.t < t[-1]:
     ...:     y[idx, :] = r.y
     ...:     r.integrate(r.t + dt)
     ...:     idx += 1

The solution to the ODEs is now stored in the array y, which have the shape (1000, 4). When visualizing this solution, it is more intuitive to plot the positions of the pendulums in the x–y plane rather than their angular deflections. The transformation between the angular variables θ₁and θ₂ and x and y coordinates are: , ,, and :

In [141]: theta1_np, theta2_np = y[:, 0], y[:, 2]
In [142]: x1 = params[l1] * np.sin(theta1_np)
     ...: y1 = -params[l1] * np.cos(theta1_np)
     ...: x2 = x1 + params[l2] * np.sin(theta2_np)
     ...: y2 = y1 - params[l2] * np.cos(theta2_np)

Finally we plot the dynamics of the double pendulum as a function of time and in the plane. The result is shown in Figure 9-8. As expected, pendulum 1 is confined to move in on a circle (because of its fixed anchor point), while pendulum 2 has a much more complicated trajectory.

In [143]: fig = plt.figure(figsize=(10, 4))
     ...: ax1 = plt.subplot2grid((2, 5), (0, 0), colspan=3)
     ...: ax2 = plt.subplot2grid((2, 5), (1, 0), colspan=3)
     ...: ax3 = plt.subplot2grid((2, 5), (0, 3), colspan=2, rowspan=2)
     ...:
     ...: ax1.plot(t, x1, 'r')
     ...: ax1.plot(t, y1, 'b')
     ...: ax1.set_ylabel('$x_1, y_1$', fontsize=18)
     ...: ax1.set_yticks([-3, 0, 3])
     ...:
     ...: ax2.plot(t, x2, 'r')
     ...: ax2.plot(t, y2, 'b')
     ...: ax2.set_xlabel('$t$', fontsize=18)
     ...: ax2.set_ylabel('$x_2, y_2$', fontsize=18)
     ...: ax2.set_yticks([-3, 0, 3])
     ...:
     ...: ax3.plot(x1, y1, 'r')
     ...: ax3.plot(x2, y2, 'b', lw=0.5)
     ...: ax3.set_xlabel('$x$', fontsize=18)
     ...: ax3.set_ylabel('$y$', fontsize=18)
     ...: ax3.set_xticks([-3, 0, 3])
     ...: ax3.set_yticks([-3, 0, 3])

Summary

In this chapter we have explored various methods and tools for solving ordinary differential equations (ODEs) using the scientific computing packages for Python. ODEs show up in many areas of science and engineering – in particular in modeling and the description of dynamical systems – and mastering the techniques to solve ODE problems is therefore crucial part of the skillset of a computational scientist. In this chapter, we first looked at solving ODEs symbolically using SymPy, either with the sympy.dsolve function or using a Laplace transformation method. The symbolic approach is often a good starting point, and with the symbolic capabilities of SymPy many fundamental ODE problems can be solved analytically. However, for most practical problems there is no analytic solution, and the symbolic methods are then doomed to fail. Our remaining option is then to fall back on numerical techniques. Numerical integration of ODEs is a vast field in mathematics, and there exists numerous reputable methods for solving ODE problems. In this chapter we briefly reviewed methods for integrating ODEs, with the intent to introduce the concepts and ideas behind the Adams and BDF multistep methods that are used in the solvers provided by SciPy. Finally, we looked at how the odeint and ode solvers, available through the SciPy integrate module, can be used by solving a few example problems. Although most ODE problems eventually require numerical integration, there can be great advantages in using a hybrid symbolic-numerical approach, which use features from both SymPy and SciPy. The last example of this chapter is devoted to demonstrating this approach.

Further Reading

An accessible introduction to many methods for numerically solving ODE problems is given in a book by Heath. For a review of ordinary differential equations with code examples, see Chapter 11 in Numerical Recipes (see below). For a more detailed survey of numerical methods for ODEs, see, for example, the Atkinson book. The main implementations of ODE solvers that are used in SciPy are the VODE and LSODA solvers. The original source code for these methods is available from netlib at http://www.netlib.org/ode/vode.f and http://www.netlib.org/odepack, respectively. In addition to these solvers, there is also a well-known suite of solvers called sundials, which is provided by the Lawrence Livermore National Laboratory and available at http://computation.llnl.gov/casc/sundials/main.html. This suite also includes solvers of differential-algebraic equations (DAE). A Python interface for the sundials solvers is provided by the sckit.odes library, which can be obtained from http://github.com/bmcage/odes. The odespy library also provides a unified interface to many different ODE solvers. For more information about odespy, see the projects web site at http://hplgit.github.io/odespy/doc/web/index.html.

References

Atkinson, Kendall, Han, Weiman, & Stewart, David. (2009). Numerical Solution of Ordinary Differential Equations. New Jersey: Wiley.

Heath, M. T. Scientific Computing. (2002). 2nd ed. New York: McGraw-Hill.

Press, W. H., Teukolosky, S. A., Vetterling, W. T., & Flannery, B. P. (2007). Numerical Recipies. 3rd ed. New York: Cambridge University Press.

__________________

¹In the current version of SymPy, the ics keyword argument is only recognized by the power-series solver in dsolve. Solvers for other types of ODEs ignore the ics argument, and hence the need for the apply_ics function we defined and used earlier in this chapter.

²Or “white-box” solver, since SymPy is open source and the inner workings of dsolve is readily available for inspection.

³Recall that any ODE problem can be written as a system of first-order ODEs on this standard form.

⁴More information about ODEPACK is available at http://computation.llnl.gov/casc/odepack.

⁵The VODE and ZVODE solvers are available at netlib: http://www.netlib.org/ode.

⁶In this particular case, with a scalar ODE, we could also use the 'math' argument, which produces a scalar function using functions from the standard math library, but more frequently we will need array-aware functions, which we obtain by using the 'numpy' argument to sympy.lambdify.

⁷See http://scienceworld.wolfram.com/physics/DoublePendulum.html for details.