Chapter 7
Development of the Nonideal Op Amp Equations
Abstract
Applying feedback theory and Bode analysis to real-world op amp circuits reveals that real-world gain circuits behave differently than circuits constructed with ideal op amp models. In particular, the limitation on open-loop gain affects and reduces the gain of common op amp circuits. The open-loop response of an op amp forms an unbreachable limit to where an op amp can operate.
Keywords
Closed-loop gain; Closed-loop response; Open-loop gain; Open-loop response
7.1. Introduction
There are two types of error sources in op amps, and they fall under the general classification of DC and AC errors. Examples of DC errors are input offset voltage and input bias current. The DC errors stay constant over the usable op amp frequency range; therefore, the input bias current is 10 pA at 1 kHz and it is 10 pA at 10 kHz. Because of their constant and controlled behavior, DC errors are not considered until later chapters.
AC errors are flighty, so we address them here by developing a set of nonideal equations that account for AC errors. The AC errors may show up under DC conditions, but they get worse as the operating frequency increases. A good example of an AC error is common-mode rejection ratio (CMRR). Most op amps have a guaranteed CMRR specification, but this specification is only valid at DC or very low frequencies. Further inspection of the data sheet reveals that CMRR decreases as operating frequency increases. Several other specifications that fall into the category of AC specifications are output impedance, power supply rejection ratio, peak-to-peak output voltage, differential gain, differential phase, and phase margin.
Differential gain is the most important AC specification because the other AC specifications are derived from the differential gain. Until now, differential gain has been called op amp gain or op amp open-loop gain, and we shall continue with that terminology. Let the data sheet call it differential gain.
As shown in prior chapters, when frequency increases, the op amp gain decreases and errors increase. This chapter develops the equations that illustrate the effects of the gain changes. We start with a review of the basic canonical feedback system stability because the op amp equations are developed using the same techniques.
Amplifiers are built with active components such as transistors. Pertinent transistor parameters such as transistor gain are subject to drift and initial inaccuracies from many sources, so amplifiers being built from these components are subject to drift and inaccuracies. The drift and inaccuracy is minimized or eliminated by using negative feedback. The op amp circuit configuration employs feedback to make the transfer equation of the circuit independent of the amplifier parameters (well almost), and while doing this, the circuit transfer function is made dependent on external passive components. The external passive components can be purchased to meet almost any drift or accuracy specification; only the cost and size of the passive components limit their use.
Once feedback is applied to the op amp, it is possible for the op amp circuit to become unstable. Certain amplifiers belong to a family called internally compensated op amps; they contain internal capacitors that are sometimes advertised as precluding instabilities. Although internally compensated op amps should not oscillate when operated under specified conditions, many have relative stability problems that manifest themselves as poor phase response, ringing, and overshoot. The only absolutely stable internally compensated op amp is the one lying on the workbench without power applied! All other internally compensated op amps oscillate under some external circuit conditions.
Noninternally compensated or externally compensated op amps are unstable without the addition of external stabilizing components. This situation is a disadvantage in many cases because they require additional components, but the lack of internal compensation enables the top-drawer circuit designer to squeeze the last drop of performance from the op amp. You have two options: op amps internally compensated by the IC manufacturer or op amps externally compensated by you. Compensation, except that done by the op amp manufacturer, must be done external to the IC. Surprisingly enough, internally compensated op amps require external compensation for demanding applications.
Compensation is achieved by adding external components that modify the circuit transfer function so that it becomes unconditionally stable. There are several different methods of compensating an op amp, and as you might suspect, there are pros and cons associated with each method of compensation. After the op amp circuit is compensated, it must be analyzed to determine the effects of compensation. The modifications that compensation have on the closed-loop transfer function often determine which compensation scheme is most profitably employed.
7.2. Review of the Canonical Equations
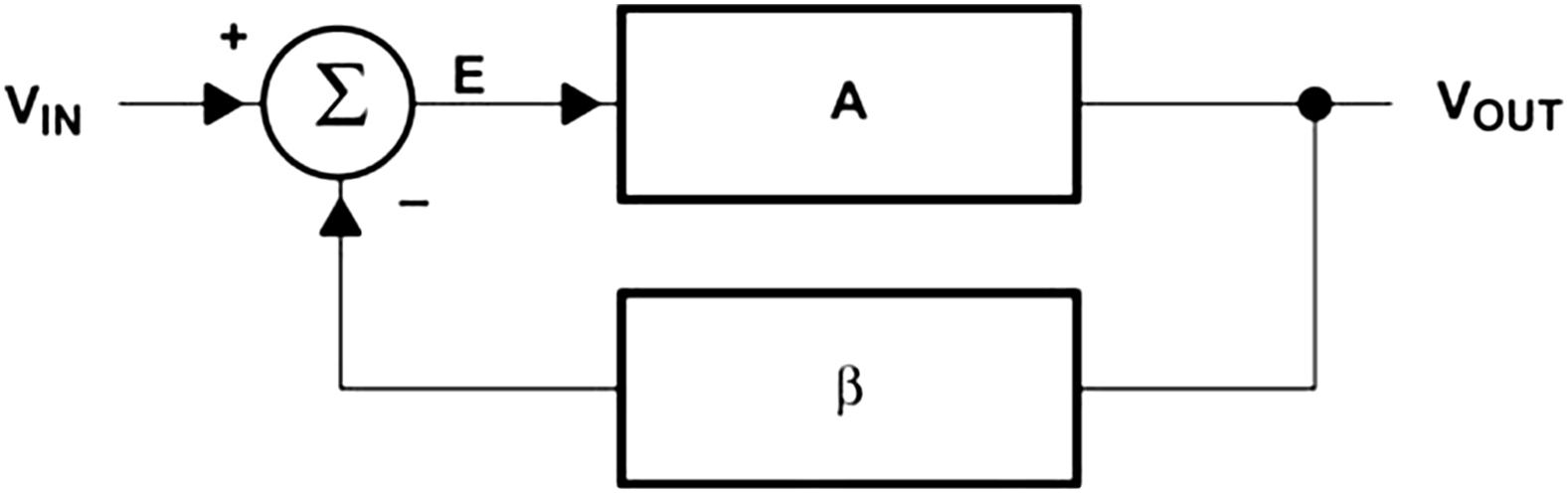
A block diagram for a generalized feedback system is repeated in Fig. 7.1. This simple block diagram is sufficient to determine the stability of any system.
The output and error equation development is repeated below:
Collecting terms yields Eq. (7.4):
Rearranging terms yields the classic form of the feedback equation.
Notice that Eq. (7.5) reduces to Eq. (7.6) when the quantity Aβ in Eq. (7.5) becomes very large with respect to one. Eq. (7.6) is called the ideal feedback equation because it depends on the assumption that Aβ ≫ 1, and it finds extensive use when amplifiers are assumed to have ideal qualities. Under the conditions that Aβ ≫ 1, the system gain is determined by the feedback factor β. Stable passive circuit components are used to implement the feedback factor, thus the ideal closed-loop gain is predictable and stable because β is predictable and stable.
The quantity Aβ is so important that it has been given a special name, loop gain. Consider Fig. 7.2; when the voltage inputs are grounded (current inputs are opened) and the loop is broken, the calculated gain is the loop gain, Aβ. Now, keep in mind that this is a mathematics of complex numbers, which have magnitude and direction. When the loop gain approaches −1, or to express it mathematically 1 ∠–180 degrees, Eq. (7.5) approaches infinity because 1/0 ⇒ ∞. The circuit output heads for infinity as fast as it can use the equation of a straight line. If the output were not energy limited the circuit would explode the world, but it is energy limited by the power supplies so the world stays intact.
Active devices in electronic circuits exhibit nonlinear behavior when their output approaches a power supply rail, and the nonlinearity reduces the amplifier gain until the loop gain no longer equals 1 ∠–180 degrees. Now the circuit can do two things: first, it could become stable at the power supply limit or second, it can reverse direction (because stored charge keeps the output voltage changing) and head for the negative power supply rail.
The first state where the circuit becomes stable at a power supply limit is named lockup; the circuit will remain in the locked up state until power is removed. The second state where the circuit bounces between power supply limits is named oscillatory. Remember, the loop gain, Aβ, is the sole factor that determines stability for a circuit or system. Inputs are grounded or disconnected when the loop gain is calculated, so they have no effect on stability. The loop gain criteria are analyzed in depth later.
Eqs. (7.1) and (7.2) are combined and rearranged to yield Eq. (7.7), which gives an indication of system or circuit error.
First, notice that the error is proportional to the input signal. This is the expected result because a bigger input signal results in a bigger output signal, and bigger output signals require more drive voltage. Second, the loop gain is inversely proportional to the error. As the loop gain increases the error decreases, thus large loop gains are attractive for minimizing errors. Large loop gains also decrease stability, thus there is always a trade-off between error and stability.
7.3. Noninverting Op Amps
A noninverting op amp is shown in Fig. 7.3. The dummy variable, VB, is inserted to make the calculations easier, and a is the op amp gain.
Eq. (7.8) is the amplifier transfer equation.
The output equation is developed with the aid of the voltage divider rule. Using the voltage divider rule assumes that the op amp impedance is low.
Rearranging terms in Eq. (7.10) yields Eq. (7.11), which describes the transfer function of the circuit.
 (7.11)
(7.11)Eq. (7.5) is repeated as Eq. (7.12) to make a term by term comparison of the equations easy.
By virtue of the comparison we get Eq. (7.13), which is the loop gain equation for the noninverting op amp. The loop gain equation determines the stability of the circuit. The comparison also shows that the open-loop gain, A, is equal to the op amp open-loop gain, a, for the noninverting circuit.
Eq. (7.13) is also derived with the aid of Fig. 7.4, which shows the open-loop noninverting op amp.
The test voltage, VTEST, is multiplied by the op amp open-loop gain to obtain the op amp output voltage, aVTEST. The voltage divider rule is used to calculate Eq. (7.15), which is identical to Eq. (7.14) after some algebraic manipulation.
7.4. Inverting Op Amps
The inverting op amp circuit is shown in Fig. 7.5. The dummy variable (VA) is inserted to make the calculations easier, and a is the op amp open-loop gain.
The transfer equation is given in Eq. (7.16):
The node voltage (Eq. 7.17) is obtained with the aid of superposition and the voltage divider rule. Eq. (7.18) is obtained by combining Eqs. (7.16) and (7.17).
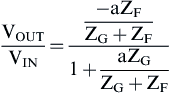 (7.18)
(7.18)Eq. (7.16) is the transfer function of the inverting op amp. By virtue of the comparison between Eqs. (7.18) and (7.14), we get Eq. (7.15) again, which is also the loop gain equation for the inverting op amp circuit. The comparison also shows that the open-loop gain (A) is different from the op amp open-loop gain (a) for the noninverting circuit.
The inverting op amp with the feedback loop broken is shown in Fig. 7.6, and this circuit is used to calculate the loop gain given in Eq. (7.19).
Several things must be mentioned at this point in the analysis. First, the transfer functions for the noninverting and inverting Eqs. (7.13) and (7.18), are different. For a common set of ZG and ZF values, the magnitude and polarity of the gains are different. Second, the loop gain of both circuits, as given by Eqs. (7.15) and (7.19), is identical. Thus, the stability performance of both circuits is identical although their transfer equations are different. This makes the important point that stability is not dependent on the circuit inputs. Third, the A gain block shown in Fig. 7.1 is different for each op amp circuit. By comparison of Eqs. (7.5), (7.11), and (7.18), we see that ANON-INV = a and AINV = aZF ÷ (ZG + ZF).
7.5. Differential Op Amps
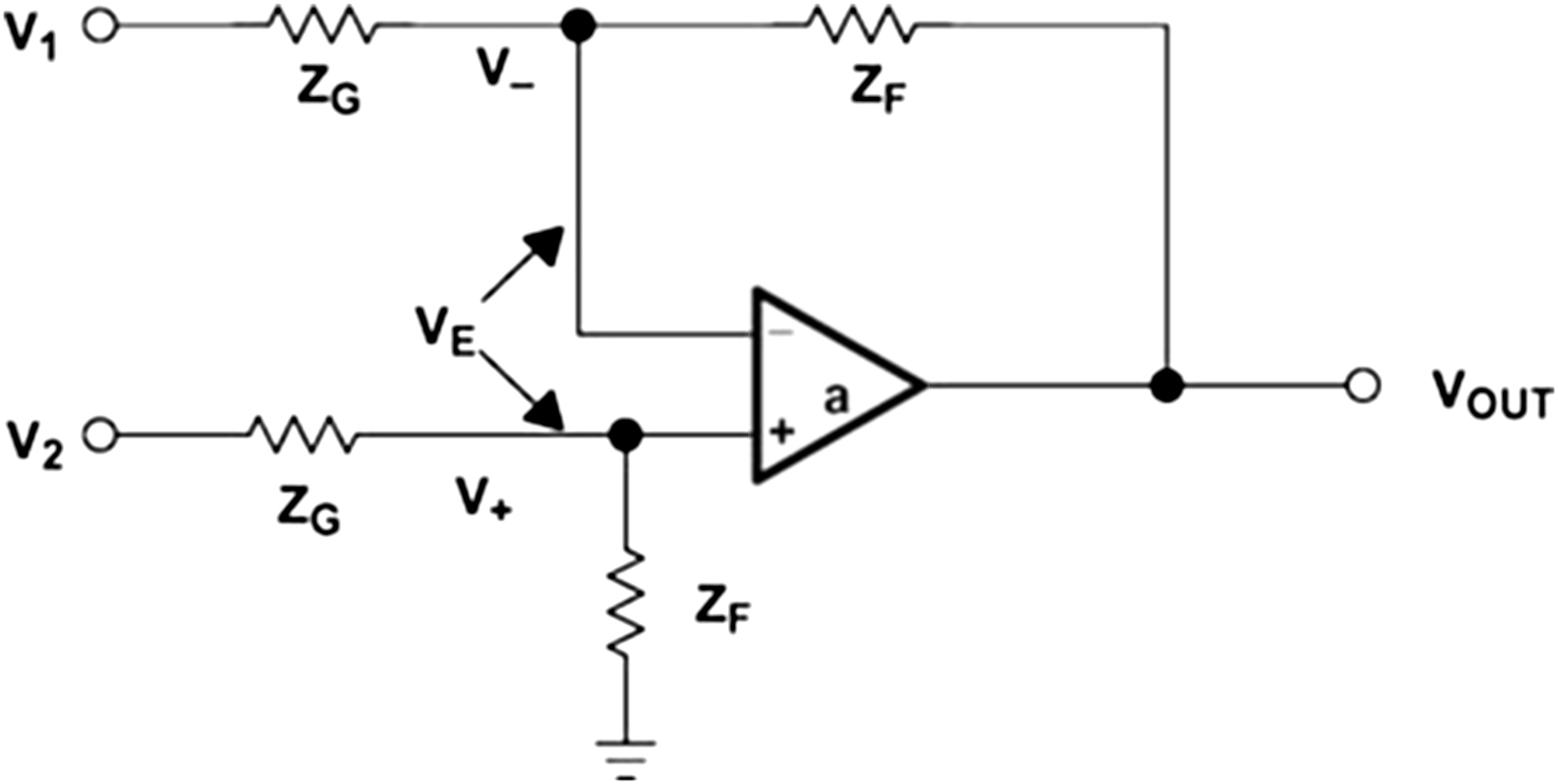
The differential amplifier circuit is shown in Fig. 7.7. The dummy variable, VE, is inserted to make the calculations easier, and a is the open-loop gain.
Eq. (7.20) is the circuit transfer equation.
The positive input voltage, V+, is written in Eq. (7.21) with the aid of superposition and the voltage divider rule.
The negative input voltage, V−, is written in Eq. (7.22) with the aid of superposition and the voltage divider rule.
After algebraic manipulation, Eq. (7.23) reduces to Eq. (7.24).
 (7.24)
(7.24)The comparison method reveals that the loop gain as shown in Eq. (7.25) is identical to that shown in Eqs. (7.13) and (7.19).
Again, the loop gain, which determines stability, is only a function of the closed loop and independent of the inputs.
7.6. Are You Smarter Than an Op Amp?
The discussion above is important enough that I need to bring a point to your attention again before we leave this chapter. The real-world equations for the noninverting and inverting gain stages (and the differential as well) impose some limitations on how you apply op amps. You must be aware of these limitations or you will not get the gain you are expecting!
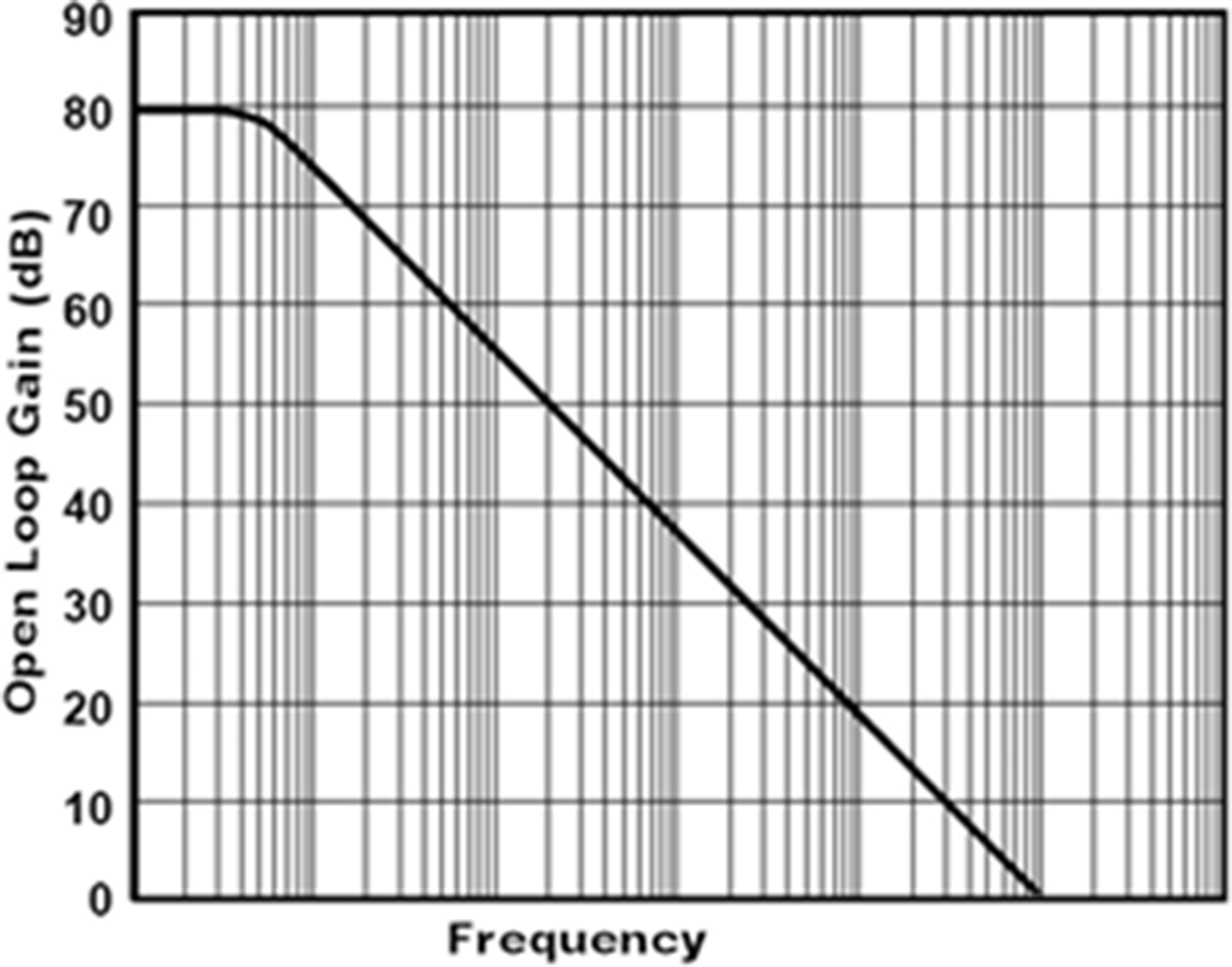
Let me reintroduce you to the open-loop Bode response of a typical voltage-feedback op amp (Fig. 7.8).
Notice that there is no frequency specified on the horizontal axis—this discussion applies to low-speed as well as high-speed op amps. You should consider three elements of the Bode plot.
• There is the region below and to the left of the open-loop response. This is the operating region of the op amp.
• There is the region above and to the right of the open-loop response. This is a region where you cannot operate an op amp.
Let me anger some semiconductor manufacturers and data sheet authors. If an open-loop response plot is not included in a data sheet, there is something to hide, i.e., not much of an operating region!
Repeating Eq. (7.11) for a noninverting op amp:
 (7.11)
(7.11)And Eq. (7.18) for an inverting op amp stage:
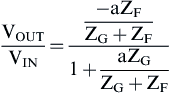 (7.18)
(7.18)Those equations are ugly! But when a ≫ the closed-loop gain at a given frequency, the approximations you are used to work well enough. In all practicality, you almost never have to worry about this limitation. But if you try to make a high-gain and/or a high-frequency amplifier stage, these equations explain why you will not get the gain you expected.
For the inverting case, with an open-loop gain of 80 dB (Table 7.1).
When you attempt a gain of −1 with RF = RG, the open-loop gain only contributes 0.02% error. If you are using 1% resistors, the error will never be noticed. Even at a gain of −10, the error is only 0.1%, still lost in the resistor tolerance. But at a gain of −100, fully 40 dB below the open-loop response, the error has become 1% and could be noticeable in precision applications. You can compensate by tweaking resistors a bit, but do not outsmart yourself! Any thermal drift at all will amplify the errors, which will be dominated by the lower value resistor RG. The op amp bandwidth also has some thermal drift, changing the gain. By the time you attempt a gain of 10,000, the error balloons to 50% and no reasonable amount of tweaking will help. If you do something ridiculous like using 1 Ω for RG and 1 TΩ for RF, the highest gain the stage will provide is still less than −10,000. Just like the speed of light, you can theoretically get as close as you want to the open-loop response plot, but you can never achieve it.
Table 7.1
Real Inverting Op Amp Stage Gains for a = 80 dB
| a | RG | RF | Attempted | Actual | Error (%) |
| 10,000 | 100,000 | 100,000 | −1 | −0.9998 | −0.0200 |
| 10,000 | 10,000 | 100,000 | −10 | −9.9890 | −0.1099 |
| 10,000 | 1000 | 100,000 | −100 | −99.0001 | −0.9999 |
| 10,000 | 100 | 100,000 | −1000 | −909.0083 | −9.0992 |
| 10,000 | 10 | 100,000 | −10,000 | −4999.7500 | −50.0025 |
| 10,000 | 1 | 100,000 | −100,000 | −9090.8264 | −90.9092 |
| 10,000 | 1 | 1.00E + 12 | −1E + 12 | −9999.9999 | −100 |

Table 7.2
Real Noninverting Op Amp Stage Gains for a = 80 dB
| a | RG | RF | Attempted | Actual | Error (%) |
| 10,000 | 100,000 | 100,000 | 2 | 1.9996 | −0.0200 |
| 10,000 | 10,000 | 100,000 | 11 | 10.9879 | −0.1099 |
| 10,000 | 1000 | 100,000 | 101 | 99.9901 | −0.9999 |
| 10,000 | 100 | 100,000 | 1001 | 909.9173 | −9.0992 |
| 10,000 | 10 | 100,000 | 10,001 | 5000.2500 | −50.0025 |
| 10,000 | 1 | 100,000 | 100,001 | 9090.9174 | −90.9092 |
| 10,000 | 1 | 1.00E + 12 | 1E + 12 | 9999.9999 | −100 |
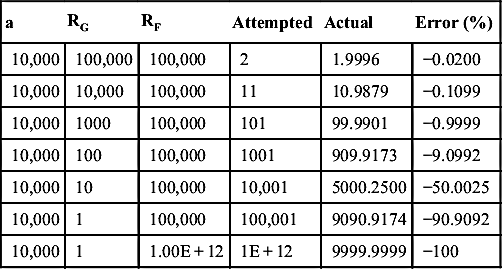
This is a similar table for the noninverting case (Table 7.2).
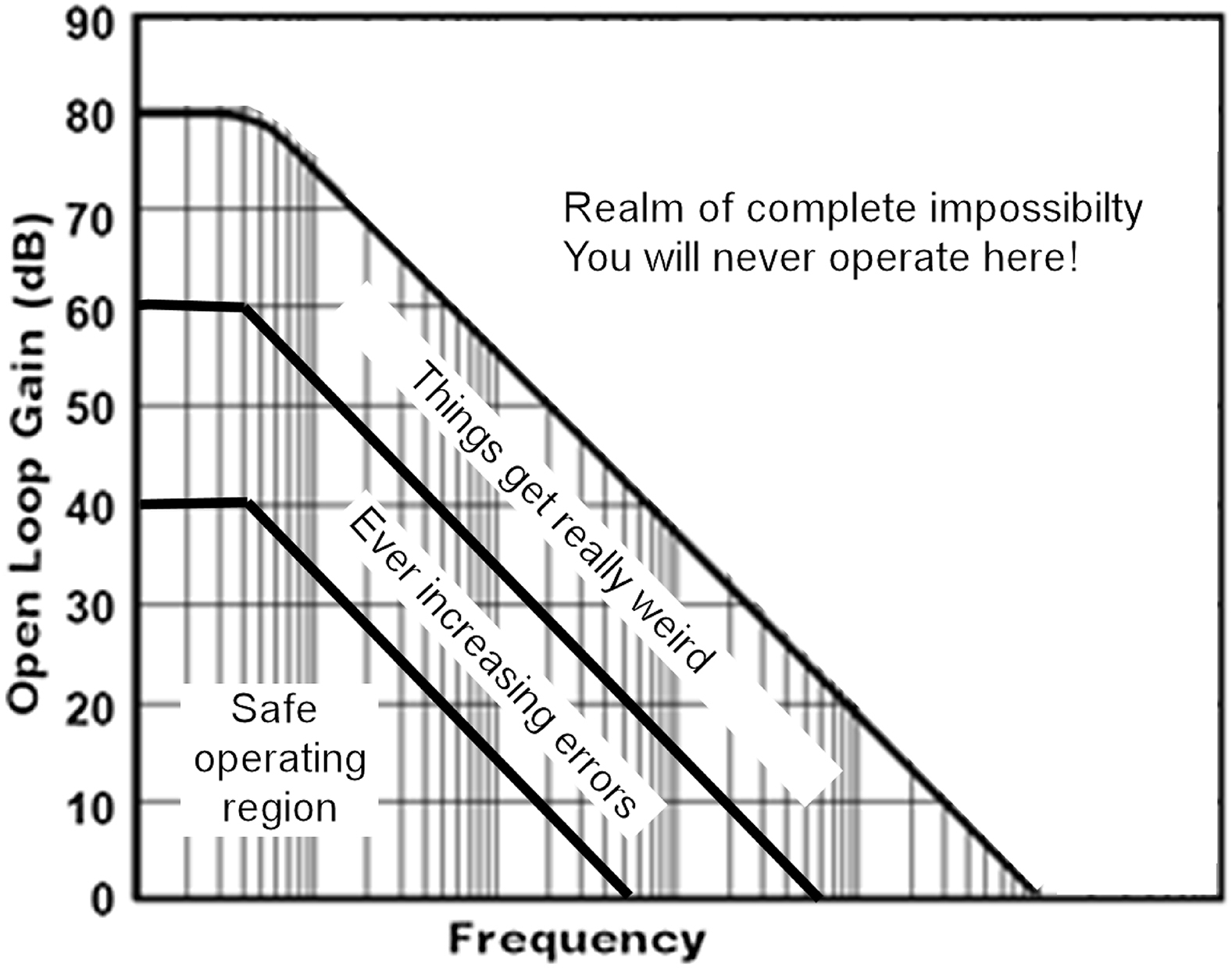
This may all sound esoteric and theoretical, far removed from your experience, but keep it in the back of your mind when you are designing gain stages. This is the way op amps really behave, and simple gain expressions you are used to are only approximations. They can mislead you. To give you a simple guide, think of open-loop Bode plots in the following way (Fig. 7.9).
Notice, there is not a lot of safe (errors ≤ 1%) operating region. All of the sudden, that high bandwidth amplifier does not have such a high bandwidth, does it? Just remember that log frequency plot above extends indefinitely in decades to the left, so you may just have to choose a higher bandwidth amplifier. Also, the starting open-loop gain on this op loop plot is 80 dB. You can find op amps with open-loop gains of 120 dB or more. Another thing to remember is the safe operating region is for gain stages only! Things get even stranger for filter circuits. The author recently discovered that a 1 GHz op amp was completely inadequate for a 1 MHz band-pass filter with a high Q! That is three decades—a factor of 1000—in frequency!
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.