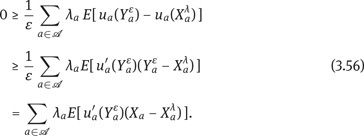3.6Microeconomic equilibrium

The aim of this section is to provide a brief introduction to the theory of market equilibrium. Prices of assets will no longer be given in advance. Instead, they will be derived from “first principles” in a microeconomic setting where different agents demand asset profiles in accordance with their preferences and with their budget constraints. These budget constraints are determined by a given price system. The role of equilibrium prices consists in adjusting the constraints in such a way that the resulting overall demand is matched by the overall supply of assets.

Consider a finite set A of economic agents and a convex set X ⊂ L0(Ω,F, P) of admissible claims. At time t = 0, each agent a ∈ A has an initial endowment whose discounted payoff at time t = 1 is described by an admissible claim

The aggregated claim

is also called the market portfolio. Agents may want to exchange their initial endowment Wa against some other admissible claim Xa ∈ X . This could lead to a new allocation (Xa)a∈A if the resulting total demand matches the overall supply:

Definition 3.58. A collection (Xa)a∈A ⊂ X is called a feasible allocation if it satisfies the market clearing condition

◊

The budget constraints will be determined by a linear pricing rule of the form

where φ is a price density, i.e., an integrable function on (Ω,F, P) such that φ > 0 P-a.s. and E[ |Wa| φ ] < ∞for all a ∈ A . To any such φ we can associate a normalized price measure Pφ ≈ P with density φE[ φ ]−1.

Remark 3.59. In the context of our one-period model of a financial market with d risky assets S1, . . . , Sd and a risk-free asset S0 ≡ 1 + r, Pφ is a risk-neutral measure if the pricing rule Φ is consistent with the given price vector = (π0, π), where π0 = 1. In this section, the pricing rule will be derived as an equilibrium price measure, given the agents’ preferences and endowments. In particular, this will amount to an endogenous derivation of the price vector π. In a situation where the structure of the equilibrium is already partially known in the sense that it is consistent with the given price vector π, the construction of a microeconomic equilibrium yields a specific choice of a martingale measure P∗, i.e., of a specific extension of π from the space V of attainable payoffs to a larger space of admissible claims.

◊

The preferences of agent a ∈ A are described by a utility function ua. Given the price density φ, an agent a ∈ A may want to exchange the endowment Wa for an admissible claim which maximizes the expected utility

over all X in the agent’s budget set

In this case, we will say that solves the utility maximization problem of agent a ∈ A with respect to the price density φ. The key problem is whether φ can be chosen in such a way that the requested profiles form a feasible allocation.

Definition 3.60. A price density φ∗ together with a feasible allocation is called an Arrow–Debreu equilibrium if each solves the utility maximization problem of agent a ∈ A with respect to φ∗.

◊

Thus, the price density φ∗ appearing in an Arrow–Debreu equilibrium decentralizes the crucial problem of implementing the global feasibility constraint (3.42). This is achieved by adjusting the budget sets in such away that the resulting demands respect the market clearing condition, even though the individual demand is determined without any regard to this global constraint.

Example 3.61. Assume that each agent a ∈ A has an exponential utility function with parameter αa > 0, and let us consider the unconstrained case

In this case, there is a unique equilibrium, and it is easy to describe it explicitly. For a given pricing measure P∗ ≈ P such that Wa ∈ L1(P∗) for all a ∈ A , the utility maximization problem for agent a ∈ A can be solved if and only if H (P∗|P) < ∞, and in this case the optimal demand is given by

where

see Example 3.35. The market clearing condition (3.42) takes the form

where α is defined via

Thus, a normalized equilibrium price density must have the form

and this shows uniqueness. As to existence, let us assume that

this condition is satisfied if, e.g., the random variables Wa are bounded from below. Define P∗ ≈ P via (3.44). Then

and the optimal profile for agent a ∈ A with respect to the pricing measure P∗ takes the form

Since

the allocation is feasible, and so we have constructed an Arrow–Debreu equilibrium. Thus, the agents share the market portfolio in a linear way, and in inverse proportion to their risk aversion.

Let us now return to our financial market model of Section 3.1. We assume that the initial endowment of agent a ∈ A is given by a portfolio ηa ∈ ℝd+1 so that the discounted payoff at time t = 1 is

In this case, the market portfolio is given bywith The optimal claim for agent a ∈ A in (3.45) takes the form

where = (1, π) and

Thus, we could have formulated the equilibrium problem within the smaller space X = V of attainable payoffs, and the resulting equilibrium allocation would have been the same. In particular, the extension of X from V to the general space L0(Ω,F, P) of admissible claims does not create a demand for derivatives in our present example.

◊

From now on we assume that the set of admissible claims is given by

and that the preferences of agent a ∈ A are described by a continuously differentiable utility function ua : (0,∞) → ℝ. We define

The initial endowments Wa are assumed to be nonnegative. Moreover, we assume

and

A function φ ∈ L1(Ω,F, P) such that φ > 0 P-a.s. is a price density if

note that this condition is satisfied as soon as φ is bounded, due to our assumption (3.46). Given a price density φ, each agent faces exactly the optimization problem discussed in Section 3.3 in terms of the price measure Pφ ≈ P. Thus, if is an equilibrium allocation with respect to the price density φ∗, feasibility implies 0 ≤ X∗a≤ W, and so it follows as in the proof of Corollary 3.42 that

with positive constants ca > 0. Note that the market clearing condition

will determine φ∗ as a decreasing function of W, and thus the optimal profiles will be increasing functions of W.

Before we discuss the existence of an Arrow–Debreu equilibrium, let us first illustrate the structure of such equilibria by the following simple examples. In particular, they show that an equilibrium allocation will typically involve nonlinear derivatives of the market portfolio W.

Example 3.62. Let us consider the constrained version of the preceding example where agents a ∈ A have exponential utility functions with parameters αa > 0. Define

and let P∗ be the measure defined via (3.44). For any agent a ∈ A such that

the unrestricted optimal profile

satisfies P-a.s. Thus, if all agents satisfy the requirement (3.48) then the unrestricted equilibrium computed in Example 3.61 is a forteriori an Arrow–Debreu equilibrium in our present context. In this case, there is no need for nonlinear derivatives of the market portfolio.

If some agents do not satisfy the requirement (3.48) then the situation becomes more involved, and the equilibrium allocation will need derivatives such as call options. Let us illustrate this effect in the simple setting where there are only two agents a ∈ A = {1, 2}. Suppose that agent 1 satisfies condition (3.48), while agent 2 does not. For c ≥ 0, we define the measure Pc ≈ P in terms of the density

where α is given by (3.43), and where the constants Z1 and Z2 are determined by the continuity condition

and by the normalization E[ φc ] = 1. Note that P0 = P∗ with P∗ as in (3.44). Consider the following equation for the parameter c,

where Both sides are continuous in c. As c increases from 0 to +∞, the left-hand side decreases from to 0, while goes from to E∞[W2 ] > 0. Thus, there exists a solution c of (3.49). Let us now check that

defines an equilibrium allocation with respect to the pricing measure Pc. Clearly, and are nonnegative and satisfy The budget condition for agent 2 is satisfied due to (3.49), and this implies the budget condition

for agent 1. Both are optimal since

with

Thus, agent 2 demands shares of a call option on the market portfolio W with strike c, agent 1 demands the remaining part of W, and so the market is cleared.

In the general case of a finite set A of agents, the equilibrium price measure has the following structure. There are levels 0=:c0 < ·· · < cN = ∞ with 1 ≤ N ≤ |A | such that the price density is given by

for i = 1, . . . , N, where

and where Ai (i = 1, . . . , N) are the increasing sets of agents which are active at the ith layer in the sense that Xa > 0on W ∈ (ci−1, ci]. At each layer (ci−1, ci], the active agents are sharing the market portfolio in inverse proportions to their risk aversion. Thus, the optimal profile a of any agent a ∈ A is given by an increasing piecewise linear function in W, and thus it can be implemented by a linear combination of call options with strikes ci.More precisely, an agent a ∈ Ai takes βi/αa shares of the spread

i.e., the agent goes long on a call option with strike ci−1 and short on a call option with strike ci.

◊

Example 3.63. Assume that all agents a ∈ A have preferences described by HARA utility functions so that

with 0 ≤ γa < 1. For a given price density φ, the optimal claims take the form

with constants ba > 0. If γa = γ for all a ∈ A , then the market clearing condition (3.42) implies

i.e., the equilibrium price density φ∗ takes the form

where Z is the normalizing constant, and so the agents demand linear shares of the market portfolio W. If risk aversion varies among the agents then the structure of the equilibrium becomes more complex, and it will involve nonlinear derivatives of the market portfolio. Let us number the agents so that A = {1, . . . , n} and γ1 ≥· ··≥ γn. Condition (3.50) implies

with some constants di, and where

satisfies β1 ≥· ··≥ βn = 1 with at least one strict inequality. Thus, each Xi is a convex increasing function of X n. In equilibrium, X n is a concave function of W determined by the condition

and the price density φ∗ takes the form

As an illustration, √we consider the special case “Bernoulli vs. Cramer”, where A = {1, 2} with u1(x) = x and u2(x) = log x, i.e., γ1 = and γ2 = 0; see Example 2.38. The solutions of (3.51) can be parameterized with c ≥ 0 such that

and

The corresponding price density takes the form

where Z(c) is the normalizing constant. Now assume that W −1 ∈ L 1(P), and let P∞denote the measure with density W−1E[W−1 ]−1. As 2cc increases from 0 to∞, increases continuously from 0 to E∞[W ], while Ec[W2 ] goes continuously from E0[W2 ] > 0 to E∞[W2 ] < E∞[W ]; here we use our assumption that P[Wa > 0] ≠ 0 for all a ∈ A . Thus, there is a c ∈ (0,∞) such that

and this implies that the budget constraint is satisfied for both agents. With this choice of the parameter c, is an equilibrium allocation with respect to the pricing measure Pc: Agent 2 demands the concave profile agent 1 demands the convex profile both in accordance with their budget constraints, and the market is cleared.

◊

Let us now return to our general setting, and let us prove the existence of an Arrow–Debreu equilibrium. Consider the following condition:

Remark 3.64. Condition (3.52) is clearly satisfied if

But it also includes HARA utility functions ua with parameter γa ∈ [0, 1) if we assume

in addition to our assumption (3.46).

◊

Theorem 3.65. Under assumptions (3.46) and (3.52), there exists an Arrow–Debreu equilibrium.

In a first step, we are going to show that an equilibrium allocation maximizes a suitable weighted average

of the individual utility functionals over all feasible allocations X = (Xa)a∈A . The weights λa are nonnegative, and without loss of generality we can assume that they are normalized so that the vector λ := (λa)a∈A belongs to the convex compact set

In a second step, we will use a fixed-point argument to obtain a weight vector and a corresponding price density such that the maximizing allocation satisfies the individual budget constraints.

Definition 3.66. A feasible allocation (Xa)a∈A is called λ-efficient for λ ∈ Λ if it maximizes Uλ over all feasible allocations.

◊

In view of (3.47), part (b) of the following lemma shows that the equilibrium allocation in an Arrow– Debreu equilibrium is λ-efficient for the vector where Thus, the existence proof for an Arrow–Debreu equilibrium is reduced to the construction of a suitable vector λ∗ ∈ Λ.

Lemma 3.67. (a) For any λ ∈ Λ there exists a unique λ-efficient allocation

(b) A feasible allocation (Xa)a∈A is λ-efficient if and only if it satisfies the first order conditions

with respect to some price density φ. In this case, (Xa)a∈A coincides with and the price density can be chosen as

(c) For each maximizes E[ ua(X) ] over all X ∈ X such that

Proof. (a): Existence and uniqueness follow from the general argument in Remark 3.37 applied to the set B of all feasible allocations and to the functional Uλ. Note that

for any feasible allocation, and that the right-hand side is finite due to our assumption (3.46). Moreover, by dominated convergence, Uλ is indeed continuous on B with respect to P-a.s. convergence.

(b): Let us first show sufficiency. If X = (Xa)a∈A is a feasible allocation satisfying the first order conditions, and Y = (Ya)a∈A is another feasible allocation then

using concavity of ua in the second step and the first order conditions in the third. This shows that X is λ-efficient.

Turning to necessity, consider the λ-efficient allocation for λ ∈ Λ and another feasible allocation For ε ∈ (0, 1], let Since is feasible, λ-efficiency of yields

Let us first assume (3.53); in part (d) of the proof we show how to modify the argument under the less restrictive condition (3.52). Using dominated convergence and (3.53), we may let ε ↓ 0 in the above inequality to conclude that for

we have

Note that φλ is a price density, since by (3.53)

Take a feasible allocation (Xa)a∈A such that

for example, we can enumerate A := {1, . . . , |A |} and take Xa := W{T=a} where

In view of (3.57), we see that

This implies on which is equivalent to the first order condition (3.54) with respect to φλ.

(c): In order to show optimality of we may assume without loss of generality that aand λhence λa > 0. Thus, the first order condition with respect to φλ takes the form

due to our convention (3.23) and the fact that which guarantees the validity of (3.60) also on By Corollary 3.42, solves the optimization problem for agent a ∈ A under the constraint

(d): If (3.53) is replaced by (3.52), then we first need an additional argument in order to pass from (3.56) to (3.57). Note first that by Fatou’s lemma,

On the other hand, since

by (3.52), we have for all x ≥ 0. This implies

and also

since Thus, dominated convergence aaλεimplies

and this concludes the proof of (3.57).

By (3.61), we have

Hence E[ φλ W ] < ∞ follows by taking in (3.57) a feasible allocation (Xa)a∈A which is as in (3.58). We furthermore get (3.59), which yields as in part (b) the first order conditions (3.54).

It remains to show that φλ is integrable in order to conclude that φλ is a price density. Our assumption (3.52) implies

and so it is enough to show that F ≥ φλ. Since feasibility and λa ≤ 1 imply

hence

After these preliminaries, we are now in a position to prove the existence of an Arrow– Debreu equilibrium. Note that for each λ ∈ Λ the λ-efficient allocation and the price density φλ would form an Arrow– Debreu equilibrium if

If this is not the case, then we can replace λ by the vector g(λ) = ga(λ)a∈A defined by

where V is given by (3.61). Note that g(λ) ∈ Λ: Since the first order conditions (3.54) together with (3.61) imply

we have ga(λ) ≥ 0, and follows by feasibility. Thus, we increase the weights of agents which were allocated less than they could afford. Clearly, any fixed point of the map g : Λ → Λ will satisfy condition (3.63) and thus yield an Arrow–Debreu equilibrium.

Proof of Theorem 3.65. (a): The set Λ is convex and compact. Thus, the existence of a fixed point of the map g : Λ → Λ follows from Brouwer’s fixed point theorem as soon as we can verify that g is continuous; see, for instance, Corollary 16.52 in [3] for a proof of Brouwer’s fixed point theorem. Suppose that the sequence (λn) ⊂ Λ converges to λ ∈ Λ. In part (c) we show that Xn := Xλn and φn := φλn converge P-a.s. to Xλ and φλ, respectively. We will show next that we may apply the dominated convergence theorem, so that

and

and this will prove the continuity of g. To verify the assumptions of the dominated convergence theorem, note that

where F is as in (3.62). Moreover,

Thus, φn Wa and φn Xn are bounded by WF ∈ L1(P).

(b): By our convention (3.23), the map f : Λ × [0,∞] → [0,∞] defined by

is continuous. If we fix λ ∈ Λ, then the function f (λ, ·) is continuous on [0,∞] and strictly decreasing on (a(λ), b(λ)) where

Moreover, f (λ, y) = ∞ for y ≤ a(λ) and f (λ, y) = 0 for y ≥ b(λ). Hence, for each w ∈ (0,∞) there exists exactly one solution yλ ∈ (a(λ), b(λ)) of the equation

Recall that [0,∞] can be regarded as a compact topological space. To see that yλ depends continuously on λ ∈ Λ, take a sequence λn → λ and a subsequence (λnk ) such that the solutions yk = yλnk of f (λnk , y) = w converge to some limit y∞ ∈ [a(λ), b(λ)]. By continuity of f ,

and so y∞ must coincide with yλ.

(c): Recall from (3.60) that

for any a ∈ A . By feasibility,

Thus, φλn converges P-a.s. to φλ as λn → λ due to part (b), and so Xλn converges P-a.s. to Xλ due to (3.64). This completes the proof in (a) that the map g is continuous.

Remark 3.68. In order to simplify the exposition, we have restricted the discussion of equilibrium prices to contingent claims with payoff at time t = 1. We have argued in terms of discounted payoffs, and so we have implicitly assumed that the interest rate r has already been fixed. From an economic point of view, also the interest rate should be determined by an equilibrium argument. This requires an intertemporal extension of our setting, which distinguishes between deterministic payoffs y at time t = 0 and nominal contingent payoffs Y at time t = 1. Thus, we replaceby the space

A pricing rule is given by a linear functional on Y of the form

where φ0 ∈ (0,∞) and φ is a price density as before. Any such price system specifies an interest rate for transferring income from time t = 0 to time t = 1. Indeed, comparing the forward price c · E[ φ ] for the fixed amount c to be delivered at time 1 with the spot price c · φ0 for the amount c made available at time 0, we see that the implicit interest rate is given by

If we describe the preferences of agent a ∈ A by a utility functional of the form

with smooth utility functions ua,0 and ua,1, then we can show along the lines of the preceding discussion that an Arrow–Debreu equilibrium exists in this extended setting. Thus, we obtain an equilibrium allocation and an equilibrium price system such that each maximizes the functional Ua in the agent’s budget set determined by an initial endowment in Y and by the pricing rule Φ∗. In particular, we have then specified an equilibrium interest rate r∗. Normalizing the price system to and defining P∗ as a probability measure with density φ∗/E[ φ∗ ],we see that the price at time t = 0 of a contingent claim with nominal payoff Y ≥ 0 at time t = 1 is given as the expectation

of the discounted claim with respect to the measure P∗.

◊

Let us now extend the discussion to situations where agents are heterogeneous not only in their utility functions but also in their expectations. Thus, we assume that the preferences of agent a ∈ A are described by a Savage functional of the form

where Qa is a probability measure on (Ω,F) which is equivalent to P. In addition to our assumption

we assume that

As before, a feasible allocation together with a price density φ∗ is called an Arrow–Debreu equilibrium if each maximizes the functional Ua on the budget set of agent a ∈ A , which is determined by φ∗.

Theorem 3.69. Under assumptions (3.46), (3.65), and (3.66), there exists an Arrow– Debreu equilibrium.

Proof. For any λ ∈ Λ, the general argument of Remark 3.37 yields the existence of a λ-efficient allocation i.e., of a feasible allocation which maximizes the functional

over all feasible allocations X = (Xa)a∈A . Since

can be viewed as a λ-efficient allocation in the model where agents have random utility functions of the form

while their expectations are homogeneous and given by P. In view of Corollary 3.43, it follows as before that Xλ satisfies the first order conditions

with

and that satisfies

for all Ya in the budget set of agent a ∈ A . The remaining arguments are essentially the same as in the proof of Theorem 3.65.