6American contingent claims
So far, we have studied European contingent claims whose payoff is due at a fixed maturity date. In the case of American options, the buyer can claim the payoff at any time up to the expiration of the contract.
First, we take the point of view of the seller, whose aim is to hedge against all possible claims of the buyer. In Section 6.1, this problem is solved under the assumption of market completeness, using the Snell envelope of the contingent claim. The buyer tries to choose the best date for exercising the claim, contingent on the information available up to that time. Since future prices are usually unknown, a formulation of this problem will typically involve subjective preferences. If preferences are expressed in terms of expected utility, the choice of the best exercise date amounts to solving an optimal stopping problem. In the special case of a complete market model, any exercise strategy which maximizes the expected payoff under the unique equivalent martingale measure turns out to be optimal even in an almost sure sense.
In Section 6.3, we characterize the set of all arbitrage-free prices of an American contingent claim in an incomplete market model. This involves a lower Snell envelope of the claim, which is analyzed in Section 6.5, using the fact that the class of equivalent martingale measures is stable under pasting. This notion of stability under pasting is discussed in Section 6.4 in a general context, and in Section 6.5 we point out its connection with the time-consistency of dynamic risk measures. This connection will be discussed systematically in Chapter 11. The results on lower Snell envelopes can also be regarded as a solution to the buyer’s optimal stopping problem in the case where preferences are described by robust Savage functionals. Moreover, these results will be used in the theory of superhedging of Chapter 7.
6.1Hedging strategies for the seller
Throughout this chapter we will continue to use the setting described in Section 5.1. We start by introducing the Doob decomposition of an adapted process and the notion of a supermartingale.
Proposition 6.1. Let Q be a probability measure on (Ω,FT), and suppose that Y is a stochastic process that is adapted to the filtration (Ft)t=0,...,T and satisfies Yt ∈ L1(Q) for all t. Then there exists a unique decomposition
where M is a Q-martingale and A is a process such that A0 = 0 and (At)t=1,...,T is predictable. The decomposition (6.1) is called the Doob decomposition of Y with respect to the probability measure Q.
Then A is predictable and M t := Yt + At is a Q-martingale. Clearly, any process A with the required properties must satisfy (6.2), so the uniqueness of the decomposition follows.
Definition 6.2. Let Q be a probability measure on (Ω,FT) and suppose that Y is an adapted process such that Yt ∈ L1(Q) for all t. Denote by Y = M − A the Doob decomposition of Y.
(a) Y is called a Q-supermartingale if A is increasing.
(b) Y is called a Q-submartingale if A is decreasing.
◊
Clearly, a process is a martingale if and only if it is both a supermartingale and a submartingale, i.e., if and only if A ≡ 0. The following exercise gives equivalent characterizations of the supermartingale property of a process Y.
Exercise 6.1.1. Let Y be an adapted process with Yt ∈ L1(Q) for all t. Show that the following conditions are equivalent:
(a) Y is a Q-supermartingale.
(b) Ys ≥ EQ[ Yt | Fs ] for 0 ≤ s ≤ t ≤ T.
(c) Yt−1 ≥ EQ[ Yt | Ft−1 ] for t = 1, . . . , T.
(d) −Y is a Q-submartingale.
◊
Exercise 6.1.2. Let Y be a nonnegative Q-supermartingale. Show that for 0 ≤ s ≤ T − t we have Yt+s = 0 Q-a.s. on {Yt = 0}.
◊
We now return to the market model introduced in Section 5.1. An American option, or American contingent claim, corresponds to a contract which is issued at time 0 and which obliges the seller to pay a certain amount Cτ ≥ 0 if the buyer decides at time τ to exercise the option. The choice of the exercise time τ is entirely up to the buyer, except that the claim is automatically exercised at the “expiration date” of the claim. The American contingent claim can be exercised only once: It becomes invalid as soon as the payoff has been claimed by the buyer. This concept is formalized as follows:
Definition 6.3. An American contingent claim is a nonnegative adapted process C = (Ct)t=0,...,T on the filtered space (Ω, (Ft)t=0,...,T).
◊
For each t, the random variable C t is interpreted as the payoff of the American contingent claim if the claim is exercised at time t. The time horizon T plays the role of the expiration date of the claim. The possible exercise times for C are not limited to fixed deterministic times t ∈ {0. . . . , T}; the buyer may exercise the claim in a way which depends on the scenario ω ∈ Ω of the market evolution.
Definition 6.4. An exercise strategy for an American contingent claim C is an FT-measurable random variable τ taking values in {0, . . . , T}. The payoff obtained by using τ is equal to
◊
Example 6.5. An American put option on the ith asset and with strike K > 0 pays the amount
if it is exercised at time t. The payoff at time t of the corresponding American call option is given by
Clearly, the American call option is “out of the money” (i.e., has zero payoff) if the corresponding American put is “in the money” (i.e., has nonzero payoff). It is therefore a priori clear that the respective owners of Cput and Ccall will usually exercise their claims at different times. In particular, there will be no put-call parity for American options.
◊
Similarly, one defines American versions of most options mentioned in the examples of Section 5.3. Clearly, the value of an American option is at least as high as the value of the corresponding European option with maturity T.
Remark 6.6. It should be emphasized that the concept of American contingent claims can be regarded as a generalization of European contingent claims: If CE is a European contingent claim, then we can define a corresponding American claim CA by
◊
Example 6.7. A Bermuda option can be exercised by its buyer at each time of a predetermined subset 
⊂ {0, . . . , T}. For instance, a Bermuda call option pays the amount 
if it is exercised at some time t ∈ . Thus, a Bermuda option is a financial instrument “between” an American option with = {0, . . . , T} and a European option with = {T}, just as Bermuda lies between America and Europe; hence the name “Bermuda option”. A Bermuda option can be regarded as a particular American option C that pays the amount Ct = 0 for t / ∈ .
◊
The process
of discounted payoffs of C will be called the discounted American claim associated with C. As far as the mathematical theory is concerned, the discounted American claim H will be the primary object. For certain examples it will be helpful to keep track of the numéraire and, thus, of the payoffs Ct prior to discounting.
In this section, we will analyze the theory of hedging American claims in a complete market model. That is, we assume that
Under this assumption, we will construct a suitable trading strategy that permits the seller of an American claim to hedge against the buyer’s discounted claim Hτ. Let us first try to characterize the minimal amount of capital Ut which will be needed at time t ∈ {0, . . . , T}. Since the choice of the exercise time τ is entirely up to the buyer, the seller must be prepared to pay at any time t the current payoff H t of the option. This amounts to the condition Ut ≥ H t. Moreover, the amount Ut must suffice to cover the purchase of the hedging portfolio for the possible payoffs H u for u > t. Since the latter condition is void at maturity, we require
At time T−1, our first requirement on UT−1 reads UT−1 ≥ H T−1. The second requirement states that the amount UT−1 must suffice for hedging the claim HT in case the option is not exercised before time T. Due to our assumption of market completeness, the latter amount equals
Thus,
is the minimal amount that fulfills both requirements. Iterating this argument leads to the following recursive scheme for Ut:
Definition 6.8. The process UP∗ := U defined by the recursion (6.5) is called the Snell envelope of the process H with respect to the measure P∗.
◊
Example 6.9. Let HE be a discounted European claim. Then the Snell envelope with respect to P∗ of the discounted American claim HA associated with HE via (6.3) satisfies
Thus, U is equal to the value process of a replicating strategy for HE.
◊
Clearly, a Snell envelope UQ can be defined for any probability measure Q on (Ω,FT) and for any adapted process H that satisfies the following integrability condition:
In our finite-time setting, this condition is equivalent to
If Q = P∗, then assumption (6.4) and Theorem 5.37 imply that the probability space (Ω,F, Q) has a finite structure so that the integrability condition (6.6) is satisfied automatically. For later applications, the following proposition is stated for a general measure Q, and we do not assume (6.4) here.
Proposition 6.10. Let H be an adapted process such that (6.6) holds. Then the Snell envelope UQ of H with respect to Q is the smallest Q-supermartingale dominating H: If is another Q-supermartingale such that 
t ≥ Ht Q-a.s. for all t, then
Q-a.s. for all t.
Proof. Since 
backward induction yields that 
L1(Q) for all t. Moreover, it follows from the definition of UQ that 
so that UQ is indeed a supermartingale. If is another supermartingale dominating H, then 
We now proceed by backward induction on t. If we already know that 
then
Adding our assumption t−1 ≥ H t−1 yields that
and the result follows.
Let us now return to the setting of a complete market model satisfying P = {P∗}. Proposition 6.10 illustrates how the seller can (super-) hedge a discounted American claim H by using the Doob decomposition
of the Snell envelope UP∗ with respect to P∗. Then M is a P∗-martingale, A is increasing, and (At)t=1,...,T is predictable. Since we assume the completeness of the market model, Theorem 5.38 yields the representation of the martingale Mas the discrete-time “stochastic integral” of a suitable d-dimensional predictable process ξ:
It follows that
By adding a numéraire component ξ0 such that 
= (ξ0, ξ) becomes a self-financing trading strategy with initial investment 
we obtain a (super-) hedge for H, namely a self-financing trading strategy whose value process V satisfies
Thus, 
may be viewed as the resulting capital at each time t if we use the self-financing strategy , combined with a refunding scheme where we withdraw successively the amounts defined by the increments of A. In fact, 
is the minimal investment at time t for which one can purchase a hedging strategy such that (6.8) holds. This follows from our next result.
Theorem 6.11. Let H be a discounted American claim with Snell envelope UP∗ . Then there exists a d-dimensional predictable process ξ such that
Moreover, any Ft-measurable random variable t which, for some predictable ξ, satisfies (6.9) in place of 
is such that
Thus, 
is the minimal amount of capital which is necessary to hedge H from time t up to maturity.
Proof. Due to the argument preceding the statement of this theorem, UP∗ satisfies (6.9) for ξ as in (6.7). Now suppose that t is Ft-measurable, that 
is predictable, and that
For t = 0, one can therefore use Doob’s systems theorem, Theorem 5.14, to conclude that V is a martingale dominating H. Proposition 6.10 thus yields 
for all u and, in particular, 
The following alternative argument works for all t ≥ 0. We proceed by backward induction on u. First, 
holds by assumption. Next, we assume that 
for some u ≥ t. Since our market model is complete, Theorem 5.37 implies that is bounded. Hence, we get
It follows that
6.2Stopping strategies for the buyer
In this section, we take the point of view of the buyer of an American contingent claim. Thus, our aim is to optimize the exercise strategy. It is natural to assume that the decision to exercise the claim at a particular time t depends only on the market information available at t. This constraint can be formulated as follows:
Definition 6.12. A function τ : Ω → {0, 1, . . . , T} ∪ {+∞} is called a stopping time if {τ = t} ∈ Ft for t = 0, . . . , T.
◊
In particular, the constant function τ ≡ t is a stopping time for fixed t ∈ {0, . . . , T}.
Exercise 6.2.1. Show that a function τ : Ω → {0, 1, . . . , T}∪{+∞} is a stopping time if and only if {τ ≤ t} ∈ Ft for each t. Show next that, if τ and σ are two stopping times, then the following functions are also stopping times:
Example 6.13. Atypical example of a nontrivial stopping time is the first time at which an adapted process Y exceeds a certain level c:
In fact,
for t = 0, . . . , T. This example also illustrates the role of the value +∞ in Definition 6.12: We have τ(ω) = +∞ if, for this particular ω, the criterion that triggers τ is not met for any t ∈ {0, . . . , T}.
◊
Definition 6.14. For any stochastic process Y and each stopping time τ we denote by Yτ the process stopped in τ:
◊
It follows from the definition of a stopping time that Yτ is an adapted process if Y is. Informally, the following basic theorem states that a martingale cannot be turned into a favorable game by using a clever stopping strategy. This result is often called Doob’s stopping theorem or the optional sampling theorem. Recall that we assume F0 = {∅, Ω}.
Theorem 6.15. Let M be an adapted process such that M t ∈ L1(Q) for each t. Then the following conditions are equivalent:
(a) M is a Q-martingale.
(b) For any stopping time τ the stopped process M τ is a Q-martingale.
(c) EQ[ Mτ∧T ] = M0 for any stopping time τ.
Proof. (a)⇒(b): Note that
We can thus use Doob’s systems theorem, Theorem 5.14, to conclude that M τ is a martingale. A direct argument goes as follows: Since {τ > t}∈ Ft, we obtain that
(b)⇒(c): This follows simply from the fact that the expectation of M τt is constant in t.
(c)⇒(a): We need to show that if t < T, then
for each A ∈ Ft, where we use again the notation EQ[Mt; A ] = EQ[Mt
A ]. Fix A ∈ Ft and define a stopping time τ as
We obtain that
Using the constant stopping time T instead of τ yields that
Subtracting the latter identity from the previous one yields (6.10).
Exercise 6.2.2. Let Y = M − A be the Doob decomposition with respect to Q of an adapted process Y with Yt ∈ L1(Q) (t = 0, . . . , T), and let τ be a stopping time. Show that Yτ = M τ − Aτ is the Doob decomposition of Yτ.
◊
Corollary 6.16. Let U be an adapted process such that Ut ∈ L1(Q) for each t. Then the following conditions are equivalent:
(a) U is a Q-supermartingale.
(b) For any stopping time τ, the stopped process Uτ is a Q-supermartingale.
Moreover, in this case we have EQ[ Uτ∧T ]≤ U0 for every stopping time τ.
Proof. If U = M − A is the Doob decomposition of U, then Exercise 6.2.2 implies that U τ = M τ − Aτ is the Doob decomposition of U τ. Since M τ is a martingale by Theorem 6.15 and A is increasing if and only if Aτ is increasing for all stopping times τ, we obtain the equivalence of (a) and (b). Next, if U is a Q-supermartingale, then EQ[ Uτ∧T ]≤ EQ[Mτ∧T ] = M0 = U0, where we have once again used Theorem 6.15 for the martingale M.
Let us return to the problem of finding an optimal exercise time τ for a discounted American claim H. We assume that the buyer chooses the possible exercise times from the set
of all stopping times which do not take the value +∞. Assume that the aim of the buyer is to choose a payoff from the class {Hτ | τ ∈ T } which is optimal in the sense that it has maximal expectation. Thus, the problem is:
The analysis of the optimal stopping problem (6.11) does not require any properties of the underlying market model, not even the absence of arbitrage. We may also drop the positivity assumption on H : All we have to assume is that H is an adapted process which satisfies
This relaxed assumption will be useful in Chapter 9, and it allows us to include the interpretation of the optimal stopping problem in terms of the following utility maximization problem:
Remark 6.17. Suppose the buyer uses a preference relation on X := {Hτ | τ ∈ T } which can be represented in terms of a Savage representation
where Q is a probability measure on (Ω,F), and u is a measurable or continuous function; see Section 2.5. Then a natural goal is to maximize the utility U(Hτ) over all τ ∈ T . This is equivalent to the optimal stopping problem (6.11) for the transformed process 
t := u(Ht), and with respect to the measure Q instead of P. This utility maximization problem is covered by the discussion in this section as long as t ∈ L1(Q) for all t. In Remark 6.50 we will discuss the problem of maximizing the more general utility functionals which appear in a robust Savage representation.
◊
Under the assumption (6.12), we can construct the Snell envelope U := UP of H with respect to P, i.e., U is defined via the recursive formula
Let us define a stopping time τmin by
Note that τmin ≤ T since UT = HT. As we will see in the following theorem, τmin maximizes the expectation of Hτ among all τ ∈ T . In other words, τmin is a solution to our optimal stopping problem (6.11). Similarly, we let
which is a member of the set
The following Theorem uses the essential supremum of a family of random variables as explained in Appendix A.5.
Theorem 6.18. The Snell envelope U of H satisfies
In particular,
Proof. Since U is a supermartingale under P, Corollary 6.16 shows that for τ ∈ Tt
Therefore,
Hence, the theorem will be proved if we can show that 
which is in turn implied by the identity
In order to prove (6.13), let U(t) denote the stopped process
and fix some s between t and T. Then Us > Hs on 
Hence, P-a.s. on 
On the set 
one has 
hence 
Thus, U(t) is a martingale from time t on:
It follows that
This proves the claim (6.13).
Definition 6.19. A stopping time τ∗ ∈ T is called optimal (with respect to P) if
◊
In particular, τmin is an optimal stopping time in the sense of this definition. The following result implies that τmin is in fact the minimal optimal stopping time.
Proposition 6.20. A stopping time τ ∈ T is optimal if and only if Hτ = Uτ P-a.s., and if the stopped process Uτ is a martingale. In particular, any optimal stopping time τ satisfies τ ≥ τmin.
Proof. First note that τ ∈ T is optimal if it satisfies the two conditions of the assertion, because then Theorem 6.18 implies that
For the converse implication, we apply the assumption of optimality, the fact that Hτ ≤ Uτ, and the stopping theorem for supermartingales to obtain that
so that all inequalities are in fact equalities. It follows in particular that Hτ = Uτ P-almost surely. Moreover, the identity E[ Uτ ] = U0 implies that the stopped process Uτ is a supermartingale with constant expectation U0, and hence is a martingale.
In general, there can be many different optimal stopping times. The largest optimal stopping time admits an explicit description: It is the first time before T for which the Snell envelope U loses the martingale property:
Here, A denotes the increasing process obtained from the Doob decomposition of U under P.
Theorem 6.21. A stopping time τ is optimal if and only if P-a.s. τ ≤ τmax and Uτ = Hτ. Moreover, the stopping time τmax is the largest optimal stopping time.
Proof. Let U = M − A be the Doob decomposition of U. Recall from Exercise 6.2.2 that Uτ = Mτ − Aτ is the Doob decomposition of Uτ for any stopping time τ. Thus, Uτ is a martingale if and only if Aτ = 0, because A is increasing. Therefore, Uτ is a martingale if and only if τ ≤ τmax, and so the first part of the assertion follows from Proposition 6.20.
It remains to prove that τmax itself is optimal, i.e., that Uτmax = Hτmax . This is clear on the set {τmax = T}. On the set {τmax = t} for t < T one has At = 0 and At+1 > 0. Hence,
Thus, Ut > E[ Ut+1 | Ft ] and the definition of the Snell envelope yields that Ut = H t ∨ E[ Ut+1 | Ft ] = Ht on {τmax = t}.
Let us now return to our complete financial market model, where H t is the discounted payoff of an American contingent claim. Thus, an optimal stopping strategy for H maximizes the expected payoff E [ Hτ ]. But a stopping time turns out to be the best choice even in a pathwise sense, provided that it is optimal with respect to the unique equivalent martingale measure P∗ in a complete market model. In order to explain this fact, let us first recall from Section 6.1 the construction of a perfect hedge of H from the seller’s perspective. Let
denote the Doob decomposition of the Snell envelope UP∗ of H with respect to P∗. Since P∗ is the unique equivalent martingale measure in our model, the martingale M has the representation
for a d-dimensional predictable process ξ. Clearly, M is equal to the value process of the self-financing strategy constructed from ξ and the initial investment 
Since M dominates H, this yields a perfect hedge of H from the perspective of the seller: If the buyer exercises the option at some stopping time τ, then the seller makes a profit M τ − H τ ≥ 0. The following corollary states that the buyer can in fact meet the value of the seller’s hedging portfolio, and that this happens if and only if the 
option is exercised at an optimal stopping time with respect to P∗. In this sense, can be regarded as the unique arbitrage-free price of the discounted American claim H.
Corollary 6.22. With the above notation,
and equality holds P∗-almost surely if and only if τ is optimal with respect to P∗.
Proof. At time τ,
Moreover, by Theorem 6.21, both 
and Aτ = 0 hold P∗-a.s. if and only if τ is optimal with respect to P∗.
Let us now compare a discounted American claim H to the corresponding discounted European claim H T, i.e., to the contract which is obtained from H by restricting the exercise time to be T. In particular, we are interested in the relation between American and European put or call options. Let
denote the amount needed at time t to hedge H T. Since our market model is complete, Vt can also be regarded as the unique arbitrage-free price of the discounted claim H T at time t. From the seller’s perspective, 
plays a similar role for the American option. It is intuitively clear that an American claim should be more expensive than the corresponding European one. This is made mathematically precise in the following statement.
Proposition 6.23. With the above notation, 
≥ Vt for all t. Moreover, if V dominates H, then UP∗ and V coincide.
Proof. The first statement follows immediately from the supermartingale property of UP∗ :
Next, if the P∗-martingale V dominates H, then it also dominates the corresponding Snell envelope UP∗ by Proposition 6.10. Thus V and UP∗ must coincide. 
Remark 6.24. The situation in which V dominates H occurs, in particular, when the process H is a P∗-submartingale. This happens, for instance, if H is obtained by applying a convex function f : ℝd → [0,∞) to the discounted price process X. Indeed, in this case, Jensen’s inequality for conditional expectations implies that
◊
Example 6.25. The discounted payoff of an American t1call option 
is given by
Under the hypothesis that 
is increasing t0in t, (5.24) states that
In other words, H call is a submartingale, and the Snell envelope UP∗ of H call coincides with the value process
of the corresponding European call option with maturity T. In particular, we have 
= V0, i.e., the unique arbitrage-free price of the American call option is equal to its European counterpart. Moreover, Theorem 6.21 implies that the maximal optimal stopping time with respect to P∗ is given by τmax ≡ T. This suggests that, in a complete model with nonnegative interest rates, an American call should not be exercised before maturity.
◊
Example 6.26. For an American put option 
the situation is different, because the argument in (5.24) fails unless S0 is decreasing. If S0 is increasing and nonconstant, then the time value
of a European put 
typically becomes negative at a certain time t, corresponding to an early exercise premium −Wt; see Figure 5.3. Thus, the early exercise premium is the surplus which an owner of the American put option would have over the value of the European put 
The relation between the price of a put option and its intrinsic value can be illustrated in the context of the CRR model.With the notation of Section 5.5, the price process of the risky asset 
can be written as
and with the constant S0 ≥ 0. Recall that the returns Rk can take only two possible values a and b with −1 < a < b, and that the market model is arbitrage-free if and only if the riskless interest rate r satisfies a < r < b. In this case, the model is complete, and the unique equivalent martingale measure P∗ is characterized by the fact that it makes R1, . . . , RT independent with common distribution
Let
denote the price of Cput regarded as a function of x := S0. Clearly, π(x) is a convex and decreasing function in x. Let us assume that r > 0 and that the parameter a is strictly negative. A trivial situation occurs if the option is “far out of the money” in the sense that
because then St = xΛt ≥ K for all t, and the payoff of Cput is always zero. In particular, π(x) = 0. If
then St = xΛt ≤ K for all t, and hence
In this case, the price of the American put option is equal to its intrinsic value (K − x)+ at time t = 0, and an optimal strategy for the owner would simply consist in exercising the option immediately, i.e., there is no demand for the option in the regime (6.15).
Now consider the case
of a put option which is “at the money” or “not too far out of the money”. For large enough t > 0, the probability 
of a nonzero payoff is strictly positive, while the intrinsic value (K − x)+ vanishes. It follows that the price π(x) is strictly higher than the intrinsic value, and so it is not optimal for the buyer to exercise the option immediately.
Summarizing our observations, we can say that there exists a value x∗ with
such that
see Figure 6.1.
◊
Figure 6.1: The price π(S0) of an American put option as a function of S0 compared to the option’s intrinsic value (K − S0)+.
Remark 6.27. In the context of an arbitrage-free CRR model,we consider a discounted American claim H whose payoff is determined by a function of time and of the current spot price, i.e.,
Clearly, this setting includes American call and put options as special cases. By using the same arguments as in the derivation of (5.29), we get that the Snell envelope UP∗ of H is of the form
where the functions ut are determined by the recursion
Here p∗ is defined as in (6.14), and the parameters â and b are given by â = 1 + a and = 1 + b. Thus, the space [0, T] × [0,∞) can be decomposed into the two regions
and the minimal optimal stopping time τmin can be described as the first exit time of the space time process (t, St) from the continuation region Rc or, equivalently, as the first entrance time into the stopping region Rs:
◊
Exercise 6.2.3. Consider a market model with two assets and an American contingent claim. The development of the discounted price process X := X1 and the discounted American claim is described by the following diagram.
The buyer of the American claim uses a probability measure P that assigns equal probability to each of the possible scenarios. Find an optimal stopping strategy that maximizes E [ Hτ ] over τ ∈ T . What √would be an optimal stopping √time if the buyer uses the utility function u(x) = x and thus aims at maximizing E[Hτ ]? Then show that the market model admits a unique risk-neutral measure P∗ and compute the corresponding Snell envelope UP∗.
◊
Exercise 6.2.4. Let
be the discounted payoff of an American put option with strike K in a market model with one risky asset S = (St)t=0,...T and a riskless asset 
where r > 0. We denote by 
the minimal optimal stopping time of the buyer’s problem to maximize 
over τ ∈ T .
6.3Arbitrage-free prices
In this section, we drop the condition of market completeness, and we develop the notion of an arbitrage-free price π for a discounted American claim H in a general incomplete framework. The basic idea consists in reducing the problem to the determination of the arbitrage-free price for the payoff Hτ which arises from H by fixing the exercise strategy τ. The following remark explains that Hτ can be treated like the discounted payoff of a European contingent claim, whose set of arbitrage-free prices is given by
Remark 6.28. As observed in Remark 5.33, a discounted payoff t which is received at time t < T can be regarded as a discounted European claim E maturing at T. E is obtained from t by investing at time t the payoff 
into the numéraire, i.e., by buying t shares of the 0th asset, and by considering the discounted terminal value of this investment:
In the case of our discounted American claim H which is payed off at the random time τ, we can either apply this argument to each payoff
or directly use a stopping time version of this argument. We conclude that Hτ can be regarded as a discounted European claim, whose arbitrage-free prices are given by (6.16).
◊
Now suppose that H is offered at time t = 0 for a price π ≥ 0. From the buyer’s point of view there should be at least one exercise strategy τ such that the proposed price π is not too high in the sense that π ≤ πʹ for some πʹ ∈ Π(Hτ). From the seller’s point of view the situation looks different: There should be no exercise strategy τʹ such that the proposed price π is too low in the sense that π < πʹ for all πʹ ∈ Π(Hτ). By adding the assumption that the buyer only uses stopping times in exercising the option, we obtain the following formal definition.
Definition 6.29. A real number π is called an arbitrage-free price of a discounted American claim H if the following two conditions are satisfied.
–The price π is not too high in the sense that there exist τ ∈ T and πʹ ∈ Π(Hτ) such that π ≤ πʹ.
–The price π is not too low in the sense that there exists no τʹ ∈ T such that π < πʹ for all πʹ ∈ Π(Hτ).
The set of all arbitrage-free prices of H is denoted Π(H), and we define
◊
Recall from Remark 6.6 that every discounted European claim H E can be regarded as a discounted American claim HA whose payoff is zero if HA is exercised before T, and whose payoff at T equals H E. Clearly, the two sets Π(HE) and Π(HA) coincide, and so the two Definitions 5.28 and 6.29 are consistent with each other.
Remark 6.30. It follows from the definition that any arbitrage-free price π for H must be an arbitrage-free price for some H τ. Hence, (6.16) implies that π = E ∗[ H τ ] for some P∗ ∈ P. The second condition in Definition 6.29 also yields that π ≥ infP∗∈P E∗[ Hτ] for all τʹ ∈ T . It follows that
In particular,
is the unique arbitrage-free price of H if P∗ is the unique equivalent martingale measure in a complete market model, and so Definition 6.29 is consistent with the results of the Section 6.1 and 6.2.
◊
Exercise 6.3.1. Show that in every arbitrage-free market model and for any discounted American claim H,
and that the set Π(H) of arbitrage-free prices is nonempty.
◊
Our main goal in this section is to characterize the set Π(H), and to identify the upper and lower bounds in (6.17) with the quantities πsup(H) and πinf(H). We will work under the simplifying assumption that
For each P∗ ∈ P we denote by UP∗ the corresponding Snell envelope of H, i.e.,
With this notation, the right-hand bound in (6.17) can be written as
In fact, a similar relation also holds for the lower bound in (6.17):
The proof that the above interchange of infimum and supremum is indeed justified under assumption (6.19) is postponed to Section 6.5; see Theorem 6.46. We will now apply it in the following result, which characterizes the set of arbitrage-free prices of a discounted American claim in an arbitrage-free market model that is not necessarily complete.
Theorem 6.31. Under condition (6.19), the set of arbitrage-free prices for H is a real interval with endpoints
and
Moreover, Π(H) either consists of one single point or does not contain its upper endpoint πsup(H).
Proof. Let τ∗ be a stopping time which is optimal with respect to a given P∗ ∈ P. Then 
and consequently 
Together with the a priori bounds (6.17), we obtain the inclusions
where
Moreover, the minimax identity (6.20) shows that
Together with (6.21), this yields the identification of πinf(H) and πsup(H) as a and b.
Now we claim that 
is an interval, which, in view of the preceding step, will prove that Π(H) is also an interval. Take P0, P1 ∈ P and define Pα ∈ P by Pα := αP1 + (1 − α)P0 for 0 ≤ α ≤ 1. By Theorem 6.18, f (α) := 
is the supremum of the affine functions
Thus, f is convex and lower semicontinuous on [0, 1], hence continuous; see part (a) of Proposition A.7. Since P is convex, this proves our claim.
It remains to exclude the possibility that b belongs to Π(H) in case a < b. Suppose by way of contradiction that b ∈ Π(H). Then the first condition in Definition 6.29 implies the existence of Ûτ ∈ T and 
∈ P such that b ≤ 
[ H Ûτ ]. It follows that
In particular, attains the supremum of E ∗[ HÛτ ] over P∗ ∈ P. Theorem 5.32 implies that the discounted European claim HÛτ is attainable and that E∗[ HÛτ ] is in fact independent of P∗ ∈ P. Hence,
and we end up with the contradiction b ≤ a. Thus, b cannot belong to Π(H).
Comparing the previous result with Theorem 5.32, one might wonder whether Π(H) contains its lower bound if πinf(H) < πsup(H). At a first glance, it may come as a surprise that both cases
can occur, as is illustrated by the following simple example.
Example 6.32. Consider the situation of Exercise 5.4.2 in which a complete market model with T = 2 was enlarged by adding two external states ω+ and ω−, corresponding to additional information revealed at time t = 2. That is, the extended model is defined on the probability space ( ÛΩ, Fˆ ,), where ÛΩ := Ω × {ω+, ω−},Fˆ := σ(A × {ω+}| A ∈ F), and 
It was shown in Exercise 5.4.2 that for 0 < p < 1 the probability measure
is an equivalent martingale measure for the enlarged model, where P∗ is the unique equivalent martingale measure in the original, complete model.
Consider the discounted American claim H defined as
Clearly, Π(H) ⊆ [1, 2). On the other hand, τ2 ≡ 2 is an optimal stopping time for
if 
while τ1 ≡ 1 is optimal for 
Hence,
and the lower bound πinf(H) = 1 is an arbitrage-free price for H. Now consider the discounted American claim defined by t = H t for t = 0, 2 and by 1 ≡ 0. In this case, we have
◊
Theorem 6.31 suggests that an American claim H which admits a unique arbitrage-free price should be attainable in an appropriate sense. Corollary 6.22, our hedging result in the case of a complete market, suggests the following definition of attainability.
Definition 6.33. A discounted American claim H is called attainable if there exists a stopping time τ ∈ T and a self-financing trading strategy whose value process V satisfies P-a.s.
The trading strategy is called a hedging strategy for H.
◊
If H is attainable, then a hedging strategy protects the seller not only against those claims Hτ which arise from stopping times τ. The seller is on the safe side even if the buyer has full knowledge of future prices and exercises H at an arbitrary FT-measurable random time σ. For instance, the buyer even could choose σ such that
In fact, we will see in Remark 7.12 that H is attainable in the sense of Definition 6.33 if and only if Vt ≥ H t for all t and Vσ = H σ for some FT-measurable random time σ.
If the market model is complete, then every American claim H is attainable. Moreover, Theorem 6.11 and Corollary 6.22 imply that the minimal initial investment needed for the purchase of a hedging strategy for H is equal to the unique arbitrage-free price of H. In a general market model, every attainable discounted American claim H satisfies our integrability condition (6.19) and has a unique arbitrage-free price which is equal to the initial investment of a hedging strategy for H. This follows from Theorem 5.25. In fact, the following stronger result is true:
Theorem 6.34. For a discounted American claim H satisfying (6.19), the following conditions are equivalent:
(a) H is attainable.
(b) H admits a unique arbitrage-free price π(H), i.e., Π(H) = {π(H)}.
(c) πsup(H) ∈ Π(H).
Moreover, if H is attainable, then π(H) is equal to the initial investment of any hedging strategy for H.
The equivalence of (b) and (c) is an immediate consequence of Theorem 6.31. The remainder of the proof of Theorem 6.34 is postponed to Remark 7.10 because it requires the technique of superhedging, which will be introduced in Section 7.
6.4Stability under pasting
In this section we define the pasting of two equivalent probability measures at a given stopping time. This operation will play an important role in the analysis of lower and upper Snell envelopes as developed in Section 6.5. In particular, we will prepare for the proof of the minimax identity (6.20), which was used in the characterization of arbitrage-free prices of an American contingent claim. Let us start with a few preparations.
Definition 6.35. Let τ be a stopping time. The σ-algebra of events which are observable up to time τ is defined as
◊
Exercise 6.4.1. Prove that Fτ is indeed a σ-algebra. Show next that
and conclude that Fτ coincides with Ft if τ ≡ t. Finally show that Fσ ⊂ Fτ if σ is a stopping time with σ(ω) ≤ τ(ω) for all ω ∈ Ω.
◊
Lemma 6.36. Let τ and σ be two stopping times and suppose that Y isFτ-measurable. Then Y{τ≤σ} and Y{τ<σ} are both Fτ ∩ Fσ-measurable.
Proof. On the one hand, Y{τ≤t} and Y{τ<t} are Ft-measurable, and so
are Ft-measurable for each t. Therefore, Y{τ≤σ} is Fσ-measurable by Exercise 6.4.1. On the other hand, Y{τ=t} is Ft-measurable, {σ ≥ t} = {σ < t}c is Ft−1-measurable, {σ > t} = {σ ≤ t}c is Ft-measurable, and so
are Ft-measurable for each t. It follows again from Exercise 6.4.1 that Y{τ≤σ} is also Fτ-measurable.
The following result is an addendum to Doob’s stopping theorem; see Theorem 6.15:
Proposition 6.37. For an adapted process M in L1(Q) the following conditions are equivalent:
(a) M is a Q-martingale.
(b) EQ[Mτ | Fσ ] = Mτ∧σ for all τ ∈ T and all stopping times σ.
Proof. (a)⇒(b): Take a set A ∈ Fσ and let us write
Condition (b) will follow if we may replace M τ by M σ in the rightmost expectation. To this end, note that
Thus, since the stopped process M τ is a martingale by Theorem 6.15,
(b)⇒(a): This follows by taking τ ≡ t and σ ≡ s ≤ t.
Exercise 6.4.2. Let Z be the density process of a probability measure 
that is absolutely continuous with respect to Q; see Exercise 5.2.3. Show that for a stopping time σ, we have Q on Fσ with density given by
◊
Exercise 6.4.3. Show that for a stopping time τ, a random variable Y ∈ L1(Ω,F, Q), and t ∈ {0, . . . , T},
We next state the following extension of Theorem 6.18. It provides the solution to the optimal stopping problem posed at any stopping time τ ≤ T.
Proposition 6.38. Let H be an adapted process in L1(Ω,F, Q), and define for τ ∈ T
Then the Snell envelope UQ of H satisfies Q-a.s.
and the essential supremum is attained for
Exercise 6.4.4. Prove Proposition 6.38 by using the identity (6.22).
◊
Definition 6.39. Let Q1 and Q2 be two equivalent probability measures and take σ ∈ T . The probability measure
is called the pasting of Q1 and Q2 in σ.
◊
The monotone convergence theorem for conditional expectations guarantees that is indeed a probability measure and that
for all FT-measurable Y ≥ 0. Note that coincides with Q1 on Fσ, i.e.,
Lemma 6.40. For Q1 ≈ Q2, their pasting in σ ∈ T is equivalent to Q1 and satisfies
where Z is the density process of Q2 with respect to Q1.
Proof. For Y ≥ 0,
where we have used the martingale property of Z and the fact that Zσ > 0 Q1-almost surely. The equivalence of and Q1 follows from ZT > 0 Q1-almost surely.
Lemma 6.41. For Q1 ≈ Q2, let be their pasting in σ ∈ T . Then, for all stopping times τ and FT-measurable Y ≥ 0,
Proof. We first show the claimed identity on the set {τ ≤ σ}. To this end, take an Fτ-measurable test function φ ≥ 0. Then φ{τ≤σ} is Fσ ∩Fτ-measurable by Lemma 6.36. Therefore,
It follows that
Next, Exercise 6.4.3 yields that
Moreover, {τ≤σ} is Fτ-measurable by Lemma 6.36. Hence,
Plugging this result into (6.23) shows that our assertion holds on {τ ≤ σ}.
To prove the assertion on {τ > σ}, we show first a preliminary identity. Lemma 6.36 implies that ψ{τ>σ} is Fτ-measurable for any Fσ-measurable ψ. Taking first ψ = 1 and then ψ = 1/Zσ yields that for any FT-measurable W,
After this preparation, we use Proposition A.16 and Lemma 6.40 to obtain that
Using (6.25) with W = 1 on the denominator and with W = Y on the numerator of (6.26) yields
Here, we have used Proposition A.16 in the third identity, the Fτ-measurability of {τ > σ} in the fourth and sixth steps, and (6.24) with reversed roles of τ and σ in the fifth identity.
Definition 6.42. A set Q of equivalent probability measures on (Ω,F) is called stable if, for any Q1, Q2 ∈ Q and σ ∈ T , the pasting in σ is also contained in Q.
◊
The condition of stability in the preceding definition is sometimes also called fork convexity, m-stability, or stability under pasting. For the purposes of this book, the most important example of a stable set is the class P of all equivalent martingale measures. But in Section 6.5 we will also discuss the connection between stable sets and dynamic risk measures.
Proposition 6.43. P is stable.
Proof. Take P1, P2 ∈ P and denote by 
their pasting in a given σ ∈ T . Doob’s stopping theorem in the form of Proposition 6.37 and Lemma 6.41 applied with Y := 
and τ ≡ s yield that for s ≤ t
It follows in particular that each component 
is in L1() since 
< ∞, concluding the proof of ∈ P.
We conclude this section by an alternative characterization of stable sets. It will be used in Section 11.2. Suppose that σ ∈ T takes at most one value t ∈ {0, . . . , T} that is different from T. Then there exists a set B ∈ Ft such that σ = t·B + T·Bc . It follows that the pasting Q of two equivalent probability measures Q1 and Q2 in σ is given by
This observation can be used to give the following characterization of stable sets.
Proposition 6.44. A set Q of equivalent probability measures is stable if and only if for any t ∈ {0, . . . , T} and B ∈ Ft the probability measure defined in (6.27) belongs again to Q.
Proof. We have already seen that ∈ Q if Q is stable. For the proof of the converse implication, let σ ∈ T be a stopping time and take Q1, Q2 ∈ Q. We define recursively T := Q1 and
for t = T, . . . , 1. Then 0 ∈ Q by assumption. We claim that 0 coincides with the pasting of Q1 and Q2 in σ, and this will prove the assertion. To verify our claim, note that the densities of t with respect to Q1 satisfy the recursion
where (Zt) is the density process of Q2 with respect to Q1. But this implies that
and so our claim 0 = follows from Lemma 6.40.
6.5Lower and upper Snell envelopes
Our main goal in this section is to provide a proof of the minimax identity (6.20), that was used in the characterization of the set of arbitrage-free prices of an American contingent claim. The techniques and results which we develop here will help to characterize the time-consistency of dynamic coherent risk measures and they will also be needed in Chapter 7. Moreover, they can be interpreted in terms of an optimal stopping problem for general utility functionals which appear in a robust Savage representation of preferences on payoff profiles. Let us now fix a set Q of equivalent probability measures and an adapted process H such that
Recall that this condition implies
where U Q denotes the Snell envelope of H with respect to Q ∈ Q. Let us also assume that Q is stable.
Definition 6.45. The lower Snell envelope of H is defined as
The upper Snell envelope of H is defined as
◊
We will first study the lower Snell envelope. The following “minimax theorem” states that the essential infimum and the essential supremum occurring in the definition of U↓ may be interchanged if Q is stable. Applied at t = 0 and combined with Proposition 6.43, this gives the identity (6.20), which was used in our characterization of the arbitrage-free prices of H.
Theorem 6.46. The lower Snell envelope of H satisfies
In particular,
The inequality ≥ in (6.28) is obvious. Its converse is an immediate consequence of the next theorem, which solves the following optimal stopping problem that is formulated with respect to the nonadditive expectation operator infQ∈Q EQ[ · ]:
Theorem 6.47. Define a stopping time τt ∈ Tt by
Then, P-a.s.,
In particular,
For the proof of Theorem 6.47, we need some preparations.
Lemma 6.48. Suppose that we are given Q1, Q2 ∈ Q, a stopping time τ ∈ T , and a set B ∈ Fτ. Let ∈ Q be the pasting of Q1 and Q2 in the stopping time
Then the Snell envelopes associated with these three measures are related as follows:
Proof. With Proposition 6.38 and its notation, we have
To compute the conditional expectation on the right, note first that
Hence, Lemma 6.41 yields that
Moreover, whenever ρ1, ρ2 ∈ Tτ, then
is also a stopping time in Tτ. Thus,
and (6.30) follows.
Lemma 6.49. For any Q ∈ Q and τ ∈ T there exist Qk ∈ Q such that Qk = Q on Fτ and
Similarly, there exist Qk ∈ Q such that Qk = Q on Fτ and
Proof. For 
take ∈ Q as in Lemma 6.48. Then
Moreover, if Q1 = Q on Fτ then also = Q on Fτ. Hence, the set
is such that U↓τ = ess inf Φ. Moreover, (6.31) implies that Φ is directed downwards, and the second part of Theorem A.37 states the existence of the desired sequence (Qk) ⊂ Q. The proof for the essential supremum is analogous.
Proof of Theorem 6.47. To prove (6.29), observe first that 
for each Q ∈ Q, so that ≥ holds in (6.29). For the proof of the converse inequality, note that
It was shown in Theorem 6.18 that 
is the minimal optimal stopping time after time t and with respect to Q. It was also shown in the proof of Theorem 6.18 that the stopped process 
is a Q-martingale from time t on. In particular,
Let us now fix some Q ∈ Q. Lemma 6.49 yields Qk ∈ Q with Qk = Q on Fτt such that 
decreases to 
We obtain
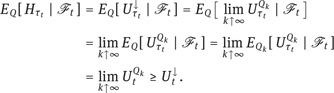
Here we have used that 
together with dominated convergence in the third step, the fact that Qk = Q on Fτt ⊃ Ft in the fourth, and (6.32) in the fifth identity.
Remark 6.50. Suppose the buyer of an American option uses a utility functional of the form
where Q is a set of probability measures and u is a measurable function. This may be viewed as a robust Savage representation of a preference relation on discounted asset payoffs; see Section 2.5. Thus, the aim of the buyer is to maximize the utility
of the discounted payoff Hτ over all stopping times τ ∈ T . This generalized utility maximization problem can be solved with the results developed in this section, provided that the set Q is a stable set of equivalent probability measures. Indeed, assume
and let UQ be the Snell envelope of t with respect to Q ∈ Q. Theorem 6.47 states that the generalized optimal stopping problem is solved by the stopping time
i.e.,
◊
Let us now turn to the analysis of the upper Snell envelope
In order to simplify the presentation, we will assume from now on that
This condition implies that
Our main result on upper Snell envelopes states that, for stable sets Q, the upper Snell envelope U↑ satisfies a recursive scheme that is similar to the one for ordinary Snell envelopes. In contrast to (6.5), however, it involves the nonadditive conditional expectation operators ess supQ E Q[ · |Ft ].
Theorem 6.51. U↑ satisfies the following recursive scheme:
Proof. The definition of the Snell envelope UQ implies that
Next, we fix Q ∈ Q and denote by Qt+1(Q) the set of all ÛQ ∈ Q which coincide with Q on Ft+1. According to Lemma 6.49, there are Qk ∈ Qt+1(Q) such that 
The fact that 
combined with monotone convergence for conditional expectations shows that
In particular, all inequalities are in fact identities. Together with (6.34) we obtain the recursive scheme for U↑.
The following result shows that the nonadditive conditional expectation operators ess supQ EQ[ · |Ft ] associated with a stable set Q enjoy a consistency property that is similar to the martingale property for ordinary conditional expectations.
Theorem 6.52. Let Q be a set of equivalent probability measures and
for some FT-measurable H ≥ 0 such that 
If Q is stable then
Remark 6.53. Note that, for H as in the theorem and τ ∈ T ,
where we have used (6.22) in the second identity.
◊
Proof of Theorem 6.52. By Remark 6.53,
The proof that the right-hand side is equal to ess 
is done by first noting that V↑ is equal to the upper Snell envelope of the process H t given by H T = H and H t = 0 for t < T. Then the same argument as in (6.35) applies. All one has to do is to replace t + 1 by τ.
Remark 6.54. Let us conclude this section by pointing out the connection between stability under pasting and the time-consistency of dynamic coherent risk measures. Let
be a coherent risk measure on L∞(P) defined in terms of a set Qof probability measures equivalent to P. In the context of a dynamic financial market model, it is natural to update the initial risk assessment at later times t > 0. If one continues to use Q as a basis to compute the risk but takes into account the available information, one is led to consider the conditional risk measures
The sequence ρ0 . . . , ρT can be regarded as a dynamic coherent risk measure. Such a dynamic risk measure is called time-consistent or dynamically consistent if
If the set Q in (6.36) is a stable set of equivalent probability measures, then Theorem 6.52 implies immediately the time consistency (6.37). The following converse of this statement, and hence a converse of Theorem 6.52, will be given in Theorem 11.22: if (ρt) is a dynamically consistent sequence of conditional coherent risk measures satisfying certain regularity assumptions, then there exists a stable set Qof equivalent probability measures such that (6.37) holds. An extension of dynamic consistency to dynamic convex risk measures will be given in Section 11.2.
Note that Theorem 6.52 shows that in (6.37) the deterministic times s and t can even be replaced by stopping times if Q is stable.
◊