15

3D Shape Registration Using Spectral Graph Embedding and Probabilistic Matching

Avinash Sharma

INRIA Grenoble Rhône-Alpes

655 avenue de l’Europe

38330 Montbonnot Saint-Martin France

[email protected]

Radu Horaud

INRIA Grenoble Rhône-Alpes

655 avenue de l’Europe

38330 Montbonnot Saint-Martin France

[email protected]

Diana Mateus

Institut für Informatik

Technische Universität Munchen

Garching b. München Germany

[email protected]

CONTENTS

15.1  Introduction

15.2  Graph Matrices

15.2.1  Variants of the Graph Laplacian Matrix

15.3  Spectral Graph Isomorphism

15.3.1  An Exact Spectral Solution

15.3.2  The Hoffman–Wielandt Theorem

15.3.3  Umeyama’s Method

15.4  Graph Embedding and Dimensionality Reduction

15.4.1  Spectral Properties of the Graph Laplacian

15.4.2  Principal Component Analysis of a Graph Embedding

15.4.3  Choosing the Dimension of the Embedding

15.4.4  Unit Hyper-Sphere Normalization

15.5  Spectral Shape Matching

15.5.1  Maximum Subgraph Matching and Point Registration

15.5.2  Aligning Two Embeddings Based on Eigensignatures

15.5.3  An EM Algorithm for Shape Matching

15.6  Experiments and Results

15.7  Discussion

15.8  Appendix: Permutation and Doubly-stochastic Matrices

15.9  Appendix: The Frobenius Norm

15.10  Appendix: Spectral Properties of the Normalized Laplacian

  Bibliography

15.1  Introduction

In this chapter, we discuss the problem of 3D shape matching. Recent advancements in shape acquisition technology has led to the capture of large amounts of 3D data. Existing real-time multi-camera 3D acquisition methods provide a frame-wise reliable visual-hull or mesh representations for real 3D animation sequences [1, 2, 3, 4, 5, 6]. The task of 3D shape analysis involves tracking, recognition, registration, etc. Analyzing 3D data in a single framework is still a challenging task considering the large variability of the data gathered with different acquisition devices. 3D shape registration is one such challenging shape analysis task. The major difficulties in shape registration arise due to: (1) variation in the shape acquisition techniques, (2) local deformations in nonrigid shapes, (3) large acquisition discrepancies (e.g., holes, topology change, surface acquisition noise), (4) local scale change.

Most of the previous attempts of shape matching can be broadly categorized as extrinsic or intrinsic approaches depending on how they analyze the properties of the underlying manifold. Extrinsic approaches mainly focus on finding a global or local rigid transformation between two 3D shapes.

There is a large set of approaches based on variations of the iterative closest point (ICP) algorithm [7, 8, 9] that falls in the category of extrinsic approaches. However, the majority of these approaches compute rigid transformations for shape registration and are not directly applicable to nonrigid shapes. Intrinsic approaches are a natural choice for finding dense correspondences between articulated shapes, as they embed the shape in some canonical domain which preserves some important properties of the manifold, e.g., geodesics and angles. Intrinsic approaches are preferable to extrinsic approaches as they provide a global representation which is invariant to nonrigid deformations that are common in the real-world 3D shapes.

Interestingly, mesh representation also enables the adaptation of well-established graph-matching algorithms that use eigenvalues and eigenvectors of graph matrices, and are theoretically well investigated in the framework of spectral graph theory (SGT), e.g., [10, 11]. Existing methods in SGT are mainly theoretical results applied to small graphs and under the premise that eigenvalues can be computed exactly. However, spectral graph matching does not easily generalize to very large graphs due to the following reasons: (1) eigenvalues are approximately computed using eigen-solvers, (2) eigenvalue multiplicity and hence ordering change are not well studied, and (3) exact matching is intractable for very large graphs. It is important to note that these methods mainly focus on exact graph matching, while the majority of the real-world graph matching applications involve graphs with different cardinality and for which only a subgraph isomorphism can be sought.

The main contribution of this work is to extend the spectral graph methods to very large graphs by combining spectral graph matching with Laplacian embedding. Since the embedded representation of a graph is obtained by dimensionality reduction, we claim that the existing SGT methods (e.g., [10]) are not easily applicable. The major contributions of this work are the following: (1) we discuss solutions for the exact and inexact graph isomorphism problems and recall the main spectral properties of the combinatorial graph Laplacian, (2) we provide a novel analysis of the commute-time embedding that allows us to interpret the latter in terms of the PCA of a graph, and to select the appropriate dimension of the associated embedded metric space, (3) we derive a unit hyper-sphere normalization for the commute-time embedding that allows us to register two shapes with different samplings, (4) we propose a novel method to find the eigenvalue-eigenvector ordering and the eigenvector signs using the eigensignatures (histograms) that are invariant to the isometric shape deformations and which fits well in the spectral graph matching framework, and (5) we present a probabilistic shape matching formulation using an expectation maximization (EM) framework for implementing a point registration algorithm which alternates between aligning the eigenbases and finding a vertex-to-vertex assignment.

The existing graph-matching methods that use intrinsic representations are [12, 13, 14, 15, 16, 17, 18, 19]. There is another class of methods that allows intrinsic (geodesics) and extrinsic (appearance) features to be combined and which were previously successfully applied for matching features in pairs of images [20, 21, 22, 23, 24, 25, 26, 27, 28, 29]. Some recent approaches apply hierarchical matching to find dense correspondences [30, 31, 32]. However, many of these graph-matching algorithms suffer from the problem of either computational intractability or a lack of a proper metric as the Euclidean metric is not directly applicable while computing distances on nonrigid shapes. A recent benchmarking of shape-matching methods was performed in [33]. Recently, a few methods proposed a diffusion framework for the task of shape registration [34, 35, 36].

In this chapter, we present an intrinsic approach for unsupervised 3D shape registration first proposed in [16, 37]. In the first step, dimensionality reduction is performed using the graph Laplacian, which allows us to embed a 3D shape in an isometric subspace invariant to nonrigid deformations. This leads to an embedded point cloud representation where each vertex of the underlying graph is mapped to a point in a K-dimensional metric space. Thus, the problem of nonrigid 3D shape registration is transformed into a K-dimensional point registration task. However, before point registration, the two eigen spaces need to be correctly aligned. This alignment is critical for the spectral matching methods because the two eigen spaces are defined up to the signs and the ordering of the eigenvectors of their Laplacian matrices. This is achieved by a novel matching method that uses histograms of eigenvectors as eigensignatures. In the final step, a point registration method based on a variant of the expectation-maximization (EM) algorithm [38] is applied in order to register two sets of points associated with the Laplacian embeddings of the two shapes. The proposed algorithm alternates between the estimation of an orthogonal transformation matrix associated with the alignment of the two eigen spaces and the computation of probabilistic vertex-to-vertex assignment. Figure 15.1 presents an overview of the proposed method. According to the results summarized in [33], this method is one among the best-performing unsupervised shape-matching algorithms.

FIGURE 15.1
Overview of the proposed method. First, a Laplacian embedding is obtained for each shape. Next, these embeddings are aligned to handle the issue of sign flip and ordering change using the histogram matching. Finally, an Expectation-Maximization based point registration is performed to obtain dense probabilistic matching between two shapes.

Chapter Overview

Graph matrices are introduced in Section 15.2. The problem of exact graph isomorphism and existing solutions are discussed in Section 15.3. Section 15.4 deals with dimensionality reduction using the graph Laplacian in order to obtain embedded representations for 3D shapes. In the same section, we discuss the PCA of graph embeddings and propose a unit hyper-sphere normalization for these embeddings along with a method to choose the embedding dimension. Section 15.5 introduces the formulation of maximum subgraph isomorphism before presenting a two-step method for 3D shape registration. In the first step, Laplacian embeddings are aligned using histogram matching, while in the second step we briefly discuss an EM point registration method to obtain probabilistic shape registration. Finally, we present shape-matching results in Section 15.6 and conclude with a brief discussion in Section 15.7.

15.2  Graph Matrices

A shape can be treated as a connected undirected weighted graph g = {V, ℰ}$g=\left\{\mathcal{V},ℰ\right\}$, where $\mathcal{V}\left(g\right)=\left\{{\upsilon }_1,\mathrm{\dots },{\upsilon }_n\right\}$ is the vertex set, and $ℰ\left(g\right)=\left\{e_{ij}\right\}$ is the edge set. Let W be the weighted adjacency matrix of this graph. Each (i, j)^th entry of W matrix stores weight w_ij whenever there is an edge e_ij ∈ ϵ(g) between graph vertices υ_i and υ_j and 0 otherwise with all the diagonal elements set to 0. We use the following notations: The degree d_i of a graph vertex $d_i={\displaystyle {\sum }_{i~j}{w}_{ij}}$ (i ~ j denotes the set of vertices υ_j that are adjacent to υ_i), the degree matrix D = diag[d₁ … d _i … d_n], the n × 1 vector $1={\left(1\mathrm{\dots }1\right)}^{┬}$ (the constant vector), the n × 1 degree vector $d=D1$, and the graph volume $\text{Vol}\left(g\right)={\displaystyle {\sum }_i{d}_i}$.

In spectral graph theory, it is common [39, 40] to use the following expression for the edge weights:

$w_{ij}=e^{-\frac{{\text{dist}}^2\left({\upsilon }_i,{\upsilon }_j\right)}{{\sigma }^2}},$

(15.1)

where dist(υ_i, υ_j) denotes any distance metric between two vertices and σ is a free parameter. In the case of a fully connected graph, matrix W is also referred to as the similarity matrix. The normalized weighted adjacency matrix writes $\tilde{W}=D^{-1/2}W{D}^{-1/2}$. The transition matrix of the nonsymmetric reversible Markov chain associated with the graph is ${\tilde{W}}_R=D^{-1}W=D^{-1/2}\tilde{W}{D}^{1/2}$.

15.2.1  Variants of the Graph Laplacian Matrix

We can now build the concept of the graph Laplacian operator. We consider the following variants of the Laplacian matrix [41, 40, 42]:

•  The unnormalized Laplacian, which is also referred to as the combinatorial Laplacian L,

•  The normalized Laplacian $\tilde{L}$, and

•  The random-walk Laplacian ${\tilde{L}}_R$ also referred to as the discrete Laplace operator.

In more detail, we have:

$L=D-W$

(15.2)

$\tilde{L}=D^{-1/2}L{D}^{-1/2}=I-\tilde{W}$

(15.3)

${\tilde{L}}_R=D^{-1}L=I-{\tilde{W}}_R$

(15.4)

with the following relations between these matrices:

$L=D^{1/2}\tilde{L}{D}^{1/2}=D{\tilde{L}}_R$

(15.5)

$\tilde{L}=D^{-1/2}L{D}^{-1/2}=D^{1/2}{\tilde{L}}_R{D}^{-1/2}$

(15.6)

${\tilde{L}}_R=D^{-1/2}\tilde{L}{D}^{-1/2}=D^{-1}L.$

(15.7)

15.3  Spectral Graph Isomorphism

Let g_A and g_B be two undirected weighted graphs with the same number of nodes, n, and let W_A and W_B be their adjacency matrices. They are real-symmetric matrices. In the general case, the number r of distinct eigenvalues of these matrices is smaller than n. The standard spectral methods only apply to those graphs whose adjacency matrices have n distinct eigenvalues (each eigenvalue has multiplicity one), which implies that the eigenvalues can be ordered.

Graph isomorphism [43] can be written as the following minimization problem:

$P^{\star }=\arg \underset{P}{\min }{\Vert W_A-P{W}_B{P}^{\text{⊤}}\Vert }_F^2$

(15.8)

where P is an n × n permutation matrix (see appendix 15.8) with P^⋆ as the desired vertex-to-vertex permutation matrix and ║•║_F is the Frobenius norm defined by (see Appendix 15.9):

${\Vert W\Vert }_F^2=\langle W,W\rangle ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{w}_{ij}^2}=\text{tr}\left(W^{\text{⊤}}W\right)}$

(15.9)

Let:

$W_A=U_A{\Lambda }_A{U}_A^{\top }$

(15.10)

$W_B=U_B{\Lambda }_B{U}_B^{\top }$

(15.11)

be the eigen-decompositions of the two matrices with n eigenvalues Λ_A = diag [α_i] and Λ_B = diag[β_i] and n orthonormal eigenvectors, the column vectors of U_A and U_B.

15.3.1  An Exact Spectral Solution

If there exists a vertex-to-vertex correspondence that makes (15.8) equal to 0, we have

$W_A=P^{\star }{W}_B{P}^{\star }{}^{\top }.$

(15.12)

This implies that the adjacency matrices of the two graphs should have the same eigenvalues. Moreover, if the eigenvalues are non-null and, the matrices U_A and U_B have full rank and are uniquely defined by their n orthonormal column vectors (which are the eigenvectors of W_A and W_B), then α_i = β_i, ∀i, 1 ≤ i ≤ n and Λ_A = Λ_B. From (15.12) and using the eigen-decompositions of the two graph matrices, we obtain

${\Lambda }_A=U_A^{\top }{P}^{\star }{\stackrel{⌣}{U}}_B{\Lambda }_B{\stackrel{⌣}{U}}_B^{\top }{P}^{\star }{}^{\top }{U}_A={\Lambda }_B,$

(15.13)

where the matrix ${\stackrel{⌣}{U}}_B$ is defined by

${\stackrel{⌣}{U}}_B=U_{B}S.$

(15.14)

Matrix S = diag[s_i], with s_i = ±1, is referred to as a sign matrix with the property S² = I. Post multiplication of U_B with a sign matrix takes into account the fact that the eigenvectors (the column vectors of U_B) are only defined up to a sign. Finally, we obtain the following permutation matrix:

$P^{\star }=U_{B}S{U}_A^{\top }.$

(15.15)

Therefore, one may notice that there are as many solutions as the cardinality of the set of matrices S_n, i.e., |S_n| = 2ⁿ, and that not all of these solutions correspond to a permutation matrix. This means that there exist some matrices S^⋆ that exactly make P^⋆ a permutation matrix. Hence, all those permutation matrices that satisfy (15.15) are solutions of the exact graph isomorphism problem. Notice that once the permutation has been estimated, one can write that the rows of U_B can be aligned with the rows of U_A:

$U_A=P^{\star }{U}_B{S}^{\star }.$

(15.16)

The rows of U_A and of U_B can be interpreted as isometric embeddings of the two graph vertices: A vertex υ_i of g_A has as coordinates the i^th row of U_A. This means that the spectral graph isomorphism problem becomes a point registration problem, where graph vertices are represented by points in ${ℝ}^n$. To conclude, the exact graph isomorphism problem has a spectral solution based on (i) the eigen-decomposition of the two graph matrices, (ii) the ordering of their eigenvalues, and (iii) the choice of a sign for each eigenvector.

15.3.2  The Hoffman–Wielandt Theorem

The Hoffman–Wielandt theorem [44, 45] is the fundamental building block of spectral graph isomorphism. The theorem holds for normal matrices; Here, we restrict the analysis to real symmetric matrices, although the generalization to Hermitian matrices is straightforward.

Theorem 15.3.1

(Hoffman and Wielandt) If W_A and W_B are real-symmetric matrices, and if α_i and β_i are their eigenvalues arranged in increasing order, α₁ ≤ … ≤ α_i ≤ … ≤ α_n and β₁ ≤ … ≤ β_i ≤ … ≤ β_n, then

${\displaystyle \sum _{i=1}^n{\left({\alpha }_i-{\beta }_i\right)}^2\le {\Vert W_A-W_B\Vert }_F^2.}$

(15.17)

Proof: The proof is derived from [11, 46]. Consider the eigen-decompositions of matrices W_A and W_B, (15.10), (15.11). Notice that for the time being we are free to prescribe the ordering of the eigenvalues α_i and β_i and hence the ordering of the column vectors of matrices U_A and U_B. By combining (15.10) and (15.11), we write:

$U_A{\Lambda }_A{U}_A^{\top }-U_B{\Lambda }_B{U}_B^{\top }=W_A-W_B$

(15.18)

or, equivalently

${\Lambda }_A{U}_A^{\top }{U}_B-U_A^{\top }{U}_B{\Lambda }_B=U_A^{\top }\left(W_A-W_B\right)U_B.$

(15.19)

By the unitary-invariance of the Frobenius norm (see Appendix 15.9) and with the notation $Z=U_A^{\top }{U}_B$ we obtain

${\Vert {\Lambda }_{A}Z-Z{\Lambda }_B\Vert }_F^2={\Vert W_A-W_B\Vert }_F^2,$

(15.20)

which is equivalent to

${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\left({\alpha }_i-{\beta }_j\right)}^2{z}_{ij}^2={\Vert W_A-W_B\Vert }_F^2.}}$

(15.21)

The coefficients $x_{ij}=z_{ij}^2$ can be viewed as the entries of a doubly-stochastic matrix $X:x_{ij}\ge 0,{\displaystyle {\sum }_{i=1}^n{x}_{ij}=1,{\displaystyle {\sum }_{j=1}^n{x}_{ij}=1}}$. Using these properties, we obtain

$\begin{array}{c}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\left({\alpha }_i-{\beta }_j\right)}^2{z}_{ij}^2={\displaystyle {\sum }_{i=1}^n{\alpha }_i^2+{\displaystyle {\sum }_{j=1}^n{\beta }_j^2-2{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{z}_{ij}^2{\alpha }_i{\beta }_j}}}}}}\\ \ge {\displaystyle \sum _{i=1}^n{\alpha }_i^2+{\displaystyle \sum _{j=1}^n{\beta }_j^2}-2{\max }_Z\left\{{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{z}_{ij}^2{\alpha }_i{\beta }_j}}\right\}.}\end{array}$

(15.22)

Hence, the minimization of (15.21) is equivalent to the maximization of the last term in (15.22). We can modify our maximization problem to admit all the doubly-stochastic matrices. In this way we seek an extremum over a convex compact set. The maximum over this compact set is larger than or equal to our maximum:

$\underset{Z\in {\mathcal{O}}_n}{\max }\left\{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{z}_{ij}^2{\alpha }_i{\beta }_j}}\right\}\le \underset{X\in {\mathcal{D}}_n}{\max }\left\{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_{ij}{\alpha }_i{\beta }_j}}\right\}$

(15.23)

where ${\mathcal{O}}_n$ is the set of orthogonal matrices and ${\mathcal{D}}_n$ is the set of doubly stochastic matrices (see Appendix 15.8). Let c_ij = α_ijβ_j and hence one can write that the right term in the equation above as the dot-product of two matrices:

$\langle X,C\rangle =\text{tr}\left(XC\right)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_{ij}{c}_{ij}.}}$

(15.24)

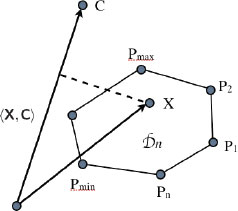
Therefore, this expression can be interpreted as the projection of X onto C; see Figure 15.2. The Birkhoff theorem (Appendix 15.8) tells us that the set ${\mathcal{D}}_n$ of doubly stochastic matrices is a compact convex set. We obtain that the extrema (minimum and maximum) of the projection of X onto C occur at the projections of one of the extreme points of this convex set, which correspond to permutation matrices. Hence, the maximum of 〈X, C〉 is 〈P_max, X〉, and we obtain

FIGURE 15.2
This figure illustrates the maximization of the dot-product 〈X, C〉. The two matrices can be viewed as vectors of dimension n². Matrix X belongs to a compact convex set whose extreme points are the permutation matrices P₁, P₂,…, P_n. Therefore, the projection of this set (i.e., ${\mathcal{D}}_n$) onto C has projected permutation matrices at its extremes, namely 〈P_min, X〉 and 〈P_max, X〉 in this example.

$\underset{X\in {\mathcal{D}}_n}{\max }\left\{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_{ij}{\alpha }_i{\beta }_j}}\right\}={\displaystyle \sum _{i=1}^n{\alpha }_i{\beta }_{\pi \left(i\right)}.}$

(15.25)

By substitution in (15.22) we obtain

${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\left({\alpha }_i-{\beta }_j\right)}^2{z}_{ij}^2\ge {\displaystyle \sum _{i=1}^n{\left({\alpha }_i-{\beta }_{\pi \left(i\right)}\right)}^2.}}}$

(15.26)

If the eigenvalues are in increasing order, then the permutation that satisfies Theorem 15.17 is the identity matrix, i.e., π(i) = i. Indeed, let’s assume that for some indices k and k + 1 we have π(k) = k + 1 and π(k + 1) = k. Since α_k ≤ α_k+1 and β_k ≤ β_k+1, the following inequality holds:

${\left({\alpha }_k-{\beta }_k\right)}^2+{\left({\alpha }_{k+1}-{\beta }_{k+1}\right)}^2\le {\left({\alpha }_k-{\beta }_{k+1}\right)}^2+{\left({\alpha }_{k+1}-{\beta }_k\right)}^2$

(15.27)

and hence (15.17) holds.

Corollary 15.3.2

The inequality (15.17) becomes an equality when the eigenvectors of W_A are aligned with the eigenvectors of W_B up to a sign ambiguity:

$U_B=U_{A}S.$

(15.28)

Proof: Since the minimum of (15.21) is achieved for X = I and since the entries of X are $z_{ij}^2$, we have that z_ii = ±1, which corresponds to Z = S.

Corollary 15.3.3

If Q is an orthogonal matrix, then

${\displaystyle \sum _{i=1}^n{\left({\alpha }_i-{\beta }_i\right)}^2\le {\Vert W_A-Q{W}_B{Q}^{\top }\Vert }_F^2}.$

(15.29)

Proof: Since the eigen-decomposition of matrix QW_BQ^⊤ is (QU_B)Λ_B (QU_B)^⊤ and since it has the same eigenvalues as W_B, the inequality (15.29) holds and hence Corollary 15.3.3.

These corollaries will be useful in the case of spectral graph-matching methods presented below.

15.3.3  Umeyama’s Method

The exact spectral matching solution presented in section 15.3.1 finds a permutation matrix satisfying (15.15). This requires an exhaustive search over the space of all possible 2ⁿ matrices. Umeyama’s method presented in [10] proposes a relaxed solution to this problem as outlined below.

Umeyama [10] addresses the problem of weighted graph matching within the framework of spectral graph theory. He proposes two methods, the first for undirected weighted graphs and the second for directed weighted graphs. The adjacency matrix is used in both cases. Let’s consider the case of undirected graphs. The eigenvalues are (possibly with multiplicities):

$W_A:{\alpha }_1\le \mathrm{\dots }\le {\alpha }_i\le \mathrm{\dots }\le {\alpha }_n$

(15.30)

$W_B:{\beta }_1\le \mathrm{\dots }\le {\beta }_i\le \mathrm{\dots }\le {\beta }_n.$

(15.31)

Theorem 15.3.4

(Umeyama) If W_A and W_B are real-symmetric matrices with n distinct eigenvalues (that can be ordered), α₁ < … < α_i < … < α_n and β₁ < … < β_i < … < β_n, the minimum of

$J\left(Q\right)={\Vert W_A-Q{W}_B{Q}^{\top }\Vert }_F^2$

(15.32)

is achieved for

$Q^{\star }=U_{A}S{U}_B^{\top }$

(15.33)

and hence (15.29) becomes an equality:

${\displaystyle \sum _{i=1}^n{\left({\alpha }_i-{\beta }_i\right)}^2}={\Vert W_A-Q^{\star }{W}_B{Q}^{\star \top }\Vert }_F^2.$

(15.34)

Proof: The proof is straightforward. By corollary 15.3.3, the Hoffman–Wielandt theorem applies to matrices W_A and QW_BQ^⊤. By Corollary 15.3.2, the equality (15.34) is achieved for

$Z=U_A^{\top }{Q}^{\star }{U}_B=S$

(15.35)

and hence (15.33) holds. ▮

Notice that (15.33) can be written as

$U_A=Q^{\star }{U}_{B}S$

(15.36)

which is a relaxed version of (15.16): The permutation matrix in the exact isomorphism case is replaced by an orthogonal matrix.

A Heuristic for Spectral Graph Matching

Let us consider again the exact solution outlined in Section 15.3.1. Umeyama suggests a heuristic in order to avoid exhaustive search over all possible 2ⁿ matrices that satisfy (15.15). One may easily notice that

${\Vert P-U_{A}S{U}_B^{\top }\Vert }_F^2=2n-2\text{tr}\left(U_{A}S{\left(P{U}_B\right)}^{\top }\right).$

(15.37)

Using Umeyama’s notations, ${\overline{U}}_A=\left[\left|u_{ij}\right|\right]$, ${\overline{U}}_B=\left[\left|{\upsilon }_{ij}\right|\right]$ (the entries of ${\overline{U}}_A$ are the absolute values of the entries of U_A), one may further notice that

$\text{tr}\left(U_{A}S{\left(P{U}_B\right)}^{\top }\right)={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{s}_j{u}_{ij}{\upsilon }_{\pi \left(i\right)j}\le {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\left|u_{ij}\right|\left|{\upsilon }_{\pi \left(i\right)j}\right|=\text{tr}\left({\overline{U}}_A{\overline{U}}_B^{\top }{P}^{\top }\right).}}}}$

(15.38)

The minimization of (15.37) is equivalent to the maximization of (15.38) and the maximal value that can be attained by the latter is n. Using the fact that both U_A and U_B are orthogonal matrices, one can easily conclude that

$\text{tr}\left({\overline{U}}_A{\overline{U}}_B^{\top }{P}^{\top }\right)\le n.$

(15.39)

Umeyama concludes that when the two graphs are isomorphic, the optimum permutation matrix maximizes $\text{tr}\left({\overline{U}}_A{\overline{U}}_B^{\top }{P}^{\top }\right)$, and this can be solved by the Hungarian algorithm [47].

When the two graphs are not exactly isomorphic, theorems 15.3.1 and 15.3.4 allow us to relax the permutation matrices to the group of orthogonal matrices. Therefore, with similar arguments as above, we obtain

$\text{tr}\left(U_{A}S{U}_B^{\top }{Q}^{\top }\right)\le \text{tr}\left({\overline{U}}_A{\overline{U}}_B^{\top }{Q}^{\top }\right)\le n.$

(15.40)

The permutation matrix obtained with the Hungarian algorithm can be used as an initial solution that can then be improved by some hill-climbing or relaxation technique [10].

The spectral matching solution presented in this section is not directly applicable to large graphs. In the next section, we introduce the notion of dimensionality reduction for graphs, which will lead to a tractable graph-matching solution.

15.4  Graph Embedding and Dimensionality Reduction

For large and sparse graphs, the results of Section 15.3 and Umeyama’s method (Section 15.3.3) hold only weakly. Indeed, one cannot guarantee that all the eigenvalues have multiplicity equal to one: the presence of symmetries causes some of eigenvalues to have an algebraic multiplicity greater than one. Under these circumstances and due to numerical approximations, it might not be possible to properly order the eigenvalues. Moreover, for very large graphs with thousands of vertices it is not practical to compute all its eigenvalue–eigenvector pairs. This means that one has to devise a method that is able to match shapes using a small set of eigenvalues and eigenvectors.

One elegant way to overcome this problem, is to reduce the dimension of the eigenspace, along the line of spectral dimensionality reduction techniques. The eigen-decomposition of graph Laplacian matrices (introduced in Section 15.2.1) is a popular choice for the purpose of dimensionality reduction [39].

15.4.1  Spectral Properties of the Graph Laplacian

The spectral properties of the Laplacian matrices introduced in Section 15.2.1 have been thoroughly studied. They are summarized in table 15.1. We derive some subtle properties of the combinatorial Laplacian that will be useful for the task of shape registration. In particular, we will show that the eigenvectors of the combinatorial Laplacian can be interpreted as directions of maximum variance (principal components) of the associated embedded shape representation. We note that the embeddings of the normalized and random-walk Laplacians have different spectral properties which make them less interesting for shape registration, i.e., Appendix 15.10.

Laplacian	Null space	Eigenvalues	Eigenvectors
L = UΛU⊤	$u_1=1$	0 = λ1 < λ2 ≤ … ≤ λn	$u_{i>1}^{\top }1=0$ $u_i^{\top }{u}_j={\delta }_{ij}$
$\tilde{L}=\tilde{U}\Gamma {\tilde{U}}^{\top }$	${\tilde{u}}_1=D^{1/2}1$	0 = γ1 < γ2 ≤ … ≤ γn	${\tilde{u}}_{i>1}^{\top }{D}^{1/2}1=0$ ${\tilde{u}}_i^{\top }{\tilde{u}}_j={\delta }_{ij}$
${\tilde{L}}_R=T\Gamma T^{-1},T=D^{-1/2}\tilde{U}$	$t_1=1$	0 = γ1 < γ2 ≤ … ≤ γn	$t_{i>1}^{\top }D1=0,t_i^{\top }D{t}_j={\delta }_{ij}$

TABLE 15.1
Summary of the spectral properties of the Laplacian matrices. Assuming a connected graph, the null eigenvalue (λ₁, γ₁) has multiplicity one. The first non-null eigenvalue (λ₂, γ₂) is known as the Fiedler value, and its multiplicity is, in general, equal to one. The associated eigenvector is denoted the Fiedler vector [41].

The combinatorial Laplacian.

Let L = UΛU^⊤ be the spectral decomposition of the combinatorial Laplacian with UU^⊤ = I. Let U be written as

$U=\left[\begin{array}{ccccc}{u}_{11}& \cdots & u_{1k}& \cdots & u_{1n}\\ ⋮& & ⋮& & ⋮\\ u_{n1}& \mathrm{\dots }& u_{nk}& \mathrm{\dots }& u_{nn}\end{array}\right]$

(15.41)

Each column of U, u_k = (u_1k … u_ik … u_nk)^⊤ is an eigenvector associated with the eigenvalue λ_k. From the definition of L in (15.2) (see [39]), one can easily see that λ₁ = 0 and that $u_1=1$ (a constant vector). Hence, $u_{k\ge 2}^{\top }1=0$ and by combining this with $u_k^{\top }{u}_k=1$, we derive the following proposition.

Proposition 15.4.1

The components of the nonconstant eigenvectors of the combinatorial Laplacian satisfy the following constraints:

${\displaystyle {\sum }_{i=1}^n{u}_{ik}=0,\forall k,2\le k\le n}$

(15.42)

$-1<u_{ik}<1,\forall i,k,1\le i\le n,2\le k\le n.$

(15.43)

Assuming a connected graph, λ₁ has multiplicity equal to one [40]. Let’s organize the eigenvalues of L in increasing order: 0 = λ₁ < λ₂ ≤ … ≤ λ_n. We prove the following proposition [41].

Proposition 15.4.2

For all k ≤ n, we have λ_k ≤ 2 max_i(d_i), where d_i is the degree of vertex i.

Proof: The largest eigenvalue of L corresponds to the maximization of the Rayleigh quotient, or

${\lambda }_n=\underset{u}{\max }\frac{u^{\top }Lu}{u^{\top }u}.$

(15.44)

We have $u^{\top }Lu={{\displaystyle {\sum }_{e_{ij}}{w}_{ij}\left(u_i-u_j\right)}}^2$. From the inequality (a − b)² ≤ 2(a² + b²) we obtain

${\lambda }_n\le \frac{2{\displaystyle {\sum }_{e_{ij}}{w}_{ij}\left(u_i^2+u_j^2\right)}}{{\displaystyle {\sum }_i{u}_i^2}}=\frac{2{\displaystyle {\sum }_i{d}_i{u}_i^2}}{{\displaystyle {\sum }_i{u}_i^2}}\le 2\underset{i}{\max }\left(d_i\right).$

(15.45)

This ensures an upper limit on the eigenvalues of L. By omitting the zero eigenvalue and associated eigenvector, we can rewrite L as

$L={\displaystyle \sum _{k=2}^n{\lambda }_k{u}_k{u}_k^{\top }.}$

(15.46)

Each entry u_ik of an eigenvector u_k can be interpreted as a real-valued function that projects a graph vertex υ_i onto that vector. The mean and variance of the set ${\left\{u_{ik}\right\}}_{i=1}^n$ are therefore a measure of how the graph spreads when projected onto the k-th eigenvector. This is clarified by the following result.

Proposition 15.4.3

The mean ${\overline{u}}_k$ and the variance σ_uk of an eigenvector u_k. For 2 ≤ k ≤ n, and 1 ≤ i ≤ n we have

${\overline{u}}_k={\displaystyle \sum _{i=1}^n{u}_{ik}=0}$

(15.47)

${\sigma }_{u_k}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(u_{ik}-{\overline{u}}_k\right)}^2}=\frac{1}{n}$

(15.48)

Proof: These results can be easily obtained from $u_{k\ge 2}^{\top }1=0$ and $u_k^{\top }{u}_k=1$. ▮

These properties will be useful while aligning two Laplacian embeddings and thus registering two 3D shapes.

15.4.2  Principal Component Analysis of a Graph Embedding

The Moore–Penrose pseudo-inverse of the Laplacian can be written as

$\begin{array}{ll}{L}^{†}\hfill & =U{\Lambda }^{-1}{U}^{\top }\hfill \\ \hfill & ={\left({\Lambda }^{-\frac{1}{2}}{U}^{\top }\right)}^{\top }\left({\Lambda }^{-\frac{1}{2}}{U}^{\top }\right)\hfill \\ \hfill & =X^{\top }X\hfill \end{array}$

(15.49)

where Λ⁻¹ = diag(0, 1/λ₂,…, 1/λ_n).

The symmetric semi-definite positive matrix L^† is a Gram matrix with the same eigenvectors as those of the graph Laplacian. When omitting the null eigenvalue and associated constant eigenvector, X becomes a (n − 1) × n matrix whose columns are the coordinates of the graph’s vertices in an embedded (or feature) space, i.e., X = [x₁ … x_j … x_n]. It is interesting to note that the entries of L^† may be viewed as kernel dot-products, or a Gram matrix [48]. The Gram-matrix representation allows us to embed the graph in an Euclidean feature-space where each vertex υ_j of the graph is a feature point represented as x_j.

The left pseudo-inverse operator of the Laplacian L, satisfying L^†Lu = u for any u┴null(L), is also called the Green function of the heat equation. Under the assumption that the graph is connected and thus L has an eigenvalue λ₁ = 0 with multiplicity 1, we obtain

$L^{†}={\displaystyle \sum _{k=2}^n\frac{1}{{\lambda }_k}{u}_k{u}_k^{\top }.}$

(15.50)

The Green function is intimately related to random walks on graphs, and can be interpreted probabilistically as follows. Given a Markov chain such that each graph vertex is the state, and the transition from vertex υ_i is possible to any adjacent vertex υ_j ~ υ_i with probability w_ij/d_i, the expected number of steps required to reach vertex υ_j from υ_i, called the access or hitting time O(υ_i, υ_j). The expected number of steps in a round trip from υ_i to υ_j is called the commute-time distance: CTD²(υ_i, υ_j) = O(υ_i, υ_j) + O(υ_j, υ_i). The commute-time distance [49] can be expressed in terms of the entries of L^†:

$\begin{array}{ll}{\text{CTD}}^2\left({\upsilon }_i,{\upsilon }_j\right)\hfill & =\text{Vol}\left(g\right)\left(L^{†}\left(i,i\right)+L^{†}\left(j,j\right)-2L^{†}\left(i,j\right)\right)\hfill \\ \hfill & =\text{Vol}\left(g\right)\left({\displaystyle \sum _{k=2}^n\frac{1}{{\lambda }_k}{u}_{ik}^2+{\displaystyle \sum _{k=2}^n\frac{1}{{\lambda }_k}{u}_{jk}^2-2{\displaystyle \sum _{k=2}^n\frac{1}{{\lambda }_k}{u}_{ik}{u}_{jk}}}}\right)\hfill \\ \hfill & =\text{Vol}\left(g\right){\displaystyle \sum _{k=2}^n{\left({\lambda }_k^{-1/2}\left(u_{ik}-u_{jk}\right)\right)}^2}\hfill \\ \hfill & =\text{Vol}\left(g\right){\Vert x_i-x_j\Vert }^2,\hfill \end{array}$

(15.51)

where the volume of the graph, Vol(g) is the sum of the degrees of all the graph vertices. The CTD function is positive-definite and sub-additive, thus defining a metric between the graph vertices, referred to as commute-time (or resistance) distance [50]. The CTD is inversely related to the number and length of paths connecting two vertices. Unlike the shortest-path (geodesic) distance, CTD captures the connectivity structure of the graph volume rather than a single path between the two vertices. The great advantage of the commute-time distance over the shortest geodesic path is that it is robust to topological changes and therefore is well suited for characterizing complex shapes. Since the volume is a graph constant, we obtain

${\text{CTD}}^2\left({\upsilon }_i,{\upsilon }_j\right)\propto {\Vert x_i-x_j\Vert }^2.$

(15.52)

Hence, the Euclidean distance between any two feature points x_i and x_j is the commute time distance between the graph vertex υ_i and υ_j.

Using the first K non-null eigenvalue–eigenvector pairs of the Laplacian L, the commute-time embedding of the graph’s nodes corresponds to the column vectors of the K × n matrix X:

$X_{K\times n}={\Lambda }_K^{-1/2}{\left(U_{n\times K}\right)}^{\top }=\left[x_1\mathrm{\dots }{x}_j\mathrm{\dots }{x}_n\right].$

(15.53)

From (15.43) and (15.53) one can easily infer lower and upper bounds for the i-th coordinate of x_j:

$-{\lambda }_i^{-1/2}<x_{ji}<{\lambda }_i^{-1/2}.$

(15.54)

The last equation implies that the graph embedding stretches along the eigenvectors with a factor that is inversely proportional to the square root of the eigenvalues. Theorem 15.4.4 below characterizes the smallest non-null K eigenvalue-eigenvector pairs of L as the directions of maximum variance (the principal components) of the commute-time embedding.

Theorem 15.4.4

The largest eigenvalue–eigenvector pairs of the pseudo-inverse of the combinatorial Laplacian matrix are the principal components of the commute-time embedding, i.e., the points X are zero-centered and have a diagonal covariance matrix.

Proof: Indeed, from (15.47) we obtain a zero-mean while from (15.53) we obtain a diagonal covariance matrix:

$\overline{x}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{x}_i=\frac{1}{n}{\Lambda }^{-\frac{1}{2}}\left(\begin{array}{c}{\displaystyle {\sum }_{i=1}^n{u}_{i2}}\\ ⋮\\ {\displaystyle {\sum }_{i=1}^n{u}_{ik+1}}\end{array}\right)=\left(\begin{array}{c}0\\ ⋮\\ 0\end{array}\right)}$

(15.55)

${\Sigma }_X=\frac{1}{n}X{X}^{\top }=\frac{1}{n}{\Lambda }^{-\frac{1}{2}}{U}^{\top }U{\Lambda }^{-\frac{1}{2}}=\frac{1}{n}{\Lambda }^{-1}$

(15.56)

▮

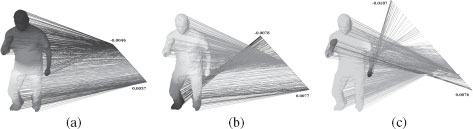
Figure 15.3 shows the projection of graph (in this case 3D shape represented as meshes) vertices on eigenvectors.

15.4.3  Choosing the Dimension of the Embedding

A direct consequence of theorem 15.4.4 is that the embedded graph representation is centered, and the eigenvectors of the combinatorial Laplacian are the directions of maximum variance. The principal eigenvectors correspond to the eigenvectors associated with the K largest eigenvalues of the L^†, i.e., ${\lambda }_2^{-1}\ge {\lambda }_3^{-1}\ge \mathrm{\dots }\ge {\lambda }_K^{-1}$. The variance along vector u_k is ${\lambda }_k^{-1}/n$. Therefore, the total variance can be computed from the trace of the L^† matrix :

$\text{tr}\left({\Sigma }_X\right)=\frac{1}{n}\text{tr}\left(L^{†}\right).$

(15.57)

FIGURE 15.3
This is an illustration of the concept of the PCA of a graph embedding. The graph’s vertices are projected onto the second, third and fourth eigenvectors of the Laplacian matrix. These eigenvectors can be viewed as the principal directions of the shape.

A standard way of choosing the principal components is to use the scree diagram:

$\theta \left(K\right)=\frac{{\displaystyle {\sum }_{k=2}^{K+1}{\lambda }_k^{-1}}}{{\displaystyle {\sum }_{k=2}^n{\lambda }_k^{-1}}}.$

(15.58)

The selection of the first K principal eigenvectors therefore depends on the spectral fall-off of the inverses of the eigenvalues. In spectral graph theory, the dimension K is chosen on the basis of the existence of an eigengap, such that λ_K+2 − λ_K+1 > t with t > 0. In practice, it is extremely difficult to find such an eigengap, in particular in the case of sparse graphs that correspond to a discretized manifold. Instead, we propose to select the dimension of the embedding in the following way. Notice that (15.58) can be written as θ(K) = A/(A+B) with $A={\displaystyle {\sum }_{k=2}^{K+1}{\lambda }_k^{-1}}$ and $B={\displaystyle {\sum }_{k=K+2}^n{\lambda }_k^{-1}}$. Moreover, from the fact that the λ_k’s are arranged in increasing order, we obtain $B\le \left(n-K-1\right){\lambda }_{K+1}^{-1}$. Hence:

${\theta }_{\min }\le \theta \left(K\right)\le 1,$

(15.59)

with

${\theta }_{\min }=\frac{{\displaystyle {\sum }_{k=2}^{K+1}{\lambda }_k^{-1}}}{{\displaystyle {\sum }_{k=2}^K{\lambda }_k^{-1}}+\left(n-K\right){\lambda }_{K+1}^{-1}}.$

(15.60)

This lower bound can be computed from the K smallest non-null eigenvalues of the combinatorial Laplacian matrix. Hence, one can choose K such that the sum of the first K eigenvalues of the L^† matrix is a good approximation of the total variance, e.g., θ_min = 0.95.

15.4.4  Unit Hyper-Sphere Normalization

One disadvantage of the standard embeddings is that when two shapes have large difference in sampling, the embeddings will differ by a significant scale factor. In order to avoid this, we can normalize the embedding such that the vertex coordinates lie on a unit sphere of dimension K, which yields

${\widehat{x}}_i=\frac{x_i}{\Vert x_i\Vert }.$

(15.61)

In more detail, the k-th coordinate of ${\widehat{x}}_i$ writes as

${\widehat{x}}_{ik}=\frac{{\lambda }_k^{-\frac{1}{2}}{u}_{ik}}{{\left({\displaystyle {\sum }_{l=2}^{K+1}{\lambda }_l^{-\frac{1}{2}}{u}_{il}^2}\right)}^{1/2}}.$

(15.62)

15.5  Spectral Shape Matching

In the previous sections we discussed solutions for the exact and inexact graph isomorphism problems, we recalled the main spectral properties of the combinatorial graph Laplacian, and we provided a novel analysis of the commute-time embedding that allows to interpret the latter in terms of the PCA of a graph, and to select the appropriate dimension K ≪ n of the associated embedded metric space. In this section, we address the problem of 3D shape registration, and we illustrate how the material developed above can be exploited in order to build a robust algorithm for spectral shape matching.

Let’s consider two shapes described by two graphs, g_A and g_B, where $\left|{\mathcal{V}}_A\right|=n$ and $\left|{\mathcal{V}}_B\right|=m$. Let L_A and L_B be their corresponding graph Laplacians. Without loss of generality, one can choose the same dimension K ≪ min(n, m) for the two embeddings. This yields the following eigen decompositions:

$L_A=U_{n\times K}{\Lambda }_K{\left(U_{n\times K}\right)}^{\top }$

(15.63)

$L_B={U^{\prime }}_{m\times K}{{\Lambda }^{\prime }}_K{\left({U^{\prime }}_{m\times K}\right)}^{\top }.$

(15.64)

For each one of these graphs, one can build two isomorphic embedded representations, as follows:

•  An unnormalized Laplacian embedding that uses the K rows of U_n×K as the Euclidean coordinates of the vertices of g_A (as well as the K rows of ${U^{\prime }}_{m\times K}$ as the Euclidean coordinates of the vertices of g_B ), and

•  A normalized commute-time embedding given by (15.61), i.e., ${\widehat{X}}_A=\left[{\widehat{x}}_1\mathrm{\dots }{\widehat{x}}_j\mathrm{\dots }{\widehat{x}}_n\right]$ (as well as ${\widehat{X}}_B=\left[{{\widehat{x}}^{\prime }}_1\mathrm{\dots }{{\widehat{x}}^{\prime }}_j\mathrm{\dots }{{\widehat{x}}^{\prime }}_m\right]$). We recall that each column ${\widehat{x}}_j$ (and respectively ${{\widehat{x}}^{\prime }}_j$) is a K-dimensional vector corresponding to a vertex υ_j of g_A (and respectively ${{\upsilon }^{\prime }}_j$ of g_B).

15.5.1  Maximum Subgraph Matching and Point Registration

Let’s apply the graph isomorphism framework of Section 15.3 to the two graphs. They are embedded into two congruent spaces of dimension ${ℝ}^K$. If the smallest K non-null eigenvalues associated with the two embeddings are distinct and can be ordered, i.e.,

${\lambda }_2<\mathrm{\dots }<{\lambda }_k<\mathrm{\dots }<{\lambda }_{K+1}$

(15.65)

${{\lambda }^{\prime }}_2<\mathrm{\dots }<{{\lambda }^{\prime }}_k<\mathrm{\dots }<{{\lambda }^{\prime }}_{K+1}$

(15.66)

then, the Umeyama method could be applied. If one uses the unnormalized Laplacian embeddings just defined, (15.33) becomes

$Q^{\star }=U_{n\times K}{S}_K{\left({U^{\prime }}_{m\times K}\right)}^{\top }$

(15.67)

Notice that here the sign matrix S defined in 15.33 became a K × K matrix denoted by S_K. We now assume that the eigenvalues {λ₂, …, λ_K+1} and $\left\{{{\lambda }^{\prime }}_2,\mathrm{\dots },{{\lambda }^{\prime }}_{K+1}\right\}$ cannot be reliably ordered. This can be modeled by multiplication with a K × K permutation matrix $P_K$:

$Q=U_{n\times K}{S}_K{P}_K{\left({U^{\prime }}_{m\times K}\right)}^{\top }$

(15.68)

Premultiplication of ${\left({U^{\prime }}_{m\times K}\right)}^{\top }$ with P_K permutes its rows such that ${u^{\prime }}_k\to {u^{\prime }}_{\pi \left(k\right)}$. Each entry q_ij of the n × m matrix Q can therefore be written as

$q_{ij}={\displaystyle \sum _{k=2}^{K+1}{s}_k{u}_{ik}{u^{\prime }}_{j\pi \left(k\right)}}$

(15.69)

Since both U_n×K and ${U^{\prime }}_{m\times K}$ are column-orthonormal matrices, the dot-product defined by (15.69) is equivalent to the cosine of the angle between two K-dimensional vectors. This means that each entry of Q is such that −1 ≤ q_ij ≤ +1 and that two vertices υ_i and ${{\upsilon }^{\prime }}_j$ are matched if q_ij is close to 1.

One can also use the normalized commute-time coordinates and define an equivalent expression as above:

$\widehat{Q}={\widehat{X}}^{\top }{S}_K{P}_K{\widehat{X}}^{\prime }$

(15.70)

with:

${\widehat{q}}_{ij}={\displaystyle \sum _{k=2}^{K+1}{s}_k{\widehat{x}}_{ik}{{\widehat{x}}^{\prime }}_{j\pi \left(k\right)}}$

(15.71)

Because both sets of points $\widehat{X}$ and ${\widehat{X}}^{\prime }$ lie on a K-dimensional unit hyper-sphere, we also have $-1\le q_{\widehat{i}j}\le +1$.

It should however be emphasized that the rank of the n × m matrices Q, $\widehat{Q}$ is equal to K. Therefore, these matrices cannot be viewed as relaxed permutation matrices between the two graphs. In fact, they define many-to-many correspondences between the vertices of the first graph and the vertices of the second graph, this being due to the fact that the graphs are embedded on a low-dimensional space. This is one of the main differences between our method proposed in the next section and the Umeyama method, as well as many other subsequent methods, that use all eigenvectors of the graph. As it will be explained below, our formulation leads to a shape-matching method that will alternate between aligning their eigenbases and finding a vertex-to-vertex assignment.

It is possible to extract a one-to-one assignment matrix from Q (or from $\widehat{Q}$) using either dynamic programming or an assignment method technique such as the Hungarian algorithm. Notice that this assignment is conditioned by the choice of a sign matrix S_K and of a permutation matrix P_K, i.e., 2^KK! possibilities, and that not all these choices correspond to a valid subisomorphism between the two graphs. Let’s consider the case of the normalized commute-time embedding; there is an equivalent formulation for the unnormalized Laplacian embedding. The two graphs are described by two sets of points, $\widehat{X}$ and ${\widehat{X}}^{\prime }$, both lying onto the K-dimensional unity hyper-sphere. The K × K matrix S_K P_K transforms one graph embedding onto the other graph embedding. Hence, one can write ${\widehat{x}}_i=S_K{P}_K{{\widehat{x}}^{\prime }}_j$ if vertex υ_i matches υ_j. More generally, let R_K = S_K P_K, and let’s extend the domain of R_K to all possible orthogonal matrices of size K × K, namely $R_K\in {\mathcal{O}}_K$ or the orthogonal group of dimension K. We can now write the following criterion whose minimization over R_K guarantees an optimal solution for registering the vertices of the first graph with the vertices of the second graph:

$\underset{R_K}{\min }{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{\widehat{q}}_{ij}{\Vert {\widehat{x}}_i-R_K{{\widehat{x}}^{\prime }}_j\Vert }^2}}$

(15.72)

One way to solve minimization problems such as (15.72) is to use a point registration algorithm that alternates between (i) estimating the K × K orthogonal transformation R_K, which aligns the K-dimensional coordinates associated with the two embeddings, and (ii) updating the assignment variables ${\widehat{q}}_{ij}$. This can be done using either ICP-like methods (the ${\widehat{q}}_{ij}$’s are binary variables), or EM-like methods (the ${\widehat{q}}_{ij}$’s are posterior probabilities of assignment variables). As we just outlined above, matrix R_K belongs to the orthogonal group ${\mathcal{O}}_K$. Therefore, this framework differs from standard implementations of ICP and EM algorithms that usually estimate a 2-D or 3-D rotation matrix which belong to the special orthogonal group.

It is well established that ICP algorithms are easily trapped in local minima. The EM algorithm recently proposed in [38] is able to converge to a good solution starting with a rough initial guess and is robust to the presence of outliers. Nevertheless, the algorithm proposed in [38] performs well under rigid transformations (rotation and translation), whereas in our case we have to estimate a more general orthogonal transformation that incorporates both rotations and reflections. Therefore, before describing in detail an EM algorithm well suited for solving the problem at hand, we discuss the issue of estimating an initialization for the transformation aligning the K eigenvectors of the first embedding with those of the second embedding, and we propose a practical method for initializing this transformation (namely, matrices S_K and P_K in (15.70)) based on comparing the histograms of these eigenvectors, or eigensignatures.

15.5.2  Aligning Two Embeddings Based on Eigensignatures

Both the unnormalized Laplacian embedding and the normalized commute-time embedding of a graph are represented in a metric space spanned by the eigenvectors of the Laplacian matrix, namely the n-dimensional vectors {u₂, …, u_k,…, u_K+1}, where n is the number of graph vertices. They correspond to eigenfunctions, and each such eigenfunction maps the graph’s vertices onto the real line. More precisely, the k-th eigenfunction maps a vertex υ_i onto u_ik. Propositions 15.4.1 and 15.4.3 revealed interesting statistics of the sets ${\left\{u_{1k},\mathrm{\dots },u_{ik},\mathrm{\dots },u_{nk}\right\}}_{k=2}^{K+1}$. Moreover, Theorem 15.4.4 provided an interpretation of the eigenvectors in terms of principal directions of the embedded shape. One can therefore conclude that the probability distribution of the components of an eigenvector have interesting properties that make them suitable for comparing two shapes, namely −1 < u_ik < +1, ${\overline{u}}_k=1/n{\displaystyle {\sum }_{i=1}^n{u}_{ik}=0}$, and ${\sigma }_k=1/n{\displaystyle {\sum }_{i=1}^n{u}_{ik}^2=1/n}$. This means that one can build a histogram for each eigenvector and that all these histograms share the same bin width w and the same number of bins b [51]:

$w_k=\frac{3.5{\sigma }_k}{n^{1/3}}=\frac{3.5}{n^{4/3}}$

(15.73)

$b_k=\frac{{\sup }_i{u}_{ik}-{\inf }_i{u}_{ik}}{w_k}\approx \frac{n^{4/3}}{2}.$

(15.74)

We claim that these histograms are eigenvector signatures that are invariant under graph isomorphism. Indeed, let’s consider the Laplacian L of a shape and we apply the isomorphic transformation PLP^⊤ to this shape, where P is a permutation matrix. If u is an eigenvector of L, it follows that Pu is an eigenvector of PLP^⊤ and therefore, while the order of the components of u are affected by this transformation, their frequency and hence their probability distributions remain the same. Hence, one may conclude that such a histogram may well be viewed as an eigensignature.

We denote by H{u} the histogram formed with the components of u, and let C(H{u}, H{u′}) be a similarity measure between two histograms. From the eigenvector properties just outlined, it is straightforward to notice that H{u} ≠ H{−u}: These two histograms are mirror symmetric. Hence, the histogram is not invariant to the sign of an eigenvector. Therefore, one can use the eigenvectors’ histograms to estimate both the permutation matrix P_K and the sign matrix S_K in (15.70). The problem of finding one-to-one assignments ${\left\{u_k\leftrightarrow s_k{u^{\prime }}_{\pi \left(k\right)}\right\}}_{k=2}^{K+1}$ between the two sets of eigenvectors associated with the two shapes is therefore equivalent to the problem of finding one-to-one assignments between their histograms.

Let A_K be an assignment matrix between the histograms of the first shape and the histograms of the second shape. Each entry of this matrix is defined by

$a_{kl}=\sup \left[C\left(H\left\{u_k\right\},H\left\{{u^{\prime }}_l\right\}\right);C\left(H\left\{u_k\right\},H\left\{-{u^{\prime }}_l\right\}\right)\right]$

(15.75)

Similarly, we define a matrix B_K that accounts for the sign assignments:

$b_{kl}=\{\begin{array}{l}+1\text{if }C\left(H\left\{u_k\right\},H\left\{{u^{\prime }}_l\right\}\right)\ge C\left(H\left\{u_k\right\},H\left\{-{u^{\prime }}_l\right\}\right)\hfill \\ -1\text{if}C\left(H\left\{u_k\right\},H\left\{{u^{\prime }}_l\right\}\right)<C\left(H\left\{u_k\right\},H\left\{-{u^{\prime }}_l\right\}\right)\hfill \end{array}$

(15.76)

Extracting a permutation matrix P_K from A_K is an instance of the bipartite maximum matching problem, and the Hungarian algorithm is known to provide an optimal solution to this assignment problem [47]. Moreover, one can use the estimated P_K to extract a sign matrix S_K from B_K. Algorithm 3 estimates an alignment between two embeddings.

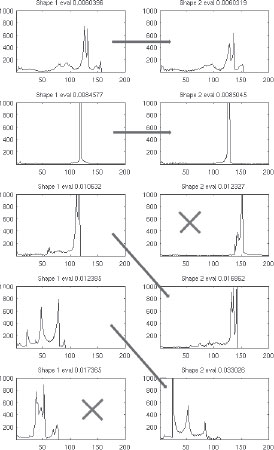
Figure 15.4 illustrates the utility of the histogram of eigenvectors as eigensignatures for solving the problem of sign flip and change in eigenvector ordering by computing histogram matching. It is interesting to observe that a threshold on the histogram matching score (15.75) allows us to discard the eigenvectors with low similarity cost. Hence, starting with large K obtained using (15.60), we can limit the number of eigenvectors to just a few, which will be suitable for EM-based point registration algorithm proposed in the next section.

15.5.3  An EM Algorithm for Shape Matching

As explained in section 15.5.1, the maximum subgraph matching problem reduces to a point registration problem in K-dimensional metric space spanned by the eigenvectors of graph Laplacian where two shapes are represented as point clouds. The initial alignment of Laplacian embeddings can be obtained by matching the histogram of eigenvectors as described in the previous section. In this section, we propose an EM algorithm for 3D shape matching that computes a probabilistic vertex-to-vertex assignment between two shapes. The proposed method alternates between the step to estimate an orthogonal transformation matrix associated with the alignment of the two shape embeddings and the step to compute a point-to-point probabilistic assignment variable.

FIGURE 15.4
An illustration of applicability of eigenvector histogram as eigensignature to detect sign flip and eigenvector ordering change. The blue line shows matched eigenvector pairs, and the red cross depicts discarded eigenvectors.

The method is based on a parametric probabilistic model, namely maximum likelihood with missing data. Let us consider the Laplacian embedding of two shapes, i.e., (15.53): $\widehat{X}={\left\{{\widehat{x}}_i\right\}}_{i=1}^n,{\widehat{X}}^{\prime }={\left\{{{\widehat{x}}^{\prime }}_j\right\}}_{j=1}^m$, with $\widehat{X},{\widehat{X}}^{\prime }\subset {ℝ}^K$. Without loss of generality, we assume that the points in the first set, $\widehat{X}$ are cluster centers of a Gaussian mixture model (GMM) with n clusters and an additional uniform component that accounts for outliers and unmatched data. The matching $\widehat{X}\leftrightarrow {\widehat{X}}^{\prime }$ will consist in fitting the Gaussian mixture to the set ${\widehat{X}}^{\prime }$.

Let this Gaussian mixture undergo a K × K transformation R (for simplicity, we omit the index K) with R^⊤R = I_K, det(R) = ±1, more precisely $R\in {\mathcal{O}}_K$, the group of orthogonal matrices acting on ${ℝ}^K$. Hence, each cluster in the mixture is parametrized by a prior p_i, a cluster mean ${\mu }_i=R{\widehat{x}}_i$, and a covariance matrix Σ_i. It will be assumed that all the clusters in the mixture have the same priors, ${\left\{p_i={\pi }_{\text{in}}\right\}}_{i=1}^n$, and the same isotropic covariance matrix, ${\left\{{\Sigma }_i=\sigma I_K\right\}}_{i=1}^n$. This parametrization leads to the following observed-data log-likelihood (with π_out = 1 − nπ_in and $\mathcal{U}$ is the uniform distribution):

$\log P\left({\widehat{X}}^{\prime }\right)={\displaystyle \sum _{j=1}^m\log \left({\displaystyle \sum _{i=1}^n{\pi }_{\text{in}}\mathcal{N}\left({{\widehat{x}}^{\prime }}_j|{\mu }_i,\sigma \right)+{\pi }_{\text{out}}\mathcal{U}}\right)}$

(15.77)

It is well known that the direct maximization of (15.77) is not tractable, and it is more practical to maximize the expected complete-data log-likelihood using the EM algorithm, where “complete-data” refers to both the observed data (the points ${\widehat{X}}^{\prime }$) and the missing data (the data-to-cluster assignments). In our case, the above expectation writes (see [38] for details)

$ℰ\left(R,\sigma \right)=-\frac{1}{2}{\displaystyle \sum _{j=1}^m{\displaystyle \sum _{i=1}^n{\alpha }_{ji}\left({\Vert {{\widehat{x}}^{\prime }}_j-R{\widehat{x}}_i\Vert }^2+k\log \sigma \right)},}$

(15.78)

where α_ji denotes the posterior probability of an assignment ${{\widehat{x}}^{\prime }}_j\leftrightarrow {\widehat{x}}_i$:

${\alpha }_{ji}=\frac{\exp \left(-{\Vert {{\widehat{x}}^{\prime }}_j-R{\widehat{x}}_i\Vert }^2/2\sigma \right)}{{\displaystyle {\sum }_{q=1}^n\exp \left(-{\Vert {{\widehat{x}}^{\prime }}_j-R{\widehat{x}}_q\Vert }^2/2\sigma \right)+\cancel{0}{\sigma }^{k/2}}},$

(15.79)

where $\cancel{0}$ is a constant term associated with the uniform distribution $\mathcal{U}$. Notice that one easily obtains the posterior probability of a data point to remain unmatched, ${\alpha }_{jn+1}=1-{\displaystyle {\sum }_{i=1}^n{\sigma }_{ij}}$. This leads to the shape-matching procedure outlined in Algorithm 4.

15.6  Experiments and Results

We have performed several 3D shape registration experiments to evaluate the proposed method. In the first experiment, 3D shape registration is performed on 138 high-resolution (10K-50K vertices) triangular meshes from the publicly available TOSCA dataset [33]. The dataset includes 3 shape classes (human, dog, horse) with simulated transformations. Transformations are split into 9 classes (isometry, topology, small and big holes, global and local scaling, noise, shot noise, sampling). Each transformation class appears in five different strength levels. An estimate of average geodesic distance to ground truth correspondence was computed for performance evaluation (see [33] for details).

We evaluate our method in two settings. In the first setting SM1, we use the commute-time embedding (15.53) while in the second setting SM2, we use the unit hyper-sphere normalized embedding (15.61).

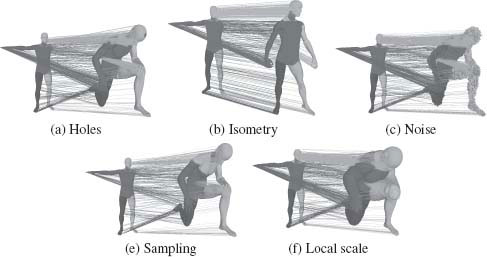
Table 15.2 shows the error estimates for dense shape matching using the proposed spectral matching method. In the case of some transforms, the proposed method yields zero error because the two meshes had identical triangulations. Figure 15.5 shows some matching results. The colors emphasize the correct matching of body parts, while we show only 5% of matches for better visualization. In Figure 15.5(e), the two shapes have large difference in the sampling rate. In this case, the matching near the shoulders is not fully correct since we used the commute-time embedding.

Table 15.3 summarizes the comparison of proposed spectral matching method (SM1 and SM2) with generalized multidimensional scaling (GMDS) based matching algorithm introduced in [19] and the Laplace–Beltrami matching algorithm proposed in [12] with two settings LB1 (uses graph Laplacian) and LB2 (uses cotangent weights). GMDS computes the correspondence between two shapes by trying to embed one shape into another with minimum distortion. LB1 and LB2 algorithms combines the surface descriptors based on the eigendecomposition of the Laplace–Beltrami operator and the geodesic distances measured on the shapes when calculating the correspondence quality. The above results in a quadratic optimization problem formulation for correspondence detection, and its minimizer is the best possible correspondence. The proposed method clearly outperform the other two methods with minimum average error estimate computed over all the transformations in the dataset.

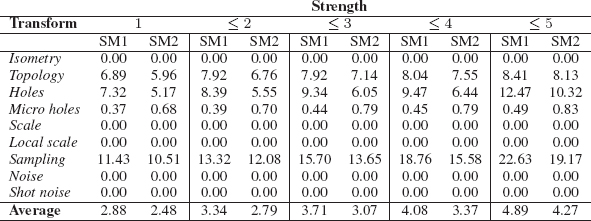
TABLE 15.2
3D shape registration error estimates (average geodesic distance to ground truth correspondences) using proposed spectral matching method with commute-time embedding (SM1) and unit hyper-sphere normalized embedding (SM2).

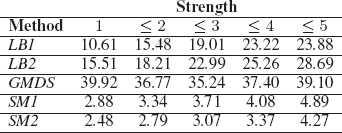
TABLE 15.3
Average shape registration error estimates over all transforms (average geodesic distance to ground truth correspondences) computed using proposed methods (SM1 and SM2), GMDS [19] and LB1, LB2 [12].

		Strength
Transform	1	≤ 3	≤ 5
Isometry	SM1,SM2	SM1,SM2	SM1,SM2
Topology	SM2	SM2	SM2
Holes	SM2	SM2	SM2
Micro holes	SM1	SM1	SM1
Scale	SM1,SM2	SM1,SM2	SM1,SM2
Local scale	SM1,SM2	SM1,SM2	SM1,SM2
Sampling	LB1	SM2	LB2
Noise	SM1,SM2	SM1,SM2	SM1,SM2
Shot noise	SM1,SM2	SM1,SM2	SM1,SM2
Average	SM1,SM2	SM1,SM2	SM1,SM2

TABLE 15.4
3D shape registration performance comparison: The proposed methods (SM1 and SM2) performed best by providing minimum average shape registration error over all the transformation classes with different strength as compare to GMDS [19] and LB1, LB2 [12] methods.

FIGURE 15.5
3D shape registration in the presence of different transforms.

In Table 15.4, we show a detailed comparison of the proposed method with other methods. For a detailed quantitative comparison refer to [33]. The proposed method inherently uses diffusion geometry as opposed to geodesic metric used by other two methods and hence outperform them.

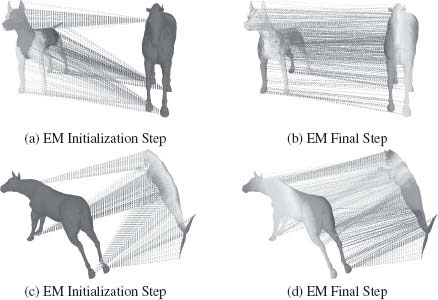
In the second experiment, we perform shape registration on two different shapes with similar topology. In Figure 15.6, results of shape registration on different shapes is presented. Figure 15.6(a),(c) shows the initialization step of EM algorithm while Figure 15.6(b),(d) shows the dense matching obtained after EM convergence.

FIGURE 15.6
3D shape registration performed on different shapes with similar topology.

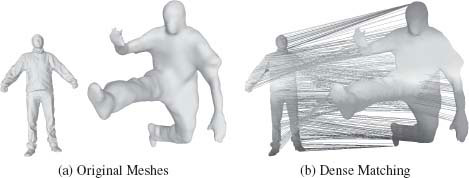
Finally, we show shape-matching results on two different human meshes captured with a multi-camera system at MIT [5] and University of Surrey [2] in Figure 15.7

15.7  Discussion

This chapter describes a 3D shape registration approach that computes dense correspondences between two articulated objects. We address the problem using spectral matching and unsupervised point registration method. We formally introduce graph isomorphism using the Laplacian matrix, and we provide an analysis of the matching problem when the number of nodes in the graph is very large, that is, of the order of O(10⁴). We show that there is a simple equivalence between graph isomorphism and point registration under the group of orthogonal transformations, when the dimension of the embedding space is much smaller than the cardinality of the point-sets.

FIGURE 15.7
3D shape registration performed on two real meshes captured from different sequence.

The eigenvalues of a large sparse Laplacian cannot be reliably ordered. We propose an elegant alternative to eigenvalue ordering, using eigenvector histograms and alignment based on comparing these histograms. The point registration that results from eigenvector alignment yields an excellent initialization for the EM algorithm, subsequently used only to refine the registration.

However, the method is susceptible to large topology changes that might occur in the multi-camera shape acquisition setup due to self-occlusion (originated from complex kinematics poses) and shadow effects. This is because Laplacian embedding is a global representation and any major topology change will lead to large changes in embeddings causing failure of this method. Recently, a new shape registration method proposed in [36] provides robustness to the large topological changes using the heat kernel framework.

15.8  Appendix: Permutation and Doubly-stochastic Matrices

A matrix P is called a permutation matrix if exactly one entry in each row and column is equal to 1, and all other entries are 0. Left multiplication of a matrix A by a permutation matrix P permutes the rows of A, while right multiplication permutes the columns of A.

Permutation matrices have the following properties: det(P) = ±1, P^⊤ = P⁻¹, the identity is a permutation matrix, and the product of two permutation matrices is a permutation matrix. Hence, the set of permutation matrices $P\in {\mathcal{P}}_n$ constitute a subgroup of the subgroup of orthogonal matrices, denoted by ${\mathcal{O}}_n$, and ${\mathcal{P}}_n$ has finite cardinality n!.

A non-negative matrix A is a matrix such that all its entries are non-negative. A non-negative matrix with the property that all its row sums are +1 is said to be a (row) stochastic matrix. A column stochastic matrix is the transpose of a row stochastic matrix. A stochastic matrix A with the property that A^⊤ is also stochastic is said to be doubly stochastic: all row and column sums are +1 and a_ij ≥ 0. The set of stochastic matrices is a compact convex set with the simple and important property that A is stochastic if and only if $A1=1$, where $1$ is the vector with all components equal to +1.

Permutation matrices are doubly stochastic matrices. If we denote by ${\mathcal{D}}_n$ the set of doubly stochastic matrices, it can be proved that ${\mathcal{P}}_n={\mathcal{O}}_n\cap {\mathcal{D}}_n$ [52]. The permutation matrices are the fundamental and prototypical doubly stochastic matrices, for Birkhoff’s theorem states that any doubly stochastic matrix is a linear convex combination of finitely many permutation matrices [46]

Theorem 15.8.1

(Birkhoff) A matrix A is a doubly stochastic matrix if and only if for some N < ∞ there are permutation matrices P₁,…, P_N and positive scalars s₁,…, s_N such that s₁ + … + s_N = 1 and A = s₁P₁ + … + s_NP_N.

A complete proof of this theorem is to be found in [46][pages 526–528]. The proof relies on the fact that ${\mathcal{D}}_n$ is a compact convex set, and every point in such a set is a convex combination of the extreme points of the set. First, it is proved that every permutation matrix is an extreme point of ${\mathcal{D}}_n$ and, second, it is shown that a given matrix is an extreme point of ${\mathcal{D}}_n$ if an only if it is a permutation matrix.

15.9  Appendix: The Frobenius Norm

The Frobenius (or Euclidean) norm of a matrix A_n×n is an entry-wise norm that treats the matrix as a vector of size 1 × nn. The standard norm properties hold: ${\Vert A\Vert }_F>0\iff A\ne 0,{\Vert A\Vert }_F=0\iff A=0,{\Vert cA\Vert }_F=c{\Vert A\Vert }_F$, and ${\Vert A+B\Vert }_F\le {\Vert A\Vert }_F+{\Vert B\Vert }_F$. Additionally, the Frobenius norm is sub-multiplicative:

${\Vert AB\Vert }_F\le {\Vert A\Vert }_F{\Vert B\Vert }_F$

(15.80)

as well as unitarily invariant. This means that for any two orthogonal matrices U and V:

${\Vert UAV\Vert }_F={\Vert A\Vert }_F.$

(15.81)

It immediately follows the following equalities:

${\Vert UA{V}^{\top }\Vert }_F={\Vert UA\Vert }_F={\Vert AU\Vert }_F={\Vert A\Vert }_F.$

(15.82)

15.10  Appendix: Spectral Properties of the Normalized Laplacian

The Normalized Laplacian

Let ${\tilde{u}}_k$ and γ_k denote the eigenvectors and eigenvalues of $\tilde{L}$; The spectral decomposition is $\tilde{L}=\tilde{U}\Gamma {\tilde{U}}^{\top }$ with $\tilde{U}{\tilde{U}}^{\top }=I$. The smallest eigenvalue and associated eigenvector are γ₁ = 0 and ${\tilde{u}}_1=D^{1/2}1$.

We obtain the following equivalent relations:

${\displaystyle {\sum }_{i=1}^n{d}_i^{1/2}{\tilde{u}}_{ik}=0,2\le k\le n}$

(15.83)

$d_i^{1/2}\left|{\tilde{u}}_{ik}\right|<1,1\le i\le n,2\le k\le n.$

(15.84)

Using (15.5) we obtain a useful expression for the combinatorial Laplacian in terms of the spectral decomposition of the normalized Laplacian. Notice, however, that the expression below is NOT a spectral decomposition of the combinatorial Laplacian:

$L=\left(D^{1/2}\tilde{U}{\Gamma }^{1/2}\right){\left(D^{1/2}\tilde{U}{\Gamma }^{1/2}\right)}^{\top }.$

(15.85)

For a connected graph γ₁ has multiplicity 1: 0 = γ₁ < γ₂ < … ≤ γ_n. As in the case of the combinatorial Laplacian, there is an upper bound on the eigenvalues (see [41] for a proof):

Proposition 15.10.1

For all k ≤ n, we have μ_k ≤ 2.

We obtain the following spectral decomposition for the normalized Laplacian:

$\tilde{L}={\displaystyle \sum _{k=2}^n{\gamma }_k{\tilde{u}}_k{\tilde{u}}_k^{\top }.}$

(15.86)

The spread of the graph along the k-th normalized Laplacian eigenvector is given by ∀(k, i), 2 ≤ k ≤ n, 1 ≤ i < n:

${\overline{\tilde{u}}}_k=\frac{1}{k}{\displaystyle \sum _{i=1}^n{\tilde{u}}_{ik}}$

(15.87)

${\sigma }_{u_k}=\frac{1}{n}-{\overline{\tilde{u}}}_k^2.$

(15.88)

Therefore, the projection of the graph onto an eigenvector ${\tilde{u}}_k$ is not centered. By combining (15.5) and (15.86), we obtain an alternative representation of the combinatorial Laplacian in terms of the the spectrum of the normalized Laplacian, namely:

$L={\displaystyle \sum _{k=2}^n{\gamma }_k\left(D^{1/2}{\tilde{u}}_k\right){\left(D^{1/2}{\tilde{u}}_k\right)}^{\top }.}$

(15.89)

Hence, an alternative is to project the graph onto the vectors $t_k=D^{1/2}{\tilde{u}}_k$. From ${\tilde{u}}_{k\ge 2}^{\top }{\tilde{u}}_1=0$ we get that $t_{k\ge 2}^{\top }1=0$. Therefore, the spread of the graph’s projection onto t_k has the following mean and variance, ∀(k, i), 2 ≤ k ≤ n, 1 ≤ i ≤ n:

${\overline{t}}_k={\displaystyle {\sum }_{i=1}^n{d}_i^{1/2}{\tilde{u}}_{ik}=0}$

(15.90)

${\sigma }_{t_k}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{d}_i{\tilde{u}}_{ik}^2.}$

(15.91)

The Random-Walk Laplacian.

This operator is not symmetric, however, its spectral properties can be easily derived from those of the normalized Laplacian using (15.7). Notice that this can be used to transform a nonsymmetric Laplacian into a symmetric one, as proposed in [53] and in [54].

Bibliography

[1]  J.-S. Franco and E. Boyer, “Efficient Polyhedral Modeling from Silhouettes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 3, pp. 414—427, 2009.

[2]  J. Starck and A. Hilton, “Surface capture for performance based animation,” IEEE Computer Graphics and Applications, vol. 27, no. 3, pp. 21–31, 2007.

[3]  G. Slabaugh, B. Culbertson, T. Malzbender, and R. Schafer, “A survey of methods for volumetric scene reconstruction from photographs,” in International Workshop on Volume Graphics, 2001, pp. 81–100.

[4]  S. M. Seitz, B. Curless, J. Diebel, D. Scharstein, and R. Szeliski, “A comparison and evaluation of multi-view stereo reconstruction algorithms,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2006, pp. 519–528.

[5]  D. Vlasic, I. Baran, W. Matusik, and J. Popovic, “Articulated mesh animation from multi-view silhouettes,” ACM Transactions on Graphics (Proc. SIGGRAPH), vol. 27, no. 3, pp. 97:1–97:9, 2008.

[6]  A. Zaharescu, E. Boyer, and R. P. Horaud, “Topology-adaptive mesh deformation for surface evolution, morphing, and multi-view reconstruction,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 4, pp. 823 – 837, April 2011.

[7]  Y. Chen and G. Medioni, “Object modelling by registration of multiple range images,” Image Vision Computing, vol. 10, pp. 145–155, April 1992.

[8]  P. J. Besl and N. D. McKay, “A method for registration of 3-d shapes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 14, pp. 239–256, February 1992.

[9]  S. Rusinkiewicz and M. Levoy, “Efficient variants of the ICP algorithm,” in International Conference on 3D Digital Imaging and Modeling, 2001, pp. 145–152.

[10]  S. Umeyama, “An eigendecomposition approach to weighted graph matching problems,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 10, no. 5, pp. 695–703, May 1988.

[11]  J. H. Wilkinson, “Elementary proof of the Wielandt-Hoffman theorem and of its generalization,” Stanford University, Tech. Rep. CS150, January 1970.

[12]  A. Bronstein, M. Bronstein, and R. Kimmel, “Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching,” Proceedings of National Academy of Sciences, vol. 103, pp. 1168–1172, 2006.

[13]  S. Wang, Y. Wang, M. Jin, X. Gu, D. Samaras, and P. Huang, “Conformal geometry and its application on 3d shape matching,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 29, no. 7, pp. 1209–1220, 2007.

[14]  V. Jain, H. Zhang, and O. van Kaick, “Non-rigid spectral correspondence of triangle meshes,” International Journal of Shape Modeling, vol. 13, pp. 101–124, 2007.

[15]  W. Zeng, Y. Zeng, Y. Wang, X. Yin, X. Gu, and D. Samras, “3D non-rigid surface matching and registration based on holomorphic differentials,” in European Conference on Computer Vision, 2008, pp. 1–14.

[16]  D. Mateus, R. Horaud, D. Knossow, F. Cuzzolin, and E. Boyer, “Articulated shape matching using Laplacian eigenfunctions and unsupervised point registration,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2008, pp. 1–8.

[17]  M. R. Ruggeri, G. Patané, M. Spagnuolo, and D. Saupe, “Spectral-driven isometry-invariant matching of 3d shapes,” International Journal of Computer Vision, vol. 89, pp. 248–265, 2010.

[18]  Y. Lipman and T. Funkhouser, “Mobius voting for surface correspondence,” ACM Transactions on Graphics (Proc. SIGGRAPH), vol. 28, no. 3, pp. 72:1–72:12, 2009.

[19]  A. Dubrovina and R. Kimmel, “Matching shapes by eigendecomposition of the Laplace-Beltrami operator,” in International Symposium on 3D Data Processing, Visualization and Transmission, 2010.

[20]  G. Scott and C. L. Higgins, “An Algorithm for Associating the Features of Two Images,” Biological Sciences, vol. 244, no. 1309, pp. 21–26, 1991.

[21]  L. S. Shapiro and J. M. Brady, “Feature-based correspondence: an eigenvector approach,” Image Vision Computing, vol. 10, pp. 283–288, June 1992.

[22]  B. Luo and E. R. Hancock, “Structural graph matching using the em algorithm and singular value decomposition,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 23, pp. 1120–1136, October 2001.

[23]  H. F. Wang and E. R. Hancock, “Correspondence matching using kernel principal components analysis and label consistency constraints,” Pattern Recognition, vol. 39, pp. 1012–1025, June 2006.

[24]  H. Qiu and E. R. Hancock, “Graph simplification and matching using commute times,” Pattern Recognition, vol. 40, pp. 2874–2889, October 2007.

[25]  M. Leordeanu and M. Hebert, “A spectral technique for correspondence problems using pairwise constraints,” in International Conference on Computer Vision, 2005, pp. 1482–1489.

[26]  O. Duchenne, F. Bach, I. Kweon, and J. Ponce, “A tensor based algorithm for high order graph matching,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2009, pp. 1980–1987.

[27]  L. Torresani, V. Kolmogorov, and C. Rother, “Feature correspondence via graph matching : Models and global optimazation,” in European Conference on Computer Vision, 2008, pp. 596–609.

[28]  R. Zass and A. Shashua, “Probabilistic graph and hypergraph matching,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2008, pp. 1–8.

[29]  J. Maciel and J. P. Costeira, “A global solution to sparse correspondence problems,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 25, pp. 187–199, 2003.

[30]  Q. Huang, B. Adams, M. Wicke, and L. J. Guibas, “Non-rigid registration under isometric deformations,” Computer Graphics Forum, vol. 27, no. 5, pp. 1449–1457, 2008.

[31]  Y. Zeng, C. Wang, Y. Wang, X. Gu, D. Samras, and N. Paragios, “Dense non-rigid surface registration using high order graph matching,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2010, pp. 382–389.

[32]  Y. Sahillioglu and Y. Yemez, “3d shape correspondence by isometry-driven greedy optimization,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2010, pp. 453–458.

[33]  A. M. Bronstein, M. M. Bronstein, U. Castellani, A. Dubrovina, L. J. Guibas, R. P. Horaud, R. Kimmel, D. Knossow, E. v. Lavante, M. D., M. Ovsjanikov, and A. Sharma, “Shrec 2010: robust correspondence benchmark,” in Eurographics Workshop on 3D Object Retrieval, 2010.

[34]  M. Ovsjanikov, Q. Merigot, F. Memoli, and L. Guibas, “One point isometric matching with the heat kernel,” Computer Graphics Forum (Proc. SGP), vol. 29, no. 5, pp. 1555–1564, 2010.

[35]  A. Sharma and R. Horaud, “Shape matching based on diffusion embedding and on mutual isometric consistency,” in NORDIA workshop IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2010.

[36]  A. Sharma, R. Horaud, J. Cech, and E. Boyer, “Topologically-robust 3D shape matching based on diffusion geometry and seed growing,” in IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2011.

[37]  D. Knossow, A. Sharma, D. Mateus, and R. Horaud, “Inexact matching of large and sparse graphs using laplacian eigenvectors,” in Graph-Based Representations in Pattern Recognition, 2009, pp. 144–153.

[38]  R. P. Horaud, F. Forbes, M. Yguel, G. Dewaele, and J. Zhang, “Rigid and articulated point registration with expectation conditional maximization,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 3, pp. 587–602, 2011.

[39]  M. Belkin and P. Niyogi, “Laplacian eigenmaps for dimensionality reduction and data representation,” Neural computation, vol. 15, no. 6, pp. 1373–1396, 2003.

[40]  U. von Luxburg, “A tutorial on spectral clustering,” Statistics and Computing, vol. 17, no. 4, pp. 395–416, 2007.

[41]  F. R. K. Chung, Spectral Graph Theory. American Mathematical Society, 1997.

[42]  L. Grady and J. R. Polimeni, Discrete Calculus: Applied Analysis on Graphs for Computational Science. Springer, 2010.

[43]  C. Godsil and G. Royle, Algebraic Graph Theory. Springer, 2001.

[44]  A. J. Hoffman and H. W. Wielandt, “The variation of the spectrum of a normal matrix,” Duke Mathematical Journal, vol. 20, no. 1, pp. 37–39, 1953.

[45]  J. H. Wilkinson, The Algebraic Eigenvalue Problem. Oxford: Clarendon Press, 1965.

[46]  R. A. Horn and C. A. Johnson, Matrix Analysis. Cambridge: Cambridge University Press, 1994.

[47]  R. Burkard, Assignment Problems. Philadelphia: SIAM, Society for Industrial and Applied Mathematics, 2009.

[48]  J. Ham, D. D. Lee, S. Mika, and B. Schölkopf, “A kernel view of the dimensionality reduction of manifolds,” in International Conference on Machine Learning, 2004, pp. 47–54.

[49]  H. Qiu and E. R. Hancock, “Clustering and embedding using commute times,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 29, no. 11, pp. 1873–1890, 2007.

[50]  C. M. Grinstead and L. J. Snell, Introduction to Probability. American Mathematical Society, 1998.

[51]  D. W. Scott, “On optimal and data-based histograms,” Biometrika, vol. 66, no. 3, pp. 605–610, 1979.

[52]  M. M. Zavlanos and G. J. Pappas, “A dynamical systems approach to weighted graph matching,” Automatica, vol. 44, pp. 2817–2824, 2008.

[53]  J. Sun, M. Ovsjanikov, and L. Guibas, “A concise and provably informative multi-scale signature based on heat diffusion,” in SGP, 2009.

[54]  C. Luo, I. Safa, and Y. Wang, “Approximating gradients for meshes and point clouds via diffusion metric,” Computer Graphics Forum (Proc. SGP), vol. 28, pp. 1497–1508, 2009.