Chapter Eight

Trial-and-Error Searching, Maple Programming; Dipstick Calibration

8.1 PROBLEM: VOLUME OF LIQUID IN SPHERICAL TANKS

A spherical tank of radius R=3 meters is to be used to hold gas. You are given a stick to dip into the tank, and you want to calibrate the scale on it such that it reads the volume of fluid in the tank (see Figure 8.1). Your problem is to determine the height of the fluid for a given volume. Hint: use an indirect approach by calculating the volume for a series of heights until some height gives you the volume you are looking for.

8.2 MATH: VOLUME INTEGRATION

It seems straightforward to calculate V (H), the volume of the liquid in the tank as a function of height H. Once we have that, the hard problem is to invert the solution, that is determine H(V ). Consider Figure 8.1. The volume of a disk of differential thickness dh and radius r is

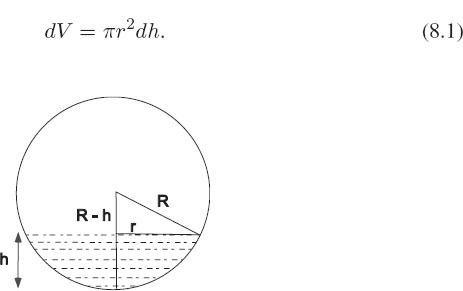
Figure 8.1 A spherical tank of radius R filled with a liquid to height H above its bottom.

Here the height varies over the range 0≤h≤H, and the radius r is related to the variable height h via Pythagoras’s theorem:

Indeed, if h = 2R, then r = 0, as it should. We evaluate the volume by adding up the volumes of all the differential disks:

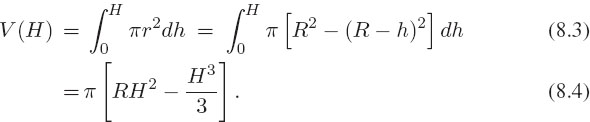
Equation (8.4) gives the volume of fluid as a function of its height. As a check we see that for an empty tank V (0) = 0, and that for a full tank V (2R) = ⁴/₃πR³.

Our problem requires us to deduce the height for a known volume. To do that we rewrite (8.4) as the cubic equation

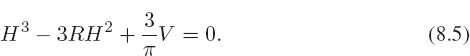
For R=3 and a sample volume V = ⁴/₃π, the equation to solve is

Here (8.6) is in the standard f(h) = 0 form. We know from the geometry of the problem that the solution we want must lie in the range

Because f(H = 0) = 4 and f(H = 2R = 6) = –105, we know that our function must pass through zero in this range.

Regardless of the existence of closed-form expressions for the solutions of cubic equations, we shall solve it numerically (a procedure you would have to follow anyway if there were higher powers than the third). In spite of the fact that Maple’s fsolve command is applicable, we wish to understand what goes on inside that command and to get some programming experience.

8.3 ALGORITHM: BISECTION SEARCHES

A traditional computational technique is “trial and error,” in which a program starts with a trial solution, determines how large the error is, and then makes a new guess based on the error. The procedure keeps repeating until the error becomes acceptably small. These trial-and-error programs are interesting to write because they must be intelligent, and interesting to run because you are not sure how long it will take to find a solution, or whether a solution will be found at all.

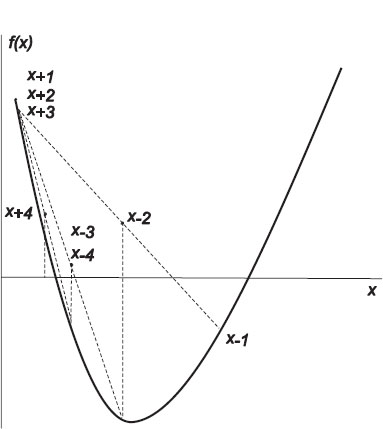
Figure 8.2 A graphical representation of the steps involved in solving for a zero of f(x) using the bisection algorithm. In each step the algorithm takes the midpoint of the interval as its new guess for x, thereby reducing the interval’s size by one half. The first interval is (x₁, x-₁), the second (x₂, x-₂), etc.

The most elementary trial-and-error technique is the bisection algorithm. Its basis, shown in Figure 8.2, starts with two values, x- and x₊, between which we know a zero occurs. We assume that f(x) is negative at x- and positive at x₊:

This approach does not limit us in any way, since it just means that if the function changes from positive to negative as x increases, then x- will be greater than x₊. The algorithm bisects the interval to obtain the midpoint

and then checks if there is a sign change in the right half of the interval. If there is, then it limits the search to the right half-interval only; if not, then it limits the search to the left half-interval. In either case the regions to be searched decrease by one half each time.

In Figure 8.2 the first interval extends from x- =x₊₁ to x₊ =x-₁. We bisect that interval at x, and since f(x) < 0 at the midpoint, we set x- ≡ x-₂ = x and label it x-₂ to indicate the second step. We then use x₊₂ ≡x₊₁ and x-₂ as the next interval and continue the process. We see in the figure that only x-changes for the first three steps, but that for the fourth step, x₊ finally changes. After that, the changes get too small for us to show.

Table 8.1 Maple’s relational operators.

< less than	<= less than or equal to	> greater than
>= greater than or equal to	= equals	<> not equal to

8.4 PROGRAMMING IN MAPLE

We have already done some Maple programming when we defined arrow functions to represent expressions. This is fine as long as the function definition fits on one line. However, sometimes we need to include a number of steps in a calculation, and we cannot do that with an arrow function. In these latter cases we need to write a multiline program, often with logic deciding which path to follow through the program. In the sections to follow we explore some of the features of Maple that are useful for programming. Notwithstanding the usefulness of programming with Maple for honing your programming skills, we recommend that you also experience the more powerful programming possible with compiled languages like Java and Fortran. We do that in Part 2 of this book. Even if you do not intend to be programming in Maple, the programming here will serve well as an introduction to general programming.

8.4.1 Logic

The first step in having the computer make intelligent decisions is having it be able to tell if a statement is true or false. This is accomplished with Boolean variables, that is, variables that are either true or false. Objects that have true and false values may also be constructed from expressions. To construct a Boolean expression, you use relational and logical operators to combine ordinary variables. The relational operators in Maple are as shown in Table 8.1. To prove the point, 1<2 is true, as is 1 <= 1, while 2 <> 2 is false, as is 2 > 3. To determine what Maple believes to be true, we evaluate an expression as Boolean using the evalb command:

More involved logical expressions are created by combining simple Boolean expressions by use of the three logical, or conditional, operators, and, or, and not. The basic logic behind logical operators is that compound statements constructed

Table 8.2 A truth table showing how Boolean variables combine.

True	False	True	False
true and true	true and false	true or true	false and false
true or false	false or false	not false	not true

from simpler statements obey the truth table, Table 8.2. As an example, here we construct and test some more complex logical expressions:

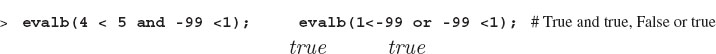
8.4.2 Flow Control

The basic logic command used to control program flow is the if statement:

if a statement is true, then do something, else do something different.

Maple uses a particular notation for this:

Here <logical expression> is a Boolean expression, <statements> is any sequence of Maple statements that you care to include, and if, end if, else, and elif are Maple key words (the last is shorthand for else if). Take note that every if must have a matching end if, and that the variables in the logical expressions must have numerical values to avoid complaints from Maple. As we shall see below, it is permissible to use just part of the full construct, if that is all you need. As a case in point, to use just if and then.

We start with a simple test that may be useful for programming a thermostat. If the temperature T is negative, then we need more Heat:

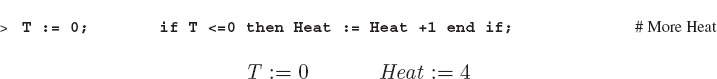
We see that Maple discerns whether T is positive or negative and acts appropriately. Maple will then increase the Heat for negative T but not change the Heat for positive T. Try out these same conditions using an if command that tests if T is positive or not negative:

Up until this point, we have a thermostat that is able to turn up the heat when it is cold but not turn it down when it gets hot. We fix that via two sequential tests:

We accomplish the same goal in just one line by invoking the else if construct, that Maple calls elif:

In conclusion, it is possible to construct all logical conditions that may exist by combining the simple Boolean operators and expressions. In particular, it is permissible to keep concatenating if statements to be as specific as you like.

8.4.3 for Loop

An essential component of scientific computing involves having the computer repeat a set of commands until some predefined condition is met. This may be until a desired level of precision is achieved, until a matrix or a vector has been spanned, or this may be to step through space or time in discrete steps. We discuss the way to do this in Java in Chapters 12 and 14, where we loop over time steps for projectiles and over space steps for integration. Here we discuss how to do this in Maple.

We have already seen Maple looping in Chapter 5 where we summed up the height of blocks to obtain the height of a tower:

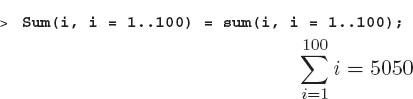
In this case, Maple has an internal program that loops over the sum. We do the same thing ourselves using Maple’s for construct:

for <variable> from <expression> by <expression> to <expression>,

where not all parts must be used at any one time, although do and end do are always required. So we write our own sum:

Here all the lines between the do and end do statements get repeated for as long as the condition specified by the for .. from .. to .. construct holds true. In the present case, the for construct increases i from 1 to 10, and the loop increases mySum by i each time the loop is repeated. For more involved computations there may be many lines between the beginning and end of the do loop. As is often the case with loops, some variables must be initialized before the loop begins, as we do here with mySum: = 0;. Take note, you will avoid the 100 lines of intermediate output by replacing the “;” on the end do line with a “:”.

For some applications you may wish to change the loop index (counter) by a number other than 1. (Normally you may leave out the from and by parts of the construct and let them have their default values of 1.) For loops that do not increment by 1, you use the by construct and pick what change you would like; for example, here we sum all the even number from 1 to 100:

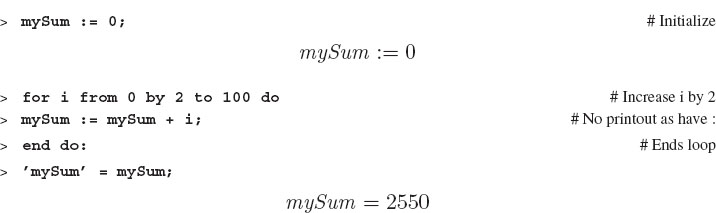
8.4.4 while Loop

You may not always know ahead of time just how often a loop must repeat before the necessary condition is met. In that case you repeat the loop while some condition is true:

while <expression> do <statements> end do

To give an instance, let us say we want to keep summing until some sum is greater than 10,000, and then find out what the i value is:

The problem with the while loop is that if the Boolean condition is always true, then the loop is “infinite”; that is, it never end. By way of example, if you change mySum < 10000 to mySum > 0, be prepared to press the stop button!

An addition to the while loop that will keep it from becoming infinite is to break the loop, that is, to stop it if some alternative condition is met (say, after 100,000 iterations). For example, here we break the previous while loop when i = 77:

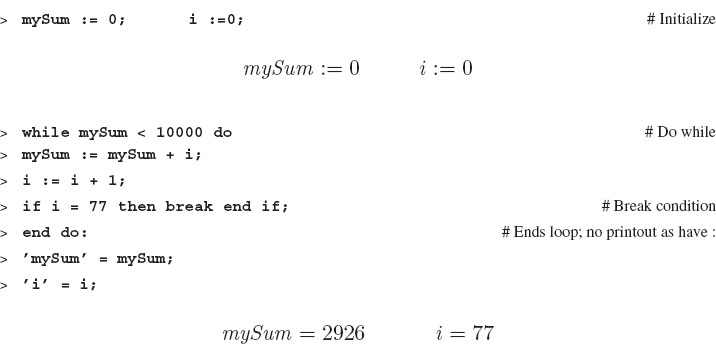
8.4.5 Procedures (Methods, Multiline Functions)

Though it is satisfying to write worksheets that have intelligence, the use of logic and looping tends to require many lines in order to handle all possible situations that may occur. If all the logic and possible cases are placed together, we may end up with a program that is so long and complicated that it is hard to follow. Consequently, it is useful to do some housekeeping and remove some of the utility commands out from the mainstream of our worksheets. Maple permits this by letting us define our own multiline procedures to be called from within a worksheet. Essentially, this is equivalent to defining a function, or what Java calls a method.

Here we define a procedure MySum() that sums the values of i from iStart to iEnd, and then uses Maple’s printf command to print out the results in a general format (the %g symbol). The definition of a procedure uses the Maple key word proc, takes the arguments iStart and iEnd, and ends with the key word end. Check over the absence of a semicolon or colon on the line containing proc, or on the last line before end:

MySum: = proc(iStart, iEnd)

local iQuit;

global i, mySum;

iQuit: = 77 ;

mySum: = 0 ;

for i from iStart to iEnd

do mySum: = mySum + i;

if i = iQuit then break

end if

end do;

printf(“ In MySum, at end of do loop, i = %g, mySum =%g”, i, mySum)

end proc

Observe that Maple returns a statement of what it thinks our procedure is intended to do, with italics used to indicate variable names.

Now we test our procedure by calling MySum, as you would any Maple function, with numerical values for the arguments iStart and iEnd. If the procedure works as intended, Maple should evaluate all the statements within the procedure and then return to the worksheet with values for the global variables:

Here we have called our procedure by name and supplied it with the required two arguments. The values for the internal, or local, variables within a procedure are not visible from the outside the procedure:

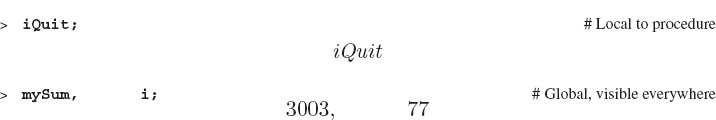
We see that the internal test causes the loop to break at i = 77, and that the value of the variable mySum does get returned to the calling program (it should, since we made it global). Now let us tell the procedure to end at iEnd = 70 and not give it a chance to break:

In summary, the general form of a procedure is:

where the first and last lines must always be present.

Exercise: Add the line > mySum: as the line before the > end; verify that now the value of mySum is returned.        ♠

8.4.6 Conversion of Procedures to Compiled Code

The code generation package CodeGeneration, and the older codegen, are used to convert Maple procedures and modules into compiled code. Although we give no examples, we tell you this for reference purposes.

8.5 SOLUTION: VOLUME FROM DIPSTICK HEIGHT

The solution to our problem requires us to solve for the height h at which

We start the solution by defining this function in Maple and then plotting it as a check that there are solutions in the region of interest:

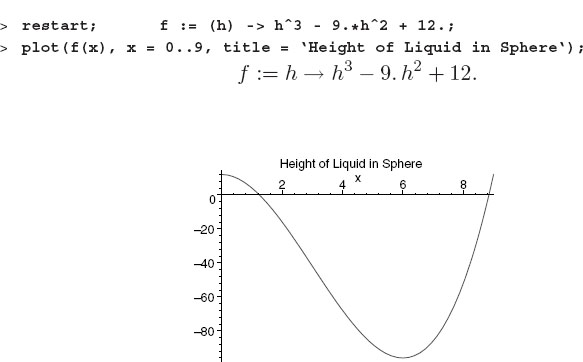
We observe two solutions, namely, two places where f(h) = 0. Yet as we discussed when we first set up this problem, the physical solution must lie in the range 0 < h < 2R = 6. Consequently only the root near h = 1.5 is physical.

As we said, while we have the option of using Maple’s fsolve to find the root, we will find it from scratch by programming up the bisection algorithm. We set the level of desired precision to eps = 0.01, and the range to search in as hhi = 7, hlo = 0:

We use a while loop to narrow down the h range until eps < (hhi — hlo)/(hhi + hlo) is no longer true:

This tells us that for a dipstick height h = 1.244m we have a volume V = 4π/3 = 4.19 m³ of fluid in the tank. As a check, we apply Maple’s fsolve command

Sure enough, we see that the two answers agree to one place in the fourth decimal place, just the precision we asked our algorithm to produce.

8.6 KEY WORDS AND CONCEPTS

Boolean expressions	Boolean variables	local vs. global	flow control	break
procedure vs. function	volume integration	logical operator	trial and error	loops

8.7 SUPPLEMENTARY EXERCISES