Chapter Ten

Data Types, Limits, Methods; Rocket Golf

10.1 PROBLEM AND THEORY (SAME AS CHAPTER 3)

Michele, our golf fanatic in Figure 3.1 is still in pursuit of the world’s record for the fastest golf ball. Recall, she hits her golf balls from a rocket moving to the right with a velocity v = c/2 relative to observer Ben on earth, and sees her ball travel with a speed of U = c/√3 at an angle θ = 30° with respect to the moving rocket. She observes her drive to remain in the air for hang time T’ = 2.6 × 10⁷ seconds.

The formulas we need from special relativity relate the description of the same moving object as it appears to observers in different frames. If Michele in O’ sees her golf ball having velocity components:

then Ben in O, who sees Michele moving to the right with velocity v, will see her golf ball move with velocity components

10.2 JAVA’S PRIMITIVE DATA TYPES

Before we begin to calculate with Java, it is in your best interest to explore the limitations of the numerical capabilities of Java. It all arises from the schemes

Table 10.1 Java’s basic data types and their sizes in bytes (B).

Name	Type	Bits	Bytes	Range & Precision
boolean	logical	1	-	true or false
char	string	16	2	’u0000’ ↔ ‘uFFFF’ (ISO Unicode)
byte	integer	8	1	–128 ↔ +127
short	integer	16	2	–32,768 ↔ +32,767
int	integer	32	4	–2, 147, 483,648 ↔ +2, 147, 483,648
long	integer	64	8	–9,223, 372,036, 854, 775,808 ↔
				9,223, 372, 036, 854, 775, 807
float	floating point	32	4	±1.401298 × 10 –45 ↔ ±3.402923 × 10+38
double	floating point	64	8	±4.94065645841246544 × 10-324 ↔ ±1.7976931348623157 × 10+308

Table 10.2 The use of three bits a, b, and c, to represent the eight integers from 0 to 2³ - 1 = 7.

Binary abc	= a × 22	+b×21	+c × 20	= Decimal
000	0	0	0	0
001	0	0	1	1
010	0	1	0	2
011	0	1	1	3
100	1	0	0	4
101	1	0	1	5
110	1	1	0	6
111	1	1	1	7

computers use to store information. As you have seen in Area.java’s statements containing int and double, Java is specific about the types of variable or data with which it deals. Variables are stored as any of Java’s primitive data types, or as ones you create yourself. The primitive data types and the amount of memory they occupy are described in Table 10.1. These are rather standard for most modern computer languages. Variables of these types are stored in the computer’s memory in small blocks of memory locations called words. The amount of memory used to store a variable depends upon what you want to store in the variable, and one of the chores you have in programming is deciding how long you want your variables to be. So, now a word about words.

10.2.1 Integers

The most elementary unit of memory is a little magnet, like a compass needle that points up or down. If we associate “down” with 0 and “up” with number 1, then we have a physical device that stores representations of 0’s and 1’s. It should then be no surprise to hear that all numbers on the computer are ultimately represented in binary form, namely, in terms of the binary digits (abbreviated bits) 0 and 1.

Just like the digits in the decimal system indicate the number of times that 10⁰, 10¹, 10²,…, are each contained in a number, so it is with the binary system. As an instance, in Table 10.2 we see the three bits abc representing the eight numbers from 0 to 7. Likewise, N bits are used to represent integers up to 2N. In practice, since the first bit is used to represent the sign of the integer, we effectively lose one bit, which means that it is possible to represent integers only up to 2N-¹ with N bits.

Long strings of 0’s and 1’s are fine for computers but awkward for people. Consequently, binary strings are converted to octal, decimal, or hexadecimal numbers before results are communicated to people. Octal and hexadecimal numbers are fine, but our decimal rules of arithmetic do not work for them, and so they are hard for humans to work with. Converting to decimal numbers makes the numbers easier for us to work with but usually causes some loss in precision.

The point of all this discussion about what goes on in the “guts” of memory is that in one way or another, you must tell Java how many bits you want to have assigned to store the value of each variable. The number of bits is called word length and is often expressed in bytes, where a byte is a “mouthful of bits”:

Conventionally, storage size is measured in bytes or kilobytes. For this reason, while one bit is adequate to represent a 0 or 1, two bytes are required to represent a single character, like the letter “a” or “b.”

In practice, 8 bits or 1 byte are used to store an integer, in which case the integers lie in the range 1-2⁷ or 1-128. More usually, 4 B = 32 bits are used for integers, which means that the maximum positive integer is 231 2 × 109. In spite of this seeming to be a large range for numbers, it really is not compared to the range of sizes encountered in the physical world. To illustrate, the ratio of the size of the universe to the size of a proton is 1040. Though Java integers have limited range, they are stored exactly on the computer if they are within this range.

Figure 10.1 An illustration of the limits of single-precision floating point numbers and the consequences of exceeding those limits.

10.2.2 Floating-Point Numbers

Scientific work primarily uses floating-point numbers. In floating-point notation, the number x is stored as a sign, a mantissa, and an exponent:

Here the mantissa contains the significant figures of the number, s is the sign bit, and the exponent permits very large, as well as very small, numbers.¹ To prove the point, a single-precision 32-bit word may allocate 8 bits of computer memory for the exponent in (10.6), which leaves 23 bits for the mantissa and 1 for the sign. This 8-bit integer “exponent” has the range [-127,128]. In practical terms this means that single-precision (4-byte) numbers have 6–7 decimal places of precision (1 part in 2²³) and magnitudes typically in the range

These ranges are represented schematically in Figure 10.1. If you write a program requesting double precision, then 64-bit (8-byte) words will be used in place of the 32-bit (4-byte) words. With 11 bits used for the exponent and 52 for the mantissa, double-precision numbers have about 16 decimal places of precision and typically have magnitudes in the range

10.2.3 Naming Convention

We have already seen with the program Area.java being stored in the file of the same name, that the name of a class file must match the name of the class. It is also conventional to have the name of the class start with a Capital letter, as we did with Area.java.

Regular variables in Java usually are written with lowercase letters. Even though a variable may start with a lowercase letter, it may contain capital letters within, such as hiMass and loMass. Variable names may contain alphanumeric (letters and numbers) characters and underscore characters () but must start with a letter or an underscore. All names are case sensitive, so IloveYou and ILOVEYou are completely unrelated. We have also seen PI spelled with all capital letters. If a piece of variable does not change as the program runs, then it is a constant or a FINAL and is denoted by all capital letters. Finally, it is illegal to use as names those words that Java has reserved for itself:

Reserved Words

abstract	boolean	break	byte	case	catch	char
class	const	continue	double	default	do	else
extends	final	finally	float	for	goto	if
import	implements	instanceof	int	interface	long	native
new	null	package	private	protected	public	return
short	static	super	switch	synchronized	this	throw
throws	transient	try	void	volatile	while

Examples of acceptable names are:

AlbertEinstein, alEinstein, F B I, Herr Prof Dr, Geo3rd

Examples of unacceptable (space, special character, reserved word, beginning number) names are:

Al Einstein, Al*Einstein, final, 3rdGeo

10.2.4 Machine Precision

One consequence of computers using the floating-point representation to store numbers is that most numbers are stored with only a limited precision. We see a schematic representation of this in Figure 10.1, where you are to imagine floatingpoint numbers being stored along the vertical hash marks. If you call for a number that lies between the hash mark, the computer will move you to the closest number. The corresponding loss of precision is called truncation error.

The exact precision obtained in a calculation depends on the program. For a single operation, single precision usually yields 6–7 decimal places for a 32-bit word, and double precision 15–16 places. To understand how machine precision affects calculations, what would you guess is the result of the simple addition of two single-precision numbers: 7 + 2.0×10-⁸?

The correct answer is (c). Because there is no more room left to store the 2.0 × 10-8, it is lost or truncated from the answer, and the addition gives 7.

This loss of precision is categorized by defining the machine precision em as the maximum positive number that may be added to the number stored as 1 without changing the number stored as 1 on the computer:a

Here the subscript c is a reminder that the variable is the number stored in the computer’s memory. Likewise, xc, the computer’s representation of an arbitrary number x, and the actual number x, are related by

Remember, ε_m ~ 10^-7 for single precision and ε_m ~ 10^-16 for double precision.

10.2.5 Under- and Overflows

If a single-precision number x is larger than 2¹²⁸, an overflow occurs. If x is smaller than 2-¹⁴⁹, an underflow occurs. We visualize this in Figure 10.1 by observing that any number that tries to get closer to 0 than 10-⁴⁵ in magnitude falls in the gray region at the center, and leads to underflow. Likewise, any number whose magnitude exceeds 10⁺³⁸ falls in the gray region at the ends of the line, and leads to overflow. The number xc that the computer stores may end up being NAN (not a number), or a noncomputable infinity, or zero. Because underflow is a loss of information, a scientific programmer should be sensitive to its occurrence. Because the only difference between the representations of positive and negative numbers on the computer is the one sign bit for negative numbers, the same considerations hold for negative numbers.

In our experience, serious scientific calculations almost always require double precision (8B). And if you need double precision in one part of your calculation, you probably need it all over, and that also means double-precision library routines. If you want to be a scientist or an engineer, learn to say “no” to singles and floats.

Listing 10.1 Limits.java

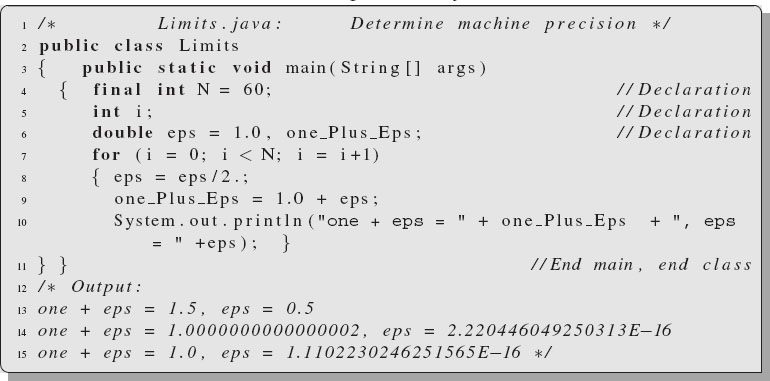
10.2.6 Experiment: Determine Your Machine’s Precision

Listing 10.1 contains the small, but significant, program Limits.java for you to “test-drive” during your “break-in” period with Java. By repeatedly comparing 1+ em to 1 as em is made smaller, Limits.java determines the machine precision as the value of em for which the variable onePlusEps equals 1:

10.3 METHODS (FUNCTIONS) AND MODULAR PROGRAMMING

On the left of Figure 10.2 we show a simple Java program. The class’s name is Golf and in it is the class definition and the main method. The only conceptual advance beyond the Area.java program of Chapter 9 is that we have included the definition of class variable in the box indicating the class definition public class Golf. Class variables are defined just like any other variable, except by doing it at the class level, they may be used by all methods. Variables defined within methods are local to that method.

In some ways, having a small program like Area.java do all its computing in the main method makes sense. Because execution begins there, you may as well put all the work there so you do not have to look elsewhere to find it. As programs get called on to do more, they tend to get more complicated and harder to follow or modify. Then it makes sense to adopt a modular approach in which a program is divided into several relatively small subprograms, with each subprogram having its own separate function.

In Java, the separate subprograms are separate methods and are usually placed within a class of related methods. Often each class has its own main method to begin execution, but that is not necessary. This collection of data (variables) and methods used to manipulate those data is the abstract definition of class.

It is a great idea to save time and not repeat yourself, and so it is also possible for methods in one class to call methods from other classes. As an example, the mathematical functions, to be discussed shortly, are in the class named Math. We call the method sin in that class just by adding a prefix to the method name; for example, Math.sin.

On the right of Figure 10.2 we show an example where we have enlarged the class Golf to now contain the methods Uy and gamma as well as main. The main method may call either of the other methods, and the other methods can call each other as well, but not main. Data is transferred in these calls by means of the argument list and the value of the method (input and output), as well as through the class variables, which may be shared by all methods.

There are many good reasons for writing a program in which there are multiple methods with each method performing a single task (modular programming). This lets us build up into complexity with individual modules that are to be written and tested separately, reused in a number of programs, and in which the logic of the program is easy to follow. In good modular programming design, the main method is the control unit, or administrator, of the program, and it calls other methods to get the work done without doing any of the work itself. So you get a good idea of what an entire program does just by reading through its main method; the details are left to the other methods.

Listing 10.2 Method.java

Enough theory! Now some concrete examples. In Listing10.2 is the program Method.java, containing a main method and a single auxiliary method. The program prints out 100 values of i and the function f(i) = sin(i) + 1 to the computer screen. Observe how the name of the method f is returned as the value of the function. This permits us to use it on line 7 as fVal = f(i).

Also observe that the method f is called with the argument i in main, yet is defined with the argument y in the f method. This is fine. Whereas it is important that the data types of the arguments agree in main and in f, the variable names are local to each method and do not have to agree. When the program is executed, actual numbers get passed between main and f (a value pass), and not the variable names (a reference pass).

Find this program on the disk, copy it to your personal directory, and compile and execute it. Make sure that the name of the file Method.java matches the name of the class. After compilation, there will be another file Method.class containing the compiled byte code. The names of the individual methods do not appear, only the name of the class.

One of the confusing aspects of first learning about methods is that their names seem to be surrounded by so much “junk.” Just as you learn to read a newspaper without ever looking at any of the advertisements, so you soon will be able to make sense out of these methods without letting the junk get in your way. The junk arises from the fact that the Java compiler needs to be told in advance what kind of variables will be input and output to a method, and so it requires you to place a whole slew of modifiers in front of and after the method name. As a case in point, when we declared a method on line 10

we are just saying that there will be a function f(y) that takes as input the integer y and returns a double for f(y). The public modifier is for access control and means that this method is visible everywhere. The static modifier is related to the object-oriented aspects of Java (to be discussed later) and implies that this method is not dynamic so that it may be accessed from the main method.

10.3.1 Main Method

We almost always declare a main method with

Table 10.3 Java’s mathematical functions.

Math	Java	Math	Java	Math	Java
e (lne = 1)	Math.E	π	Math.PI	xy	pow(x,y)
sin θ	sin(q)	cos θ	cos(q)	tan θ	tan(q)
sin-1 θ	asin(q)	cos-1 θ	acos(q)	tan-1 θ	atan(q)
tan-1(y/x)	atan2(x, y)	ex	exp(x)	ln x	log(x)
random #	random()	√ x	sqrt(x)	x	abs(x)
remainder	IEEEremainder(x,y)	max(x, y)	max(x,y)	min(x, y)	min(x,y)
next integer	ceil(x)	previous int	floor(x)	max(x, y)	max(x,y)
nearest integer	double rint(x)	nearest int	round(x)	min(x, y)	min(x,y)

The modifier static before main indicates that main is a static method and not dynamic like an object. We talk about objects in Chapters 16 and 18 and suggest you ignore it for now. The modifier void before main indicates the type of output produced by main, in this case nothing (remember, main is an administrator that just watches over the work done by others). Likewise, the parentheses in main(String[] argv) contain the input or arguments supplied to main. In this case there is a single argument named argv and it is a String. The square brackets [ ] indicate that argv is an array, namely, a subscripted variable. Even though the argument to the main method may look rather complicated, the good news is that you do not have to supply the argument; String argv[] is passed to the main method by the Java interpreter when you run the program.

10.3.2 Mathematical Methods

Java contains a Math library or package that knows how to compute numerical values for a whole bunch of functions. This collection of methods has the official name java.lang.Math. To use a method from this package, for example, cos the cos function, you need to tell Java where to find it. It this case you could say java.lang.Math.cos or be lazy and use the nickname Math.cos. Other examples include Math.sin(x) and Math.sin(Math.PI), where Math.PI is the numerical value of π. Table 10.3 gives Java’s mathematics functions. They all need the Math. prefix to work. In most cases, the functions take and return various argument types, such as doubles and floats.

Exercises: Compile and execute the program TestMath.java in Listing 10.3 and make sense out of its error message. Replace the x assignment statement in the program with each of the following and note the results:

Listing 10.3 TestMath.java

Regardless of the built-in math functions giving accurate answers, they do not know everything about mathematics and will give error messages or nonnumeric answers if pushed too far. Take the previous TestMath program and use it to evaluate:

10.4 SOLUTION: VIEWING ROCKET GOLF

We will now use Java to solve the same Rocket Golf problem as we did with Maple in Chapter 3. The application of modular programming means that we will now write separate methods, as we did with Maple’s user-defined functions, to compute γ, Ux, and Uy, and plot a graph of γ versus v using PtPlot.² Our solution program thus contains a main method, three computational methods, and one plotting method. To determine how round-off error affects the results, we describe and run the program that solves the problem in double precision and ask you to modify it so that it solves the same problem in single precision with floats (we give the results of both, but the source for only double precision).

Listing 10.4 shows the class Golf.java. It takes as input data the angle and velocity of Michele’s golf ball and computes the velocities and angles as seen by Ben. If you set the speed of light c equal to a nearly infinite number, the relativistic effects vanish. Observe that we have placed the main method at the top and followed it by the four methods gamma, Ux, Uy, and plotGamma. We like the main method to go first, as it shows from the start how the program works. This is top-down programming. Some programmers prefer defining all the methods first before they are called. That is bottom-up programming. The Java compiler does not care if you call a method before it is defined; as long as it is defined somewhere within the class file (or in other class files that get included), there will be no error messages.

Listing 10.4 Golf.java

Figure 10.3 A plot of the function γ(v) output from the program Golf.java using PtPlot. Compare to Maple’s plot in Chapter 3.

Find where the method Uy calls the method gamma. Having one method call another is good modular programming practice. Also note that we have kept the program neat by placing all the plotting commands in the method plotGamma. We thereby keep the technical details from interfering with our ability to see the logical flow of the program, and we permit ourselves to modify the plotting without messing up the rest of the program. The plot obtained is shown in Figure 10.3 and looks much like the Maple plot in Chapter 3.

When comparing the double (ours) and float (your) versions of this program, it is interesting to observe that it is simpler to write Java programs in doubles than floats. The simplicity of doubles is a consequence of Java automatically treating numerical constants as doubles and converting mixed singles plus doubles into doubles, of the math library automatically doing its computations in double precision, and of Java not permitting you to decrease precision (say from double to float) without your acknowledging the fact.

To create a float version of the program, you will have to convert doubles into singles with the cast operator (float) and add an F to numerical constants,

Table 10.4 Results of double- and single-precision computations.

Golf.java: double methods	GolfFloat.java: float methods
T = 3.1843366656181317E7 s	T = 3.1843364E7 s
ux = 0.8	ux = 0.8
uy = 0.19999999999999996	uy = 0.2
u = 0.8246211251235323	u = 0.82462114
phi = 0.24497866312686412	phi = 0.24497867

Table 10.5 Results of double- and single-precision computations for the second case.

Golf.java: double methods	GolfFloat.java: float methods
T = 3.1843366656181317E7 s	T = 3.1843364E7 s
ux = -1.4802973661668753E-16	ux = 3.973643E-8
uy = 0.33333333333333326	uy = 0.33333337
u = 0.33333333333333326	u = 0.33333337
phi = 1.5707963267948972	phi = 1.5707963

such as in 1.0F -v * v, so they are stored as floats:

9 v = 0.5F;

10 theta = (float) (30.0 * Math.PI/180.0);

The output we obtained for the two cases is compared in Table 10.4. Take stock of how Java prints out only one digit beyond the decimal point, such as in ux = 0.8, as its way of telling you that as far as it knows all other digits beyond the decimal point are zero. This a Java solution to the first part of the problem, where Michele hits the golf ball forward. We see that Java is smart enough to realize that its single-precision calculation with floats has 6–7 places of precision, and so prints out just 8 significant figures (an extra 1 or 2 places so you are able to see the imprecision). In contrast, Java prints out 17 significant figures for doubles, where we expect 15–16 places of precision.

In the second part of the problem, Michele hits the golf ball backward (at θ = 150°). To find a solution to this part of the problem, we will have to modify the program. We changed the line theta = 30.0 * Math.PI / 180.0; so that it now reads

theta = 150.0 * Math.PI / 180.0;

When we ran the modified program we obtained the output in Table 10.5. In these cases we are subtracting two numbers of nearly equal value and so should expect a significant loss of precision. If we look at a number such as u for the backward golf ball (which involves subtractions and is more sensitive), we see

u = 0.33333333333333326    u = 0.33333337

The above values are clearly the level of precision (size of error) we would expect for a single- and double-precision floating-point calculation: 1 unit in the 16th place for doubles, and 4 units in the 8th place for singles. Even though Maple could do this computation exactly and obtain 1/3 as the answer, that is not possible with the approximate floating-point representation of numbers used in numeric computations.

When we solve the third part of the problem and look at the x component of velocity that Ben sees for the backward hit, we find that the double- and singleprecision calculations give:

ux = -1.4802973661668753E-16    ux = 3.973643E-8

Within the precision of the calculation, the x velocity is zero. It is not exactly zero, because the numbers used in the calculation are stored with limited precision. We see that it is very hard for floating-point computations to compute exactly zero.

10.4.1 Assessment

One way of interpreting these numbers is to say that the double-precision computation has an error in the 16th decimal place, while the single-precision computation has an error in the 8th place. This is as expected. A more negative way of interpreting these same numbers is to say that the two computations cannot even agree on the sign of the velocity, or to say that the floating-point calculation is wrong by a factor of a million! We personally would say that since the velocity predicted by the program is much smaller than the velocities we used as input, we clearly should suspect the precision of the output. In the present case, we would say that both answers appear consistent with zero, yet we do not believe that we have even one significant figure in the answer.

10.5 YOUR PROBLEM: MODIFY GOLF.JAVA

10.6 COERCION AND OVERLOADING*

We have already told you (and you have probably forgotten) that when you call a method the actual value of the argument is passed to the methods from the calling program. Remember, main sends only a number to the method, not the name of the argument. On account of this it is quite acceptable to call a method with the variable x as the argument to the method, and then use a different variable like y as the argument within the actual method itself. As a general rule, methods may change the value of their argument, but may not change the location in memory to which the argument refers.

The program Change.java in Listing 10.5 is short but with surprising results:

Listing 10.5 Change.java

10.7 KEY WORDS

[]	array	binary numbers	bits
bytes	class	class variables	argument coercion
local variables	machine precision	memory words	method overload
modular programs	naming convention	overflow	primitive data type
significant figures	double precision	underflow	variable casting
word length

10.8 SUPPLEMENTARY EXERCISES

1In practice a number called the bias is subtracted from the exponent exp so that the stored exponent is always positive.

2We describe the use of PtPlot in Chapter 11. We recommend that you read that chapter soon; however, you may work through the present sections just by copying the plotting commands.