3.02.2.1 AIC and the stepwise regression

Previously, we noticed that minimizing cannot be used as the criterion. An intuitive approach is to introduce an additive term that penalizes overfitting. The penalty term needs to be an increasing function of , so that the criterion −2  (maximum log-likelihood) decreases as the penalty term increases yielding a trade-off between goodness of fit and simplicity. This principle of parsimony is the fundamental idea of model selection. As we shall see, the classic approximations of information criteria reduce to such forms. For example, the AIC can be stated as

that is, , and the regression model (hypothesis ) that minimize the criterion is chosen. Here, the penalty term is which increases with and hence penalizes selecting too many variables. In the regression setting,

where we have suppressed the irrelevant additive constant N from (2.2) and the “plus one” term from which does not depend on the number of explanatory variables in the model. Note that the robust versions of AIC have been proposed, e.g., [21] which utilizes robust M-estimation.

The AIC is not computationally feasible for variable selection when the number of explanatory variable candidates k is large. We need to consider all index sets I of size for each and for each m, there are possible index sets. More practical and commonly used approach is to use stepwise regression variable selection method. In the forward stepwise search strategy one starts with a model containing only an intercept term (or a subset of explanatory variables), and then includes the variable that yields the largest reduction in the AIC, i.e., the largest reduction in the RSS (and thus improving the fit the most). One stops when no variable produces a normalized reduction greater than a threshold. There are several variants of stepwise regression which differ based on the criterion used for inclusion/exclusion of variables. For example, instead of AIC, Mallows Cp, BIC, etc. can be used. One particularly simple stepwise regression is to include in each step the variable that is most correlated with the current residual , where is the LS fit based on the current selection of variables. This strategy is called the orthogonal matching pursuit[22] in the engineering literature. Some modern approaches for variable selection in regression that can be related to the forward stepwise regression are the LASSO (least absolute shrinkage and selection operator) [23] and the LARS (least angle regression) [24]. LASSO minimizes the usual LS criterion (the sum of squared residuals) with an additional -norm constraint on the regression coefficient. As a result, some regression coefficients are shrunk to(wards) zero. LARS is a forward stepwise regression method where the selection of variables is done differently: namely a regression coefficient of the variable is increased until that variable is no longer the one most correlated with the residual r. A simple modification of the LARS algorithm can be used to compute the LASSO solution [24].

3.02.2.2 Cross-validation and bootstrap methods

Cross-validation (CV) is a widely used technique for model order selection in machine learning, regression analysis, pattern recognition, and density estimation; see [25]. In CV one is interested in not only finding a statistical model for the observed data but also in prediction performance for other independent data sets. The goal is to ensure that the model generalizes well, not adapting too much to the particular data set at hand. Unlike many other model selection techniques, CV can be considered a computer-based heuristic method that replaces some statistical analyses by repeated computations over subsets of data.

In CV, one splits the data set into subsets, one training set for the initial statistical analysis and the other (potentially multiple) subsets for testing or validating the analysis. If the test data are independent and identically distributed (i.i.d.), they can be viewed as new data in prediction. If the sample size for the training set is small or the dimension of the initial model is high, it is likely that the obtained model will fit the set of observations with too high fidelity. Obviously, this specific model will not fit the other test data sets equally well and the prediction estimates produced by the initial model using the training set may contain significantly off-values than expected ones.

The prediction results from the testing (validation) sets are used to evaluate the goodness of the model optimized for the training set. The original model may then be adjusted by combining with the models estimated from the test sets to produce a single model, for example by averaging. CV may also be used in cases where the response is indicator of a class membership instead of being continuous valued. This is the case in M-ary detection problems and pattern recognition, for example.

There are many ways to subdivide the data into training and test sets. The assignment may be random such that the training set and the test set have equal number of observations. These two data sets may be used for training and testing in an alternating manner. A very commonly used approach is so-called leave-one-out (LOO) cross-validation. Each individual observation in the data set is serving a test set at its turn while the remaining data form the training set. This is done exhaustively until all the observations have been used as a test set. It is obvious that LOO has a high computational complexity since the training set is different and training process is repeated every time.

Cross-validation can also be used for model order selection in regression. Let us assume that we have a “supermodel” of large number of explaining variables and we want to select which subset of explaining or predictor variables gives the best model in terms of its prediction performance. By using the cross-validation approach with the test sets of observations one may find a subset of explaining variables that gives the best prediction performance measured, for example, in terms of mean square error. If cross-validation is not used, adding more predictor variables in the model decreases the risk or error measure, such as mean square error, sum of squared residuals or classification error for the training set but the predictive performance may be very different.

A few remarks on the statistical performance of the CV method are in place. CV gives a too positive view on the quality of the model optimized for the training set. The risk or error measure such as MSE will be smaller for the training set than the one for the test set. The variance of the cross-validation estimates depends on the data splitting scheme and it is difficult to analyze the performance of the method in a general case. However, it has been established in some special cases, see [25]. If the model is estimated for each subset of test data, the values of estimates will vary (estimator is a random variable).

The CV estimators often have some bias that depends on the size of the training sample relative to the whole sample size. It tends to decrease as the training sample size increases. For the same size of training set the bias remains the same but differences may be attested in variance (accuracy). The overall performance of the CV estimators depends on many factors including the size of training data set, validation data set, and the number of data subsets.

Bootstrapping [26] is a resampling method that is typically used for characterizing confidence intervals. It has found applications in hypothesis testing and model order estimation as well, see, e.g., [27]. Assuming independent and identically distributed (i.i.d.) data samples, it resamples the observed data set with replacement to simulate new data called bootstrap data. Then the parameter of interest such as the variance or the mean is computed for the bootstrap sample. It is a computer-based method since it requires that a very large number of resamples are drawn, and bootstrap estimates for each bootstrap sample are computed. Availability of highly powerful computing machinery has made the use of bootstrap more feasible in different applications as well as allowed to increase the sample sizes. The bootstrap method does not make any assumptions on the underlying distribution of the observed data. It is a nonparametric method and allows for characterizing the distribution of the observed data. This is particularly useful for non-Gaussian data where the distribution may not be symmetric or unimodal. An example of model order estimation in a sensor array signal processing application is provided in [27].

3.02.3.1 Bayesian Information Criterion (BIC)

We start by recalling the steps and assumptions that lead to the classic asymptotic approximation of BIC due to Schwarz [7] which can be stated as follows:

so that and the hypothesis (mth model) that minimizes the criterion is to be chosen. This approximation is based on the second-order Taylor expansion of the log posterior density and some regularity assumptions on the log-likelihood and log posterior. Recall from earlier discussion on the nested hypotheses, the term −2  (maximum log-likelihood) monotonically decreases with an increasing m (model index), and cannot be used alone as it leads to the choice of the model with the largest number of parameters. The second term is the penalty term that increases with and hence penalizes the use of too many parameters.

In the Bayesian framework, the parameter vector is taken to be a random vector (r.v.) with a prior density . For the mth model, let

denote the log posterior density (neglecting the irrelevant additive constant term). The full BIC is obtained by integrating out the nuisance variable in the posterior density of given the data y and the model m:

(2.3)

The mth model that maximizes over is selected for the data. In most cases, the integration cannot be solved in a closed-form and approximations are sought for.

In Bayesian approach, the maximum-a-posteriori probability (MAP) estimate is a natural point estimate of and assume that it is unique. An approximation of around the MAP estimate based on second-order Taylor expansion yields

Note that the first-order term vanishes when evaluated at the maximum. Let us assume that is twice continuously differentiable (). This means that its second-order partial derivatives w.r.t. exist on and that the resulting (negative) Hessian matrix is symmetric. Substituting the approximation into (2.3) yields

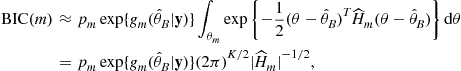
where the last equality follows by noticing that the integrand is the density of -variate distribution up to a constant term , where denotes the matrix determinant. Equivalently, we can minimize the log of BIC. In logarithmic form, the BIC becomes

(2.4)

An alternative approximation for the BIC can be derived with the following assumption:

Due to (A), when evaluating the integral in (2.3), we may extract the term from the integrand as a constant proportional to , yielding the approximation

(2.5)

(2.6)

where is the Fisher information matrix of the mth model evaluated at the unique MLE . Note that (2.6) is an approximation of (2.5) using (similarly as earlier) the second-order Taylor expansion on around the MLE. Thus in terms of logarithms, we have

(2.7)

Note that approximations (2.4) and (2.7) differ as the former (resp. the latter) is obtained for the case that the full log posterior (resp. log-likelihood) is expanded to the second-order terms. Furthermore, (2.7) relies upon (A).

Next, note that under some regularity conditions and due to consistency of the MLE , we can in most cases approximate for a sufficiently large N as

(2.8)

Since the three first terms in (2.7) are independent of N [recall assumption (A)], we may neglect the first three terms in (2.7) for large N, yielding after multiplying by the earlier stated classic approximation due to Schwarz,

(2.9)

Let us recall the assumptions for the above result. First of all, the log-likelihood function ought to be a -function around the neighborhood of the unique MLE . Second, the prior density is assumed to verify Assumption (A). Third, sufficient regularity conditions based on likelihood theory, e.g., consistency of , are needed for the approximation (2.8) to hold. Note that the classic BIC approximation, in contrast to approximations (2.4) or (2.7), is based on asymptotic arguments, i.e., N is assumed to be sufficiently large. Naturally, how large N is required, depends on the application at hand. The benefit of such an approximation is its simplicity and good performance observed in many applications. As we shall see in Section 3.02.4, Rissanen’s MDL derived using arguments in coding theory can be asymptotically approximated in the same form as BIC in (2.9). This sometimes leads to misunderstanding that MDL and BIC are the same.

If we assume that the set of hypotheses includes the true model that generated the data, then the probability that the true th model is selected can often be calculated analytically. For example, in the regression setting, the BIC estimate has proven to be consistent [28], that is, as . This can be contrasted with the AIC estimate that fails to be consistent, due to a tendency of overfitting [28].

3.02.3.2 GLRT-based sequential hypothesis testing

Let us assume that sequence of model p.d.f.’s , belong to the same parametric family (i.e., share the same functional form, so for ) and are ordered in the sense that . Hence, we have a nested set of hypotheses . We can consider as the “full model” and , a parsimonious model presuming that a subset of the parameters of the full model are equal to zero. This type of situation can arise in many engineering applications; a practical application is given in Section 3.02.5. In such a scenario, the GLRT statistic, defined as the the log of the ratio of the likelihood functions maximized under and under the full model :

(2.10)

where and and denotes the log-likelihood. By the general maximum likelihood theory, has a distribution asymptotically (i.e., chi-squared distribution with degrees of freedom), where

The null hypothesis is rejected if exceeds a rejection threshold , where is th quantile of the distribution (i.e., when ). Such a detector has an asymptotic probability of false alarm (PFA) equal to . For example, choosing PFA equal to is quite reasonable for many applications; however, in radar applications, smaller PFA is often desired.

The sequential GLRT-based model selection procedure chooses the first hypothesis (and hence as the model order) that is not rejected by the GLRT statistic. In other words, we first test and if it is rejected by the GLRT statistic (2.10) ( for some predetermined PFA ), then test , etc. until acceptance, i.e., until . In case that all hypotheses are rejected, then we accept the full model . Note that the above decision sequence is not statistically independent, even asymptotically. Hence, even though the asymptotic PFA of each individual GLRT for testing is , it does not mean that the asymptotic PFA of the GLRT-based model selection is . It is also possible to use a backward testing strategy, i.e., test the sequence of hypotheses from the reverse direction. Then we select the model in the sequence before the first rejection. That is, we first test and if it is accepted, then test . Continue until the first rejection and select the hypothesis tested prior the rejection. If it is known a priori that a large model order is more likely than a small model order, then the backward strategy might be preferred from pure computational point of view.

3.02.4.1 Akaike Information Criterion (AIC)

The AIC criterion is based on an asymptotic approximation of the K-L divergence. Let denote the true p.d.f. of the data and let denote the approximating model. The Kullback-Leibler (K-L) divergence (or relative entropy), can be defined as the integral (as f and are continuous functions)

and it can be viewed as the information loss when the model f is used to approximate or as a “distance” (discrepancy) between f and since it verifies

Clearly, among the models in the set of hypotheses , the best one loses the least information (have smallest value of ) relative to the other models. Note that the K-L divergence can be expressed as

where the model dependent part is . When finding the minimum of over the set of models considered is equivalent to finding the maximum of the function

among all the models. The function , sometimes referred to as relative K-L information, cannot be used directly in model selection because it requires the full knowledge of the true data p.d.f. and the true value of the parameter in the approximate model , both of which are unknown. Hence we settle with its estimate

(2.11)

where w is an (imaginary) independent data vector from the same unknown true distribution as the observed data y and denotes the MLE of based on the assumed model f and the data y. Note that the statistical expectations above are w.r.t. to the true (unknown) p.d.f. and we maximize (2.11) instead of . Key finding is that for a large sample size N, the maximized log-likelihood is a biased estimate of (2.11) where the bias is approximately equal to , the number of the estimable parameters in the model. The maximum log-likelihood corrected by the asymptotic bias, i.e., , can be viewed (under regularity conditions) as an unbiased estimator of when N is large. Multiplying by gives the famous Akaike’s Information Criterion

Unlike the BIC, the AIC is not consistent, namely the probability of correctly identifying the true model does not converge to one with the sample length. It can be shown that for nested hypotheses and under fairly general conditions,

that is, AIC tends to overfit, i.e., choosing model order that is larger then the true model order. See, e.g., [15].

Some enhanced versions have been introduced where the penalty term is larger to reduce the chance of overfitting. The following corrected AIC rule [29,30]

(2.12)

(2.13)

provides a finite sample (second-order bias correction) adjustment to AIC; asymptotically they are the same since when , but for finite N. Consequently the penalty term of is always larger than that of AIC, which means that the criterion is less likely to overfit. On the other hand, this comes with an increased risk of underfitting, i.e., choosing a smaller model order than the true one. Since the underfitting risk does not seem to be unduly large in many practical experiments, many researchers recommend the use of instead of AIC. It should be noted, however, that possess a sound theoretical justification only in the regression model with normal errors, where it is an unbiased estimate of the relative K-L information; note that AIC is by its construction only an asymptotically unbiased estimate of the relative K-L information. Besides the regression model, the reasonings for , lay merely on its property of reducing the risk of overfitting. The so-called generalized information criteria (GIC) [2], defined as in (2.13) as

can often outperform AIC for . For example, when the is obtained and the choice yields the MDL criterion.

3.02.4.2 Minimum Description Length

The Minimum Description Length [11] method stems from the algorithmic information and coding theory. The basic idea is to find any regularity in the observed data that can be used to compress the data. This allows for condensing the data so that less symbols are needed to present it. The code used for compressing the data should be such that the total length (in bits) of description of the code and the description of the data is minimal. There exists a simple and refined version of the MDL method. The concept of stochastic complexity will be employed in estimating the model order. It defines the code length of the data with respect to the employed probability distribution model. It also establishes a connection to statistical model order estimation methods such as BIC and MDL. In some special cases, the approximation of stochastic complexity and BIC leads to the same criterion. Detailed descriptions of the MDL method can be found in [1,4].

The MDL method does not make any assumptions on the underlying distribution of the data. In fact, it is considered to be less important since the task at hand is not to estimate the distribution that generated the data but rather to extract useful information or model from the data that facilitates by compressing it efficiently. However, codes used for compressing data and the probability mass functions are related. The Kraft inequality establishes a correspondence between code lengths and probabilities whereas the information inequality relates the optimal code in terms of the minimum expected code length with the distribution of the data. If the data obeys the distribution , then the code with the length achieves the minimum code length on average.

A simple version of the MDL principle may now be stated as follows. Let be a class of candidate models or codes used to explain the data y. The best model is the one that minimizes

i.e., the sum of the length of the description of the model and the length of the data encoded using the model. Trading-off between complexity of the code and complexity of the data is built in the MDL method. Hence, it is less likely to overestimate the model order and overfit the data than AIC, for example.

A probability distribution where the parameter may vary defines a family of distributions. The task of interest is to optimally encode the data and to use the whole family of distributions in order to make the process efficient. An obvious choice from the distribution family would be to use the code corresponding to where is the MLE of for the observed data, i.e., that most likely would have produced the data set. Consequently, the code corresponding to the maximum likelihood (or the probability model) depends on the data and the code cannot be specified before observing the data. This makes this approach less practical. One could avoid this problem by using an universal distribution model that is representative of the entire family of distributions and would allow coding the data set almost as efficiently as the code associated with the maximum likelihood function. The refined MDL uses normalized maximum likelihood approach for finding an universal distribution model used to assist the coding. This will lead to an excessive code length that is often called regret. The Kullback-Leibler divergence may be used as a starting point where p is employed to approximate the distribution f. Finding the optimal universal distribution can be formulated as a minimax problem:

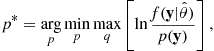
where q denotes the set of all feasible distributions. The distribution represents the worst case approximation of the maximum likelihood code and it is allowed to be almost any distribution within a model class of feasible distributions. Hence, the assumption on the true distribution generating the data may be considered to be relaxed. The so-called normalized maximum likelihood (NML) distribution satisfies the above optimization problem. It may be written as [31]

where denotes the maximum likelihood estimate of over the observation set. The denominator is a normalizing factor that is the sum of the maximum likelihoods of all potential observation sets Y acquired in experiments, and the numerator represents the maximized likelihood value. With this solution, the worst case data regret is minimized. It has been further shown that by solving a related minimax problem

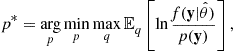
the worst case of the expected regret is considered instead of the regret for the observed data set, see [32].

The code length associated with normalized maximum likelihood is called the stochastic complexity of the data for a distribution family. It minimizes the worst case expected regret

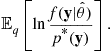
The MDL method employs first the normalized maximum likelihood distributions to order the candidate models and chooses the model that gives minimal stochastic complexity. An early result by Rissanen [11] and a frequently used approximation for the stochastic complexity is given as follows:

which is the same result as the approximation of BIC by Schwarz given earlier in this section. Other approximations of the stochastic complexity that are more accurate avoid some pitfalls of the above approximation, for example:

where denotes the Fischer information matrix of sample size 1. The term contains the higher order terms and vanishes as . The integral term with Fischer information needs to be finite. See [33] for more detail on other approximations and their computation. The MDL principle and the normalized maximum likelihood (NML) lead to the same expression as the Bayesian Information Criterion (BIC) in some special cases, for example, when Jeffrey’s noninformative prior is used in a Bayesian model and . In general, however, the NML and BIC have different formulations. The MDL has been shown to provide consistent estimates of the model order, e.g., for estimating the dimensionality of the signal subspace in the presence of white noise [34]. This problem is reviewed in detail in the next section.