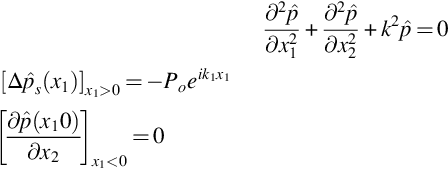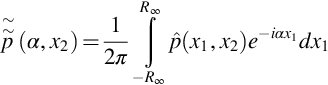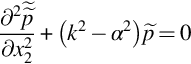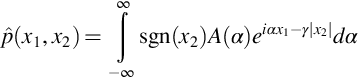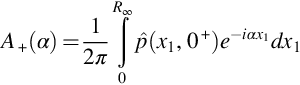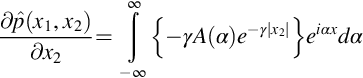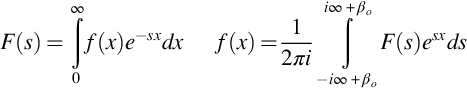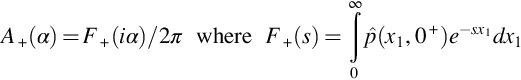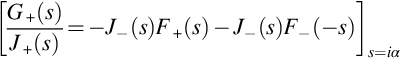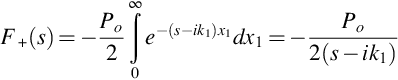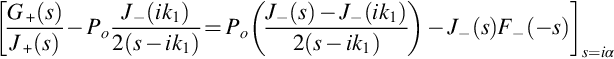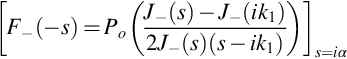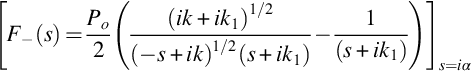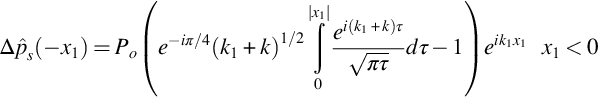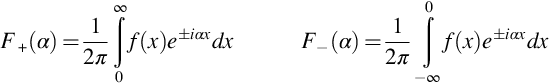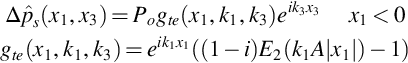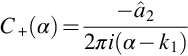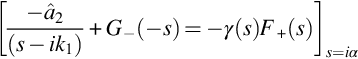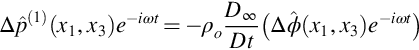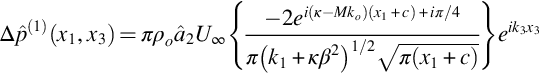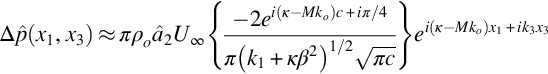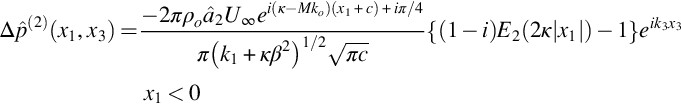13.2 The Schwartzschild problem and its solution based on the Weiner Hopf method

13.2.1 The boundary value problem

The scattering of hydrodynamic pressure waves by a trailing edge can be modeled by considering a surface pressure disturbance traveling downstream over a semi-infinite plate, as shown in Fig. 13.1. The disturbance is expressed in terms of Δp, the pressure difference between the top and bottom sides of the plate.

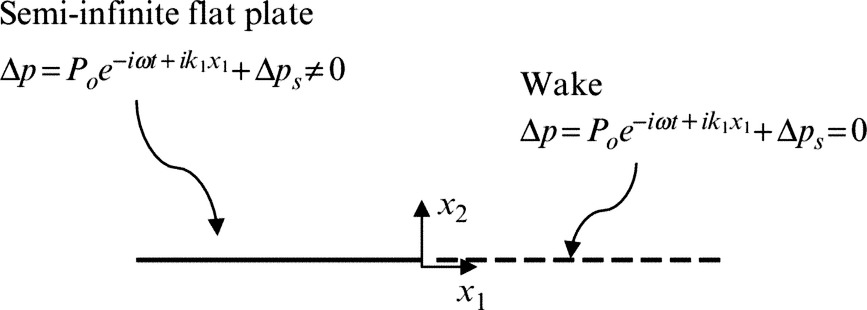
We assume that the pressure jump Δp in the absence of the trailing edge (located at x₁=0) is given by P_oexp(−iωt+ik₁x₁) and that the flow Mach number is so small that the mean flow can be ignored in the first instance. Note that we will allow for the possibility that the wavenumber k₁ may have a small imaginary part allowing for decay or growth of the disturbance with x₁. Both at and downstream of the trailing edge there can be no pressure jump across the surface (the Kutta condition), and so an acoustic wave field must be added that exactly cancels the incident pressure disturbance for x₁>0, x₂=0. The scattered acoustic field p must satisfy the acoustic wave equation, and also the boundary condition that ∂p/∂x₂=0 on the surface of the plate to match the non-penetration boundary condition. If we initially limit consideration to two dimensions with no mean flow, then the scattered acoustic field is given by the solution of the Schwartzschild problem. This defines a scattered acoustic field with a harmonic pressure fluctuation $\hat{p}\left(x_1,x_2\right)exp\left(-i\omega t\right)$ that satisfies the wave equation and the boundary conditions:

$\frac{{\partial }^2\hat{p}}{\partial x_1^2}+\frac{{\partial }^2\hat{p}}{\partial x_2^2}+k^2\hat{p}=0{\left[\Delta {\hat{p}}_s\left(x_1\right)\right]}_{x_1>0}=-P_o{e}^{i{k}_1{x}_1}{\left[\frac{\partial \hat{p}\left(x_1,0\right)}{\partial x_2}\right]}_{x_1<0}=0$

Schwartzschild showed that this problem can be solved to give the pressure jump over the plate caused by the scattered wave as

$\Delta {\hat{p}}_s\left(x_1\right)=\frac{-2P_o}{\pi }{\displaystyle \underset{0}{\overset{\infty }{\int }}{\left(\frac{\left|x_1\right|}{\xi }\right)}^{1/2}\frac{e^{ik\left(\xi +\left|x_1\right|\right)+i{k}_1\xi }}{\xi +\left|x_1\right|}d\xi x_1<0}$

which on evaluation of the integral gives

$\Delta {\hat{p}}_s\left(x_1\right)=P_o{e}^{i{k}_1{x}_1}\left(\left(1-i\right)E_2\left(\left(k+k_1\right)\left|x_1\right|\right)-1\right)x_1<0$

where E₂(x) is a modified Fresnel integral defined as

$E_2\left(x\right)={\displaystyle \underset{0}{\overset{x}{\int }}\frac{e^{iq}}{{\left(2\pi q\right)}^{1/2}}dq}$

which is a function that appears often in the theory of edge scattering in several different forms.

13.2.2 Obtaining the Schwartzschild solution using the Weiner Hopf method

The result given by Eq. (13.2.2) is specific to the boundary value problem given by Eq. (13.2.1). However, we can obtain the same result in a way that may be extended to more general cases by considering the scattering in more detail. This will lead to formulations for leading edge noise and far-field radiation that do not follow directly from Eq. (13.2.2).

To obtain Eq. (13.2.2) we start by taking the wavenumber transform of the wave equation with respect to x₁, defined such that

$\widetilde{\stackrel{~}{p}}\left(\alpha ,x_2\right)=\frac{1}{2\pi }{\displaystyle \underset{-R_{\infty }}{\overset{R_{\infty }}{\int }}\hat{p}\left(x_1,x_2\right)e^{-i\alpha x_1}d{x}_1}$

(Note: since this is a wavenumber transform we have chosen the exponential to have a negative sign.) The wave equation then reduces to

$\frac{{\partial }^2\tilde{\tilde{p}}}{\partial x_2^2}+\left(k^2-{\alpha }^2\right)\tilde{p}=0$

and the solution to this equation is

$\widetilde{\stackrel{~}{p}}\left(\alpha ,x_2\right)=A\left(\alpha \right)e^{-\gamma x_2}+B\left(\alpha \right)e^{\gamma x_2}$

where

$\gamma ={\left({\alpha }^2-k^2\right)}^{1/2}$

The branch cut for γ is chosen so that Re(γ)>0. The presence of the plate implies that the wave field can be discontinuous across the plate where x₂=0, and so we can define separate solutions for the regions x₂>0 and x₂<0. The additional boundary condition that we have is that the acoustic waves must decay at large distances from the plate, and we can only meet that condition if we set B(α)=0 when x₂>0 and A(α)=0 when x₂<0. While the plate can support a pressure jump, the normal derivative of the pressure on x₂=0 must be continuous for both x₁>0 (where there is no plate) and x₁<0 (where it is zero). The pressure gradient is therefore

$\frac{\partial \tilde{\tilde{p}}\left(\alpha ,0\right)}{\partial x_2}={\left[-\gamma A\left(\alpha \right)\right]}_{x_2=0^{+}}={\left[\gamma B\left(\alpha \right)\right]}_{x_2=0^{-}}$

and so A(α)=−B(α), and the acoustic field caused by the scattered waves is given by the inverse of Eq. (13.2.4) (i.e., the inverse wavenumber transform)

$\hat{p}\left(x_1,x_2\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\mathrm{s}\mathrm{g}\mathrm{n}\left(x_2\right)A\left(\alpha \right)e^{i\alpha x_1-\gamma \left|x_2\right|}d\alpha }$

and allows for a pressure jump across the plate.

In order to solve the unknown function A(α) we use the wavenumber transform of Eq. (13.2.6) on the surface x₂=0⁺ given by

$A\left(\alpha \right)=\frac{1}{2\pi }{\displaystyle \underset{-R_{\infty }}{\overset{R_{\infty }}{\int }}\hat{p}\left(x_1,0^{+}\right)e^{-i\alpha x_1}d{x}_1}$

However, the boundary condition is different for x₁>0 and x₁<0, so we write this as

$A\left(\alpha \right)=A_{-}\left(\alpha \right)+A_{+}\left(\alpha \right)$

where

$A_{-}\left(\alpha \right)=\frac{1}{2\pi }{\displaystyle \underset{-R_{\infty }}{\overset{0}{\int }}\hat{p}\left(x_1,0^{+}\right)e^{-i\alpha x_1}d{x}_1}$

and

$A_{+}\left(\alpha \right)=\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{R_{\infty }}{\int }}\hat{p}\left(x_1,0^{+}\right)e^{-i\alpha x_1}d{x}_1}$

The integrand of Eq. (13.2.9) is known from the boundary conditions of the problem, but A₋(α) remains as an unknown. To make use of the non-penetration boundary condition we define the chordwise Fourier transform of the pressure gradient normal to the plate, given by

$C_{+}\left(\alpha \right)=\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{R_{\infty }}{\int }}\frac{\partial \hat{p}\left(x_1,0^{+}\right)}{\partial x_2}{e}^{-i\alpha x_1}d{x}_1}$

where the lower limit of the integral is zero because the pressure gradient is zero when x₁<0. However, by differentiating Eq. (13.2.6) we see that the pressure gradient is given by the inverse Fourier transform

$\frac{\partial \hat{p}\left(x_1,x_2\right)}{\partial x_2}={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left\{-\gamma A\left(\alpha \right)e^{-\gamma \left|x_2\right|}\right\}{e}^{i\alpha x}d\alpha }$

and thus C₊(α) is given by the terms in curly brackets at x₂=0⁺, which using Eq. (13.2.7) is

$C_{+}\left(\alpha \right)=-\gamma A_{-}\left(\alpha \right)-\gamma A_{+}\left(\alpha \right)$

This completely defines the boundary value problem with the conditions set by Eq. (13.2.1). The functions A₊(α) and A₋(α) are required to define the acoustic field using Eq. (13.2.6), but unfortunately only A₊(α) is known, and both A₋(α) and C₊(α) are unknowns, and so it appears that this problem is underdetermined and cannot be solved with these boundary conditions alone.

13.2.3 The radiation condition and the Weiner Hopf separation

In solving the wave equation, we used the radiation condition that requires the sound field to decay at large distances from the surface. The same condition applies far upstream or downstream from the edge, and we can use this additional boundary condition to solve for the two unknowns in Eq. (13.2.11). To ensure that waves decay as |x₁| tends to infinity we require that the surface pressure has the asymptotic values

$\underset{x_1\to \infty }{lim}\frac{\partial \hat{p}\left(x_1,0\right)}{\partial x_2}<C{e}^{-\beta x_1}\underset{x_1\to -\infty }{lim}\hat{p}\left(x_1,0\right)<D{e}^{-\beta \left|x_1\right|}$

where C, D, and β are real positive constants. (There is no need to impose a restriction on the pressure gradient for negative x₁ since the gradient is zero here anyway.) The same condition should also be required for the incident pressure disturbance, and this is achieved by requiring that Im(k₁)>β. This apparently implies that the incident wave decays from a large value upstream, but this issue can be addressed by assuming that the incident wave is of finite extent in the upstream direction, as would be the case in a real flow.

To show how this additional boundary condition can be used, we make use of some well-known properties of the Laplace transform, which is defined by the transform pairs

$F\left(s\right)=\underset{0}{\overset{\infty }{\int }}f\left(x\right)e^{-sx}dxf\left(x\right)=\frac{1}{2\pi i}\underset{-i\infty +{\beta }_o}{\overset{i\infty +{\beta }_o}{\int }}F\left(s\right)e^{sx}ds$

This transform is relevant to the problem being considered because it is essentially the same as the Fourier transform defined in Eq. (13.2.9) over the positive values of x₁, so, for example,

$A_{+}\left(\alpha \right)=F_{+}\left(i\alpha \right)/2\pi \mathrm{where}{F}_{+}\left(s\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}\hat{p}\left(x_1,0^{+}\right)e^{-s{x}_1}d{x}_1}$

Laplace transforms are used extensively in control theory and are often applied to determine if a system is stable or unstable. By definition they represent a function that is zero for x<0, and the system is stable if it does not have exponential growth as x tends to infinity. The criterion to prevent growth at infinity is that the Laplace transform of the function should have no poles, branch cuts, or other singularities on the right side of the complex s plane where Re(s)>0, as shown in Fig. 13.2.

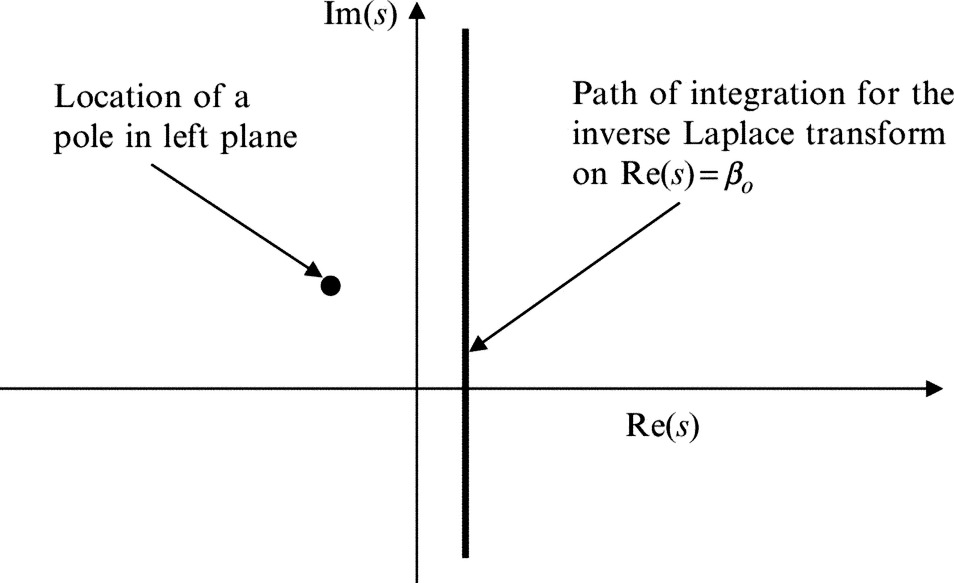
If the function f(x) decays exponentially for large x>0, so f(x)<Cexp(−βx), where C and β are positive real constants, then the Laplace transform converges when Re(s)>−β, and all the singularities of F(s) lie to the left side of the path of integration shown in Fig. 13.2. Since we wish to impose the boundary condition that the scattered field decays for large |x₁|, the criterion can be restated as requiring that all the singularities of F₊(s) lie in the region of the s plane where Re(s)<−β. We can then impose this restriction on the boundary condition given by Eq. (13.2.12) to eliminate one of the two unknown functions and obtain a complete solution.

However, before we proceed we must define the Laplace transforms of the other terms in Eq. (13.2.11). Since the pressure gradient normal to the plate is zero when x₁<0 we can define its Laplace transform as in Eq. (13.2.12), by the function G₊(s), and so C₊(α)=G₊(iα)/2π. However, for the pressure upstream of the edge, the Laplace transform must be defined by reversing the direction of integration, so (using ξ=−x₁)

$A_{-}\left(\alpha \right)=F_{-}\left(-i\alpha \right)/2\pi \mathrm{where}{F}_{-}\left(s\right)=\underset{0}{\overset{\infty }{\int }}\hat{p}\left(-\xi ,0^{+}\right)e^{-s\xi }d\xi$

So, the boundary condition may be written as

${\left[G_{+}\left(s\right)=-\gamma \left(s\right)F_{+}\left(s\right)-\gamma \left(s\right)F_{-}\left(-s\right)\right]}_{s=i\alpha }\gamma \left(s\right)={\left(-\left(s^2+k^2\right)\right)}^{1/2}$

The functions in this equation are analytic in different parts of the s plane as shown in Fig. 13.3.

It follows that the right side of Eq. (13.2.14) only converges in the strip −β<Re(s) <β. This is important when we evaluate the inverse Laplace transform defined as

$f\left(x\right)=\frac{1}{2\pi i}{\displaystyle \underset{{\beta }_o-i\infty }{\overset{{\beta }_o+i\infty }{\int }}F\left(s\right)e^{sx}ds}$

which is only valid if F(s) converges along the path of integration. The inversion of Eq. (13.2.14) is therefore required to be carried out by choosing −β<β_o<β and is only possible if β>0.

We also need to be very specific about the definition of the function γ. This is a multivalued function and, to meet the radiation condition, is required to have a positive real part. To ensure that this is the case on the path of integration Re(s)=β_o we choose the branch cuts that are shown in Fig. 13.4, and using the criteria given in Appendix B, define

$\gamma \left(s\right)=J_{+}\left(s\right)J_{-}\left(s\right)J_{+}\left(s\right)=e^{i\pi /4}{\left(s-ik\right)}^{1/2}{J}_{-}\left(s\right)=e^{i\pi /4}{\left(s+ik\right)}^{1/2}$

and require that k has a small positive imaginary part that moves the branch points away from the path of integration as shown.

All the terms in Eq. (13.2.14) are now defined along the path of integration required for the inverse Laplace transform. However, on the left side of this equation G₊(s) represents a function that is zero upstream of the edge and decays at large x₁, so it can have no singularities for Re(s)>−β. The same is therefore true for the right-hand side of this equation. This gives the additional restriction that is needed to solve Eq. (13.2.14) for the two unknowns, and we can manipulate the terms so that this criterion is met, which is the basis of the Weiner Hopf method. First divide by J₊(s) so that

${\left[\frac{G_{+}\left(s\right)}{J_{+}\left(s\right)}=-J_{-}\left(s\right)F_{+}\left(s\right)-J_{-}\left(s\right)F_{-}\left(-s\right)\right]}_{s=i\alpha }$

The first term on the right side of this equation is a mixture of functions that have nonanalytic features for both positive and negative values of real s. However, it can be split into two parts, one which exactly cancels the second term on the right (which only has singularities for Re(s)>β) and the second that has no singularities on the left side of the s plane. This separation is dependent on the form of F₊(s) which is given by the boundary condition for x₁>0 in Eq. (13.2.1) with the pressure at x₂=0⁺ being taken as half of the pressure difference Δp_s, and thus

$F_{+}\left(s\right)=-\frac{P_o}{2}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-\left(s-i{k}_1\right)x_1}d{x}_1=-\frac{P_o}{2\left(s-i{k}_1\right)}}$

This has a simple pole at s=ik₁ that is shown in Fig. 13.4. By removing the residue at the pole we can then write Eq. (13.2.15) as

${\left[\frac{G_{+}\left(s\right)}{J_{+}\left(s\right)}-P_o\frac{J_{-}\left(i{k}_1\right)}{2\left(s-i{k}_1\right)}=P_o\left(\frac{J_{-}\left(s\right)-J_{-}\left(i{k}_1\right)}{2\left(s-i{k}_1\right)}\right)-J_{-}\left(s\right)F_{-}\left(-s\right)\right]}_{s=i\alpha }$

If we take the inverse transform of this equation along the imaginary axis s=iα the right side will give a function that is zero for x₁>0 because all the terms are analytic for Re(s)<0 as shown in Fig. 13.3. Similarly, the left side will give an equation that is zero for x₁<0 (providing that J₊(s) is not zero when Re(s)>0). The only possible solution therefore is that the two sides are independently equal to zero (or equal to a function whose inverse transform is zero). We then obtain the solution for the unknown function that gives the pressure on the upstream surface as

${\left[F_{-}\left(-s\right)=P_o\left(\frac{J_{-}\left(s\right)-J_{-}\left(i{k}_1\right)}{2J_{-}\left(s\right)\left(s-i{k}_1\right)}\right)\right]}_{s=i\alpha }$

Using the definitions in Eq. (13.2.16) the pressure on the upstream part of the surface can be obtained from the inverse Laplace transform of

${\left[F_{-}\left(s\right)=\frac{P_o}{2}\left(\frac{{\left(ik+i{k}_1\right)}^{1/2}}{{\left(-s+ik\right)}^{1/2}\left(s+i{k}_1\right)}-\frac{1}{\left(s+i{k}_1\right)}\right)\right]}_{s=i\alpha }$

as a function of ξ=−x₁. Both terms in this equation have a pole at s=−ik₁ in the right half plane that individually would cause a growing wave, but since the residues of the terms cancel we can move the path of integration to the right of the pole and substitute s=s₁+ik, so the inverse transform (designated by L⁻¹{}) is

$f\left(\xi \right)=\frac{P_o{e}^{ik\xi }}{2}{L}^{-1}\left\{\frac{{\left(-i\left(k+k_1\right)\right)}^{1/2}}{\left(s_1+i\left(k+k_1\right)\right)\sqrt{s_1}}-\frac{1}{\left(s_1+i\left(k+k_1\right)\right)}\right\}$

Standard tables give the inverse Laplace transform of the functions 1/(s+a) and 1/s^1/2, which should be combined as a convolution integral when multiplied together. We then obtain the pressure jump across the surface as 2f(ξ) where

$\Delta {\hat{p}}_s\left(-x_1\right)=P_o\left(e^{-i\pi /4}{\left(k_1+k\right)}^{1/2}{\displaystyle \underset{0}{\overset{\left|x_1\right|}{\int }}\frac{e^{i\left(k_1+k\right)\tau }}{\sqrt{\pi \tau }}d\tau -1}\right)e^{i{k}_1{x}_1}{x}_1<0$

which is identical to the result given by Eq. (13.2.2).

13.2.4 Generalized Fourier transforms and Laplace transforms

The analysis given in the previous section was based on Laplace transforms to obtain the solution to the Schwartzschild problem. In much of the literature (Noble [3], Morse and Feshbach [4]) the Weiner Hopf method is carried out using Generalized Fourier transforms of the type

$F_{+}\left(\alpha \right)=\frac{1}{2\pi }{\displaystyle \underset{0}{\overset{\infty }{\int }}f\left(x\right)e^{\pm i\alpha x}dx}{F}_{-}\left(\alpha \right)=\frac{1}{2\pi }{\displaystyle \underset{-\infty }{\overset{0}{\int }}f\left(x\right)e^{\pm i\alpha x}dx}$

These are equivalent to the approach given above with ±iα replacing the Laplace transform variable s. The advantage of the current approach is that there are well-documented tables of Laplace transforms and their inverses that are readily available and can be used to simplify the results, and so this is the reason that this approach has been used here. Generalized Fourier transforms can always be obtained from Laplace transforms, providing the correct substitutions are made. However, care must be exercised in the location of branch cuts in the s plane as a function of different variables. If the wrong branch cut is chosen, then the incorrect result will be obtained.

The other benefit of the present approach is that, while different authors use different conventions for Fourier transforms, the convention for Laplace transforms is universal, and so there is little ambiguity in the final result.

13.4.1 The leading edge response

To solve the first-order problem of an upwash gust encountering a semi-infinite flat plate, as shown in Fig. 13.5, we will use the same approach as was used in Section 13.2 but with the velocity potential as the dependent variable in the wave equation rather than the pressure.

The wave equation in this case is defined by Eq. (13.3.1); the potential of the scattered acoustic field has the form $\hat{\varphi }\left(x_1,x_2,x_3\right)exp\left(-i\omega t\right)=\hat{\varphi }\left(x_1,x_2\right)exp\left(-i\omega t+i{k}_3{x}_3\right)$, and the boundary conditions are

${\left[\Delta \hat{\varphi }\left(x_1,x_3\right)\right]}_{x_1<0}=0{\left[\frac{\partial \hat{\varphi }\left(x_1,0,x_3\right)}{\partial x_2}+{\hat{a}}_2{e}^{i{k}_1{x}_1+i{k}_3{x}_3}\right]}_{x_1>0}=0$

for a harmonic upwash gust convected by the mean flow, so k₁=ω/U_∞ in this case. The solution can be obtained as before by taking the wavenumber transform of the wave equation. The final result will be of the same form as Eq. (13.3.5) with the velocity potential replacing the unsteady pressure and the requirement that the gradient of the velocity potential is continuous across the plate. The boundary conditions can then be defined using the half-range transforms given by Eqs. (13.2.7) through (13.2.10), with the subscripts referring to the upstream or downstream part of the x₁ axis, so

$C_{-}\left(\alpha \right)+C_{+}\left(\alpha \right)=-\gamma A_{-}\left(\alpha \right)-\gamma A_{+}\left(\alpha \right)$

In this case A₋(α)=0 and

$C_{+}\left(\alpha \right)=\frac{-{\hat{a}}_2}{2\pi i\left(\alpha -k_1\right)}$

As before this equation has two unknowns A₊(α) and C₋(α), so we need to use the radiation condition as |x₁| tends to infinity to find a solution. The procedure used in Section 13.2 is followed again by writing the boundary condition in terms of the Laplace transforms defined in Eq. (13.2.14) with the velocity potential as the dependent variable and s=iα, so

${\left[\frac{-{\hat{a}}_2}{\left(s-i{k}_1\right)}+G_{-}\left(-s\right)=-\gamma \left(s\right)F_{+}\left(s\right)\right]}_{s=i\alpha }$

We need to separate the terms in this equation that contribute to the wave field upstream or downstream of the leading edge, and this is achieved by factorizing γ(s), as in Eq. (13.3.6) identifying those terms that have singularities in the right or left side of the s plane. From Fig. 13.4 we see that the factored equation takes the form

${\left[\frac{-{\hat{a}}_2}{\left(s-i{k}_1\right)J_{-}\left(s\right)}-\frac{-{\hat{a}}_2}{\left(s-i{k}_1\right)J_{-}\left(i{k}_1\right)}+\frac{G_{-}\left(-s\right)}{J_{-}\left(s\right)}=-J_{+}\left(s\right)F_{+}\left(s\right)-\frac{-{\hat{a}}_2}{\left(s-i{k}_1\right)J_{-}\left(i{k}_1\right)}\right]}_{s=i\alpha }$

As before the inverse Laplace transform of the left side of this equation gives a function that is zero for x₁>0, while the right side gives a function that is zero for x₁<0 providing that the imaginary part of k₁ is greater than zero. We then obtain the Laplace transform of the jump in potential across the surface downstream of the leading edge as

$F_{+}\left(s\right)=\frac{{\hat{a}}_2}{\left(s-i{k}_1\right)J_{-}\left(i{k}_1\right)J_{+}\left(s\right)}$

or, in terms of the wavenumber spectrum of the potential jump,

$A\left(\alpha \right)=A_{+}\left(\alpha \right)=\frac{{\hat{a}}_2}{2\pi i\left(\alpha -k_1\right)J_{-}\left(i{k}_1\right)J_{+}\left(i\alpha \right)}$

The inverse Laplace transform of Eq. (13.4.2) gives the potential jump, but in this case it is useful to evaluate the unsteady pressure jump

$\Delta {\hat{p}}^{\left(1\right)}\left(x_1,x_3\right)e^{-i\omega t}=-{\rho }_o\frac{D_{\infty }}{Dt}\left(\Delta \hat{\varphi }\left(x_1,x_3\right)e^{-i\omega t}\right)$

and since (ω−αU_∞)=(k₁−α)U_∞ and the pressure jump is the inverse transform of 2A(α), we obtain

$\Delta {\hat{p}}^{\left(1\right)}\left(x_1,x_3\right)=\frac{-{\rho }_o{U}_{\infty }{\hat{a}}_2{e}^{i{k}_3{x}_3}}{\pi \beta {\left(k_1+k_{o}M+\kappa \right)}^{1/2}}\underset{-\infty }{\overset{\infty }{\int }}\frac{e^{i\alpha x_1}}{{\left(\alpha +k_{o}M-\kappa \right)}^{1/2}}d\alpha$

The inverse transform can be evaluated from tables, and we find that

$\begin{array}{c}\hfill \Delta {\hat{p}}^{\left(1\right)}\left(x_1,x_3\right)=\pi {\rho }_o{\hat{a}}_2{U}_{\infty }{g}^{\left(1\right)}\left(x_1,k_3,\omega ,M\right)e^{i{k}_3{x}_3}\hfill \\ \hfill g^{\left(1\right)}\left(x_1,k_3,\omega ,M\right)=\frac{-2e^{i\left(\kappa -M{k}_o\right)x_1+i\pi /4}}{\pi {\left(k_1+\kappa {\beta }^2\right)}^{1/2}\sqrt{\pi x_1}}{x}_1>0\hfill \end{array}$

(where we have used β²(k₁+k_oM)=k₁). The important conclusion from this result is that the pressure jump at the sharp edge has a square root singularity and tends to zero at large distances downstream of the leading edge. The implication is that both the pressure jump and the particle velocity at the leading edge are infinite, but in reality the velocity at the edge will be limited by viscous effects and the details of the geometry. The modeling that has been used here is based on thin airfoil theory, which ignores that rounding of the leading edge of a blade. When the details of the rounding are included in the analysis the leading edge pressure jump will be quite different as discussed in Chapter 7 for incompressible flow.

13.4.2 The trailing edge correction

For a blade with a finite chord these results need to be corrected for the effect of the trailing edge and the Kutta condition. We can calculate a correction that satisfies the trailing edge boundary condition by using the trailing edge scattering theory described in Section 13.2. However, this result is for a semi-infinite flat plate, and so there will be a residual error that occurs at the blade leading edge. Successive corrections can be calculated using the methods described here, but first we will consider the first-order trailing edge correction that is obtained by solving the trailing edge boundary value problem described with the incident pressure jump given by Eq. (13.4.5). Since the origin in the leading edge problem is at a distance c upstream of the trailing edge the result given by Eq. (13.4.5) must be redefined with the origin at the trailing edge, giving

$\Delta {\hat{p}}^{\left(1\right)}\left(x_1,x_3\right)=\pi {\rho }_o{\hat{a}}_2{U}_{\infty }\left\{\frac{-2e^{i\left(\kappa -M{k}_o\right)\left(x_1+c\right)+i\pi /4}}{\pi {\left(k_1+\kappa {\beta }^2\right)}^{1/2}\sqrt{\pi \left(x_1+c\right)}}\right\}{e}^{i{k}_3{x}_3}$

Carrying out the full Weiner Hopf procedure on this function is difficult, but a simplified result is obtained in the high-frequency limit if the amplitude variation with x₁ is ignored, and we approximate the pressure near the trailing edge as

$\Delta \hat{p}\left(x_1,x_3\right)\approx \pi {\rho }_o{\hat{a}}_2{U}_{\infty }\left\{\frac{-2e^{i\left(\kappa -M{k}_o\right)c+i\pi /4}}{\pi {\left(k_1+\kappa {\beta }^2\right)}^{1/2}\sqrt{\pi c}}\right\}{e}^{i\left(\kappa -M{k}_o\right)x_1+i{k}_3{x}_3}$

We can then use the analysis given in Section 13.2 to find the trailing edge correction as the additional pressure jump

$\begin{array}{l}\Delta {\hat{p}}^{\left(2\right)}\left(x_1,x_3\right)=\frac{-2\pi {\rho }_o{\hat{a}}_2{U}_{\infty }{e}^{i\left(\kappa -M{k}_o\right)\left(x_1+c\right)+i\pi /4}}{\pi {\left(k_1+\kappa {\beta }^2\right)}^{1/2}\sqrt{\pi c}}\left\{\left(1-i\right)E_2\left(2\kappa \left|x_1\right|\right)-1\right\}{e}^{i{k}_3{x}_3}\\ x_1<0\end{array}$

If the origin of the coordinate system is relocated back to the leading edge, we obtain the corrected nondimensional surface pressure function as

$g^{\left(1+2\right)}\left(x_1,k_3,\omega ,M\right)=\frac{-2e^{i\left(\kappa -M{k}_o\right)x_1+i\pi /4}}{\pi {\left(k_1+\kappa {\beta }^2\right)}^{1/2}\sqrt{\pi c}}\left\{\sqrt{\frac{c}{x_1}}+\left(1-i\right)E_2\left(2\kappa |x_1-c|\right)-1\right\}0<x_1<c$

The corrected solution given by Eq. (13.4.6) is only an approximate solution, but includes the major effects caused by the trailing edge, and ensures that the Kutta condition is satisfied. The pressure jump includes a discontinuity upstream of the leading edge because we have used a trailing edge correction that assumes it is the same as the response of a semi-infinite flat plate upstream of the trailing edge. However, for large arguments we find that

$\left(1-i\right)E_2\left(2\kappa c\right)\approx 1+O\left({\left(2\kappa c\right)}^{-1/2}\right)$

so this correction is small when the blade chord is large compared to the acoustic wavelength.

In conclusion we have developed expressions for the response of a flat plate airfoil to a harmonic gust and obtained the unsteady surface pressure distribution, which can be used to calculate the unsteady loading and the far-field sound. These results are crucial to the calculation of sound radiation from thin airfoils and, although the derivation is complex, the results are important to our understanding of the problem. We will discuss the features and characteristics of the results in the following chapters.