Chapter 10. Compressional Structures: Balancing and Interpretation*
* For all figures in this chapter (in the printed book only), see the preface for information about registering your copy on the InformIT site for access to the electronic versions in color.
Introduction
The first edition of ASGM contained one chapter on structural geological methods. Since knowledge of structural geology plays a key role in interpretation and mapping, as discussed in number 2 of the Philosophical Doctrine, we believed the chapter was important to the overall content of the textbook. Because of advances in structural geology and balancing during the following decades, in this third edition we have expanded the one chapter into four separate chapters covering compressional, extensional, strike-slip, and growth structures. Knowledge of structural methods in these various tectonic settings will improve your ability to generate viable, valid 3D interpretations, maps, and prospects as well as improve your ability to develop field discoveries. In addition, a number of significant structural advancements occurred since the publication of the second edition, and we have added new sections to the compressional and extensional chapters.
In the age of computer-generated work products, geoscience companies have developed a variety of software programs that can balance most of the common geological structures. It is not our intent to review or discuss these software programs and their various capabilities. Rather, our intent is to implant on the interpreter of geological and seismic data an understanding of the geometric processes that form the basic structural styles. This approach has value, as the interpreter benefits from a knowledge of the geological processes that are inherent to the algorithms that form the basis of the software, thus removing the black-box aspect of these programs. The approach should result in better interpretations of the data.
We begin the structural geology section of the third edition with a review of compressional techniques and methods. Much of modern structural geological analysis began with the study of compressional tectonics, and therefore it is appropriate to start here. These four structural chapters center around specific structural methods and techniques. A basic understanding of rock mechanics and structural geology, presented in such textbooks as Billings (1972); Suppe (1985); Woodward, Boyer, and Suppe (1985); and Marshak and Mitra (1988), is a prerequisite to understanding and applying the techniques presented in this chapter.
Structural Geology and Balancing
Compressional structures contain extensive proven petroleum reserves in many areas of the world. But even more accumulations remain undiscovered, and existing fields are insufficiently exploited, because the typical complexity of compressional structures and inadequate seismic images inhibit reasonable and accurate interpretation and mapping. Critical to the best possible analysis of the data is the interpreter’s knowledge of compressional structural geology and the application of techniques that lead to geologically reasonable interpretations and accurate maps.
One of the most important of the compressional structural geological techniques is structural balancing. The ultimate goals of balancing are to restore complexly deformed rock to its initial state or to its correct palinspastic restoration and to determine the geological sequence of events. Such information can be very useful to the geologist or geophysicist. Not only is the geometry of the structure better understood, resulting in better and more accurate prospect and reservoir maps, but geological trends such as sand patterns can be more accurately located. An understanding of the timing of the structural events should aid in oil migration studies and define how and where fluids may have entered the structure. If the geometry of the structure is understood, then this knowledge can be used to more accurately process seismic data, which in turn results in an even better understanding of the geometries. Balancing can also be effectively used to check assumptions and interpretations (Tearpock et al. 1994). Lastly, balancing tends to keep the interpreter more focused. If the section does not balance, then perhaps it is time to reconsider the interpretation. Why drill a well to determine that the interpretation does not balance when restoration can determine a misinterpretation prior to the drilling? Our experience with balancing, as well as that of our colleagues, indicates that balanced, geologically possible interpretations can discover significant additional reserves. In short, balancing works.
Structural balancing is based on the intuitively satisfying concept that the interpreter must neither create nor destroy volume during the interpretation process (Goguel 1962). Interpreters may inadvertently introduce a volume imbalance anytime a fault is mis-picked or a horizon is miscorrelated. Fortunately, balancing can detect volume problems prior to the drill bit. Thus, it follows that an interpreted map or cross section, whether it be a geological or seismic section, should volumetrically restore without overlaps or voids in the stratigraphic section. Faulted and folded beds should be restorable to their initial subhorizontal state (Tearpock et al. 1994). Thereby, a structural interpretation may be tested for admissibility. An analogy might be a child who removes a new block puzzle from a box and places it on the floor. Once all the pieces of the puzzle have been removed from its container, the puzzle can be restored to its initial state by placing each block back into its proper position. The first attempt by the child at restoring the puzzle may result in most of the pieces being placed into the box, with one or two pieces remaining on the floor. A second attempt could result in all of the pieces being placed in the box, but with some of the pieces being tilted at various angles or forced to fit.
The geoscientist experiences similar problems when attempting to retrodeform (restore) geological and/or geophysical data. Of course, the correct solution to a puzzle is one that has been perfectly restored to its initial position. There are two types of interpretations: interpretations that are admissible, or geologically possible, and interpretations that are inadmissible, or not geologically possible (Elliot 1983). A balanced interpretation is an admissible interpretation in which the horizons can be restored to their initial subhorizontal position by unfolding the horizons and rotating the beds back to a subhorizontal position along the interpreted faults.
The benefits of balancing are fundamental to correct geological interpretations. The earth’s subsurface contains no voids or mass overlaps; thus, a section that does not balance cannot be geologically reasonable on simple geometric grounds. Unfortunately, a balanced section, although physically reasonable, need not necessarily result in the correct geological interpretation. Balancing is not unique, and two geoscientists can produce two balanced sections that are not alike. Obviously, the more complete the data set and the better the interpretive techniques, the more likely that the balanced section will reflect reality.
Balancing is still a developing science, and new techniques and interpretations are progressively being introduced. Nevertheless, an interpretation tempered by a concept of mass conservation is the key to admissible geological interpretations and constructions. If the structural interpretation is correct, then balancing techniques can be used to quantify the interpretation.
Balancing can be subdivided into two disciplines: classical balancing, which was primarily developed by Goguel (1962), Bally et al. (1966), and Dahlstrom (1969) and his coworkers; and nonclassical balancing, which was primarily developed by Suppe (1983, 1985) and his students and coworkers. Most of the concepts presented in this introduction can be attributed to Goguel and Dahlstrom.
Mechanical Stratigraphy
For many years, structural geologists have argued about the mechanical properties of the upper crust. Does it exhibit elastic and/or frictional behavior as indicated by earthquakes, or is it viscoelastic or viscoplastic, as indicated by the bent strata in the hinge zone of folds? Could time be a factor? Do the sedimentary strata buckle out (Biot 1961), or do the strata follow faults within the sedimentary section (Rich 1934)? Although all of these mechanisms are possible, the evidence now strongly suggests that the deformation that occurs in petroleum basins is primarily controlled by brittle (low temperature) deformation processes, and that the viscous deformation expressed by fold trains (Fig. 10-1) is confined to metamorphic belts (Tearpock and Bischke 1980). The fold style depicted in Figure 10-1, with its near constant wavelength, is not commonly observed in petroleum basins, and thus another deformation mechanism is required to explain the folds that trap hydrocarbons. This mechanism appears to be frictional deformation. Davis et al. (1983), Dahlen et al. (1984), and Dahlen and Suppe (1988) formulate a frictional, or brittle, theory of crystal deformation that applies to both compressional and extensional regimes. The theory resolves the overthrust paradox (Smoluchowski 1909; Hubbert and Rubey 1959) and is consistent with the geological and seismic information collected from petroleum basins. Our intention here is to apply this theory and its observations to our areas of interest. Readers who maintain an interest in mechanics can consult the references listed at the end of this textbook.

Figure 10-1 Example of a fold train commonly observed in metamorphic belts.
The frictional theory of crystal deformation states that when folds form, the maximum principal stress (σ1) is inclined slightly to the bedding surfaces (Fig. 10-2). The rock will then fracture along angles that are dependent on the pore pressure and the intrinsic strength of the rock. The weaker the rock, the lower the angle between σ1 and the fracture.
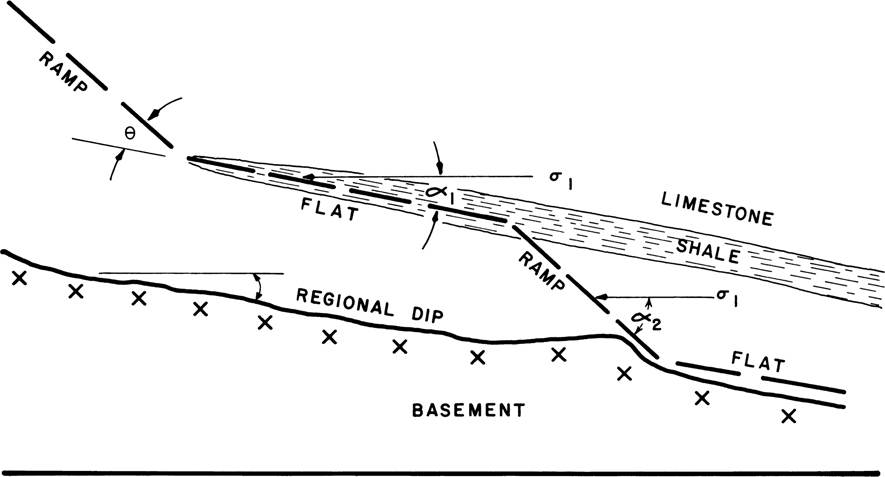
Figure 10-2 Cross section of ramp geometry. For explanation, see text. (Modified after Rich 1934; AAPG©19341934, reprinted by permission of the American Association of Petroleum Geologists (AAPG) whose permission is required for further use.)
For example, consider an alternating sequence of limestone and shale layers (Fig. 10-2). Intuitively, shale layers seem to be weaker than better consolidated limestone layers, and it is well known that shales can contain abnormally high fluid pressures that drastically weaken these rocks. The theory states that because shales are weaker than limestone, the angle (α1) between σ1 and the fractures in shales must be smaller than the angle (α2) between σ1 and the fractures in limestones (Fig. 10-2). As σ1 is slightly inclined to the bedding, the fractures in the shales are more subhorizontal than the fractures in the limestones. This leads to the primary conclusion of this section: in more competent or stronger rocks, the fractures will form at a high angle to bedding, and in the incompetent rocks, such as overpressured shales, the fractures tend to form parallel or subparallel to bedding.
If motion along these fractures causes them to coalesce, then a decollement, or zone of detachment, will form along the flat-lying bedding and may follow incompetent (shale or evaporite) horizons for tens or even hundreds of kilometers (Davis and Engelder 1985). In areas where the weaker layers gain strength or are pinched or faulted out, the decollement may ramp to a higher structural level (Fig. 10-2). As these ramps must pass through rocks that are stronger and have lower pore pressures than shales, the angle (α2) between σ1 and the fractures will be larger. Thus, ramps have higher angles with respect to the bedding than do the flatter portions of thrust faults (Fig. 10-2).
Where the ramp connects to a weaker layer on a higher structural level, the ramp transforms into a flat once again. Once a network of ramps and flats forms and a large force is applied to the back of the wedge-shaped region in Figure 10-2, the strata above the flats and ramps will begin to move along the fault. Material will begin to slide along the flats and up the ramps, forming a fold in the hanging wall block. Eventually, large folds will form in a manner that was initially described by Rich (1934), but this process is the subject of a later section.
The angle at which the ramp steps up from the bedding is called the cutoff, or step-up, angle (θ in Fig. 10-2). This angle is often characteristic of, or fundamental to, a particular fold-thrust belt and depends on both the pore pressure in the rock and the rock type. Similar relationships may exist in extensional terrains. The characteristic cutoff angle in certain fold-thrust belts is generally less than 20 deg and tends to vary within several degrees of its mean value. For example, in Taiwan the characteristic step-up angle is 13.3 deg ± 2.4 deg (Suppe and Namson 1979; Dahlen et al. 1984). An attempt must be made to determine this angle prior to a balancing study. This step-up angle will be used to balance your structures. Note that the step-up angle is measured relative to regional dip rather than to the horizontal.
There appear to be at least three methods that give insight into estimating the characteristic step-up angle. Field studies or a literature search can be conducted in the area of interest. As the step-up angle is the angle between the flat and the ramp, field measurements or a description of this relationship will provide the required answer. A second, less direct measurement technique is to observe a well-imaged ramp and flat on a seismic section that is perpendicular to the strike of the fault surface. The section must first be depth-converted to make this measurement. The strata above the ramp will parallel the ramp, and thereby the step-up angle can be determined relative to regional dip (Fig. 10-34). Therefore, a study of the dips across an area may give insight into the characteristic step-up angle. For this method, it is first necessary to know the regional or undeformed dip of the area. For example, suppose that an area has no regional dip. It therefore follows that the nontilted beds will have zero dip. Strata that have moved up ramps, and are deformed, may dip at 12 deg. The characteristic step-up angle is therefore 12 deg. We might, however, be faced with a situation in which 20% of the dips are near zero, 30% are 3 deg, and 50% are about 9 deg or greater. The problem here is attempting to decide whether the regional dip is zero or 3 deg and whether the step-up angle is 9 deg or 12 deg or greater. This matter is often resolved by finding that one of these choices simply works better than the other during the restoration, or balancing, process.
Classical Balancing Techniques
In previous sections we introduced the concepts of volume conservation and brittle deformation, which we apply to petroleum basins and not to metamorphic belts, which often lie adjacent to our areas of interest. Here we develop these concepts in a manner that can lead to the interpretation and mapping of structures that better define prospects.
The volume conservation concepts that are developed in this section, although rigorous in their general application, do not precisely specify how this volume is to be conserved. Thus, a significant degree of artistic license is left to the interpreter. For this reason, the classical techniques developed by Goguel (1962) and Dahlstrom (1969) are ultimately qualitative in their approach. No formula or graph constrains the interpretation.
Volume Accountability Rule
The basic principle behind all balancing techniques is that nature, and not the interpreter, can create or destroy rock units, and that the interpreter should account for all of the present or pre-existing volume. Engineers are familiar with this concept as one of mass or volume balance, or of volume accountability. Most geoscientists are quick to point out that geological compaction, particularly in growth structures, changes volume with time. In addition, fluid flow through limestone can remove volume by pressure solution, and this volume reduction can be significant (Groshong 1975; Engelder and Engelder 1977). Arguments of this type, although correct, should not be substituted for lazy thinking. We have discovered that even thinking about growth structures in terms of strict volume conservation has forced the development of new balancing and interpretation techniques. If the structure does not balance volumetrically, then what process is causing the imbalance? The conservation of volume principle at least brackets the error or helps define the amount of volume reduction due to compaction or pressure solution. In the case of widespread volume removal, regional balancing and structural analysis may indicate that another process is occurring and to what extent. We normally find, however, that these volume reduction processes are not a major concern and that the interpreter normally can think in terms of volume conservation while being prepared for alternatives.
The economic issue that needs to be addressed here is much more practical and much more likely to confront the interpreter on a daily basis than is pressure solution. Interpreters often unknowingly have a tendency to introduce mass overlaps and gaps into their interpretations (Tearpock et al. 1994). Often, these gaps or overlaps are confined to a particular region of their cross sections or to a particular structure. For example, a given seismic-based cross section and prospect, upon retrodeformation, has twice as much volume between sp (shotpoint) 320 and sp 420 (at about 1.5 sec to 2.2 sec) and no volume between sp 285 and sp 400 (at about 2.8 sec to 3.1 sec). An obvious question thus arises: Does this volume incompatibility affect the viability of the prospect, and would a better interpretation enhance or detract from the prospectivity of the area? Therefore, balancing literally attempts to take the “holes” out of our interpretations, as is shown in the Retrodeformation section in this chapter.
Area Accountability
In the Mechanical Stratigraphy section, we describe the petroleum basin as a low-temperature regime subject to brittle (i.e., frictional) deformation. In such an environment, flow, elongation, and flattening are not of primary importance, and thus the 3D volume problem can be reduced to 2D. In other words, we shall assume that material is not entering or leaving the plane of the geological cross section, and therefore the problem can be reduced to 2D (Goguel 1962). Notable exceptions to this rule would be shale and salt diapirs, which are typically 3D phenomena. These salt structures, which are associated with withdrawal and rim synclines surrounding the diapir (Trusheim 1960), contain a wealth of information that defines salt flowage and can be used to balance salt diapirs in 3D. Another exception is the bifurcating normal fault structure, which moves material out of the plane of cross section. Techniques for studying this type of deformation are briefly addressed in Chapter 11. In the meantime, however, and as long as the deformation is brittle and the transport direction is subperpendicular to fault strike, the 3D problem can be reduced to a 2D cross section that is subperpendicular to the strike of the fault.
Bed Length Consistency
If we accept the premise that petroleum-bearing rocks are brittle and deform at temperatures within the hydrocarbons window, then the 2D problem can be linearized (Goguel 1962). In other words, if there is no large-scale material flow within or across the plane of the 2D cross section, then the seismic reflection or bed length before deformation will remain the same after deformation (Fig. 10-3). This logic will also hold true for the thickness of each bed involved in the deformation, which means that the folding will be of the parallel type. Thus, bed length can be utilized to balance cross sections. If a sedimentary sequence is 2 km long before deformation, it must remain 2 km long after the deformation. The bed may be bent and it may be broken, but it should still be 2 km long.

Figure 10-3 Deformation map of petroleum basins versus metamorphic belts. Low temperatures tend to preserve cross-sectional volume, whereas in metamorphic belts, material will flow in and out of the plane of cross section.
Although the logic inherent in the above statement may seem self-evident, it appears to be one of the primary causes of the so-called balanced cross section, which is prevalent throughout the literature. The above logic implies that if one measures the bed lengths across a cross section, and the bed lengths are equal on all levels, then the cross section will balance. In practice, however, small changes in the lengths of lines can result in significant volume changes that result from inaccuracies in, or a lack of, subsurface dip data. This follows from the trigonometric relationship that at low angles the length of the adjacent line is about equal to the hypotenuse (Fig. 10-4). Consequently, we can see that the line segment AB is about equal to AC, even though the thickness AX is not equal to the thickness CZ. Therefore, we can often check existing cross sections by simply observing whether beds or formations are subject to unexplained or nonuniform thickness variations. If these thickness variations are not due to logical variations in stratigraphic thickness, then the interpretation should be subjected to further analysis.
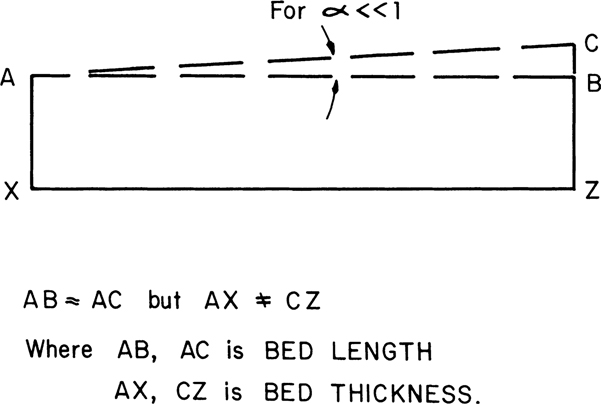
Figure 10-4 Noticeable changes in bed thickness result in small changes in bed length.
Pin Lines
A significant development was made by Dahlstrom (1969), who realized that you can check the validity of any cross section by measuring bed lengths, while keeping an eye out for variations in the thickness of units. This is accomplished through the use of pin lines (Dahlstrom 1969). In this procedure, one attempts to locate regions that are not subject to deformation (such as shear or bedding plane slip) and then affix these regions to the basement by driving an imaginary pin vertically through the cross section. Pins are used as a basis for measurement, and bed length consistency is then measured relative to these pin lines (Fig. 10-5). Dahlstrom realized that bed length consistency must be preserved on all structural levels in both 2D and 3D, and that if the bed length consistency does not hold from one section to another, then the interpretation is likely to be in error. Figure 10-5 is modified from Dahlstrom (1969) with Figure 10-5a signifying the undeformed pin state. If the unit is concentrically folded and displaced a distance S, then the bed length (lo) within the concentric fold after deformation should be the same length (lo) as it was before deformation (Fig. 10-5a and b).

Figure 10-5 Pin lines and bed length consistency. (a) Undeformed bed state. (b) Bed length differs from pin length. (c) Deformed bed. (Modified after Dahlstrom 1969. Published by permission of the National Research Council of Canada.)
In Figure 10-5b, the bed length (lo) within the folded unit is not the same as the pin length (l). This follows, as the folded unit has been shortened a distance S (compare Fig. 10-5b and c). In Figure 10-5c, dipping beds overlie flat beds, which is the classic indication of a geometric discontinuity or decollement (thrust fault). We call this method for picking thrust faults Dahlstrom’s rule, and the thrust fault exists between the steeper dipping and the flatter dipping beds (Fig. 10-5c). Thus, when picking thrust faults on seismic data, simply look for steeply dipping beds over more gently dipping beds. These steeply dipping beds must be structurally deformed and typically are inclined at more than 5 deg to regional dip.
Line-Length Exercise
Line-length balancing can be a powerful quick-look tool (Tearpock et al. 1994). We present an example of how line-length balancing may find additional oil in producing fields. Figure 10-6a represents two dip profiles that are similar to those in a large producing trend in South America. The two profiles are from the same field, traverse the same anticlinal structure, and are a short distance from each other. Good to fair quality seismic data from the field image the top of the structure but do not clearly image Faults A, B, and C. Well No. M-5 on profile A and other wells in the field cut Fault A, but Fault B is inferred from the relatively dense well control (Fig. 10-6a). Notice that Wells No. M-1 and M-3, which penetrate the front of the structure on profiles A and B, encounter the reservoir section at a greater depth than do the structurally higher Wells No. M-2 and M-4. Seismic data from an adjoining field on the same structure are of good to excellent quality and clearly image Fault C, which is a bedding plane thrust. Fault C was mapped into the area of profiles A and B from the adjoining field.
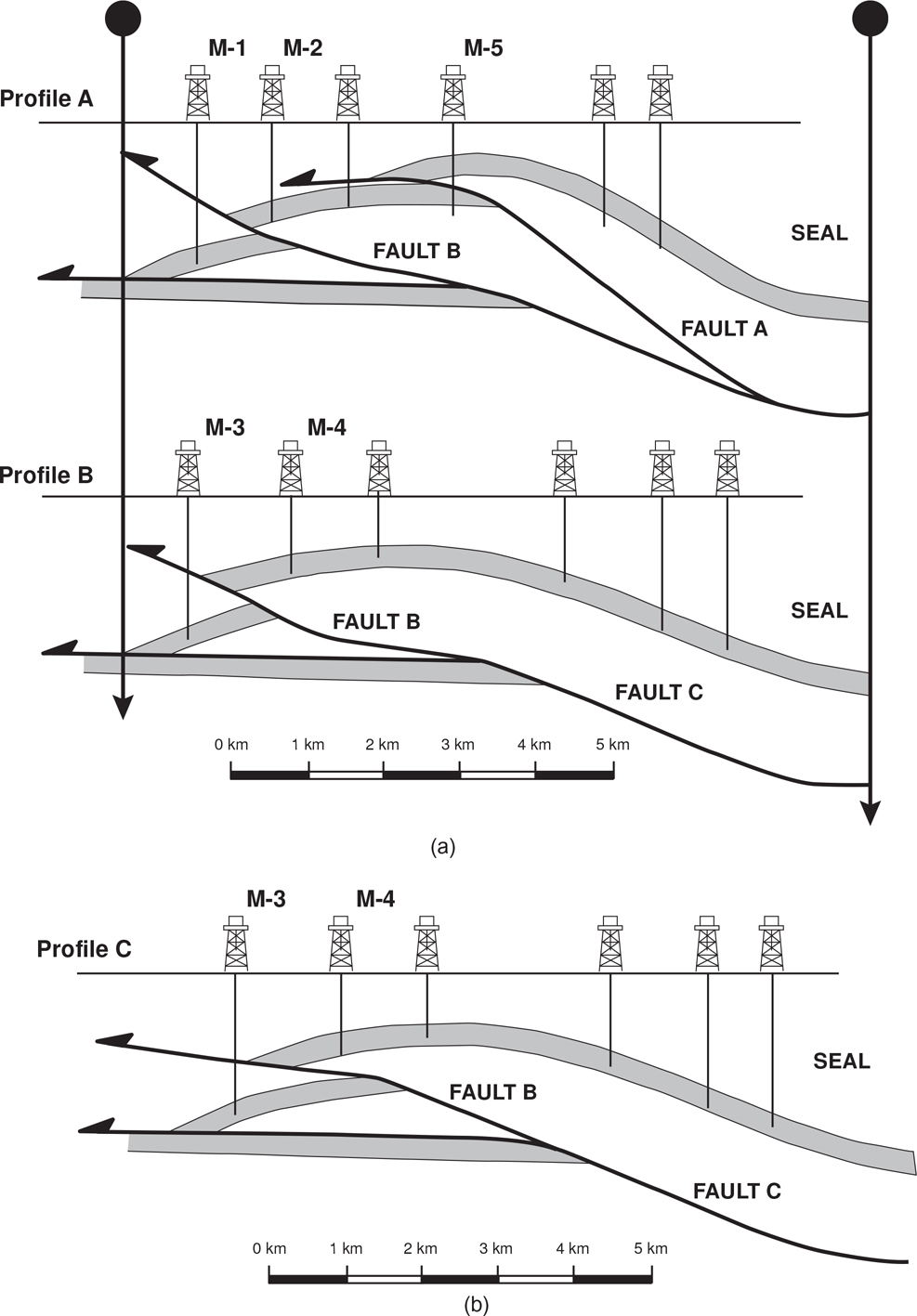
Figure 10-6 (a) Profiles A and B constructed across an anticline that forms a producing field. The slip imbalance between the two profiles creates a line-length imbalance, as described in text. (b) Profile C represents a reinterpretation of profile B using line-length balancing concepts. Profile C, which uses a ramp-flat thrust fault geometry common to fold-thrust belts, introduces additional potential in the reservoir in the lowermost imbricate block. (Published by permission of R. Bischke.)
The interpretation shown on profile A contains three imbricate blocks formed by Faults A, B, and C. Faults A and B link to large Fault C. The footwall reservoir section has the same bed length along profiles A and B, so pin the structure at the hanging wall cutoff position located in the structurally lowest imbricate blocks (left-hand pin). The pin on the right penetrates the syncline in an off-structural position. In the hanging wall portions of the fold, use a balancing program or a ruler to measure the bed lengths of the reservoir bed along its top. The beds are cut by the faults, so the top of the bed in each imbricate block terminates at the faults. Therefore, do not include as bed length the distance along a fault. On profile A, the hanging wall bed lengths in the three imbricates are about 11.8 km total.
Repeating the bed length measurements on profile B, located a short distance from profile A, results in a hanging wall bed length, at the top of the reservoir horizon, of about 10.8 km. Thus, between the two profiles there is a line-length imbalance along the top of the reservoir bed, and profile A contains 1 km more bed length than profile B. Perhaps the faults are dying out, but the profiles are near the center of the trend, which is over 100 km long. Over short distances, the slip along faults is not likely to change significantly along strike (Dahlstrom 1969; Elliot 1976; see bow-and-arrow rule in the Cross-Section Consistency section of this chapter). How may we reconcile this line-length imbalance between the two profiles, and what are the implications?
Notice on profile A that the reservoir horizon is repeated in Well No. M-5. Abundant well log data from the field demonstrates that Fault A dies out before reaching profile B. In fold-thrust belts and over short distances, the slip along thrust faults is about constant along strike (see Cross-Section Consistency). Thus, it is unlikely that Faults A and B would both grow smaller over such a short distance. Alternatively, slip transfer between faults is common in fold and thrust belts (Dahlstrom 1969) (Fig. 10-14). The slip on Fault A may transfer to Fault B. In other words, as Fault A dies out, the slip on Fault B increases at the expense of fault A.
What are the consequences of a 1 km slip transfer between the two fault surfaces, and how could this slip transfer affect reserves? If Fault B is larger than shown in profile B, then Fault B may overthrust a larger portion of the lower imbricate block penetrated by Well No. M-3. We proceed to line-length balance the data and present an alternative interpretation of the data shown in profile C in Figure 10-6b. Profile C contains an additional 1 km of bed length relative to profile B, so that the bed lengths on profiles A and C are both about 11.8 km. The interpretation shown on profile C uses the concept of a ramp-flat fold geometry that is common to fold-thrust belts (Bally et al. 1966), rather than the upward-listric reverse fault shown on profiles A and B. Upward-listric fault surfaces are common to extensional terranes (Chapter 11). As line-length balancing concepts suggest that the bed length should be about 11.8 km on the two profiles, and as we must honor the existing well control, we consider the solution shown in profile C. Profile C contains an additional 1 km of slip on imbricate Fault B. This increase in slip creates more repeated section in the lowermost imbricate block beneath Well No. M-4. This interpretation of the data is exciting, as the new interpretation extends the reservoir horizon in the lower block between Faults B and C by about 1 km to the right, introducing upside potential. This potential exists up-dip of the producing Well No. M-3. The solution shown in profile C may require a reinterpretation of profile A. This example shows how line-length balancing may find new oil in old fields.
Balancing sections using the structural workstation (see the following section, Computer-Aided Structural Modeling and Balancing) is an alternative to manual line-length balancing procedures. Profile D in Figure 10-7, generated on a structural workstation, uses area-balancing concepts. Profile D maintains not only line-length balance but also cross-sectional area balance (see the section Retrodeformation in this chapter). Therefore, profile D in Figure 10-7 is more geometrically accurate than profile C in Figure 10-6b. However, the two profiles are similar.

Figure 10-7 Profile D is a reinterpretation of profile C in Figure 10-6b, using structural workstation methods based on balancing concepts. Profile D is similar to the line-length balanced profile C. (Published by permission of R. Bischke.)
Computer-Aided Structural Modeling and Balancing
Structural analysis, interpretation, and modeling rely heavily on the graphical representation of structural horizon and fault surface geometry. Using structural workstation software, the end product of this graphical representation results in the construction of cross sections. Graphical methods of structural analysis can be applied to geological data to determine the viability of cross sections. Historically, structural modeling relied heavily on manual drafting to create cross sections. The emergence and enhancement of computer workstations during the 1990s provided a powerful tool for 2D and 3D structural evaluation. The workstation facilitates the visualization and modeling of structural data and allows interpreters to attack more complicated structural problems (Fig. 10-8). Utilizing workstation software, it is possible to move quickly from the time domain of seismic data into the depth domain of structural visualization. Depth visualization by geoscientists enables the creation of a more complete and accurate depiction of the subsurface structural geology. The technical and economic benefits of computer-aided structural analysis are important, if not key, to the success of petroleum exploration and production in structurally complex areas.
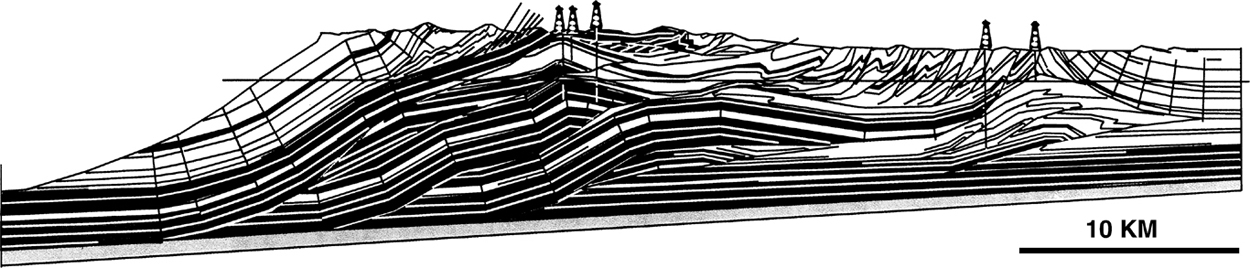
Figure 10-8 Structural cross section across Savanna Creek Duplex and Canadian Rockies. (Published by permission of D. Roeder 1983.)
After reviewing the different structural styles presented in Chapters 10 through 12 and their associated algorithms, one may ask, “What is the best and most effective method of applying structural information?” One important approach is the proper use of structural workstation software.
Seismic data are the primary subsurface information; therefore, it is critical to translate seismic time models into seismic depth models. Once depth intervals are selected and assigned respective velocities, the structural workstation software should provide a means to readily move between the time sections and the related depth domains. Data quality and knowledge of related acoustic interval velocities determines the accuracy of the time-depth transition. Again, the workstation is an excellent tool for testing different time-depth pairs. Iteration of structural models utilizing an array of alternative concepts helps to refine and perfect the interpretation, which is another strong justification for the implementation of computer-aided structural analysis.
Animated models of fault bend folds, fault propagation folds, and so on, are possible on the workstation. These animated models are helpful when visualizing and constructing forward models of simple structures and illustrating the origin of structures. The identification and accurate depiction of fault surfaces from seismic data sets is one of the most important steps of seismic structural interpretation. There is a direct relationship between the geometry of the fault surfaces and the geometry of structure horizons related to the fault surfaces. The relationship between fold shape and fault shape is often overlooked by many geoscientists during the seismic interpretation phase of a project. We believe this is often due to a limited structural background by geoscientists, which restricts their understanding of fault–fold relationships. Interpretation errors related to the geometry of faults and horizons become obvious when viewed in the form of a balanced cross section. Risk can be reduced significantly by using comprehensive, balanced 3D structural models.
A validated 3D structural model not only is kinematically correct but also helps to eliminate any errors of interpreted displacement along selected fault surfaces. The elimination of displacements that are kinematically incorrect creates higher quality interpretations. Whereas a balanced 3D structural interpretation may not be unique, it does add substantially to the validity of any interpretation. From structural workstation analysis, it can be readily seen that the term balancing encompasses validation, retrodeformation, and/or restoration (see Retrodeformation in this chapter). The complexity of retrodeforming a structural cross section manually may be difficult if not impossible in many cases, yet it can be readily and accurately completed with a computer.
Two-dimensional and three-dimensional structural workstation software can significantly expand the interpretive capacity and accuracy of the geoscientist. Software links provide direct communication between structural applications and other geophysical and geological software programs. Accuracy, efficiency, and completeness are improved by the sharing of data in a workstation environment.
A comprehensive structural model incorporates all the available geological and geophysical data for a given area. In most cases, structural analysis forces the geoscientist to “fill in the blanks” beyond the limited available information. The good data areas can be readily projected into the poor data areas. Workstations can access and store volumes of data beyond the reasonable capacity or efficiency of manual manipulation.
Accurate dip analysis, sonic logs, lithology logs, deviation surveys, and all other well data are incorporated into an accurate structural interpretation. Detailed surface geology maps, including topography, provide a wealth of information for land-based study areas. All stratigraphic data are an integral part of a comprehensive structural interpretation. Computer-aided structural analysis enables you to analyze all your data accurately and completely. The accuracy and reliability of subsurface maps are enhanced and perfected with a detailed, computer-generated structural model.
Structural modeling is the keystone to subsurface modeling and visualization. Therefore, from an industrial point of view, technical and economic success ties directly to the accuracy and effectiveness of the subsurface structural interpretation. The structural analysis not only provides the framework for detailed production activities but also drives frontier exploration. Preseismic structural models are cost-effective prospecting tools during the initial phases of a study. Structural models can help in planning and guiding a seismic acquisition program and can aid in improving the quality of acquired seismic data. Digital cross sections and assigned interval velocities lend themselves to ray-tracing programs and resultant models to help facilitate the planning, acquisition, and interpretation of seismic data. The economic success of a new discovery or the cost of a dry hole dwarfs the cost of a proper structural evaluation. The process of structural modeling and restoration forces the geoscientist to critically think about the interpretation, to question the data, and to understand the hydrocarbon potential of the region. The computer-based structural interpretation allows geoscientists to quickly and accurately converge on viable geological solutions to complex structure problems.
Retrodeformation
In a previous section on classical balancing techniques, we introduced a number of powerful rules and constraints to check interpretations. These rules concerning preservation of line length and bed thickness can be quickly applied to cross sections to insure cross-section viability. We now demonstrate that bed line-length and thickness preservation is an important first step in a two-step operation of retrodeformation.
In the introduction to this chapter, we emphasize that, with time, structures move and that structural interpretations should be restorable. The process is called retrodeformation, or palinspastic reconstruction. Any interpretation of subsurface data should be restorable to an initial undeformed state because the stratigraphic units were deposited parallel to regional dip. Faults induced by compressional forces may cut the strata, causing the hanging wall beds to move over footwall beds. The structure is thrust forward and into its present position. Let us assume that this structure is presently imaged on seismic profiles. The retrodeformation process is the reverse of the forward-thrusting process. Any interpretation of the faults contained in this seismic data set should be compatible with the hanging wall beds moving back along the fault surface into their undeformed state. The pieces of the seismic puzzle should be restorable without mass overlaps or voids. These principles apply to every tectonic regime, but they are most easily applied to compressional and extensional regimes. However, the retrodeformation principle is an excellent consistency check on interpretations of compressional, extensional, strike-slip, and salt structures. We apply line-length and bed-thickness preservation concepts to a seismic line to show how these concepts can improve prospect integrity.
Examine Figure 10-9, which is taken from Bally’s (1983) classic monograms on seismic interpretation, “Seismic Expressions of Structural Styles.” In the forward to his monograms Dr. Bally states, “As to the interpretations presented, the reader will have frequent occasion to disagree or to be unconvinced of the interpretation offered. This properly reflects the fact that seismic reflection profiles are not easily interpreted in a unique way. Because the marked seismic lines are frequently supporting published papers, less critical readers often feel that such illustrations constitute geological proof, while in reality they are much more like drawings on a seismic background that illustrate an author’s concept” (our emphasis). Dr. Bally’s statement has many important consequences to industry, so let’s examine his statement in more detail.
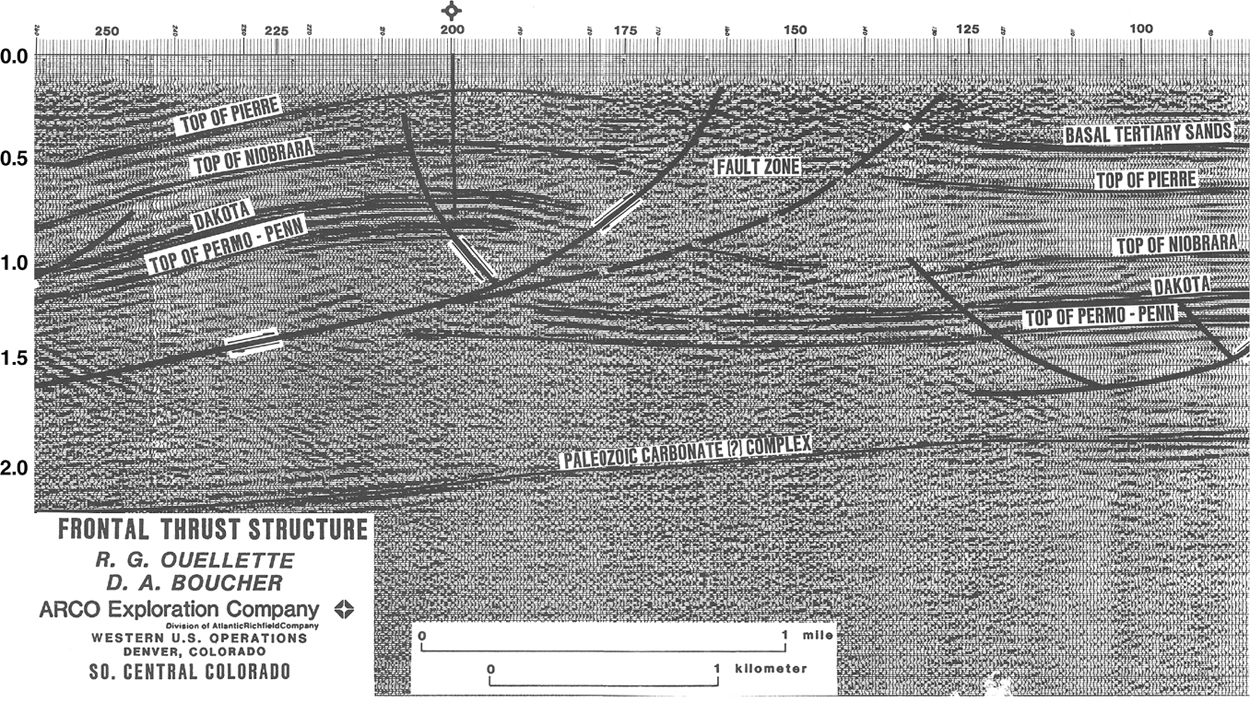
Figure 10-9 Time profile of a fold from the Colorado Rocky Mountains. Beneath the “fault zone,” dipping Niobrara reflections over flatter Dakota sandstone reflections may indicate a detachment near the level of the Dakota. (From Bally 1983; AAPG©1983, reprinted by permission of the AAPG whose permission is required for further use.)
Dr. Bally makes several important points that management, accountants, economists, and working teams should remember every time geoscientists propose a multimillion dollar well. Economics dictates that wells are expensive and that geoscientists are cheap, and not the other way around. Money should always be available to test the viability of all prospects prior to drilling (Tearpock et al. 1994).
The other concept inherent in Dr. Bally’s forwarding statement is that there are two sets of interpretations: those that constitute “geologic proof” and those that constitute “drawings.” We call the first type of interpretation an admissible interpretation (Elliot 1983). An admissible interpretation maintains 3D structural validity and is a geologically possible interpretation. The second type of interpretation is the inadmissible interpretation that does not maintain 3D structural validity and is therefore impossible on simple geometric grounds. Chapters 10, 11, and 12 concentrate on admissible interpretations as applied to prospects and prospect evaluation. With this in mind, we next test Figure 10-9 for its admissibility.
Often, during a prospect review and evaluation of compressional structures, we first check for apparent horizon thickness changes. For example, in nongrowth environments horizons should not change thickness across fault surfaces. The eye is very sensitive to vertical thickness changes and, with a little practice, can readily detect problems in the time domain. Notice on the time profile in Figure 10-9, within the front limb of the structure between sp 125 and sp 175, that the section between the top of Pierre and the top Permo-Pennsylvanian strata apparently thickens. Could this thickness variation result from higher velocity rocks thrust over lower velocity rocks or, alternatively, from imbricate thrusting? Time profiles are not geological profiles and are subject to geometric distortions. In order to remove the geometric distortions, the time section needs to be digitized and depth-corrected on a workstation.
Notice on depth-corrected Figure 10-10a that the thickness variations within and beneath the fault zone are exaggerated in the depth domain. These thickness changes are more pronounced within the “fault zone” (refer to Fig. 10-9) that was interpreted in order to retrodeform the structure. The bed dips in the fault zone exceed 40 deg. An interpretation of the depth-corrected section strongly suggests that the fault zone in Figure 10-9 results from high bed dips that are common to compressional terranes. In compressional regimes, high bed dips can result in time sections that dramatically distort structures, and we strongly recommend that all interpretations be analyzed in the depth domain. The time section in Figure 10-9 bears little resemblance to the depth section in Figure 10-10a.
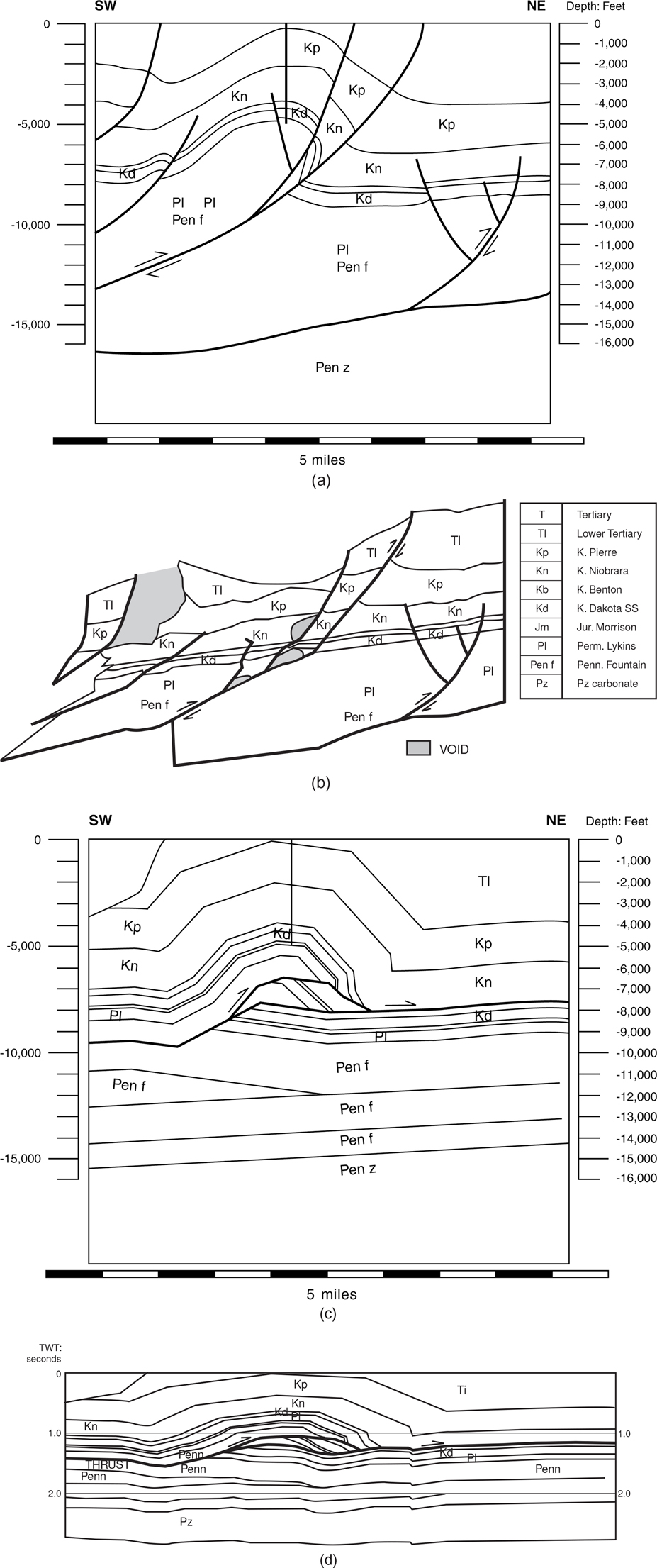
Figure 10-10 (a) Depth-corrected interpretation of time profile shown in Figure 10-9, generated using structural interpretation software. The depth-corrected figure suggests a much tighter fold than the horizontally stretched seismic profile (Fig. 10-9). In the depth domain, the frontal limb fold geometry contains unusual thickness changes above the Dakota sandstone. (b) Fault zone on Figure 10-9 correlates to region of high bed dips in this figure. (b) Retrodeformed Figure 10-10a contains voids and formation thicknesses that do not match or are not uniform across the interpreted faults. This mismatch indicates area and thickness imbalances. (c) Reinterpretation of Figure 10-9 using workstation software and structural principles. Unnatural thickness changes shown in Figure 10-10a indicated an area imbalance that may contain an untested horse block. This figure area-balances and is restorable. (d) Balanced section Figure 10-10c converted to the time domain. This figure can be compared to Figure 10-9 to check for consistency. (Published by permission of R. Bischke.)
Figure 10-10b, which represents a restoration of the depth interpretation in Figure 10-10a, shows regions of area imbalance and contains voids in the undeformed state. The horizons change thickness across the restored faults, particularly in the Pierre (Kp) and Niobrara (Kn) units, which indicates a violation of the bed-thickness conservation rule. On a properly restored thrust fault, the beds will maintain approximately constant thickness across the restored structure. This follows because the sedimentary units were deposited parallel to a gentle regional dip. One of the reasons the structure does not area-balance is that no detachment exists to produce the dipping beds above the “flat” Dakota and top Permo-Pennsylvanian strata (between sp 125 to 175 on Fig. 10-9).
How can we improve the interpretation? Refer to Figure 10-11, a profile from the Canadian Rocky Mountains (Bally et al. 1966). In the Moose Mountain sheet and in the lower central portions of the profile beneath Bow Valley is a structure that resembles the one in Figures 10-9 and 10-10. In Figure 10-11 the thrust fault is observed to ramp beneath the western limb of the fold and flatten beneath the structure’s eastern limb. This ramp-flat fault geometry is consistent with high-quality seismic data and is observed in outcrops (Boyer 1986). We use this geometry to reinterpret and balance the structure in Figure 10-9. As mentioned previously, the structure does not balance due to the lack of a detachment located between the level of the dipping Niobrara and the flatter Permo-Pennsylvanian formations. Applying Dahlstrom’s rule for picking thrust faults (dipping beds over flatter beds) to the time or depth section, we proceed to balance the structure. The results, shown in Figure 10-10c, require an imbricate fault block, or horse, which is common to fold-thrust belts (Boyer and Elliot 1982). This solution is interesting in that the structure could possess additional hydrocarbons on the level of the repeated Dakota sandstone within the horse. A ramp-flat fault geometry, when applied to Figure 10-9, results in an admissible interpretation, as shown in Figure 10-10c.
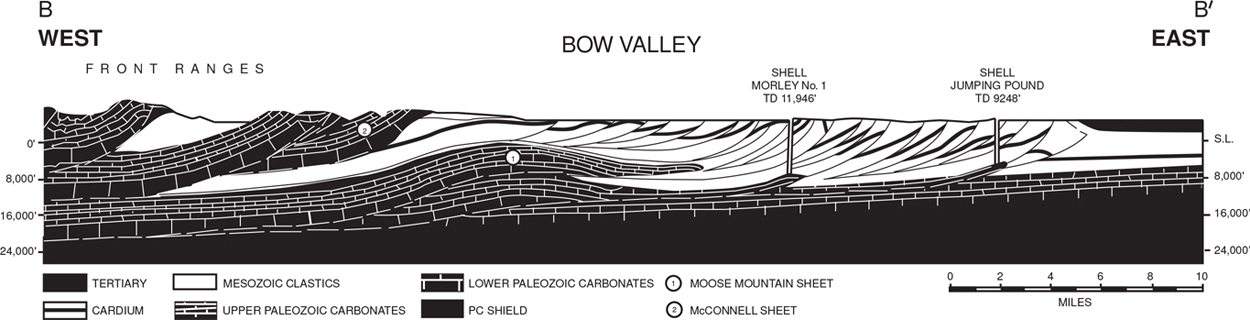
Figure 10-11 Balanced cross section of Canadian Rockies showing ramp-flat fault geometry (From Bally et al. 1966. Published by permission of the Canadian Society of Petroleum Geologists.)
Lastly, we convert Figure 10-10c back to the time domain in Figure 10-10d. You can now compare Figure 10-10d to the original time section (Fig. 10-9).
All interpretations of prospects have consequences, which may influence the success of a project and the interpretation of the petroleum system. In Figure 10-9 a possible fault trap exists beneath the fault zone in the upturned beds of the Dakota sandstone. Figure 10-10c indicates that the trapping fault may not exist and that the Dakota strata maintain stratigraphic thickness and may not turn up beneath the proposed fault. This affects prospect risk. The balancing software also predicts the position and thickness of the horizons that are missing from Figure 10-9.
Figure 10-10c predicts that the thrust fault beneath the fold continues toward the northeast to possibly link to other prospects in the petroleum system (Boyer and Elliot 1982). Figure 10-9 suggests that no such link exists in the system, which also affects migration risk.
Locating Thrust Faults on Dip and Strike Lines
Picking Thrust Faults on Dip Lines
Picking thrust faults on seismic sections is not as straightforward as it may seem. This subject is complicated because thrust faults are typically “thin skinned” and may follow, or parallel, bedding surfaces over long distances (Rich 1934; Bally et al. 1966).
A major insight into picking thrust faults came from the Canadian Rockies, where petroleum structural geologists noticed in outcrops of thrust faults that steeply dipping beds overlie flatter dipping beds (Bally et al. 1966). In the discussion of pin lines, we show this bed dip discordance or discontinuity in Figure 10-5c and called this method for picking faults Dahlstrom’s rule (Dahlstrom 1969). The method works for both dip lines and strike lines.
In Figure 10-12, we can observe a thrust ramping to the left of the fold hinge. The dashed line represents an axial surface, which bisects the limbs of the syncline. The outcrop is perpendicular to the strike of the fault and therefore in the dip direction. To the left of the synclinal axial surface, steeply dipping beds overlie flatter dipping beds, showing a discontinuity and a thrust fault. The thrust in the left part of Figure 10-12 represents a dip ramp, or the area near axial surface BY in Figure 10-37. Alternatively, dipping beds over flat beds can also be observed at the front of the fold, or the region between axial surfaces AX and A′X′ along the upper flat in Figure 10-37c. A similar relationship exists on seismic lines in the strike direction of the fault.

Figure 10-12 Ramp in a thrust fault from the Canadian Rocky Mountains. Dipping beds over flatter beds and the synclinal axial surface define the structural ramp. (From Boyer 1986. Published by permission of the Journal of Structural Geology.)
The 3D Interpretation of the Waha Field, West Texas
The Waha and Coyanosa Fields lie along a series of north-south striking thrust faults that uplift the western edges of the Central Basin Platform, Texas, and along the generally deeper eastern boundaries of the Permian Basin (Shumaker 1992). The Coyanosa Field is 10 mi south of the Waha field and contains distinct overturned (inverted) beds constrained by well control and described by Mitra and Mount (1998).
Figure 10-13 is a 3D north-south striking line through the Lower Ordovician, Devonian, and Mississippian beds of the Waha gas field, perpendicular to the dip of the thrust faults (Shumaker 1992; Hardage et al. 1998; Mitra and Mount 1998). This field is well known not only for its Ellenberger Group production but, according to Hardage et al. (1998), for an east-west cross section originally constructed by Mobil (Railroad Commission of Texas, Case No. 8-83) and later reworked by Kosters et al. (1989) and (Hardage et al. 1998). This cross section shows highly faulted and folded, vertical, overturned beds, typical of fault propagation folds (Fig. 10-14a and b). Twenty wells penetrate the main body of the structure, thus providing adequate data for well log correlations (Fig. 10-16). This 3D line was chosen because it clearly images a lateral ramp structure on the northern flank of the Waha Field. Another lateral ramp, from the El Furrial Field, North Monagas, Venezuela, is shown in Figure 10-51b.

Figure 10-13 Three-dimensional strike line imaging a lateral ramp across the Waha Field, Permian Basin, Texas. This line is tied to the cross section shown in Figure 10-15. (Published by permission of the Bureau of Economic Geology, University of Texas at Austin; edited by Hardage et al. 1998.)

Figure 10-14 Three-dimensional model of a fault propagation fold of a lateral ramp. (a) On this figure, the lateral ramp is displayed on the vertical plane in the strike direction on the flank of structure. (b) To expose the lateral ramp geometry, the frontal horizons are removed up to the vertical plane, exposing the thrust fault and the horizons dipping onto the thrust fault. (Published by permission of R. Bischke.)
On the northern flank of the 3D line, dipping reflections from 1750 ms to 2750 ms overlie flat dips below 2750 ms (Fig. 10-13). Provided that the dips exceed about 5 deg (see discussion at the end of this section), this relationship of dipping reflections over flat reflections is typical of deformed horizons above reverse faults (Fig. 10-5c) (Dahlstrom 1970). Structural geophysicists use these discontinuous relationships to pick and accurately map thrust faults. In this case, the base of the faulting is picked and interpreted at about 2750 ms. This interpretation is consistent with Kosters et al. (1989) (Fig. 10-15) cross section, which terminates near Well No. 75 (see Fig. 10-16). The 3D strike line is on the back limb of the structure and ties to Well No. 74 on Kosters et al. (1989) cross section (Fig. 10-16). Well No. 78, located 4000 ft (1200 m) south of the Well No. 72, contains more than 2000 ft of overturned Ordovician Simpson section (Fig. 10-15).
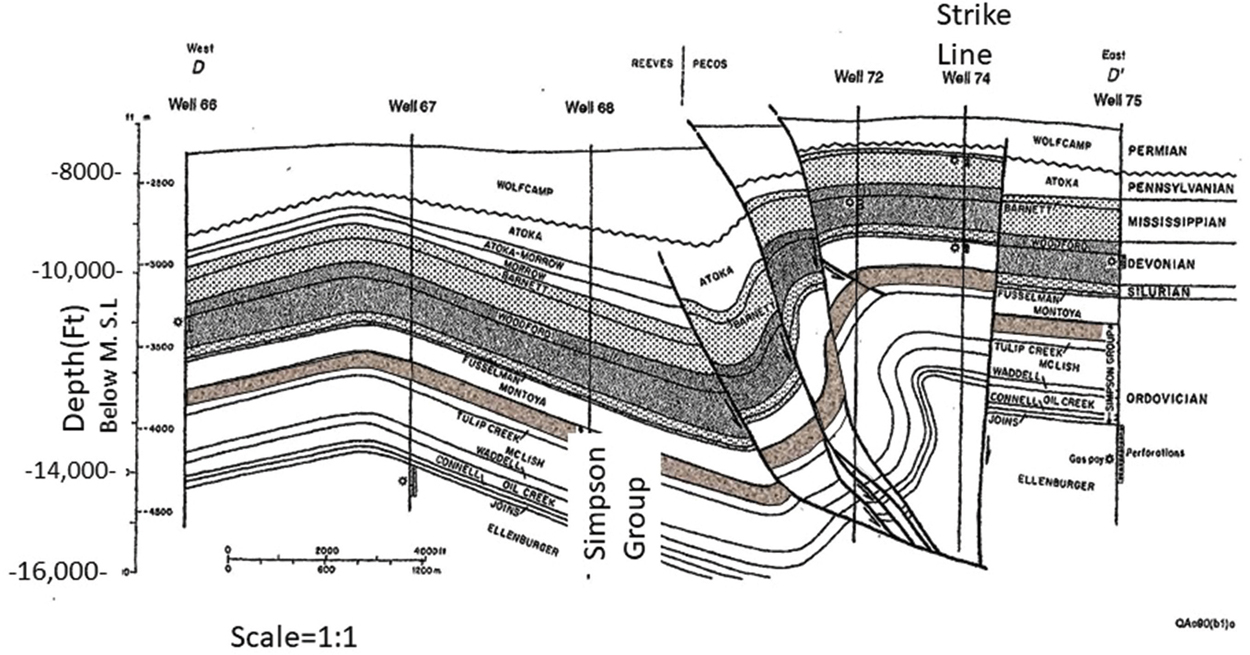
Figure 10-15 East-west cross section of the Waha Field, Permian Basin Texas, in the vicinity of Wells No. 72 and No. 74. This complex cross section is based primarily on well control; the Waha Field contains several large reverse faults and a 3000 ft (914 m) long section of near vertical beds in Well No. 72. (Modified from Kosters et al. 1989. Published by permission of the Bureau of Economic Geology, University of Texas at Austin; edited by Hardage et al. 1998.)
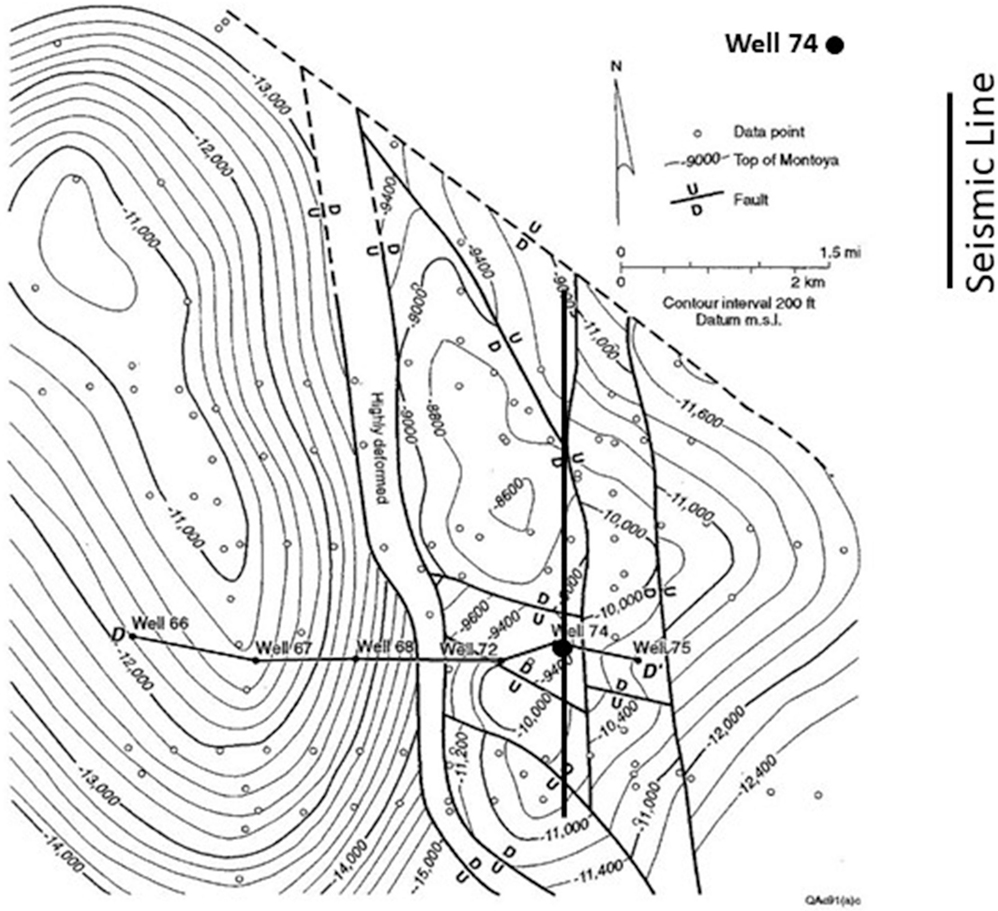
Figure 10-16 Structural-depth map showing wells crossing Figure 10-15, which is the east-west cross section across the Waha Field, Permian Basin, Texas. The direction of the north-south lateral ramp shown on seismic line (Fig. 10-13) is drawn on the figure through Well No. 74. (From Hardage et al. 1998. Published by permission of the Bureau of Economic Geology, University of Texas at Austin.)
The strike line shown in Figure 10-13 images what is defined by industry as a lateral ramp. In other words, the north-south directed strike line images the north dipping reflections on the flank of the structure. These reflections terminate against an east-west dipping thrust ramp (consult section Fault Propagation Folds and Fig. 10-43). A 3D model showing these relationships is shown in Figure 10-14 and is described in detail in the next section.
The lateral ramp imaged in Figure 10-13 has about 600 ms of structural relief. Seventeen wells in or near this structure have checkshot data, and thus a well-constrained velocity/depth function exists for the area (Hardage et al. 1998). Using this function and Well No. 72 between 1750 ms to 2350 ms yields about 4500 ft (1370 m) of structural relief. This value of 4500 ft of structural relief on the lateral ramp is consistent with Kosters et al.’s (1989) cross section (Fig. 10-15), as the well log data suggest that the thrust fault deepens as it dips to the east beneath the crest of structure, which is flat.
Furthermore, on the crest of structure is Well No. 72 that encounters five reverse faults (Fig. 10-15). Kosters et al.’s (1989) interpretation of this well log data is that the logs contain 4300 ft (1310 m) of log offset (repeated section and vertical and overturned beds) (Hardage et al. 1998). The reverse faults located at 1800 to 2100 ms are small and repeat 140 to 280 ft of section. The horizontal black-colored fault interpreted on Figure 10-13 is the largest fault with about 850 ft (260 m) of repeated section and is located near the base the of the structure in Well No. 72. Also, the McLish formation in the well has 3000 ft (915 m) of near vertical to overturned beds (Fig. 10-15).
Three-Dimensional Models of Lateral Ramps
Three-Dimensional Fault Propagation Fold Model.
Figure 10-13 images a 2D seismic line. Three-dimensional geometric images of lateral ramps maybe difficult to visualize but are important for correctly defining thrust fault surfaces and constructing accurate maps. The reader may want to study the 3D models of lateral ramps shown in the color Figures 10-14 and 10-17. These figures do not include the bed on the top or crest of structure. We discuss a 3D fault propagation model before studying a 3D fault bend fold model.
Figure 10-14a is a modeled fault propagation fold displayed in two dimensions but missing the crestal bed, which is flat at the top of structure. Figure 14a (top) is a modeled lateral ramp and is similar to the left-hand side of Figure 10-13 in that Figure 10-14a (top) trends in the strike direction. Notice that the laterally dipping beds terminate on a horizontal trust fault, as do the less coherent beds, just below the yellow line in Figure 10-13 (also consult Fig. 11-51b for a coherent example). Two-dimensional Figure 10-14a (bottom) trends in the dip direction and is similar to Figure 10-15.
Figure 10-14b is a fault-propagation fold model showing the flank, thrust fault, and horizon dip relationships in three dimensions. The model is bound on the right-hand side by a 2D profile of a fault-propagation fold (see Fig. 10-14a [bottom]). The crest of structure occurs on the horizon above the green horizon (consult Fig. 10-43). The model shown in Figure 10-14b does not contain the beds above the crest, as the beds above the crest would not be faulted, and the thrust would be buried by the shallower horizons. This buried thrust fault would be called a blind fault. The small fault located at depth and near the termination of the flank (on the far-left side of the structure) has less slip on its surface and is blind, or buried by the green and clear horizons. The crest of structure would be to the right of the 2D fault propagation fold shown in Figure 10-14b.
Next, we discuss the 3D geometric properties of the lateral ramp. On Figure 10-14b, the vertical plane trends across the flank of the structure, displaying the green to orange horizons and the lateral ramp thrust geometry (compare Fig. 10-14a and 10-14b [top]). The green to orange horizons to the front of the vertical plane have been removed, thus displaying a horizontal thrust fault on the vertical plane and the dipping flank horizons. In two-dimensions, this is the upper figure in Figure 10-14a. This vertical plane, which contains the green to orange horizons, is on the flank of the structure and is in the strike direction.
Notice that the horizons intersect and terminate onto the thrust fault. This vertical plane is perpendicular to the dip direction. The termination is most obvious on the thin clear and orange horizons. As these lateral or flank horizons terminate at the thrust, the dipping beds create a discontinuity in the horizons. This discontinuity occurs where dipping beds overlie a flat horizon. By definition, this displacement discontinuity defines the lateral fault geometry, and industry has called these geometric relationships Dahlstrom’s rule (Fig. 10-5c, Dahlstrom 1970).
Three-Dimensional Fault Bend Fold Model.
The 3D model for lateral ramps on fault bend folds is not as complicated as the 3D model for fault propagation folds (Fig. 10-17a and b). As with the fault propagation fold model (Fig. 10-14b), the right-hand side of the model contains a 2D model of the structure, but in this case, a 2D fault bend fold (see Fig. 10-17b [bottom]).
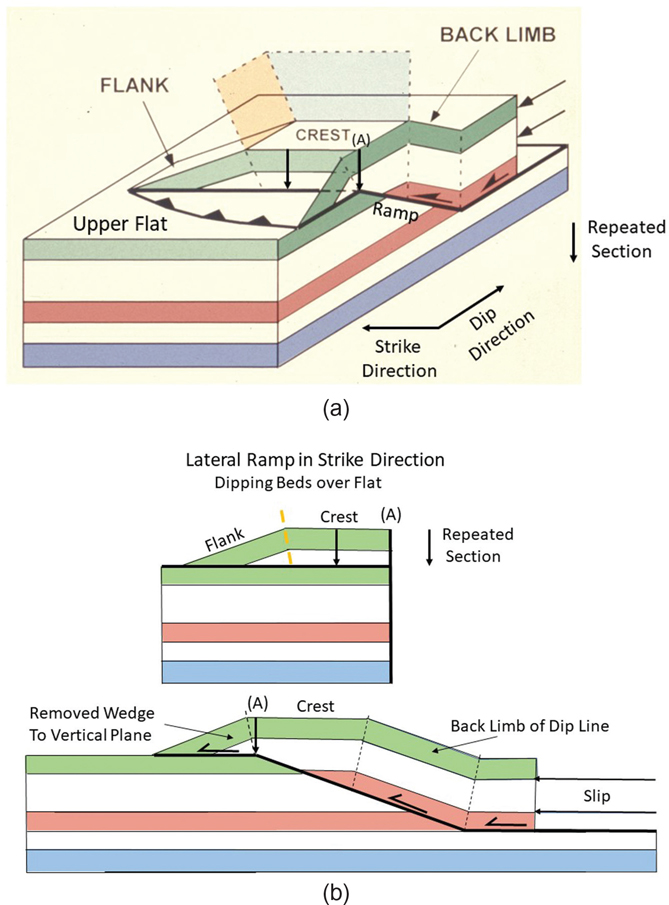
Figure 10-17 (a) Three-dimensional model of a fault bend fold with the frontal limb removed. The barbed line on the footwall, upper flat, depicts the contact of the thrust fault with the removed frontal limb. The repeated section from the crest of structure in the hanging wall to the footwall is the vertical arrow, which points to the thrust fault at the base of the arrow. (b) Two-dimensional model of a fault bend fold moving up a ramp in the dip and strike direction. Strike direction is the top figure, and dip is the bottom figure. (Published by permission of R. Bischke.)
The horizons to the left of the frontal limb of the 2D fault bend fold are removed (i.e., the horizons to the left of the frontal, dipping 2D green horizon in Fig. 10-17a). The frontal and dipping green horizon above the upper flat terminates onto the upper flat, creating a discontinuity that defines the thrust (Fig. 10-17a). At the top of upper flat, the horizontal fault follows the upper flat to the top of the thrust ramp. The horizons above the upper flat were removed to expose the uppermost portion of the ramp, thus exposing the thrust fault at the top of the ramp. The exposed portion of the thrust fault is the horizontal line in Figure 10-17a, which terminates on the upper flat. Also shown on the upper flat is the frontal position of the thrust, which dies out at the left-hand side or flank of the structure. The slip on the thrust increases to the right, with the slip reaching a maximum at the dipping green horizon (the curved hashed line).
The lateral ramp is defined by the dipping green horizon, which forms the flank of the structure in Figure 10-17a and in 2D Figure 10-17b (top). Its significance is that the dipping lateral horizon forms a displacement discontinuity with the upper flat and thus by definition forms a fault. To reiterate, this discontinuity terminates the dipping horizons onto flat horizons, defining Dahlstrom’s rule, that thrusts exist where dipping beds terminate against flatter dipping beds (Fig. 10-5c, Dahlstrom 1970).
Distinguishing Structural from Stratigraphic Dips
A question may arise as to how to distinguish stratigraphic dips from structural dips. We first refer to Rich (1951), who found that clinoforms in the steeply dipping portions of deltas rarely exceed 5 deg. Second, clinoforms reflect downlap or toplap. Thus, if the seismic reflections are folded and dip at angles exceeding about 5 deg, then the dips are most likely structural and not stratigraphic. Oceanic bed dips tend to be small, and the continental slope tends to dip at less than two degrees. Also, remember that interpreters construct horizontally compressed (vertically extended) seismic sections in order to image subtle changes in dip. Thus, it is always wise to construct several seismic lines at a scale of about one to one from regionally generated velocity functions to view the structure on a less distorted scale.
We also recommend that you use the workstation to scan the strike direction looking for lateral ramps along the flanks of folds. If such a strike ramp is located in the data, pick the fault on several strike lines and construct an initial fault surface map. To complete the fault interpretation and fault surface map, tie the fault surface to the dip lines.
Cross-Section Consistency
So far, we have generalized the concept of brittle or frictional deformation to a 2D cross section. As deformation is three-dimensional, the brittle deformation interpreted on one cross section imposes constraints on interpretation of the adjoining cross sections, such that the interpreted folds or faults must not terminate abruptly. However, the deformation can be dissipated gradually. In other words, fault slip must be consistent, although not necessarily conserved, from cross section to cross section. Also, the slip can decrease to zero as the result of deformation in the cores of folds.
For example, if a cross section of a complex structure exhibits three thrust faults with a total of 3 mi of slip, then it is very likely that a nearby cross section will also contain three thrust faults of similar shape and form that also contain about 3 mi of slip. If these three thrust faults radically change position and/or shape, then some intervening transverse structure must exist to accommodate the deformation. Such intervening structures are called transfer structures, and these structures exist in compressional (Dahlstrom 1969) as well as tensile extensional environments (Gibbs 1984). Transfer structures often occur as tear faults, or cross faults, which form at high angles to the major structural trend. Furthermore, these transverse structures are often responsible for changes in the trends and shapes of structures from cross section to cross section. Figure 10-18 illustrates a transfer by lateral shear from one fault bend fold to another. In Figure 10-18a, the displacement on Fault 1 is compensated by displacement on Fault 2 (see left side of diagram, Fig. 10-18a). The sum of the displacements on Fault 1 and Fault 2 remain constant; thus, as the slip on Fault 1 decreases, the slip on Fault 2 increases. The amplitude of the folds above the faults also change in a like manner. On profile F, the slip on Fault 1 is equal to the slip on Fault 2, and the folds that form above the two faults have the same amplitude. The resulting structures caused by the lateral shear are shown in map view in Fig. 10-18b. The result is that the fold on Fault 1 plunges to the south and is replaced by the fold on Fault 2, which plunges to the north. This slip transfer between folds is very common in fold-thrust belts (Fig. 10-19).
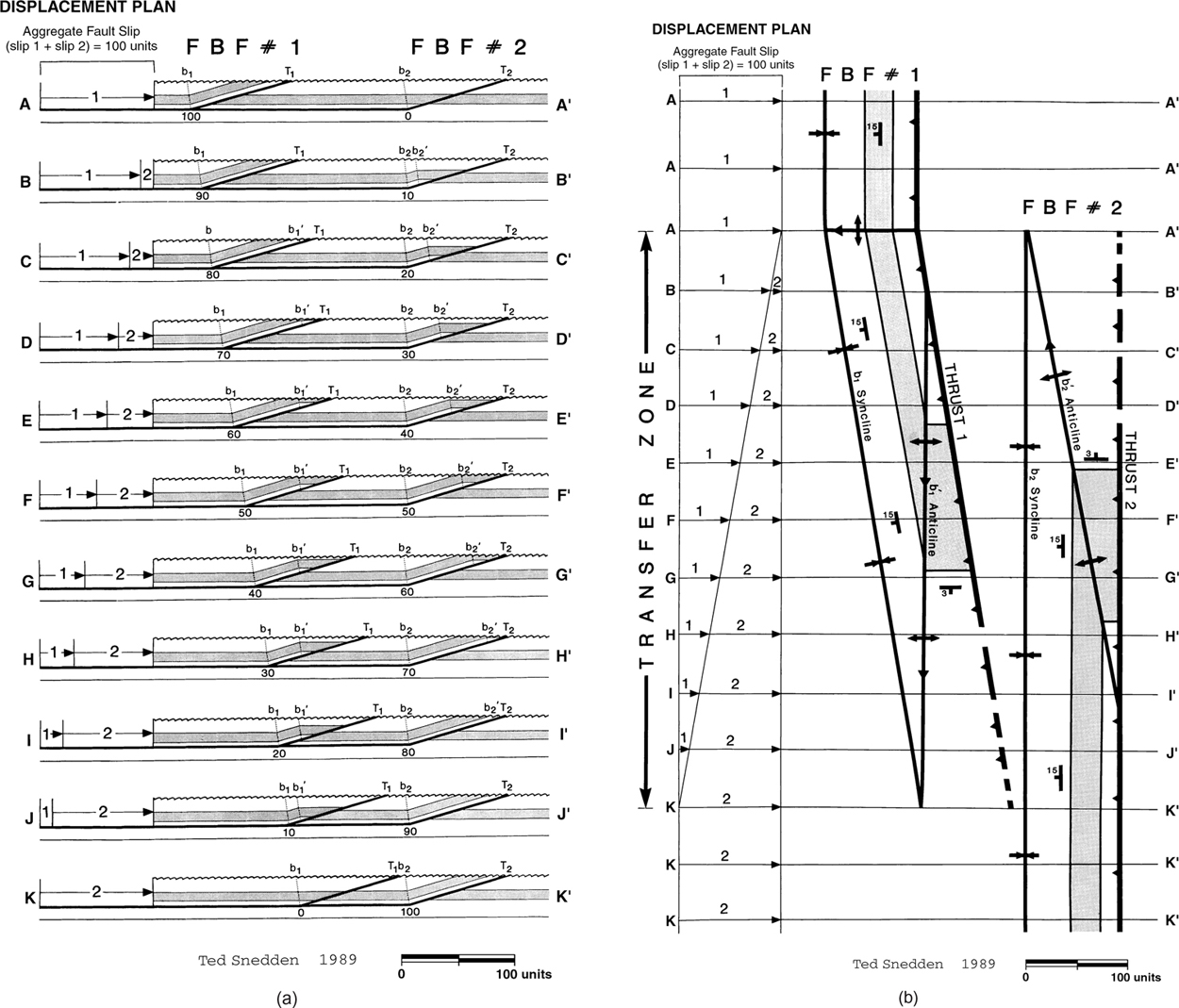
Figure 10-18 (a) A cross section of a transfer zone from one fault bend fold to another. (b) A top to down view of (a), similar to the aerial radar aperture image of the Appalachian fold-thrust belt shown in Figure 10-19. (Published by permission of Ted Snedden.)

Figure 10-19 Radar aperture image of Appalachian fold-thrust belt near Harrisburg, Pennsylvania, showing an echelon arrangement of plunging anticlines. This displacement transfer is common to fold-thrust belts. Although repeated section exists in the well logs from this area, notice the near absence of surface faulting. The absence of surface faulting is common to portions of many fold-thrust belts, where the deep thrusts occur as blind or as bedding plane thrust faults. (Published by permission of the United States Geological Survey.)
Therefore, we see that small changes are permissible from cross section to cross section, but how much change is possible? Elliott (1976) was the first geoscientist to attempt an answer to this question with the bow-and-arrow rule (Fig. 10-20). Additional studies suggest a linear scaling between displacement and fault length (Davis et al. 2005; Bergen and Shaw 2010). Elliot’s rule states that the amount of displacement can vary along a fault zone, but at an amount equal to 7% to 12% of its strike length. For example, suppose you mapped deformation along a large thrust fault zone that has a total length of 10 mi. From the bow-and-arrow rule, one would predict that the maximum dip-slip motion on the fault would be on the order of 0.7 mi to 1.2 mi. Next, assume that the amount of displacement along another fault is known to increase to a maximum along a 10-mi portion of the fault zone. We can now predict not only that the fault is at least 20 mi long but also that there are at least 1.4 mi to 2.4 mi of dip-slip motion on this fault. The bow-and-arrow rule is based on scaling laws, and it follows that laterally restricted faults have small displacements, whereas only laterally extensive or long faults have large displacements.
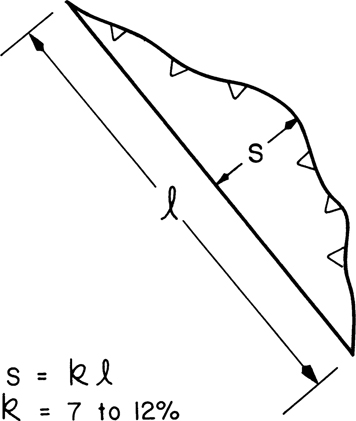
Figure 10-20 Bow-and-arrow rule. Slip perpendicular to fault strike is approximately 10% of the fault length. (Modified after Elliott 1976. Published by permission of the Royal Society of London.)
Bergen and Shaw (2010) used high-quality seismic data to map fault surfaces in order to predict a fault length (L) versus a maximum displacements (Dmax). Their work suggests that a near linear relationship exists in the form of a power law relationship, where
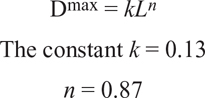
from three different data sets with an R2 = 0.89. For n = 1.0, the equation simplifies to Dmax/L = k, and thus the Bergen-Shaw equation is near linear.
Bergen and Shaw carefully studied their displacement-length profiles and from this hard data came to a conclusion that many geoscientists who map faults would support. They concluded that if two growing faults are roughly on strike with each other, the two faults may merge and that “folding and fault linkage [are] the probable causes of much of the variation in displacement-length scaling ratios observed in our data sets” (Bergen and Shaw 2010). Our fault surface mapping results based on numerous field and exploration studies supports Bergen and Shaw’s conclusions that “fault interactions play a major role in the ultimate displacement profile geometries for thrust faults.” Furthermore, we believe that any scaling equation not based on tied fault surface mapping and the fault linkage concept is questionable (Chapter 9, section Fault Interpretation Strategies).
Elliott (1976) developed the bow-and-arrow rule for thrust faults, and a similar relationship may exist for normal faults, particularly for faults in excess of 10 mi in length (Morley 1999). However, no consensus exists for normal faults, as different studies based on different approaches have generated different conclusions.
Cross-Section Construction
Extrapolation of dip data to depth is a critical aspect of interpreting structures that may contain hydrocarbons and of accurately predicting wellbore results. The data can be in the form of outcrop dips, stratigraphic unit tops and bases taken from outcrop or well logs, dipmeter data, and depth-corrected seismic data. There are presently two methods available for extrapolating dip data to depth: the Busk method of segmented circular arcs (Busk 1929) and the kink method, which stresses the long planar limbs exhibited by most folds (Faill 1969, 1973; Laubscher 1977; Suppe 1985; Boyer 1986). Both methods assume that the folding is parallel; that is, stratigraphic unit thickness remains constant (in the absence of more detailed information). The Busk or the kink method can be used to extrapolate any type of dip data. It is important, however, to be consistent in the use of the data. For example, the top of a stratigraphic unit is projected to the top of an adjacent unit only if the units being mapped do not change thickness, which is commonly the case over short distances. A dipmeter recording within a stratigraphic unit is not projected to a dipmeter reading in an adjacent well unless these recordings are on the same stratigraphic level. In other words, it is important to understand that you are projecting time-stratigraphic surfaces across the structure.
Busk Method Approximation
The Busk method (Busk 1929) assumes that the folds are parallel (constant-thickness of stratigraphic units) and that they are concentric; that is, the folds consist of segments of circular arcs. These arc segments are used to project data to depth. Normally, dip data measured from surface outcrops, well logs, or seismic sections will not lie along the plane of cross section. Thus, the data must be projected to the plane using the methods discussed in Chapter 6. Let us assume for simplicity that the data, measured from outcrop, are shown in Figure 10-21a. The data points are usually defined on specific stratigraphic unit tops or bases. Normals (lines perpendicular to dip) are drawn downward from the position of the dip measurement data. These normals intersect at a point that represents a radius of curvature for an arc (point O in Fig. 10-21b), which is used to project the stratigraphic data in the area between the two data points A and B. A compass centered at point O is extended so that it has a radius OA, and then an arc is constructed from point A to line D (Fig. 10-21c). This procedure is then repeated for point B, using radius OB. The results of this exercise are two concentric arc segments, AE and FB, which define a curved layer AE-FB, of constant thickness AF, or EB. If another data point G is introduced (Fig. 10-21d), the normal to this adjoining data point will intersect line segment OB at a different location, point O, and now several different radii (O′B, O′G, OI) are used to complete the stratigraphic extrapolation. In Figure 10-21e, a well with dipmeter data is added, and more normals and arcs are drawn to depict a more complete fold.
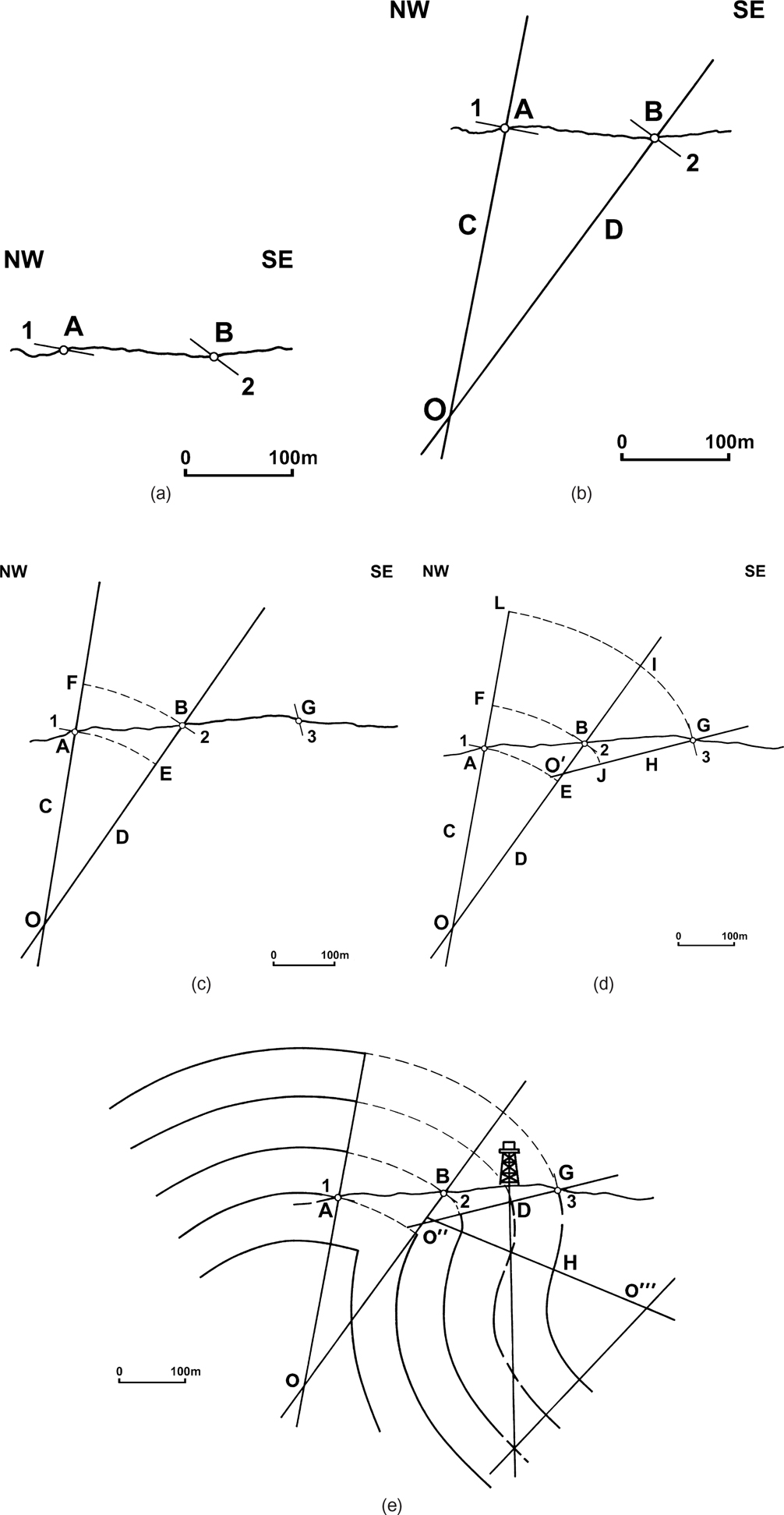
Figure 10-21 (a)–(e) Busk method approximation. The strata are projected to depth along segments of circular arcs. (Modified from Marshak and Mitra 1988.)
The method can be visualized as consisting of several adjoining regions, or domains, in which the curvature of the beds is constant, and at the intersection of these domains, the curvature of the beds changes. The Busk method is therefore a curved dip domain method. It suffers from an inability to retrodeform easily and to correctly project the front limb of a fold into the adjoining syncline.
Kink Method Approximation
The next method that has proven extremely useful for extrapolating data to depth or along a cross section is the kink method, or constant dip domain method (Faill 1969, 1973; Laubscher 1977; Suppe and Chang 1983). In the Busk method, bed dips that are mutually related are assumed to represent a common curvature domain. However, we could have just as readily bisected the angle between the dips from two adjacent dip data points and created two regions of constant dip related to the two data points. In the limit, or where the data are closely spaced, both methods would be identical.
As shown in Figure 10-22a, the first task in the kink method is to project the bed dip data in cross section. For example, the dip at point B is projected in the direction of bed dip data point A. Next, place two triangles adjacent to each other so that the upper triangle (X) is parallel to bed dip A and can be moved over the lower triangle (Y). (If preferred, a parallel glider can be used in place of two triangles.) Now move the upper triangle upward past the bed dip data point B and construct a line CD so that point D is approximately halfway between bed dip points A and B (Fig. 10-22b). When working with real data, point D need not be halfway between points A and B, and its position will depend on where the beds change dip. This position can often be determined from outcrop or depth-corrected seismic data. Bisect the angle between lines CD and DB with a protractor or compass, and then project the dip data at A to the dip domain boundary line with the triangle (line AE, Fig. 10-22c). Move the triangles to a new position so that one of them is parallel to dip data point B, and move this triangle down to continue line AE into the domain of dip data point B (line EF, Fig. 10-22c). The projection process results in two dip domains with each domain containing a constant dip and a theoretical interval of constant thickness (DE). Repeat the process as additional data are introduced (Fig. 10-22d). Notice that in Fig. 10-22d, dip domain B converges and terminates at point O, which is called a branch point. A branch point occurs at the intersection of two axial surfaces. A dip domain is eliminated at a branch point, in this case dip domain B. Only two dip domains exist beneath the branch point, whereas three domains exist above the branch point. Notice that the axial surfaces bisect the bed dip domains both above and below the branch points. It is important to remember to bisect the angle between the fold limbs and not the angle between the axial surfaces.

Figure 10-22 (a)–(d) Kink method approximation. The sedimentary beds are projected to depth along planar surfaces. The method applies to the majority of folds, which possess subplanar limbs.
In many folded areas, extensive regions of relatively constant dip adjoin smaller regions of rapidly changing dip. This is commonly seen on seismic sections. These relationships suggest that many folds possess limbs that have a uniform or near-constant dip but have hinge zones that are curved. As a result of this uniformity in dip, the kink method is readily adapted to work in low-temperature fold belts.
When applying the constant dip domain method, always remember to bisect the angle between the bed dips, thereby creating two adjoining and individual dip domains. Usually, the data are generalized or averaged to eliminate aberrant data points. This can be accomplished by taking two triangles and aligning them so that the top triangle can be passed across the data. In this manner, the triangle can be used as a filter to generalize or average the data. Areas of different generalized dip are defined as individual or separate dip domains, and the dip is then assumed to be approximately constant within each domain. The method also works very well with depth-corrected seismic or well data. The bisection procedure is in fact the continuity principle as applied to balancing (Suppe 1988) (Fig. 10-23):
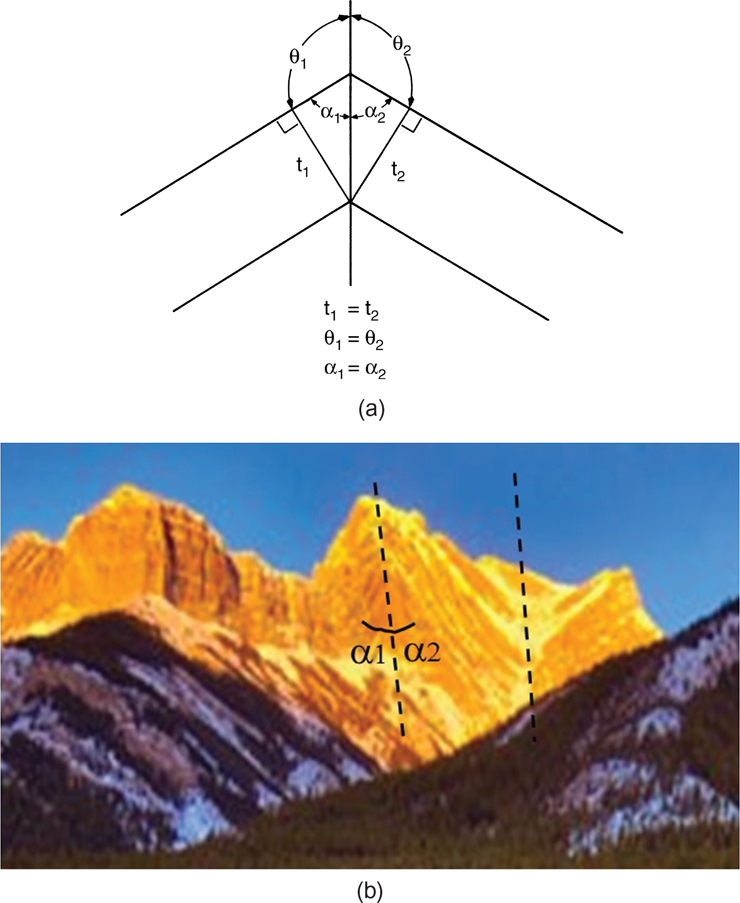
Figure 10-23 (a) Kink method geometry. (After Suppe 1980, 1985.) (b) An outcrop showing a kink band geometry. (b) A kink axial surface in outcrop.
Notice that if the fold does not change thickness across the axial surface, then t1 = t2 and α1 = α2. If this procedure is judiciously applied, the cross section is more likely to line-length balance and area-balance.
When mapping using the kink method, you will find that as the stratigraphic intervals change thickness, the theoretical structural level of the interval as predicted by the method will deviate from the observed level. Thus, periodic adjustments in bed thickness must be made, usually at the position of the axial surface, which is the dip domain boundary line (Fig. 10-22c). Our preference is to follow the observed stratigraphic unit or sequence boundary in regions of onlap, and so on, even though this results in a divergence of once-parallel lines. If units above the unconformity do not change thickness dramatically, little harm is done by accurately representing the strata.
In areas of good data, the bisected dip domain data will ensure proper line-length and area balancing. In regions where the data are poor or nonexistent, the kink method can be used to project the units being mapped. Even under these conditions, the uniform thickness assumption can be a very powerful tool. Assume, for example, that you are mapping units A and B in Figure 10-24 from the north but that you encounter a region where no data exist. Mapping toward the no-data area from the south results in a good match on unit A but a poor match on unit B. What would you conclude in this case? The mismatch could result from either a dramatic change in thickness or an unrecognized fault in the south-central area that ceased growth prior to the deposition of unit A.
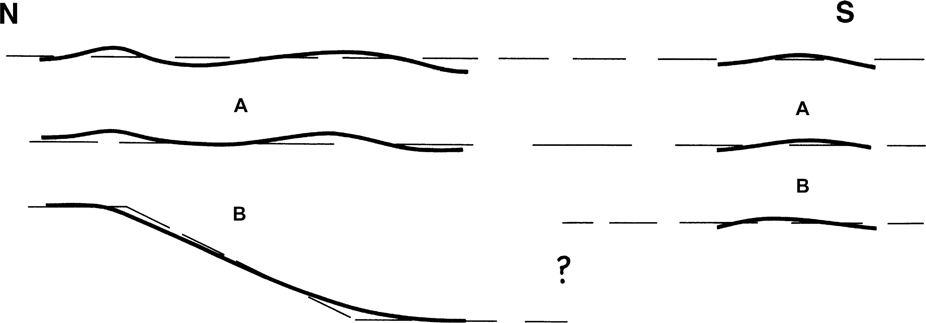
Figure 10-24 Example utilizing the uniform thickness approximation. Major change in the thickness of unit B, but not in unit A, implies that a structure or a stratigraphic change is present in the region that lacks data.
Kink Method Applications
An immediate application of the kink method arises when drilling the crests of the symmetric monoclinal or asymmetric folds that are common to fold-thrust belts worldwide (see the Fault Bend Folds and Fault Propagation Folds sections in this chapter). The improper positioning of wells on the crests of anticlines can result in drilling wells off-structure or wells into synclines (Bischke 1994a). This is particularly true when drilling into an asymmetric fold (fault propagation fold). In order to avoid costly mistakes, the compressional regime requires a good understanding of structural styles and geometry.
Figure 10-25 shows two different interpretations of an asymmetric fold based on the same bed dip data and seismic data. The steeply dipping limb of the fold was not imaged. Notice that the crests of the folds near the surface are positioned the same (use the dip data points as a reference). However, proposed wells are spudded at different locations based on the anticipated structural high at the reservoir level. Which well is more likely to be successful?
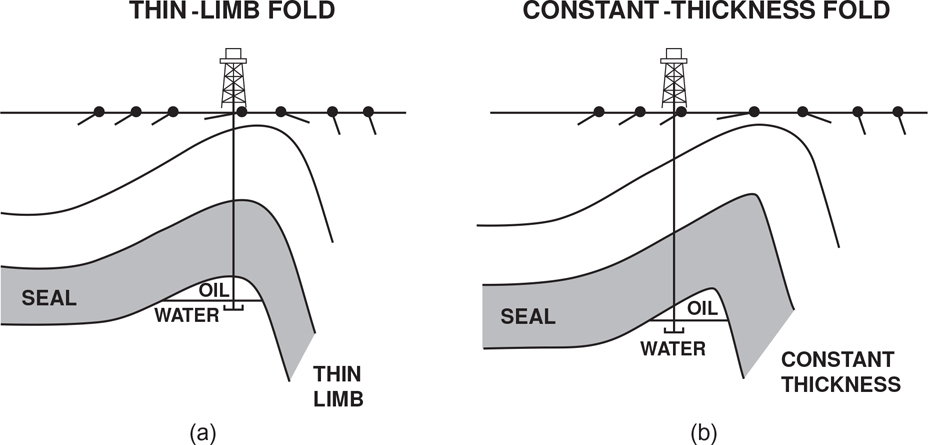
Figure 10-25 Different fold interpretations can result in different proposed well locations. (a) Interpretation of a fold based on surface dip and seismic data, but not using the kink method. An attempt was made to maintain the vertical thickness of the beds within the steeply dipping front limb of the fold (see Fig. 10-26). (b) Interpretation of a folded structure based on surface dip and seismic data and using the kink method. An attempt was made to maintain the stratigraphic thickness of the beds within the steeply dipping front limb of the fold. (Published by permission of R. Bischke.)
Figure 10-25a illustrates a well, positioned near the crest of the fold, which is interpreted to have a steeply dipping front limb. Developing folds verge or move in the direction of steeper bed dips (Fox 1959; Suppe 1985), so the steeper fold limb is defined as the frontal limb in a fold train. The front limb is interpreted in Figure 10-25a to be thinner relative to the more gently dipping back limb. This style of folding is common to high-temperature mobile belts, which do not contain petroleum reserves.
A different type of fold is the parallel, or constant-thickness, fold (Ramsey 1967) interpreted in Figure 10-25b. The beds do not significantly change true stratigraphic thickness from the back limb to the front limb. This type of fold is common to the low-temperature petroleum regime. The interpreters positioned the well on the gently dipping back limb of the structure, in a position farther left than the well in Figure 10-25a.
On seismic time profiles, stratigraphic intervals of constant thickness maintain about the same vertical time thickness. In our example, the depth profile shown in Figure 10-25a is similar to a time profile on which the interpreters attempted to maintain the same vertical time thickness of the intervals. The result is a thin-limb fold. On the other hand, the geoscientists who constructed Figure 10-25b made their interpretation on a time profile and then properly depth-corrected it to generate the depth profile shown in the figure. True stratigraphic thickness was maintained, and the result is a parallel fold.
Geoscientists who work fold-thrust belts know a majority of the folds within hydrocarbon-producing regions approximate parallel folds rather than thin-limb folds (Suppe and Medwedeff 1990; Tearpock et al. 1994). Unless data exists in support of a thin frontal limb, the parallel fold interpretation is likely to be the better interpretation.
If the fold is a constant-thickness fold, then the likely result after drilling the two wells is shown in Figure 10-26. In the figure, the two well positions shown in Figures 10-25a and b are redrawn on the constant-thickness fold shown in Figure 10-25b. The well on the right is positioned using the thin frontal limb interpretation. This well is likely to encounter steeply dipping beds in the seal horizon and never test the reservoir. Perhaps the geoscientists who generated the profile shown in Figure 10-25a believed that a seismic time profile is a geological profile. Time profiles distort geometry, and the distortion increases with increasing bed dip (Chapter 5).

Figure 10-26 As most post-depositional folds are constant-thickness folds and obey the kink method, wells spudded on the crests of asymmetric folds will typically intersect steeply dipping beds within the front limbs of these folds. On asymmetric folds, wells spudded on the back limbs are more likely to discover hydrocarbons. This cross section was generated using the kink method, and thus the axial surface bisects the fold limbs. (Modified from Tearpock et al. 1994.)
Notice on the profile shown in Figure 10-25b that if the well were drilled deeper, it might have crossed the axial surface and entered the front limb of the structure. When drilling asymmetric folds, there is always the risk of crossing the axial surface that separates the gently dipping back limb from the steeply dipping front limb. If the front limb of the fold is slightly overturned, then beneath the axial surface, the stratigraphic units penetrated by a well will become younger with increasing depth (Fig. 10-44). Drilling the syncline in front of the fold is also possible when attempting to exploit asymmetric folds. The fault propagation fold is the second-most common type of fold in fold-thrust belts, so interpreters should be aware of the pitfalls associated with asymmetric folding (Tearpock et al. 1994).
The profile shown in Figure 10-25b illustrates the kink law. The kink law states that if the beds do not change thickness, then the axial surface bisects the limbs of the fold. In other words, on constant-thickness folds, the angles between the two fold limbs and the axial surface are about equal, or γ1 = γ2, as in Figure 10-26. Most petroleum-related folds come close to obeying a constant-thickness relationship and the kink law (Tearpock et al. 1994). At the correct well position, shown on Figure 10-26, the well was positioned so that it did not cross the axial surface at the reservoir level. This well intersects the reservoir horizon, whereas the dry hole (Fig. 10-25a) crosses the axial surface (Fig. 10-26). A well that crosses an axial surface can even penetrate vertically dipping or overturned beds.
Figure 10-27 is redrawn from Figure 10-25a to demonstrate that the angles between the two fold limbs and the axial surface are not equal, or γ1 is not equal to γ2. This is an indication that the fold was constructed as a thin-limb fold, and therefore the front limb may be incorrectly located. On the other hand, if the fold is actually a constant-thickness fold, then the well will cross the axial surface and penetrate the steeply dipping beds in the front limb of the fold, as shown in Figure 10-26.

Figure 10-27 On a thin-limb fold, the axial surface does not bisect the limbs of the structure. This geometry contrasts with Figure 10-26 in which the axial surface bisects the fold limbs. (Modified from Tearpock et al. 1994.)
The kink law is a powerful tool when constructing cross sections. Remember to construct the cross section on a scale of one to one. To apply the method, simply bisect the angle between the fold limbs. These procedures eliminate geometric distortions and provide a clearer picture of the complex relationships concerning folded structures.
As a final exercise, examine the three profiles of folded structures from three different fold-thrust belts in Asia, shown in Figure 10-28. Seismic and surface dip data constrain the profiles. Using the kink law, can you recognize which one of the three wells was drilled on structure, and why? Remember to bisect the angle between the fold limbs. The kink method is easy to use and rapid to apply, and it often generates cross sections that accurately predict wellbore results. The method deteriorates if the projection crosses a large fault. The method assumes that the bed dips remain about constant within each dip domain. However, bed dip may change significantly where crossing large faults and thus violate the constant bed dip assumption. The target depths of the three wells are between 1500 ft and 3500 ft, and the cross sections are drawn at a scale of one to one.
Figure 10-28 (a)–(c) Cross sections of three structures constrained by surface dip and seismic data of varying qualities. Using the kink method, can you predict which one of the three wells discovered hydrocarbons and which wells encountered steeply dipping beds? (From Bischke 1994a. Published by permission of the Houston Geological Society.)
Figure 10-28a shows a well spudded into the front limb of a symmetric monoclinal-type fold. A high-quality seismic line crosses the fold that images a steeply dipping west limb, a flat crestal area, and a more gently dipping east limb. Surface bed dips exist to aid the interpretation. Were high or low bed dips encountered in the well? Using the outcrop data, we know that an axial surface would bisect the angle between the 30-deg to 35-deg front limb dips and the flat crestal dips. We position the axial surface along the change in bed dips that image on the seismic profile, which results in an axial surface that dips steeply to the east (Fig. 10-29a). If seismic data do not exist, position the axial surface halfway between the surface data points. Dips exceeding 30 deg exist below and to the west of the axial surface. The kink method predicts that the well should encounter bed dips in excess of 30 deg at depths exceeding 1000 ft (Fig. 10-29a).

Figure 10-29 (a) The well crosses an axial surface at approximately the 1000-ft level to intersect 25-deg to 40-deg dipping beds. (b) The well is drilled on the crest of an asymmetric fold and encounters near-vertical beds. (c) The well is drilled into the back limb of a tightly folded structure and encounters hydrocarbons. (From Bischke 1994a. Published by permission of the Houston Geological Society.)
Data from the well, shown in Figure 10-29a, confirm the accuracy of the kink method. At a depth of 1200 ft, tadpole dips on the dipmeter log range between 25 deg and 40 deg. The well encountered a sand horizon below 3000 ft that requires more than a 500-ft hydrocarbon column for a discovery in this well. Notice that if a well were positioned on the back limb of the structure, near sp 700, then a smaller hydrocarbon column in that sandstone nevertheless would result in a discovery. Thus, wells spudded at the back of structures are more likely to encounter hydrocarbons than wells spudded on the front of structures. Old-timers learned this rule after drilling numerous wells. Furthermore, wells drilled into the back-limb axial surface not only are more likely to encounter hydrocarbons but are commonly the most productive wells. We return to this empirical observation and suggest a cause for the increased production in this chapter’s section on the kinematics of fault bend folds.
Next, examine Figure 10-28b, which contains a well spudded into an asymmetric fold at the crest of structure. This fold, constrained by surface bed dips, exhibits a near-vertical front limb. Seismic data do not image these steep bed dips. Applying the kink method to the surface bed dips results in the interpretation shown in Figure 10-29b. The kink method predicts that the well should encounter near-vertical bed dips below 1000 ft. Tadpole dips obtained from dipmeter data below 1000 ft confirm the accuracy of the kink method prediction. The kink method solution suggests that a well spudded between sp 250 and sp 300 would encounter the sand horizon at a depth of 1200 ft.
Last, examine Figure 10-28c, constrained by surface bed dips and poor-quality seismic data. The interpreters who drilled this well used the kink method to constrain the interpretation. The well was spudded off the crest of structure on the more gently dipping back limb. Dipmeter data confirms the interpreted dip. This well resulted in a hydrocarbon discovery and appears to intersect the subsurface crest of the reservoir horizon (Fig. 10-29c).
We have used the recognition of axial surfaces on seismic data and applied them to fold interpretation. When interpreting seismic data, you must always be aware of the probable existence of axial surfaces. Seismic interpreters commonly mistake axial surfaces for faults because of the abrupt changes in dip. You can avoid that mistake if you understand the geometry of the possible structures in the area and follow some of the common-sense methodology discussed.
In conclusion, the kink method is relatively easy to use and makes accurate predictions when applied to depth-corrected seismic data and outcrop bed dip data. If the kink projection method does not cross a large fault, then the method typically generates accurate cross sections of subsurface geometry. Bed dips can change across large faults, causing the solution to deteriorate. Remember that surface bed dip data are some of the cheapest data available to interpreters. When employing 2D seismic data, collect the bed dip data along and adjacent to the seismic survey lines. On well-constrained structures, the method typically generates accurate results (Suppe and Medwedeff 1990).
Structures typically contain steeper dipping frontal limbs relative to gentler dipping back limbs. Wells positioned on the back limb of symmetric and asymmetric structures increase the odds of encountering hydrocarbons. On the other hand, wells spudded near the steeply dipping frontal limbs of structures often encounter steep bed dips. If the well penetrates the overturned limb of an asymmetric fold, then the beds will become younger as the well deepens, potentially missing the prospective horizons.
Tearpock et al. (1994) discuss additional pitfalls concerning fault propagation folds and other complex structure styles. A strong structural geological background is key to exploring in these areas. The understanding of compressional structural styles, including the types of faults and folds and their inseparable relationship, is paramount when exploring in fold-thrust belts (Bischke 1994a).
Depth-to-Detachment Calculations
A method to determine the depth at which folding terminates can be attributed to Chamberlin (1910) and to Bucher (1933), who applied the method to determine the depth to detachment in the Jura Mountains. If the sequence that you are studying consists of a number of folds, then each fold must be isolated and studied separately. In this method, you measure the length (lo) of a marker or reference bed, the present pin length (l), and the average amount that the marker bed has been uplifted (Ū) above the undeformed level of the bed, as shown in Figure 10-30. The average uplift (Ū) is calculated using the same methods engineers use to calculate reserves (Fig. 10-30). The amount of shortening (S) that the unit has experienced is defined as

Figure 10-30 The average amount that a marker bed has been uplifted can be determined by measuring equally spaced line segments that are drawn between a base level and the marker bed and then averaging the line lengths.
The average amount of uplift times the present length (Ū) equals the average area of uplift, which is then equated to the amount of material that enters the structure from the sides (S × d), where d is the depth to detachment (Fig. 10-31).
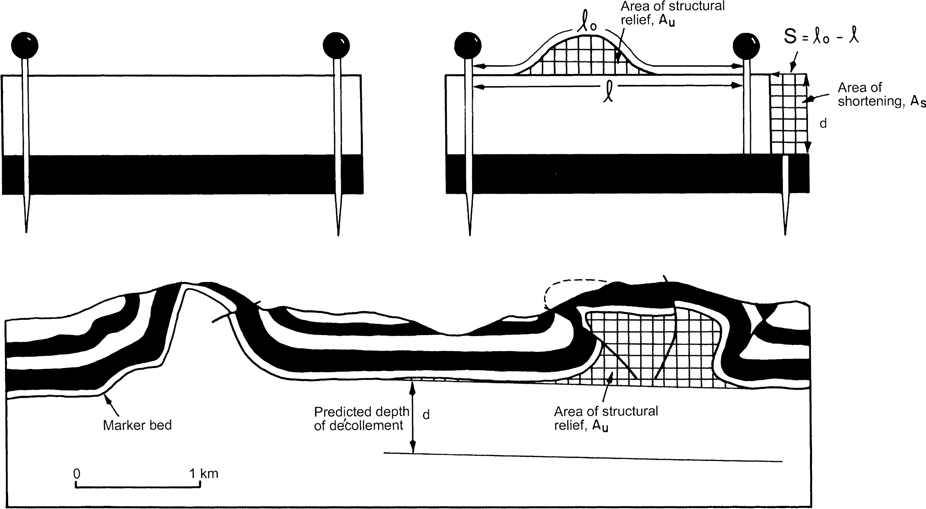
Figure 10-31 Depth-to-detachment calculation. The amount of material entering the cross section from the sides is equal to the material that has been uplifted above base level. (Modified after Laubscher 1961; Suppe 1985. Published by permission of the Swiss Geological Society.)
It therefore follows (Bucher 1933) that
Alternatively, if the depth to detachment is known, then the method can be used to check fold shape.
A closely related method employed by Laubscher (1961) and described by Goguel (1962) has been used in the petroleum industry. This method also assumes that no material is entering the structure from below, as in a duplex (see the section on duplex structures), and that all the material in the core of the structure is derived from the sides of the structure. Mitra and Namson (1989) point out that these assumptions are invalid if there is interbed shear (i.e., distortion of the vertical pin line) or if material is transferred out of the area of the cross section, as occurs in fault bend folds.
If the material enters the structure from the sides, then the area within the core of a structure (Au) at a given reference level is measured, as are the final pin length (l) and the initial length (lo) of a reference or marker bed (Fig. 10-31). As before, the shortening at the reference level is
The area (Au) within the core of the structure beneath the reference bed is assumed to be equal to an equivalent volume that comes in from the side (As) (Fig. 10-31). The area can be obtained by planimetry.
Therefore,
where d = depth to detachment, and as
it follows that
and
Nonclassical Methods
Introduction
Newer methods of structural interpretation are more precise and more robust than the classical balancing techniques, which have distinct limitations. For example, Dahlstrom (1969) emphasized that within a given area, only a limited number of geological structures are likely to exist. He also realized that these structures must area-balance and line-length balance, but exactly how does the interpreter accomplish these tasks? One obvious method is to measure formation bed lengths to check for balance, but this can only be accomplished after the interpretation is finished. In addition, two geoscientists given the same data set are very likely to place lines of equal length at different positions within a cross section, although both products may be line-length balanced sections! How are we to evaluate which of the two sections is “correct,” and how could the interpretations be improved? One problem is that line-length balancing has no rules associated with the method, other than that the bed lengths must be consistent and that the structural styles are limited.
This problem becomes particularly acute when the data in an area are under-constrained, as is often the case and leads to what John Suppe has referred to as the “blank paper” problem (Woodward et al. 1985). For example, you are studying an area in which the only data available are at shallow depths, and these data strongly suggest that the structures continue with depth. Classical balancing lacks constraints, so any attempt to continue the interpretation to depth is likely to result in as many interpretations as there are interpreters. Furthermore, line-length balance can be conducted only after an interpretation is finished. Do methods exist to more directly balance a section, either by hand or with the use of a workstation? More direct methods would certainly be friendlier to the working environment.
Those of you who have worked with various tectonic settings know that several relationships are recurrent from area to area. In extensional terranes, the faults are commonly listric and rollover structures are present, which typically contain antithetic and synthetic minor faults and perhaps a keystone structure. This suggests that some fundamental process controls the development and formation of normal faults and associated structures. In the compressional regime, folds are either symmetric, as described by Gwinn (1964) in his work on the Appalachians, or they are asymmetric, such as many of the folds in the Rocky Mountains (Link 1949). Geologists have noticed that where folds are present, faults also seem to exist in association with the folding (Bally et al. 1966; Jones 1971; Woodward et al. 1985). Many different regions around the world possess thrust belts that contain within them symmetric and asymmetric folds, so fundamental processes seem to control the formation of orogenic belts. If we could develop realistic models of these fold-and-thrust belt folds, then the petroleum industry would have powerful tools in which to aid interpretation.
In the section Kink Method Applications, we presented three examples of how surface dip data could reflect symmetric or asymmetric styles (Fig. 10-29). In particular, the surface dips could reflect off-structure problems and the resulting pitfalls. For this reason, we have added Determining Structural Styles to Reduce Risk Using Qualitative and Quantitative Techniques, a section based on recent research presented in this chapter. This section uses measurements of the displacements on thrust faults, throw, structural relief, and repeated section to quantify structural styles. Several mathematical formulas are developed to quantify the process and to check interpretations for structural validity.
Hence, we enter the world of nonclassical methods that utilize mathematical formulas, graphs, and models. Perhaps a word of caution is required at this time for the new geology student. Although models can be very powerful tools (e.g., the plate tectonic model), the improper application of a correct model to the wrong situation will only result in error. To make matters worse, model balancing is nonunique. Different geoscientists, applying the same model to a given structure, are likely to generate similar results, as we shall see. However, the skeptic may point out that this is merely an artifact of being schooled in the same interpretation techniques.
Before we enter the exciting world of kinematic processes, we restate that this book is designed primarily to present subsurface mapping techniques and is not a complete reference on interpretation per se. In the balancing sections of this book, the mapping techniques are commonly difficult to separate from the interpretation because you must choose which technique to apply to a given structure, and this choice involves interpretation. Let us caution you that other interpretation techniques exist that do not involve any particular mapping technique, such as growth sedimentary patterns and structures (Medwedeff and Suppe 1986). These growth patterns are often extremely helpful in determining which model or technique to apply to the structure, so we recommend that the serious geoscientist gain familiarity with all the approaches to structural interpretation.
Suppe’s Assumptions and Dahlstrom’s Rules
When presented with the problem of a poor or nonexistent data set, several approaches are open to the geoscientist. Solutions to this problem seem to involve the following.
Collect more and/or better data. This subject is left to the data contractors.
Make more assumptions in order to solve the structural problem. If data are lacking or are unobtainable, it is still possible to solve the structural problem, providing you can extrapolate known data, using known geological principles, into the area of interest. For example, if we assume that the kink method is appropriate, we can extrapolate units within the limb of a fold to depths beyond the control data. In this sense, assumptions can substitute for data.
We recommend that you employ the following assumptions and rules credited to Suppe (1988) and Dahlstrom (1970).
Suppe’s Assumptions
Thrust faults step up abruptly from a decollement and (unless deformed) do not have continuously curved listric shapes.
All thrust faults (that produce a given structural style) in a given area step up at approximately the same angle.
Layer-parallel slip in a thrust sheet is limited to that caused by changes in dip. This is another way of stating that the kink method applies at all times.
Dahlstrom’s Rules
Dipping beds over flatter beds define decollements or thrust faults (Fig. 10-5c).
Thrust faults cut up, and not down, stratigraphic section.
Invent more powerful interpretation methods and techniques so that you can extrapolate existing data into the no-data areas. This is the subject of the remaining sections in this chapter.
Fault Bend Folds
Our examination of seismic sections from various areas of the world (Australia and through the Pacific rim to Alaska, western and eastern United States, western Europe, Argentina, Venezuela, etc.) indicate that there are two commonly recurring fold styles within the low-temperature portions of thrust belts: the symmetric, or fault bend fold type (Figs. 10-32a and b and 10-34) (Rich 1934; Suppe 1983) and the asymmetric, or fault propagation fold type (Fig. 10-42) (Link 1949; Suppe 1985). The simplest, end-member structural styles are shown in Figures 10-34 and 10-37 for fault bend folds and in Figure 10-43 for fault propagation folds. See Figure 10-33 for the front planal of a fault bend fold. We stress here that complications in these structures, such as multiple and back thrusts, often exist and that other thrust-related geometries are present (Fig. 10-34). For a more complete discussion of variations in structural style, consult Suppe (1983), Suppe and Medwedeff (1990), and Shaw et al. (2005). We wish to emphasize, however, that these two structural styles are the simplest types of compressional folds that are commonly present in petroleum basins. Fault bend folds appear to be the most common of the two structural styles, and a case history of the El Furrial Fault-Bend Fold Trend is presented in the next paragraph. Also, in the section on Quantitative Methods for Determining Structural Styles is a discussion on qualitative and quantitative methods to determine the two major structural styles.
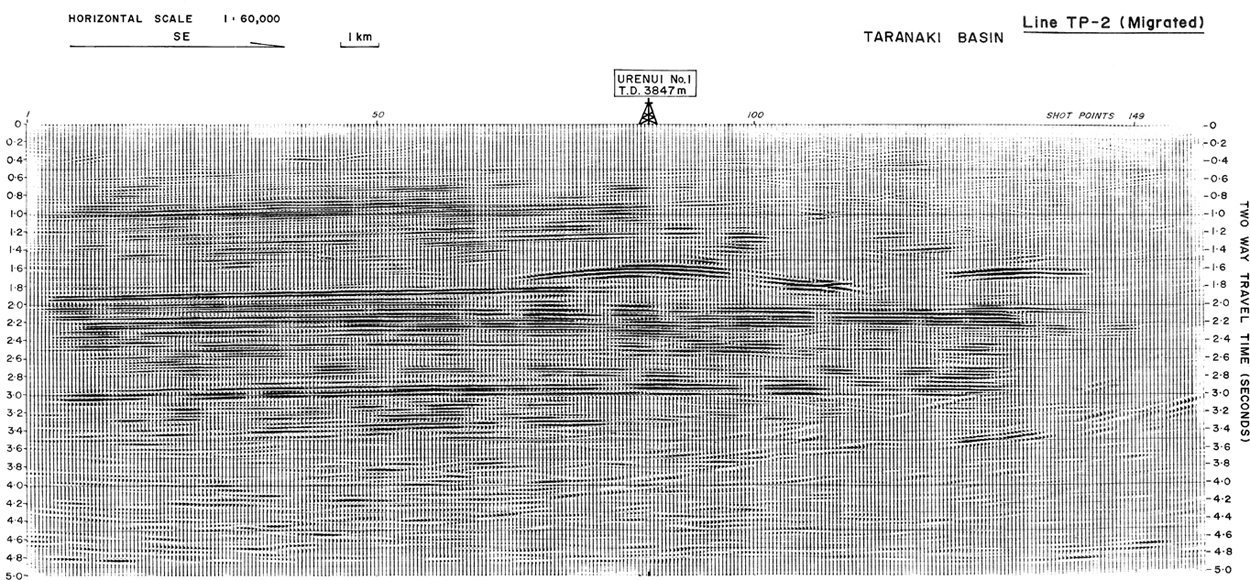
Figure 10-32 (a) Migrated 2D seismic line of fault bend fold from the Taranaki Basin, New Zealand. A symmetric fold is imaged in the vicinity of the well and sp 100, between the two-way travel times at 1.5 sec to 1.9 sec. In the vicinity of sp 75 and sp 100, dipping beds overlie flat beds, indicating a decollement. (From Seismic Atlas of Australian and New Zealand Basins, Skilbeck and Lennox 1984. Published by permission of Earth Resources Foundation, University of Sydney.) (b) For a color 3D fault bend fold example from the El Furrial Field, Monagas Venezuela, see Figure 10-51. (Reprinted by permission of the AAPG whose permission is required for further use.)

Figure 10-33 Frontal limb of a fault bend fold in Hudson Valley, New York, USA, located on Route 23 about 300 meters west of the New York State Thruway. (Compliments of Jon Mosar.)
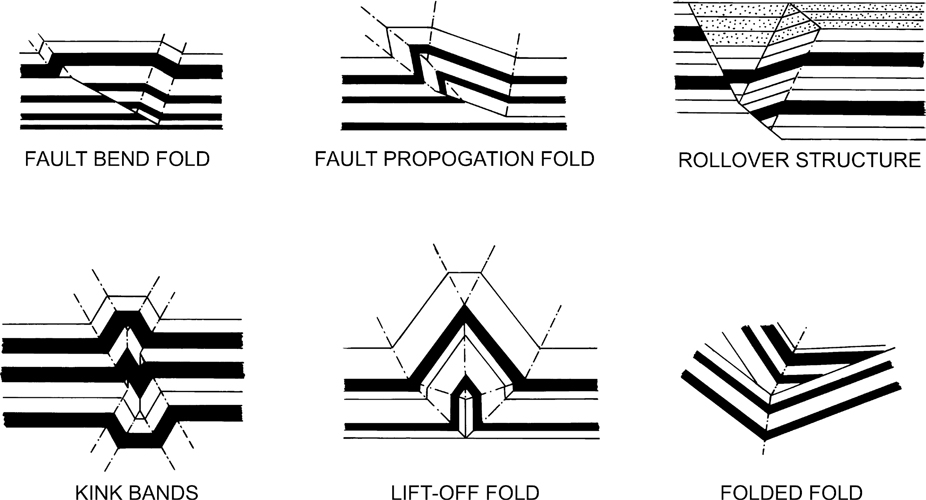
Figure 10-34 Examples of fault-related fold types. (Published by permission of John Suppe.)
The following paragraphs present a short case history of the El Furrial Fault-Bend Fold Trend (Fig. 10-51a and b). Fault bend folds and their related structures (see shear fold example in Fig. 10-53), are some of the world’s largest producers. Some of the examples that we are familiar with include fault bend style folds in the deep-water Nigeria, such as the Agbami Field, which has reserves reported in excess of 2.0 billion barrels of oil. Another example, this one in the United States, is the line-length balanced Whitney Canyon cross sections associated with the Absaroka fault presented by Lamerson (1982).
A good color 3D seismic example is the El Furrial Fault-Bend Fold, north Monagas, Venezuela, which is a balanced structure (Morales et al. 2005) (Fig. 10-51a) similar to Figure 10-43. Three fault bend folds lie along this trend for 45 km (28 mi), although some of the structures are imbricated. From east to west, these fields consist of the El Furrial, Carito, and Tejero/Santa Barbara structures, that contain about 11 billion barrels of oil in place (Morales et al. 2005). The interpreted and depth-corrected sections shown in Figures 10-51a and b are area-balanced sections generated from software. Figure 10-51b is a strike line that crosses the dip line (Fig. 10-51a) along the vertical dashed line “B” on the front limb of the structure. The orange horizon at the high-impedance contrast is the productive Naricual sands that are about 500 m (16,000 ft) thick.
The El Furrial fault is at a depth of about 5.7 km and repeats about 3.5 km of Naricual section from the crest of structure. Following Dahlstrom’s rule 1 from the previous section, that the fault exists where dipping reflections terminate against flatter dipping reflections, we interpret that the fault on Figure 10-51a lies above the black line at the horizontal, high-impedance reflection (the black line is positioned lower so as not to cover the high-impedance contrast). This dipping-over-flat relationship for picking faults is more obvious on the dip line in Figure 10-51a, to the right of vertical line “B,” which defines where the strike line crosses the dip line. At this location, the dipping hanging wall reflections terminate against a very bold flat reflection. This bold, flat refection, at about 5.7 km, is caused by a strong impedance contrast caused by over-thrusting denser and higher-velocity rocks over less dense and lower-velocity rocks. Again, the fault is located at the top of the bold reflection, but was placed below the high-impedance contrast in order not to cover the seismic data.
Fault bend folds were first described by Rich (1934) in the Pine Mountain thrust region of the Appalachians, where he recognized that this fold style consisted of symmetric anticlines (Fig. 10-35). Rich also recognized that these folds were associated with thrust faults, and he postulated that the folds were the result of thin-skinned deformation. Notice that if motion were to occur along the decollement in Figure 10-2, hanging wall material would ride up the ramp and onto the flat. Rich recognized that if this occurs, anticlines and synclines would form (Fig. 10-36). This example was eventually modeled utilizing a mathematical volume conservation concept (Suppe and Namson 1979; Suppe 1980, 1983).
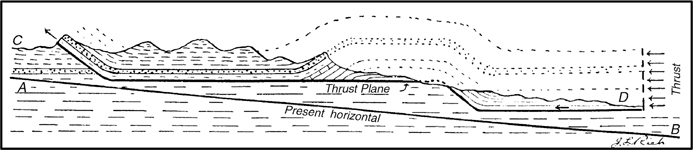
Figure 10-35 Fault bend fold forming over a step-up on a thrust fault. (From Rich 1934. AAPG©1934, reprinted by permission of the AAPG whose permission is required for further use.)

Figure 10-36 Model of fault bend fold constructed from paper sheets. (From Rich 1934. AAPG©19341934, reprinted by permission of the AAPG whose permission is required for further use.)
Often, interpreters rely solely on computer-generated solutions without understanding how the software program’s algorithms actually work or whether the computer-generated solution to a problem is reasonable. We have seen cases where overreliance on software can result in very costly mistakes. The following sections on resolving the geometry of fault bend folds, fault propagation folds, and imbricate structures are presented (1) to give the interpreter a better understanding of, and intuition about, the results from balancing software; and (2) to illustrate what a geometrically reasonable computer-generated area-balanced solution looks like.
The kinematics of the simplified fault bend fold modeling process are as follows. Folds form along nonplanar thrust faults where a decollement on a lower structural level (Y level, Fig. 10-37a) ramps to a higher stratigraphic level (X level) (Rich 1934; Bally et al. 1966). Motion along the fault and the conservation of volume principle cause the beds to ride up the ramp and roll through axial surface BY, forming the back limb of the anticline. This causes the back dip panel (or flap) BYY′ B′ to form (Fig. 10-37a). The two axial surfaces (BY and B′Y′) terminate at the fault surface, because they are produced by the bend in the decollement as the beds move up the ramp. Axial surface B′Y′, which is pinned to the bend in the fault, is actively deforming the hanging wall beds. The bend in the fault causes the deformation. Axial surface B′Y′, which was initially at the BY position, passively moves up the ramp as material moves through the bend in the fault. Similarly, the beds moving up the ramp and onto the flat must roll through axial surface AX, forming the frontal dip panel AXX′A′ (Fig. 10-37a). Axial surface AX, which is also pinned to a bend in the fault, is a locus of active deformation and rotation of the hanging wall beds. The beds roll down at axial surface AX and form the front limb of the anticline. As the beds roll through axial surface AX, they experience bedding plane slip. This slip produces shear in the frontal limb of the fold (Fig. 10-37b) and causes the frontal limb to dip at a higher angle than the back dip panel. This point is emphasized here because it will be applied to the solution of more complicated problems in the section on duplexes. As the beds roll through the active axial surfaces BY and AX, a fracture porosity is likely to form in the deformed beds. Some of the best producing wells drilled on anticlines produce from rocks close to the active axial surface B′X′, shown in Figure 10-37c. Bending of the strata along this active surface apparently imparts an excellent permeability in some folds.
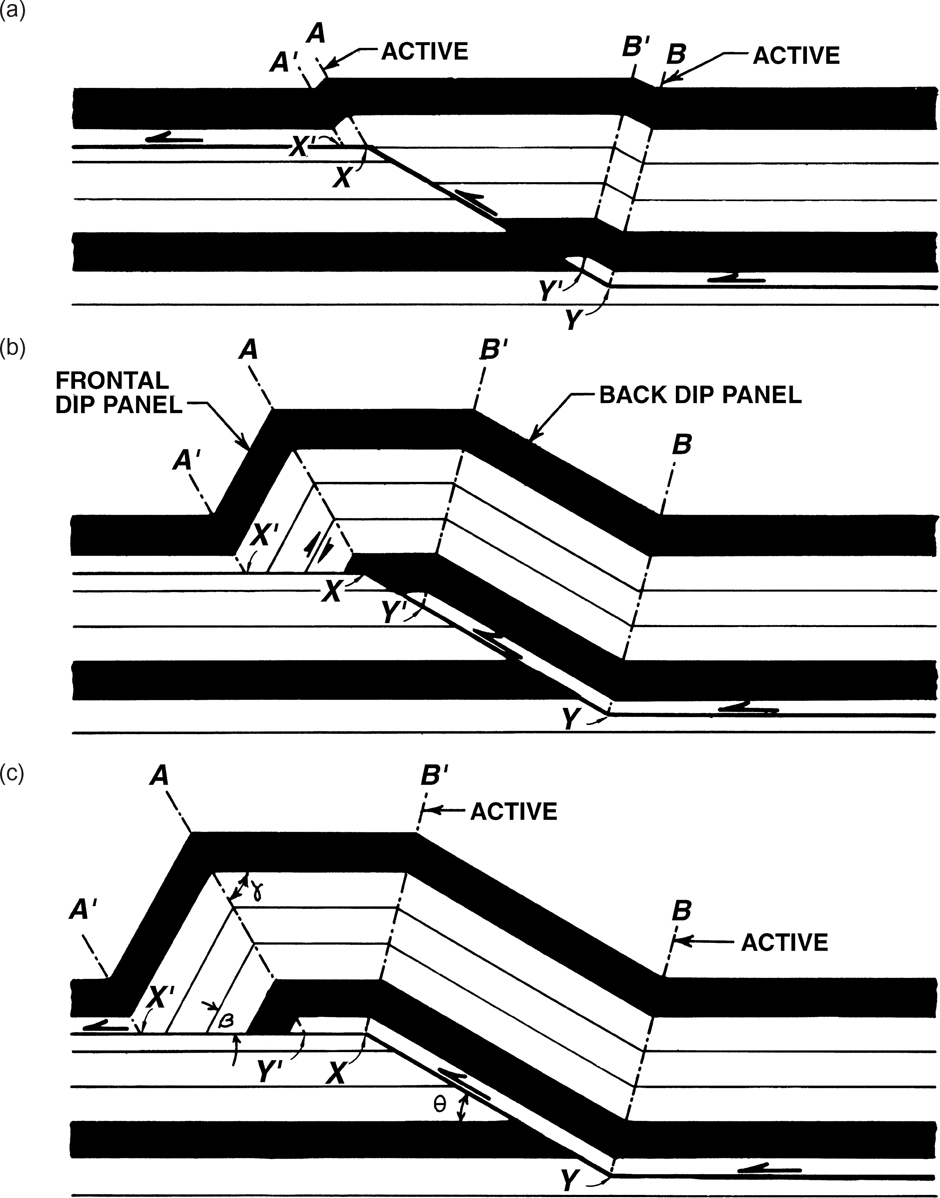
Figure 10-37 Fault bend fold kinematics illustrating the progressive development of beds riding up a thrust ramp. The beds are deformed by the active axial surfaces. (Modified after Suppe 1983, 1985. Published by permission of the American Journal of Science.)
As fault slip increases and the fold grows, the dip panels extend in width, and point Y′ migrates toward point X (Fig. 10-37b) until the fold attains its maximum amplitude. When this occurs, axial surface B′Y′ has migrated to the top of the ramp and point Y′ has reached the upper footwall cutoff (point X in Fig. 10-37b). With additional deformation, the fold now extends by the lateral motion of axial surface AY′ away from axial surface B′X (Fig. 10-37c). The fold has reached its maximum amplitude and now is only widening, so no material is currently rolling through the AY′ axial surface. This surface has become inactive. However, material continues to roll through the B′X and BY surfaces, probably further fracturing the rock.
The resulting idealized fold shape, caused by simple step-up of the hanging wall material along a ramp and onto a flat, has a frontal dip panel that contains a slightly higher dip than the back dip panel (β is usually slightly greater than θ, as in Fig. 10-37c). Thus, the fold geometry is roughly symmetric, particularly at cutoff angles (θ) of less than about 20 deg.
The mathematics of this volume-balanced model can be summarized in the form of a graph (Fig. 10-38). This model vigorously utilizes the kink method, and as this method conserves volume, line length, and bed thickness, it is not necessary to retrodeform a solution that is derived from Figure 10-38. If the data conform to the angles presented in Figure 10-38, the interpretation will automatically retrodeform. Thus, the graphical methods presented in this section are useful in both exploration and exploitation activities.

Figure 10-38 Fault bend fold graph showing angular relationships between the initial cutoff angle (θ), the frontal dip panel (β), and the axial surface angle (γ). (From Suppe 1983. Published by permission of the American Journal of Science.)
Let us apply Figure 10-38 to the case of a fault that steps off a decollement at a 20 deg (initial) cutoff angle and ramps to an upper flat that parallels the lower decollement (Fig. 10-39a). This means that ϕ = θ (Fig. 10-38, insert on left). Also, notice that when ϕ = θ, θ cannot exceed 30 deg (see Fig. 10-38). The other assumption that we shall make for purposes of demonstration is that the amount of slip on the lower decollement is equal to the ramp length. This means that the axial surface (B′Y′ in Fig. 10-39b) has moved up to the top of the ramp. The initial cutoff angle of 20 deg can now be read off the left part of the abscissa and projected vertically on Figure 10-38 until this line intersects the θ = ϕ line. Next, the dip of the front flap (β) can be read off the more steeply dipping lines on Figure 10-37, which in this case is about 23 deg (also see Table 10-1). The axial surface angle (γ) can be read off the ordinate, which in this case is 78.5 deg. The final solution, shown in Figure 10-39b, will automatically area-balance and line-length balance, but there is a final check that should be made.
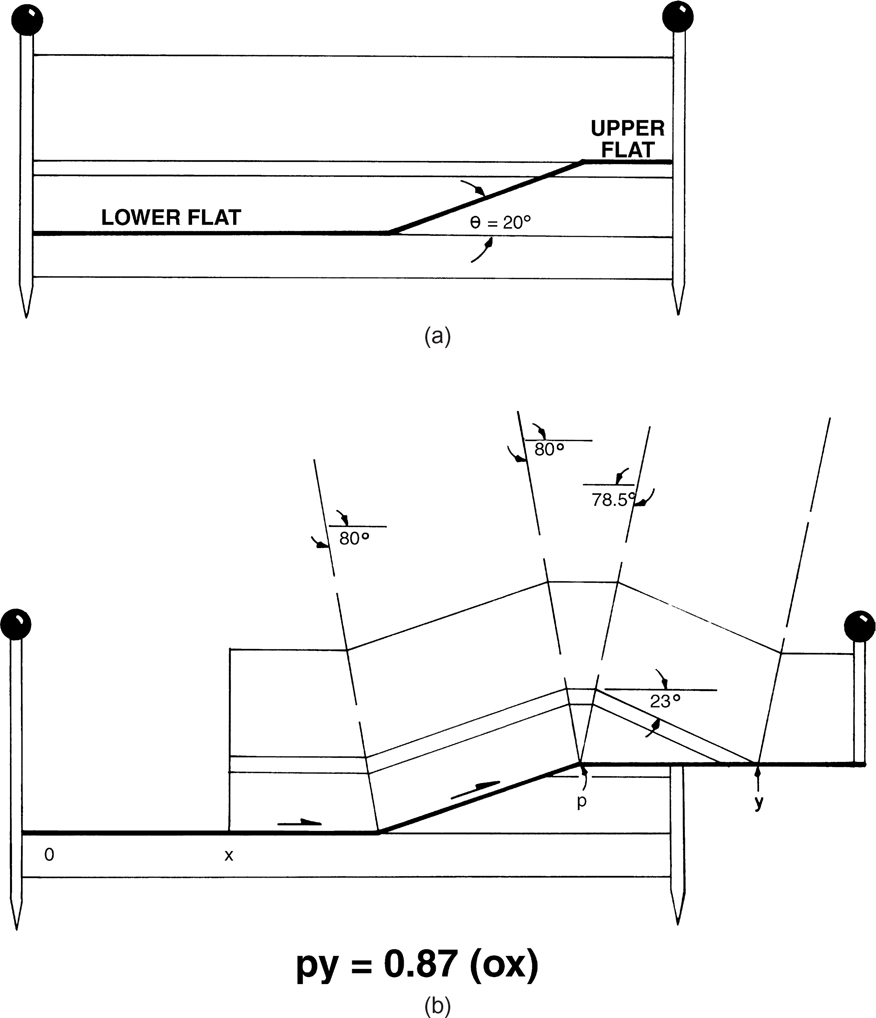
Figure 10-39 Fault bend fold exercise for beds ramping up a fault with a 20-deg cutoff angle and with slip on the lower decollement equal to the ramp length.
Table 10-1 Dip Spectral Analysis
Forward dips (+) |
Fundamental cutoff angle θ |
Back dips (—) |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
VII |
VI |
V |
IV |
III |
II |
I |
I |
II |
III |
IV |
V |
VI |
VII |
|
61.6° |
52.5° |
43.0° |
34.0° |
25.2° |
16.6° |
8.2° |
8° |
8° |
15.9° |
23.4° |
30.6° |
37.3° |
43.5° |
49.3° |
70.2° |
59.2° |
48.6° |
38.3° |
28.3° |
18.6° |
9.2° |
9° |
9° |
17.8° |
26.2° |
34.0° |
41.3° |
47.9° |
53.9° |
80.6° |
67.6° |
55.2° |
43.3° |
31.9° |
20.9° |
10.3° |
10° |
10° |
19.7° |
28.9° |
37.4° |
45.1° |
52.0° |
58.2° |
93.1° |
77.3° |
62.6° |
48.8° |
35.7° |
23.3° |
11.4° |
11° |
11° |
21.6° |
31.5° |
40.6° |
48.7° |
55.9° |
62.2° |
109° |
88.8° |
71.0° |
54.8° |
39.8° |
25.8° |
12.6° |
12° |
12° |
23.5° |
34.1° |
43.7° |
52.1° |
59.5° |
65.9° |
128° |
102° |
80.5° |
61.5° |
44.3° |
28.5° |
13.8° |
13° |
13° |
25.4° |
36.7° |
46.7° |
55.4° |
62.9° |
69.4° |
160° |
119° |
91.3° |
68.6° |
48.9° |
31.2° |
15.0° |
14° |
14° |
27.2° |
39.1° |
49.5° |
58.4° |
66.1° |
72.5° |
— |
146° |
104° |
76.3° |
53.6° |
33.9° |
16.2° |
15° |
15° |
29.1° |
41.5° |
52.3° |
61.4° |
69.0° |
75.5° |
— |
124° |
85.9° |
59.0° |
36.8° |
17.4° |
16° |
16° |
30.9° |
43.9° |
54.9° |
64.1° |
— |
||
— |
99.2° |
65.6° |
40.2° |
18.8° |
17° |
17° |
32.7° |
46.2° |
57.5° |
— |
||||
— |
123° |
73.1° |
43.7° |
20.2° |
18° |
18° |
34.4° |
48.4° |
59.9° |
— |
||||
— |
82.2° |
47.4° |
21.6° |
19° |
19° |
36.2° |
50.6° |
— |
||||||
— |
97.6° |
52.0° |
23.2° |
20° |
20° |
37.9° |
52.7° |
— |
||||||
— |
57.0° |
24.8° |
21° |
21° |
39.6° |
— |
||||||||
— |
63.6° |
26.6° |
22° |
22° |
41.3° |
— |
||||||||
— |
72.0° |
28.4° |
23° |
23° |
42.9° |
— |
||||||||
— |
30.4° |
24° |
24° |
— |
||||||||||
Published by permission of the American Journal of Science (Suppe 1983).
The amount of slip on the upper flat is less than that on the lower flat. Previously, we stated that as the beds rolled through axial surface AX (Fig. 10-37a), the deformation was accommodated by bedding plane slip within the frontal dip panel. This is required to conserve both volume and bed thickness, and it causes angle β to be larger than angle θ. Thus, some of the fault slip is consumed within the beds of the frontal dip panel, and that causes the amount of slip along the upper flat to be less than the amount of slip along the lower flat.
The amount of slip to be expected along the upper flat can be determined by using Figure 10-40. Again, a vertical line is projected from the 20-deg cutoff angle on the left part of the abscissa vertically upward to the θ = ϕ line that we have assumed for this example. The ratio of the slip on the upper flat relative to the slip on the lower flat can now be read from the R lines on the diagram, which in this case is about 0.87. Therefore, the slip along the upper flat must be 0.87 of the slip along the lower flat. Field geologists have often observed that the slip on faults dies or decreases within the cores of folds, and this is one reason why fold belts die toward the foreland. This exercise for checking slip is most useful when experimenting with structures that exhibit unusual geometries or complicated shapes. Another check on the solution would be to measure bed lengths on more than one structural level.
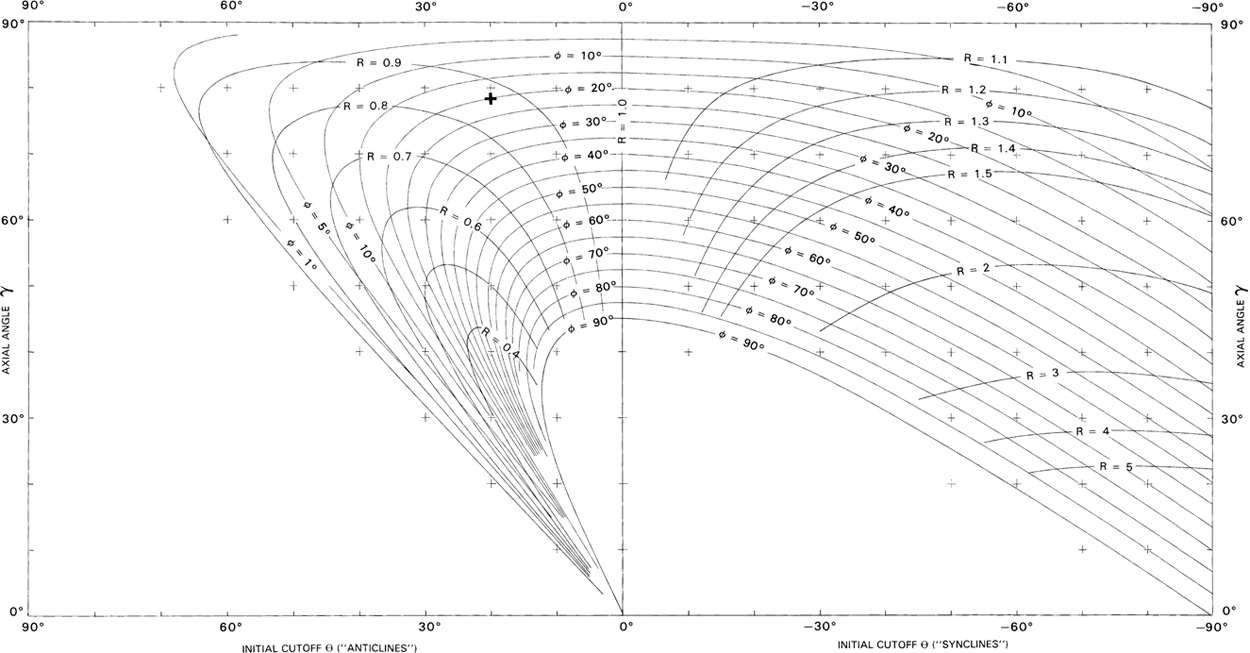
Figure 10-40 Fault bend fold graph showing the amount of slip to be expected along different portions of a fault surface. The R lines indicate the ratio of slip along the upper flat relative to slip along the lower flat. (From Suppe 1983. Published by permission of the American Journal of Science.)
We can now present a major conclusion concerning fold geometry. Perhaps you have noticed the relationship between fault shape and fold shape. The shape of the fault is related to the shape of the fold (Rich 1934; Dahlstrom 1969) and indeed, fault shape determines fold shape (Fig. 10-36). Thus, if you know fault shape, you can predict fold shape, and conversely, if you know fold shape, you can infer something about fault shape. For example, on Figure 10-37b and c, notice how the thrust ramps up where the fault flat intersects the synclinal axial surface BY. So, as the fault ramp parallels the back limb of the upturned hanging wall beds. The location where the thrust intersects the active axial surfaces AX or B′X, the thrust forms the upper flat.
Fault Propagation Folds
Fault propagation folds are a common fold type observed in outcrop and on seismic data (Figs. 10-41 and 10-42), and like fault bend folds, they are known to be good hydrocarbon producers. Fault propagation folds possess the particular characteristic that as the fold grows, the deformation advances at the tip of a propagating thrust fault (Fig. 10-43), hence the name “fault propagation fold” (Suppe 1985). As long as the structure has not been faulted through (i.e., been subject to breakthrough), the slip is consumed by bedding plane slip within the frontal limb of the fold (Fig. 10-43c).

Figure 10-41 (a) Two-dimensional seismic section imaging asymmetric fault propagation folds, Southern Appalachians, Alabama. (Interpretation by R. Bischke. After Sachnik and More in Bally 1983 AAPG©1983, reprinted by permission of the APPG whose permission is required for further use.) (b) A 3D seismic example of a fault propagation fold from Northern Apennines, Italy (Storti et al. 2005. Reprinted by permission of the AAPG whose permission is required for further use.)

Figure 10-42 Fault propagation fold, Appalachians, Tennessee. The front limb dips more steeply than the back limb. Thrust fault dies near synclinal axial surface at the front of the fold. (From Suppe 1985.)
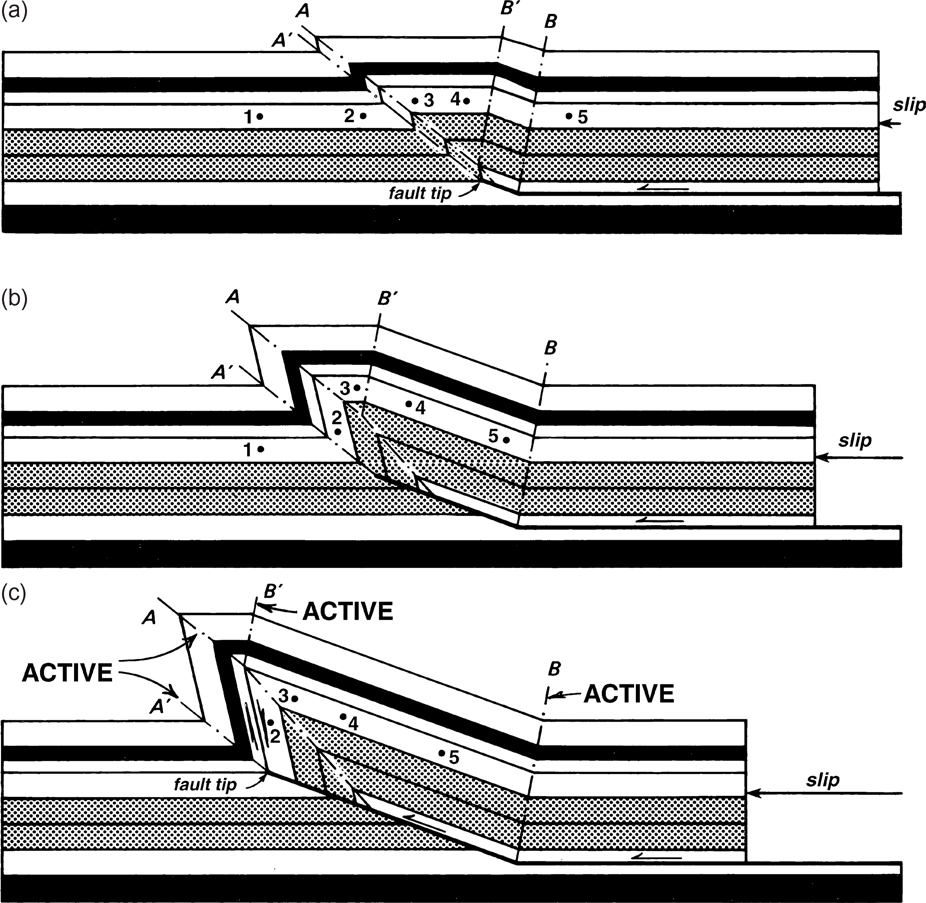
Figure 10-43 Fault propagation fold kinematics, illustrating the progressive development of beds deforming at the tip of a propagating thrust fault. (Modified after Suppe 1985.)
Fault propagation folds typically have higher cutoff angles than fault bend folds, in the range of about 20 deg to 40 deg, which causes these fold types to possess steeply dipping to overturned frontal limbs that commonly do not image on seismic sections, along with a characteristic asymmetry (Figs. 10-41 and 10-44). This striking asymmetry, where imaged on seismic sections across folds with less dip, has the appearance of a striking snake, giving rise to the expression snakehead structure (Fig. 10-41).

Figure 10-44 Fault propagation folds at different cutoff angles. Frontal limb dips increase as the cutoff angle decreases. At low cutoff angles, the frontal limb dips are too high to be imaged on conventional seismic sections. (Published by permission of John Suppe.)
The kinematics of simple fault propagation folds are as follows. Suppe and Medwedeff (1990) discuss more complex models in their paper. A fault, propagating upward from a decollement, causes beds at the front of the propagating fault tip to bend forward as material moves up the ramp (Fig. 10-43a). As in fault bend folding, the beds will also bend up the ramp created by the propagating thrust fault as they move through axial surface B, creating the back dip panel outlined by axial surfaces B and B′ (Fig. 10-43a).
In this style of folding, an increase in the amount of deformation within the core of the fold accommodates the slip on the fault. Therefore, the beds near the tip of the thrust fault bend forward, commonly at steep angles (Fig. 10-43a). The rotation of these steeply dipping beds, and bedding plane slip between the beds, consumes the slip along the thrust fault. Thus, the slip on the fault dies out within the core of the fold. This type of fault is referred to as a blind thrust. The more steeply dipping beds between the front and the top of the structure form two axial surfaces, A and A′, as shown in Figure 10-43a.
During fault propagation folding, all the axial surfaces are active and, with the exception of axial surface B, move through the material as the beds deform (Fig. 10-43). As the propagating fault extends and the fold grows in amplitude, it incorporates more material into the frontal limb of the structure. Consequently, as the fault propagates forward and as axial surface A′ moves away from axial surface A, point 2 of Figure 10-43a and b rolls through A′ into the steeply dipping frontal limb. With increasing deformation, the dip panels, as defined by axial surfaces A and A′ and by B and B′, broaden (Fig. 10-43c). Axial surface B′ is an active surface, as beds roll through it from the crest of the fold into the back limb. Axial surfaces A and B′ form a branch point at the same stratigraphic horizon as the fault tip. As the fault propagates, the loci of deformation, and thus the axial surfaces and the branch point, move forward and upward. The structurally lower beds fold more tightly, and the back limb of the fold widens. As the fold grows, the deformation also fractures the rock, which can affect the porosity and permeability.
Fault propagation folding can exhibit a variety of structural styles, depending on the cutoff angle (Fig. 10-44) and the amount of slip. As the cutoff angle increases, and for the same amount of slip, the folding will appear to be more symmetric on seismic sections even though the amount of slip remains unchanged. If the fold forms according to the processes described in Figure 10-43, the cutoff angle can be determined directly from the dip of the beds within the back dip panel, as these beds parallel the ramp.
Given additional amounts of slip, the fault propagation may find a weak or incompetent horizon that parallels bedding and becomes a hybrid fault bend fold (Fig. 10-45b, decollement breakthrough). Alternatively, the structure can break through the anticlinal, the synclinal, or the overturned limb portions of the fold, creating more complex geometries (Fig. 10-45a, c, and d).
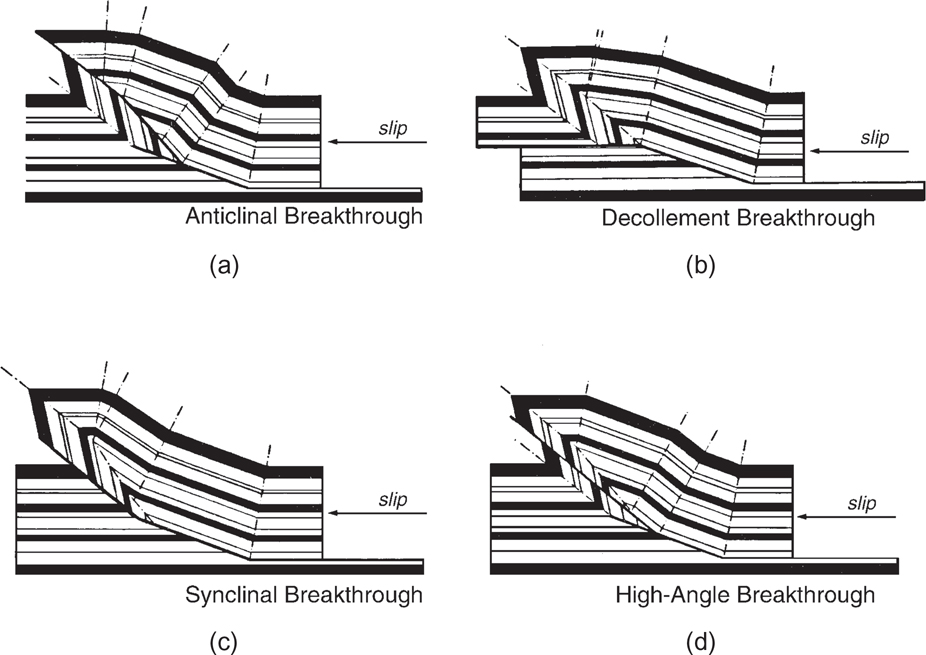
Figure 10-45 Different types of fault propagation breakthrough. (Published by permission of John Suppe.)
As with fault bend folds, fault propagation folds can be balanced using formulas or graphs, as in Figure 10-43 (Suppe 1988; Suppe and Medwedeff 1990). In outcrop or on seismic sections, simple fault propagation folds can be balanced by observing either the ramp angle (θ) or the back limb dip of the fold. When using seismic data, remember to depth-correct the seismic or choose sections that are roughly on a scale of one to one. This can be readily accomplished on the workstation over a given interval by using checkshot data or velocity information. We have found this procedure to be adequate for most cases.
We study a simple case for balancing fault propagation folds, using Figure 10-47. For example, you may observe beds on a depth-converted seismic section dipping and overlying horizontal beds. The back limb beds are determined to dip at 30 deg, so θ = 30 deg. The corresponding axial surface angles γp and γ*p can be read off Figure 10-46 (γp = 53 deg and γ*p = 38 deg). The kink method can now be employed by using Figure 10-47. (Note how angles are measured in the figure.) First, construct a 30-deg dipping ramp, with the tip of the thrust fault as best determined from seismic data. Construct the structurally lower γp axial surface, which dips at 53 deg.
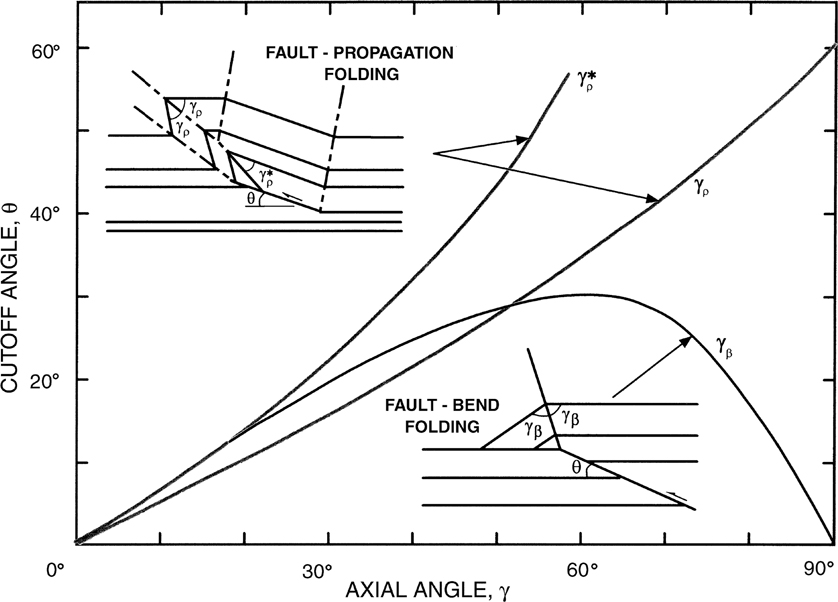
Figure 10-46 Fault propagation fold graph for a simple step-up from a decollement surface. (Modified from Suppe 1985.)
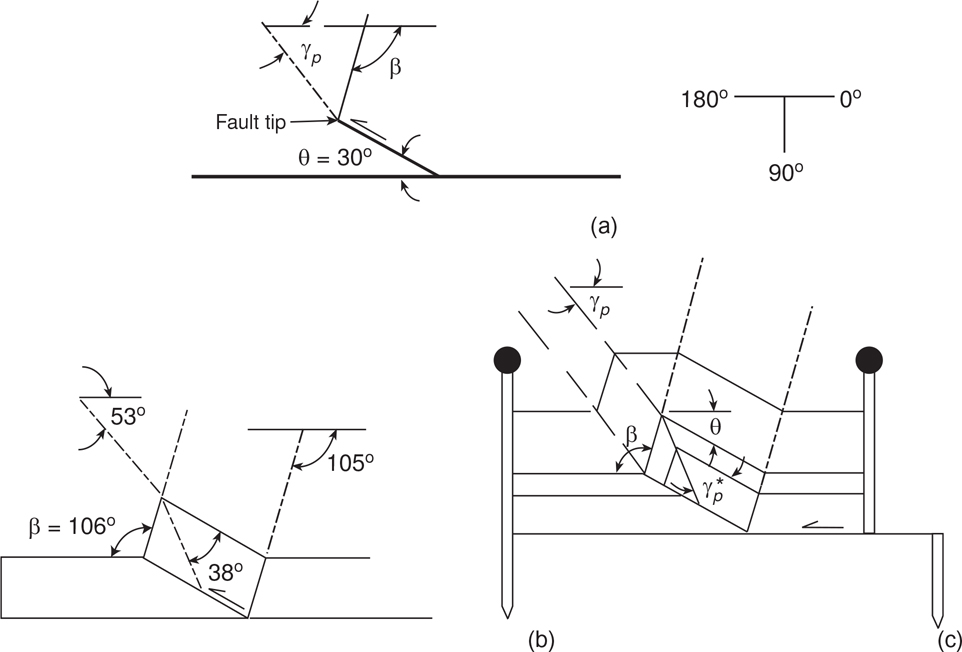
Figure 10-47 Fault propagation fold exercise.
The tip of the thrust fault and the front limb dip are used in determining the position of the branch point defined by the upper γp, B′, and γ*p axial surfaces (Fig. 10-47). The inclination of the front limb (β) is defined by
so the frontal limb inclination in this case is 106 deg (Fig. 10-47b). Draft a flat horizon to the left of the fault tip and then, using β = 106 deg, project the horizon upward from the fault tip. The position of the branch point is then located by projecting that same horizon, which is above the fault flat and on the level of the fault tip, across the fold’s back limb. This horizon is bent upward at the active axial surface at the base of the ramp (surface B, Fig. 10-43). Bisect the angle between the ramp and the flat to determine the position and inclination of the axial surface (105 deg in Fig. 10-46b). Then project the horizon parallel to the fault ramp, upward to the intersection with the front limb dip panel that was projected upward from the fault tip. The projected horizons intersect at the branch point (Fig. 10-47b). Next, the structurally higher γp axial surface (53-deg dip) can be drawn from the branch point. The γ*p axial surface (38-deg dip) can be drawn from the branch point into the core of the fold and to the fault (Fig.10-47b). Then draft the axial surface at the top of the back limb upward from the branch point, parallel to the axial surface at the base of the back limb. The elements of the structure are now complete, and additional layers can be projected throughout the structure. The line lengths then can be measured for area conservation between pinpoints (Fig. 10-47c).
Determining Structural Styles to Reduce Risk Using Qualitative and Quantitative Techniques
As structural style affects wellbore position and reservoir size, the correct identification of structural styles can increase production and reduce costs and risks (Kostenko et al. 2008). There are two major end-member structure styles: (1) fault bend folds and the related shear fault bend folds and (2) simple fault propagation folds (Suppe 1983; Suppe and Medwedeff 1990; Bischke 1994a; Shaw et al. 2005) (see Figs. 10-37 and 10-43). In particular, the recognition of an optimal wellbore plan, relative to the steep limb associated with fault propagation fold styles, is likely to increase production and reduce costs (Kostenko et al. 2008). Variations on these two major structural styles exists and are described in detail in Shaw et al. (2005) and Hughes and Shaw (2014). Here we concentrate on the end-member structures, which should help geoscientists recognize general structural styles and, in particular, fault propagation folds (Fig. 10-41) from other structural styles.
When examining these two major fold styles, geoscientists should recognize that each fold style has dependent geometric properties. For example, the amount of repeated section is related to the amount of throw, fault dip, and bed dip (Chapter 7, or Fig. 10-55), and structural relief is related to the amount of displacement. Also, these geometric parameters differ for the two major fold styles, and these differences are discussed in detail in the following sections. However, and regardless of structural style, all of the measurements of the geometric components should be consistent with each other. The measurements proposed are meant to be precise and to detect minor structural-style differences. The measurements can also be used to confirm interpretations, detect miscorrelations, and have properties similar to quick-look techniques proposed by Tearpock et al. (1994) and Wilkerson and Dicken (2001).
Qualitative Observations for Determining Structural Styles
The two main structural styles are geometrically different and can often be distinguished on interpreted and well-imaged seismic sections. However, real data often complicate interpretations, and a good understanding of structural styles will result in optimal well locations. Thus, we shall study both qualitative and quantitative methods for distinguishing structural style. We discuss qualitative methods first.
In general, fault propagation fold structural styles are tight asymmetric structures (Figs. 10-41 to 10-43) that can have steep frontal limb dips that often do not image on seismic (consult Fault Propagation Folds section). This nonimaged region is often interpreted as being faulted (Kostenko et al. 2008), whereas the main fault is often present at the base of the nonimaged region. The fault associated with these structures dies upward into the core of the fold, which means that the thrust fault decreases its displacement toward the surface. This has the effect of increasing the structural relief at shallower depths, while increasing reservoir size.
In contrast, fault bend fold structural styles are more symmetric than fault propagation fold styles and typically have wider crests, which may result in larger reservoir sizes than fault propagation folds. In fault bend folds, the fault typically bends downward before surfacing, and the displacements on the flatter dipping portions of the fault do not die out (Hughes and Shaw 2014) (Figs. 10-34 to 10-37). This has the effect of maintaining the amount of the structural relief. In other words, on fault bend folds, the structural relief remains about constant from the crest of structure to the base of the limb. On fault bend folds, which have horizons that are horizontal or restored to the horizontal, the structural relief equals the throw and the repeated section (Fig. 10-48). Repeated section is the vertical distance or vertical separation from the hanging wall horizon to its corresponding footwall horizon (Chapter 7, Fig. 7-28).
Figure 10-48 (a) A balanced end member, fault bend fold model that ramps off of the horizontal horizons. In this most basic of models of horizontal and uniform thickness beds, the structural relief (SR) equates to the throw (T) and repeated section (RS). Horizons can be projected from the hanging wall into the footwall to measure the projected repeated section. Also, the displacement or dip slip = SR/sin (bed dip). Real structures can be compared to the modeled SR and RS data on an SR/RS versus depth (Z) plot (see Bischke 1994b). On this end-member fault bend fold model, the measurements plot as a horizontal line and the % difference = 0.0. (b) A balanced end member, fault propagation fold model that ramps off of horizontal beds. In this end member model, the structural relief at the back and front of the structure decreases with increasing depth (Z), while the repeated section increases with increasing depth. This geometry contrasts with fault bend folds (Fig. 10-45a), as shown in the SR/RS versus depth (Z) plot. Furthermore, the % differences are 50% to 200% and not 0.0%, and thus % differences help determine structural styles. (Published by permission of R. Bischke.)
Quantitative Methods for Determining Structural Styles
There are several quantitative methods for determining structure style, which must be consistent. One is to measure the displacements (vertical separations) of the horizons across the fault surface versus the distances along the fault surface (Hughes and Shaw 2014). The vertical separations are a measure of the dip slip on the thrust. On fault bend folds, the displacements on the ramping fault are about constant from the base of the ramp up to where the fault bends downward (Hughes and Shaw 2014). The displacements then decrease at the downward bend in the fault surface (see Figs. 3 and 6 in Hughes and Shaw 2014). In contrast to fault bend folds, on fault propagation folds, displacements on the ramping fault decrease upward and often die out before reaching the surface (see Figs. 9, 10, and 12 in Hughes and Shaw 2014).
Hughes and Shaw conclude that structural deformation mechanisms can transition along the fault surface and contain components of the end-member fold types (their Fig. 14). For example, on the same structure, shear fault bend folds (see Fig. 10-53 for an example) can transition to fault bend folds. On shear fault bend folds, the shear parallels the bed surfaces (Corredor, Shaw, and Suppe 2005, in Shaw et al. 2005). Furthermore, fault bend folds can exist in combination with fault propagation fold mechanisms. Our study supports their conclusions that many structures have different mechanisms.
The second method, described here, is to measure the vertical separation (Reid 1909 for definition, or see Fig. 7-28) in the form of repeated section (RS) from the hanging wall to the footwall, or the amount of the structural relief (SR) for each significant horizon. The structural relief is the vertical distance from the top to the base of the limb of the structure (Fig. 10-48a and b), often defined by an inflection point. Another method is to measure the throw (T).
Next, plot these measurements on a structural relief or on a repeated section versus depth (Z) graph (Fig. 10-48a) (also see Chapter 13). Measurements of structural relief can be obtained from either limb of the fault bend fold, although the back, or the more gently dipping limb, may image better than the frontal limb. This procedure is different from studying the slip on the fold and complements Hughes and Shaw’s (2014) methods of measuring and confirming the displacements on reverse faults. Furthermore, in the hanging wall, the structural relief measurements can be applied to uninterpreted horizons. This is particularly valuable if the footwall horizons do not image or if velocity problems exist that distort geometry (Sheriff 1977, 1980), thus making displacement measurements possible. In addition, the core in the frontal limbs of fault propagation folds often do not image, as the front limb can be near vertical, thus containing incoherent data (see Storti et al. 2005) (Fig. 10-41).
A number of structural geometries or components on folds are geometrically related to each other and must be consistent with each other. In Chapter 7, we discuss the geometric relationships of repeated section and throw. For example, using Figures 7-27 and 7-28, we derive equations for repeated section (Eqs. [7-4] and [7-5]) that relate repeated section to throw using bed and fault dips. In turn, throw is also related to displacement or slip on the fault and to fault dip (Figs. 7-27 and 7-28). In addition, structural relief is related to fault dip, shape, and displacement (Figs. 7-27, 10-34, and 10-48a and b). We start with ideal, generic end-member examples of fault bend (Fig. 10-48a) and fault propagation (Figs. 10-48b and 10-49a) folds before studying well-constrained real examples.
Figure 10-49 (a) Fault propagation fold displaying the structural relief (SR) in the front limb from the hanging wall to the footwall. (b) On this SR and vertical distance (VD) versus depth (Z) plot, the SR decreases with increasing depth (Z), and the SR % difference is large at 78%, indicating that the structure is a fault propagation fold. The structural style is confirmed as the VD from the hanging wall fault propagation folds horizon to the fault surface also decreases with increasing depth (Z) on the plot. At depth, the VD on the fault surface = 0.0, and thus the VD % difference = 200%. (Published by permission of R. Bischke.)
A review of existing depth-corrected, 3D contractional structures indicates that there is value in measuring more that one of the structural components to determine the precise structural style. In other words, different conclusions concerning fault interactions or mechanisms are possible if geoscientists measure a combination of dip-slip displacements, throw, structural relief, and repeated section. Multiple procedures, such as quick-look techniques (Tearpock et al. 1994; Wilkerson and Dicken 2001), can rapidly detect horizon miscorrelations and retrodeformability. Also, 3D vertical separations are simpler to measure than 2D displacements on fault surfaces. This is particularly true when interpreting vertical well log data.
Figure 10-48a is a balanced, end-member fault bend fold on a scale of one to one. The vertical change in depth of the limbs of the fold define the structural relief, labeled SR1 to SR3 for the top three horizons (H1 to H3). One simply measures the vertical distance of the SR, as indicated by the vertical arrows. The SR measurements are taken at an inflection point on the dipping limb to the crest of structure. Often, the more gently dipping back limb images better that the front limb, and therefore measurement are often better conducted on the back limb of folds. Furthermore, when measuring SR, the beds need not be horizontal.
Two wells penetrate the generic crest of structure, with Well No. 1 penetrating the top of H4. The generic well thus encounters repeated section in the footwall, labeled RS4. The top or crest of H4 in the hanging wall is projected to Well No. 2 in order to measure the projected repeated section, RS4. In addition, Well No. 2 intersects the top of H3 in the hanging wall and the footwall, creating RS3. In this case, as the beds are horizontal, the repeated section equals the throw. Notice that, for uniform thicknesses and horizontal beds, SR1, SR2, and SR3 equals RS3, RS4, and throw (T). Thus, when graphed on a repeated section/structural relief versus total depth (Z) correlations graph, the result is a horizontal line, indicating that the structural relief and repeated section are constant (lower Fig.10-48a). To determine structural style, these measurements can replace or complement measuring the displacements on the fault surface. Hughes and Shaw (2014) concluded that on the ramp, the displacements on end-member fault bend folds are constant.
In the section on real examples, and in the generic examples presented in the next paragraph, we present the % difference of the data. The % difference is the difference between the largest and smallest length measurements divided by the averaged sum of the difference between the largest and smallest length measurements. These values quantitatively define the percentage change of the measurements. On real fault bend folds, the % differences may approach zero (Figs. 10-48a, 10-51a, and 10-52). The % difference measurements help define structural style and also detect complex deformation histories (Hughes and Shaw 2014).
When measuring a repeated section on structures that exhibit large displacements and repeated section (and ramp off the footwall horizon), measure the repeated section at about the same point where you measure the structural relief (Figs. 10-50 and 10-51). This procedure is similar to drilling a vertical well. However, in some cases, it may be more convenient to measure the repeated section on either the forward or trailing side of the dip panel (Fig. 10-48a and b). Using an axial surface inflection point works best. In real structures, the hanging wall beds need not parallel the footwall beds as the fault ramps through the footwall, and thus the structural relief need not equal the repeated section. In the examples shown in Figures 10-50 and 10-51, the repeated section is larger than the structural relief.

Figure 10-50 Thrust fault ramps through footwall and bends downward. This bend causes the structural relief to be different from the repeated section. The % differences are, however, about equal to zero, indicating that this structure is a fault bend fold. (Published by permission of R. Bischke.)

Figure 10-51 (a) A depth-corrected 3D seismic line is a dip line of the well-imaged El Furrial Fault-Bend Fold, Venezuela. The repeated section and structural relief data were measured at about the same position (Morales et al. 2005). (Reprinted by permission of the AAPG whose permission is required for further use.) (b) Strike line through the frontal panel of the dip line shown in Figure 10-51a is plane “B.” On Figure 10-51b, the dip line shown in Figure 10-51a crosses the strike line on plane “A.” The thrust fault is located where dipping beds terminate over horizontal beds.
In contrast to fault bend folds, fault propagation folds tend to behave differently, and the structural relief will not remain constant with increasing depth (Figs. 10-48b and 10-49a). While at shallow depths, the structural relief can be about constant, with increasing depths the structural relief decreases as the repeated section increases (Fig. 10-49b). Notice in Figure 10-48b that in the frontal portions of the hanging wall, the vertical distance (VD), measured from the back limb to the fault surface, decreases to zero. This vertical distance is typically measurable even if the seismic data in the hanging wall are incoherent. In addition, where seismic data are lacking, geoscientists can measure the vertical distance from the back limb to its corresponding projected correlation in the footwall (Fig. 10-49a).
In Figure 10-48b, measuring repeated section is identical to measuring the vertical separation at the fault surface to the corresponding horizon in the footwall (Figs. 6-35, 7-26, 7-27, and 13-19). In contrast to the fault bend folds, in the fault propagation fold structural styles, the % difference will be high and can exceed 50%. Thus, % difference measurements should help distinguish structural style.
Real Fault Bend Fold and Fault Propagation Data
Repeated section can exist in both well log and seismic section data. Here we study outcrop data, depth-corrected seismic data, and well-constrained well log examples that use correlations, surface dip, and dipmeter data. We start with constrained fault bend fold data before addressing fault bend fold data. In all of the real data calculations, the % difference measurements include all interpretation measurements, which includes existing structural interpretations, miscalculations or data problems, such as lateral velocity changes and poorly imaged footwalls. After increasing the size of the figures to 400% and 200%, the ability to measure with a magnifying glass is about 1 part in 60, or about 1.7%. In Chapter 7, the repeated section is defined as AE, and the throw as AC, and this convention is followed in the equations. The repeated section (AE)/throw (AC) ratio (Fig. 10-55) will be calculated when possible for each structure to confirm the interpretation.
Fault Bend Folds
Tiehchanshan Anticline, Western Taiwan.
The Tiehchanshan Anticline is constrained by well log correlations and surface dip data. Based on reasonable correlations and lithologies, Suppe and Namson (1979) conclude that the TCS-34 well has 700 m of repeated section. According to measurements conducted on their cross section, the repeated section at the well is about 685 ft (1 m = 3.28 ft). Thus, the % difference is 2.2%. The measured AE/AC is 690/1150 = 0.6, and the AE/AC value calculated is (1 − tan(5 deg))/tan (average dip 13.5 deg) = 0.62. The calculated values are within the calculated values of the sine function and measurement errors.
Depth Corrected El Furrial 3D Seismic, Monagas Venezuela.
The data shown in Figure 10-51 are from measurements collected from the well-imaged giant El Furrial Venezuela structure (Morales et al. 2005, in Shaw et al. 2005). The structural relief and repeated section measurements are from the prolific Oligocene to the less prolific Middle Cretaceous section. The structural relief is measured from the southeast side of the southeast dipping panel adjacent to the crest of structure. The repeated section data are collected from the hanging wall reflections at the base of the structural relief data in the hanging wall to the corresponding footwall reflections.
Figure 10-52 shows repeated section and structural relief calculations in kilometers (1 km = 3281 ft) along with the % differences for the structural relief and repeated section. Structural relief % differences for the southeast side of the dipping panel adjacent to the crest are equal to zero. The repeated section % differences data are collected at the same horizontal position as the structural relief data and are equal to a % difference of 1%. Thus, along this seismic line, the structure is a classic fault bend fold.

Figure 10-52 Structural relief/repeated section plot for the super-giant El Furrial, Venezuela, structure (Morales et al. 2005). Measurements from a 3D line indicate that at this location the structure is a classic fault bend fold. The R2 repeated section data are close to 1.0, and structural relief data are equal to zero. (Published by permission of R. Bischke.)
Depth-Corrected 3D Seismic Line from Deep-Water Nigeria.
This seismic line from Nigeria (Corredor, Shaw, and Bilotti 2005, in Shaw et al. 2005) is a shear fault bend fold, which is related to the end-member fault bend fold data. The two structures differ in that the back and front limbs of shear folds are sheared parallel to the horizons (see sheared profile on the back limb of Fig. 10-53). Shear folds form in recently deposited, unconsolidated, and plastic shales subject to gravity sliding (Corredor, Shaw, and Bilotti 2005).

Figure 10-53 A well-imaged 3D and depth-corrected line of a shear fault bend from the deep-water Nigeria fold-thrust belt (in Corredor, Shaw, and Suppe 2005, in Shaw et al. 2005; reprinted by permission of the AAPG, whose permission is required for future use.)
Figure 10-54 is a throw (T) and structural relief (SR) versus depth (Z) plot of the a to b back limb of the structure that was subject to uniform shear (Fig. 10-53). The plot of the roughly uniform-thickness, red to green horizon data have low % differences. The throw % differences are 5.7%, and the structural relief % differences are 4.8%, indicating the structure is a fault bend type of fold.
Figure 10-54 A throw and structural relief plot of the shear fault bend fold imaged in Figure 10-53. The data come from the uniformly sheared back limb of the structure and have low % differences. This indicates that the structure is related to fault bend folding. (Published by permission of R. Bischke.)
Fault Propagation Folds
The repeated section/throw equations for fault propagation folds can be different from the equations described in the discussion of how to calculate throw versus vertical separation in Chapter 7 under Compression. Also, Eq. (10-1) changes for hanging wall horizon dips greater than 90 deg. Figure 10-55 contains three dips.
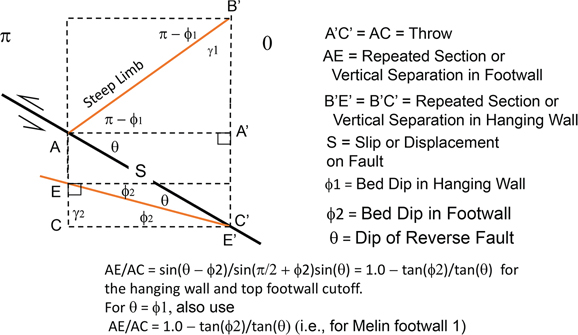
Figure 10-55 As fault propagation folds are not similar to fault bend folds, different repeated section formulae are required to predict repeated section/throw calculations. The figure allows for a calculation of fault propagation folds that have a difference in dip between the hanging wall and footwall. Consult text for details. (Published by permission of R. Bischke.)

Thus, relative to the hanging wall repeated section, a repeated footwall section ratio B′C′/AC exists (Fig. 10-55). We derive utilizing the law of sines and trigonometric identities:
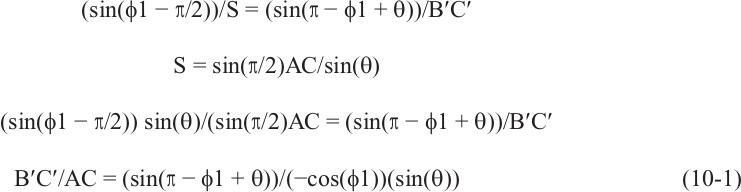
Outcrop of Fault Propagation Fold Dunlap, Tennessee.
As stated previously, fault propagation folds are geometrically different from fault propagation folds. The first example is a fault propagation folds from an outcrop in the Appalachian fold-thrust belt. We measure a photograph interpreted by Boyer (1986; see his dashed lines or, in this book, Fig. 10-42). The structural relief on the horizon above the shale section establishes the scale on Figure 10-56. The datum for the depth (Z) measurements are relative to the top of the Boyer’s Figure 6.
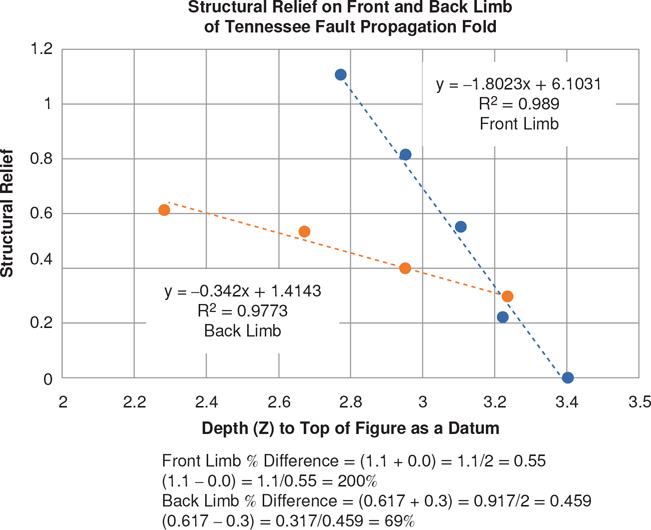
Figure 10-56 A back limb and front limb structural relief plot for an outcrop in Tennessee (Boyer 1986). The structural relief measurements exceed 50%, indicating that the structure is a fault propagation fold style. (Published by permission of R. Bischke.)
Relative to the fault surface, the measurements taken from Boyer’s figure and plotted on Figure 10-56 show that the structural relief on the front limb of this fault propagation fold decreases to zero at the thrust fault (e.g., examine the arrows in the hanging wall of the front limb of Fig. 10-48b). This geometry is typical of fault propagation folds. In contrast to fault bend folds, the % difference calculation is large at 200%. The back limb structural relief also corresponds to fault propagation folding, with the % differences decreasing with depth. The % difference is high at 69%.
Melin Anticline, Western Taiwan.
The Melin Anticline, interpreted by Suppe and Medwedeff (1990), is constrained by surface dips, dipmeter well logs, repeated section, and well log formation correlations. Our measurements of the back and front limb of the structural relief/repeated section data are shown in Figure 10-57. The repeated section data are measurements taken from the hanging wall to the equivalent footwall correlation. Again, the % differences are large at 53% for the structural relief and 142% for the repeated section.

Figure 10-57 The Melin structure is constrained by surface and well log dips, repeated section, and well log correlation data (Suppe and Medwedeff 1990). This balanced structure has % differences in excess of 50%, consistent with FPF. (Published by permission of R. Bischke.)
For the top Chinshui Shale, the hanging wall and footwall measured repeated section/throw ratio = 0.882, and the calculated values are AE/B′E′ = 0.895 (Fig. 10-55 and Eq. 10-1). The footwall wall repeated section/throw measurements can be compared to the calculated values, and thus B′E′/A′C′ = 0.833. For the top Chinshui Shale, calculated values for the hanging wall = 0.835.
Fault Propagation Seismic Fold from Nigeria.
This depth-corrected and well-imaged seismic line is from Nigeria (Hughes and Shaw 2014) (Fig. 10-58) and was interpreted as a fault propagation fold. The front limb structural relief was measured at the same position as the repeated section. As both data sets contain zeros, the % differences are large (Fig. 10-59), and both the structural relief % difference and the repeated section % difference are 200%. This fold has all of the characteristics of fault propagation folding (Hughes and Shaw 2014), although some interpreters may conclude after examining the structure that the structure is a fault bend fold!

Figure 10-58 A well-imaged and depth-corrected 3D seismic line from Nigeria (Hughes and Shaw 2014). The yellow upward arrows depict structural relief, and the downward orange arrows depict repeated section. (Reprinted by permission of the AAPG whose permission is required for further use.)
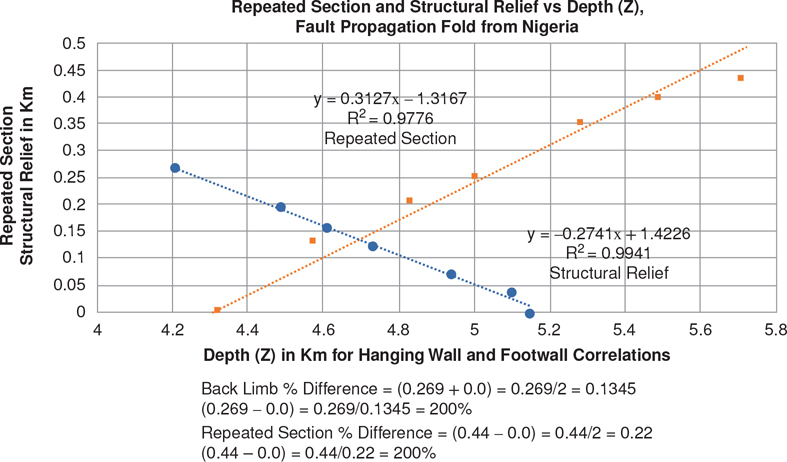
Figure 10-59 A structural relief/repeated section plot from a 3D seismic line from deep-water Nigeria (Hughes and Shaw 2014). Measurements of the repeated section and structural relief data are taken from the same point on the fault and along the fold. As the structural relief and repeated section % differences are 200%, this structure appears to be a classic fault propagation fold.
Conclusions
This study of structural styles concludes that several or all of the geometric components should be measured to more precisely define structural styles. These measurements include fault displacements, throw, structural relief, repeated section, and repeated section/throw measurements and calculations. These geometric properties will detect problem interpretations or correlations and will establish a sound basis for confirming structural styles when the structural style is not obvious. This problem particularly occurs in the frontal limb of fault propagation style folds (Bischke 1994a; Kostenko et al. 2008), which can result in costly errors.
The two major end-member styles, fault bend and fault propagation folding, exhibit distinctly different geometric properties. Fault bend folds from reasonably well-constrained structures contained % difference calculations of approximately 0.0 and did not exceed 6%. Conversely, fault propagation folds had structural relief % differences greater than 50% and repeated section % differences that approached or equaled 200%.
Imbricate Structures
As the thrust belt moves progressively over the foreland, there is a tendency for new thrust faults to form near the toe (front) of the thrust belt and for these thrusts to seek a lower structural level. Where a thrust fault forms below a pre-existing fault(s), motion along the deeper fault will cause the shallow fault(s) and its overlying structure(s) to fold. The deformation can produce some rather interesting and complex geometries of stacked folds (Fig. 10-60). Thrust faults that form at a higher structural level and above the newly formed imbricate thrust faults have been, perhaps inappropriately, called out-of-sequence thrusts.
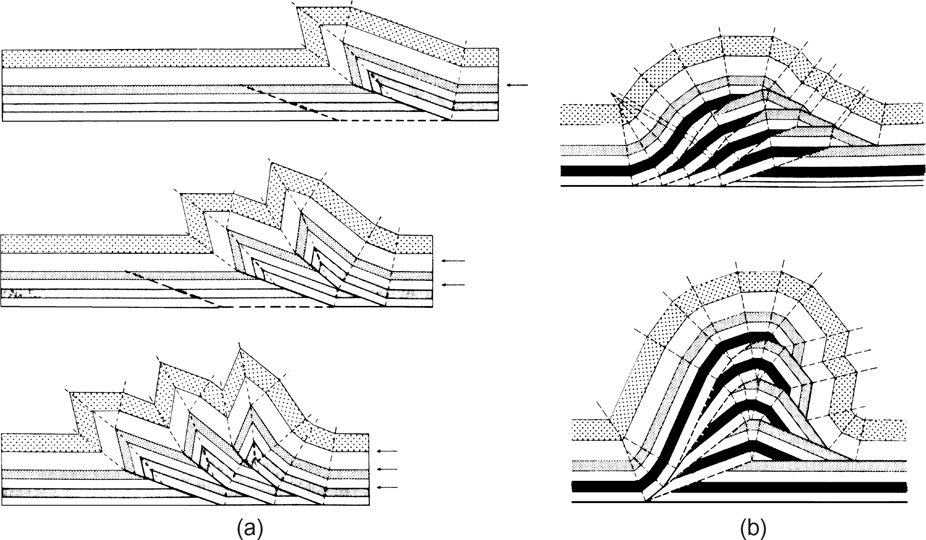
Figure 10-60 Diagram showing different types of duplexes. (a) Stacked fault propagation folds. (b) Foreland and anticlinal stacked duplexes. (From Mitra 1986; AAPG©1986, reprinted by permission of the AAPG whose permission is required for further use.)
Two possible procedures exist to study imbricate structures: the simple forward model in which the interpreter defines the amount of slip, and the more complex inverse model. In the more useful inverse modeling, the amount of slip is constrained but is unknown to the interpreter, which makes the problem more difficult. We address the forward modeling before proceeding to the inverse model.
This complex process is best described through example. We first assume that a fault bend fold formed near the front of a thrust belt, as shown in Figure 10-61a. In this example, we assume that faulting formed ramp AB and that the ramp angle is 20 deg. We can now determine the frontal dip panel angles by using the methods developed in the section on fault bend folds. We also assume for purposes of demonstration that, at a particular time, the fault breaks through at the lower level and another ramp forms in front of the ramp that formed the fault bend fold. The new ramp along the lower decollement is ramp CD in Figure 10-61b.
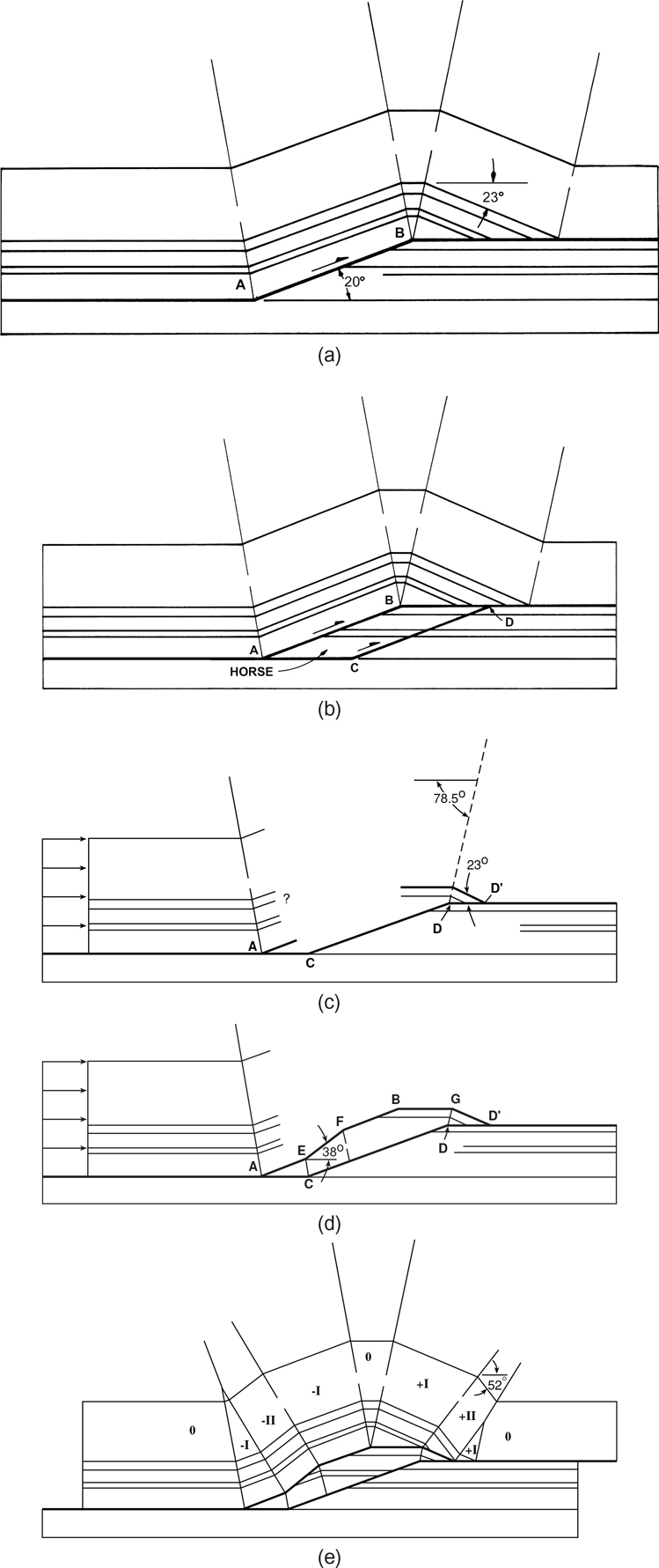
Figure 10-61 (a)–(e) Duplex exercise, forward model.
This wedge-shaped structure, which is completely surrounded by ramps AB and CD and flats BD and AC, is called a horse (Boyer and Elliott 1982). If several horses move up their ramps, then they form a duplex of folded imbricate thrusts (Fig. 10-60b).
We assume for purposes of demonstration that the thrusting on the lower fault has progressed to a stage such that the original distance between points A and C has been exactly halved, which means that only a portion of the rhomb-shaped horse has moved onto the upper flat (Fig. 10-61c). As the frontal part of the rhomb-shaped horse moves up the ramp, it will bend in the same manner as layers deform during fault bend folding. Thus, for this part of the deformation, we can determine the deformed shape of the horse using the kink method and the techniques developed in the section on fault bend folds. It now follows that as the horse block moves up a 20-deg ramp and onto an upper flat, it will have the same frontal dip angle (β) as the fault bend fold had when it moved up the 20-deg ramp AB in Figure 10-61a. Therefore, frontal dip angle can be determined to be 23 deg from Figure 10-38 (or from Table 10-1). The amount of slip consumed by the bending of the layers within the frontal dip panel of the horse can be determined from Figure 10-40, which in this case is about 0.87 of the total slip. Therefore, after deformation, the distance DD will be equal to 0.87 of the distance 1/2 AC in Figure 10-61b.
Next, we bisect the angle between the part of the horse that was bent (where it rode up over the top of the ramp) and its undeformed portion. This produces an axial surface with a dip of 78.5 deg. Then we project the uppermost portions of the horse to the left. Bed length consistency requires that the layers be the same length before and after deformation, so length BD before deformation (Fig. 10-61b) should be equal to length BD′ after deformation (Fig. 10-61d).
The problem of the deformed horse can now be resolved. The upper deformed part of the horse located near point B (Fig. 10-61d) rode up ramp CD without being deformed. As the cutoff angle of ramp AB is 20 deg, the upper segment of ramp AB can be projected downward at a 20-deg angle in Figure 10-61d (i.e., line segment FB). Similarly, the lower portion of ramp AB (located near point A of Fig. 10-61b) slid along the lower flat without being deformed, and thus the lower part of the ramp AB can be projected upward at a 20-deg angle (Fig. 10-61c). The central part of the horse, however, has been subject to deformation as the wedge-shaped horse moved up ramp CD and through axial surface EC. Axial surface EC is pinned to the lower footwall cutoff at point C and is an active axial surface. Ramp CD has a 20-deg initial cutoff angle, so the bisecting axial surface EC dips at 80 deg (Fig. 10-61d and e). It also defines the extent of line AE.
We have now determined that as the deformed fault ramp AB moves through axial surface EC, it must deform (bend upward). Ramp AB initially dipped at 20 deg before deformation, so it must dip at an even higher angle after deformation. If a 20-deg dipping line (line AB) moved up a 20-deg dipping ramp (line CD of Fig. 10-61d), one might incorrectly conclude that the central deformed portion of fault ramp AB (line segment EF) would dip at 40 deg. We use Table 10-1 to provide the correct dip angle for line EF.
The following is an example of the rationale for Table 10-1. In the section on fault bend folding, we learned that in order to maintain line lengths, the angle β, the dip of the frontal limb, must be greater than the (initial) cutoff angle θ. This relationship must be maintained on every structural level within imbricate structures. Thus, as the frontal part of the horse rides over the top of the ramp, it rotates forward to a dip angle of 23 deg (Fig. 10-38, or Table 10-1). This rotation causes the overlying beds to dip forward at a higher angle (dip panel +II in Fig. 10-61e). The dips at the higher structural level experience a quantum increase in dip (Suppe 1980, 1983). In other words, the insertion of the horse onto the upper flat will cause the beds above it (panel +II) to dip at an angle that is greater than twice 23 deg, or in this case 52 deg, as determined from Table 10-1. In Table 10-1, the central column contains values for the cutoff angle θ, and the other columns provide the calculated dips within each panel of the fold. Thus, for a 20-deg cutoff angle, the front limb dips at 23 deg and at 52 deg in panels +I and +II respectively. In order to maintain line length and formation thickness, the strata above the horse will shear in such a manner that an increase in dip in the frontal panel is accommodated by a decrease in the expected dip in the back panel. Thus, the compensating dip of line segment EF (panel −II) in Figure 10-61d and e is 38 deg rather than 40 deg (Table 10-1). The dip panels III through VII in Table 10-1 relate to higher-order duplex structures.
The length of line AE was defined previously by constructing the axial surface at point C in Figure 10-61d. Point F is determined from the amount of slip on the lower fault. Measure that slip up the ramp and draw the inactive axial surface parallel to the one at point C; then draw line EF at a dip of 38 deg (Table 10-1) upward to the axial surface. Complete the deformed fault surface by drawing line FB (point B was determined above). The inactive axial surface beneath F will be the line at which you project horizons within the horse downward and parallel to the lower ramp, as in Figure 10-61e.
The strata above deformed ramp AB will parallel that surface and bend at axial surfaces located at points E and F. Bisect the angles along the deformed upper ramp (angles AEF and EFB in Fig. 10-61d) and complete the dip domains toward the surface (Fig. 10-61e). The crest and the front limb (with a 23-deg dip) of the original fold were above the upper fault flat, to the right of point B in Figure 10-61a. As described previously, part of this frontal dip panel of the original fault bend fold was subsequently deformed by the frontal portions of the horse, and it dips at 52 deg (Fig. 10-61e). However, the part of the horse between points F and G (Fig. 10-61d) is undeformed, so the dips of the overlying strata and the axial surfaces at B are maintained from the original fold (dip panels −I, 0, and +I in Fig. 10-61e). A small dip panel (+I) exists to the right of panel +II and has a dip equal to that of the original front panel (23 deg), as it is a part of the frontal limb of the original fold that was not deformed (Fig. 10-61b). The axial surface on the right of small dip panel +I has an inclination of 78.5 deg, maintained from the original fold. The axial surfaces bounding panel +II are placed at bends in the upper fault surface and drafted at inclinations that bisect the adjacent dips. Complete the cross section by using dip data in Table 10-1 to draw the horizons in panels −I, +I, and 0 (flat). The finished, balanced cross section in Figure 10-61e depicts a duplex structure.
Although this exercise may at first seem to be an unnecessary complication, we use these small changes of dip to our advantage in what is called dip spectral analysis (Suppe 1980, 1983). Dip spectral analysis can be used to interpret poorly imaged subthrust plays.
Consider the geometry present in Figure 10-61e, which has several implications concerning petroleum exploration. Assume that the thin horizon above the lower flat is a productive reservoir horizon. Notice that this reservoir can be intersected on two structural levels, resulting in two potential plays. The first play is the closure associated with the original fault bend fold. The second play is a partial closure located within the horse, and thus its prospectivity would depend on the trapping mechanism or the permeability of the beds above the thin reservoir horizon.
Dip Spectral Analysis.
This section discusses the method to locate potential subthrust plays in practice. We learned from the previous imbricate structure exercise that for uniform step-up angles, and as one moves up the structural pile, the dips at the front of the imbricate structures increase at an increasing rate. Furthermore, the back dips, whereas exhibiting a corresponding increase, do so at a decreasing rate. Therefore, the frontal dips exhibit a unique quantum increase in dip (in our case, 52 deg is greater than twice 23 deg), whereas the back dips exhibit a unique quantum rate decrease in dip (Table 10-1). These unique changes in dip allow us to estimate the number of subthrusts and their approximate position. For example, in Figure 10-60b, the duplex structure in the lower figure has four different back dips relative to the flat regional dip. This means that the duplex has four or more thrusts and four or more potential repeated sections.
Notice that in Figure 10-61e the final structure exhibits three frontal dip panels or domains (labeled +I, +II, and +I) and three back dip panels (labeled −I, −II, and −I) that are separated by a region of initial dip (panel 0). In nature, detailed surface mapping across the structure shown in Figure 10-61e could result in the topographic section shown in Figure 10-62a. In this figure, the following dips occur from left to right: 0, −38, −20, 0, 23, 52, 0, −20, −20, −20, and 0 deg (designating leftward dips as negative). If a regional dip of 5 deg to the left were to exist, then the corresponding dips would be −5, −43, −25, −5, 18, 47, −5, −25, −25, −25, and −5 deg. Regional dip should be removed prior to dip spectral analysis. All angles are determined relative to regional dip, but by removing regional dip, we can conveniently use angles measured from the horizontal, as given in Table 10-1. The resultant dips corrected for 5-deg regional dip are 0, −38, −20, 0, 23, 52, 0, −20, −20, −20, and 0 deg.
Figure 10-62 (a)–(d) Duplex exercise, inverse model.
We have shown that higher dips exist at the front of the structure, whereas lower dips occur at the back (Fig. 10-61e). Thus, the 52-deg dip and its associated 23-deg dip are forward dips, whereas the −38-deg dip and its associated −20-deg dip are backward dips (see Table 10-1). As there are two forward dips, the 52-deg dip represents a +II domain, and the 23-deg dip represents a +I dip domain. These numbers, each of which represents an individual dip domain, can be compared to Table 10-1 (line 13) to indicate that there are two thrust faults ramping at 20 deg, causing second-order frontal and back dips of 52 deg and −38 deg respectively, and first-order frontal and back dips of 23 deg and −20 deg respectively, in the upper structure. If three faults are present, then we would expect an additional forward dip of about 98 deg and a back dip of about 53 deg (Table 10-1). As only two forward dips exist in our example, Table 10-1 suggests that only two thrust faults are present. Therefore, surface and subsurface data can be compared to Table 10-1 in order to determine the number of imbrications that may exist in the area of study. The data could be surface bed dips, subsurface dipmeters, and/or depth-corrected seismic data.
Let us proceed to solve the structure presented in Figure 10-62a, which is based on the forward model completed in Figure 10-61e, but uses only surface outcrop data. This inverse model is more complex and requires inverted thinking; thus, the interpretation process is more difficult.
After analysis of the surface dip data, the first task is to determine the dips of the axial surfaces, which separate the observed dip domains. Once the related dips within each of the dip domains have been averaged, as was described in the section on the kink method, the dip of the axial surface between given adjacent dip domains can be determined from the following formula:
where
θ = dip of axial surface taken counterclockwise from the horizontal

For this equation only, structural dip is taken to be negative if it is to the right. It would fall within the 90-deg to 180-deg quadrant, as defined in Figure 10-62a. If dip is to the left, it falls within the 0-deg to 90-deg quadrant and is assigned a positive value in the equation. The dips of the axial surfaces for the appropriate dip domains presented in Figures 10-62a and 10-61e were calculated and are presented in Table 10-2. For example, at the top of the hill on the left, a 0-deg dip exists adjacent to a 23-deg dip to the right (Fig. 10-62a). These two dips represent a 0 dip domain and a +I dip domain (Fig. 10-61e and Table 10-1). They are separated by a dip domain boundary, which is the 0 +I axial surface. Thus, the 0 +I dip domain boundary dips at (0 − 23 + 180)/2 = 78.5 deg (Table 10-2).
Table 10-2 Axial Surface Calculations
Dip domain boundary* |
Dip of axial surface (in degrees) |
|
|---|---|---|
–I – II |
(38 + 20 + 180)/2 |
119.0 |
0 – II |
(0 + 38 + 180)/2 |
109.0 |
0 – I |
(0 + 20 + 180)/2 |
100.0 |
0 + I |
(0 – 23 + 180)/2 |
78.5 |
0 +II |
(0 – 52 + 180)/2 |
64.0 |
+ I + II |
(–23 – 52 + 180)/2 |
52.5 |
*Dips and dip domains are taken from Fig. 10-46a
These axial surface dip calculations are best applied to the solution of problems using a method that was suggested by John Suppe and is shown in the lower portion of Figure 10-62a. First, calculate the dips of all axial surfaces for the adjacent pairs of dip domains. These are shown in Table 10-2. Then create a reference set of axial surfaces, as shown in Figure 10-62a. The dip of each axial surface is projected downward from a central point and labeled. The dip of each axial surface is measured off in a counterclockwise direction. Two triangles can now be aligned with the axial surface dip data and slid into any position on the cross section that the interpreter desires. This procedure makes the interpretation process more rapid.
Possessing the dip data set presented along the topographic profile in Figure 10-62a and the knowledge gained from the solution to the problem presented in Figure 10-61e will not allow us to arrive at a unique solution to our problem. Trial and error and some guessing are required to solve the problem presented in Figure 10-62a. The advantage of solving this problem is obvious for areas where seismic data fails to image imbricate structures. It may result in the identification of duplex structures and generation of additional prospects and perhaps additional oil and gas discoveries.
Before proceeding further, notice that Figure 10-62a does not include the −20-deg dip panel above the lower flat, which is present in Figure 10-61e and which is to be expected from Table 10-2. This should make our problem more interesting and realistic. The 0 and −II data are included in Table 10-2 for reasons that will soon become apparent.
The first step in the solution of our problem is to examine the data from a geometric point of view. Two observations are critical to an accurate interpretation. First, the observed dips tend to follow the topographic slope, which is often the case in nature. Second, the beds above the thrust fault at the outcrop dip at about the same angle as the thrust fault, suggesting that a ramp is responsible for the 20-deg tilt to these beds. Therefore, the thrust fault can be projected from the outcrop downward to where it intersects the adjacent (0-deg) dip domain. But where is this point? It exists where the 0 −I axial surface intersects the projected thrust fault. The change in topography is used to position and project the 0–I axial surface with a 100-deg dip (from Table 10-2) downward to the point where it intersects the thrust fault, thus determining the base of the upper ramp (Fig. 10-62b, point A). In addition, we have predicted the structural level of the upper flat or decollement (Fig. 10-62b).
Looking at the dip data further, we see the 0-deg dip at the hilltop on the left and the 23-deg and 52-deg dips to the right. Using Table 10-1, we can infer that two 20-deg ramping thrusts create the observed 23-deg and 52-deg forward dips, and thus these two thrusts must be imbricated (i.e., stacked) in order to produce the observed quantum increase in dip. The data suggest that a 52-deg dip domain adjoins a 0-deg dip domain, and therefore, a 64-deg axial surface (between the 0 and +II domains of Table 10-2) is positioned at the appropriate change in topographic slope (Fig. 10-62b). We know that two dips exist to the left of the intersection of the 0 +II axial surface with the upper flat at point B. First, the structurally higher beds dip at 52 deg to the right, and second, a 23-deg deformed thrust must exist beneath the 52-deg dipping beds. This follows from a direct application of Table 10-1 and the theory that we presented earlier.
Consequently, at point B we interpret and construct a 52-deg dipping bed and the deformed 23-deg dipping fault (Fig. 10-62c). The 52-deg dipping bed and the deformed 23-deg fault are then projected up to the +I +II axial surface, which has a dip of 53 deg (Table 10-2) and is positioned at the break in topographic slope. To the left of this axial surface, the fault will be flat like that in an undeformed part of the older fault. Now the kink method is applied to the deformed horse block in order to map the forward dip within it, beneath and parallel to the deformed fault. An axial surface must extend downward from the kink in the fault. Given the adjacent dips of 0 deg and −23 deg, the dip of the axial surface calculates to be 78.5 deg (Table 10-2). A (0 +I) axial surface is drawn downward from the kink in the deformed fault to where it intersects the flat, thus locating point C in Figure 10-62c. The frontal portions of the deformed horse block have now been properly defined (i.e., we have separated the undeformed and the deformed regions of the horse block). Point C not only marks the position where the horse block has ridden onto the upper flat but also determines where the structurally lower ramp can be projected downward at a 20-deg angle (Fig. 10-62c, line EC).
Proceeding with the construction, the 52-deg dipping beds in panel +II above the horse can be projected from the +I +II axial surface at a 23-deg angle up to the 0 +I axial surface (Fig. 10-62c, point F). The axial surface was positioned from topographic data. The flat of the upper thrust is projected to the 0 +I axial surface to establish point G, which defines the edge of the horse block, or the top of the ramp on the original fault (Fig. 10-61a and d, point B). From point G, the upper fault can be projected downward at a 20-deg angle (defined by the dip data in panel −I to the −I −II axial surface (Fig. 10-62c, point H). This axial surface was positioned at a break in the topographic slope. The structural and fault dip must change at this axial surface, so the deformed fault is projected downward at a 38-deg angle, as defined by the dip data in panel–II, until the upper fault intersects the 0 −II axial surface (Fig. 10-62c, point I). This axial surface, with an inclination of 109 deg (Table 10-2), is located at a break in the topographic slope. Using the 0 −II axial surface as a bisector, project the upper fault to level out on the IJ structural level parallel to the overlying flat structural dip. The lower flat on the structurally lower fault still must be interpreted. An axial surface must exist between the −20-deg ramp and the flat. This surface calculates to have a 100-deg dip, and it must extend downward from point I. Thus, point E is located at the base of the ramp. The fault flat is then drawn to the left of point E.
Finally, the axial surface between points H and D is constructed parallel to active axial surface IE (Fig. 10-62c). It is the inactive axial surface within the horse. The length of the line ED should be the amount of slip on the younger fault (Fig. 10-61, distance EF), according to this interpretation.
What is the final result of our interpretation process? We have seemingly followed the methods with a result that is somewhat complex and confusing! Notice that the upper and lower faults do not merge on the same structural level (compare I to E, Fig. 10-62c). How can we fix this solution, and what features should we look for when attempting to arrive at a more satisfactory solution? First, check the slip on the upper flat (CB) of the younger fault to the slip up the ramp (ED). They are incompatible. Using Figure 10-40 to determine the slip correction factor for a step-up angle of 20 deg., line CB should be 0.87 of ED, or CB/0.87. However, in Figure 10-62c, the distance ED is too large. Thus, an error was made in this portion of our analysis that represents not only a clue to the proper solution but also the approximate position of our difficulties. Second, returning to Table 10-1, we reexamine the possible dip domains that are associated with two 20-deg ramping thrusts, as there are obvious problems at the back of the structure, in that JI does not coincide with ME. Thus, a problem may exist in this region. The data in Table 10-1 suggest that a −I dip domain can exist between a 0 dip domain and a −II back dip domain of 38 deg. Examining the dip panels on our solution reveals that a −I-deg dip domain was not included in the back part of our solution.
We now backtrack, modifying the first solution by inserting a −I back dip domain between the 0 and −II and the back dip panels (Fig.10-62d). Using Figure 10-40, we know that the distance ED in Figure 10-62c and d should be equal to CB/0.87, and this distance is entered on the figure by measuring down the ramp from point D to E. From the newly calculated position of point E, we construct a newly positioned fault flat. Then, from point E, we project a 0 −I axial surface upward at 100 deg (Table 10-2) to the deformed upper thrust (point K on Fig. 10-62d). This portion of the deformed upper thrust dips at 38 deg, downward from point H (compare Fig. 10-62c to d). From point K, we next project a −I −II axial surface upward at 119 deg (Table 10-2). We can also conclude that to the left of point K exists a 20-deg −I back dip panel and another 0 −I axial surface that intersects the lower decollement at point L (Fig. 10-62d), which is established by projecting the upper fault at a 20-deg dip to the combined lower fault flat. This solution, although only slightly different from Figure 10-62c, creates a deformed horse block and a more reasonable interpretation.
From this complex exercise, we conclude that (1) duplexes produce more rounded structures; (2) structural balancing can be nonunique, even under ideal situations; and (3) the interpretation process can be rigorous, but in this age of global energy economics and price variations, the rewards could be substantial. The better we understand the detailed geometry of structures, the more likely we are to find additional reserves of oil and gas.
Box and Lift-Off Structures
Box and lift-off structures represent a particular class of folds that, when viewed relative to the regional dip, are roughly symmetric but angular structures that contain steeply dipping limbs (Figs. 10-63 and 10-64). Both structural types form along a zone of weak detachment located at depth and possess the characteristic that the decollement is isoclinally folded into the hanging wall (Laubscher 1961; Namson 1981). In the Jura Mountains, this zone of weakness consists of evaporites (i.e., gypsum), although overpressured shales are likely to produce a similar deformational style. Box and lift-off structures differ from diapiric structures in that there is less mass transport or flow into the cores of these folds. This causes the box and lift-off structures to have almost vertically dipping limbs at the lower structural level. In addition, diapiric structures typically result from a gravity instability, whereas box and lift-off folds result from compression.
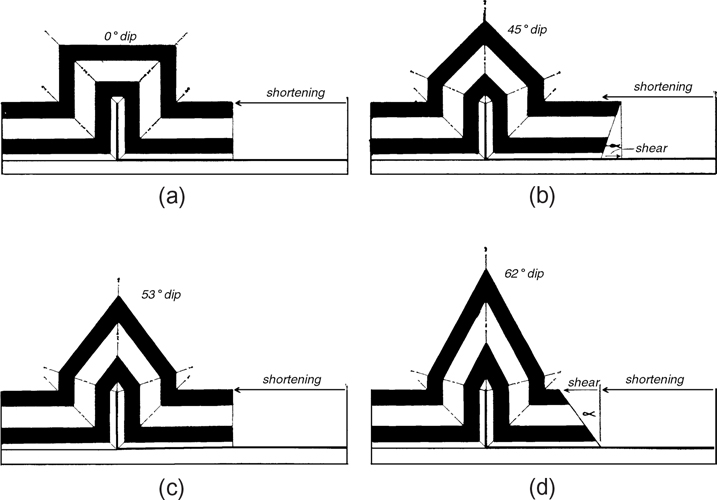
Figure 10-63 (a) Box and (b–d) lift-off structures. (From Namson 1981. Published by permission of the Chinese Petroleum Institute.)
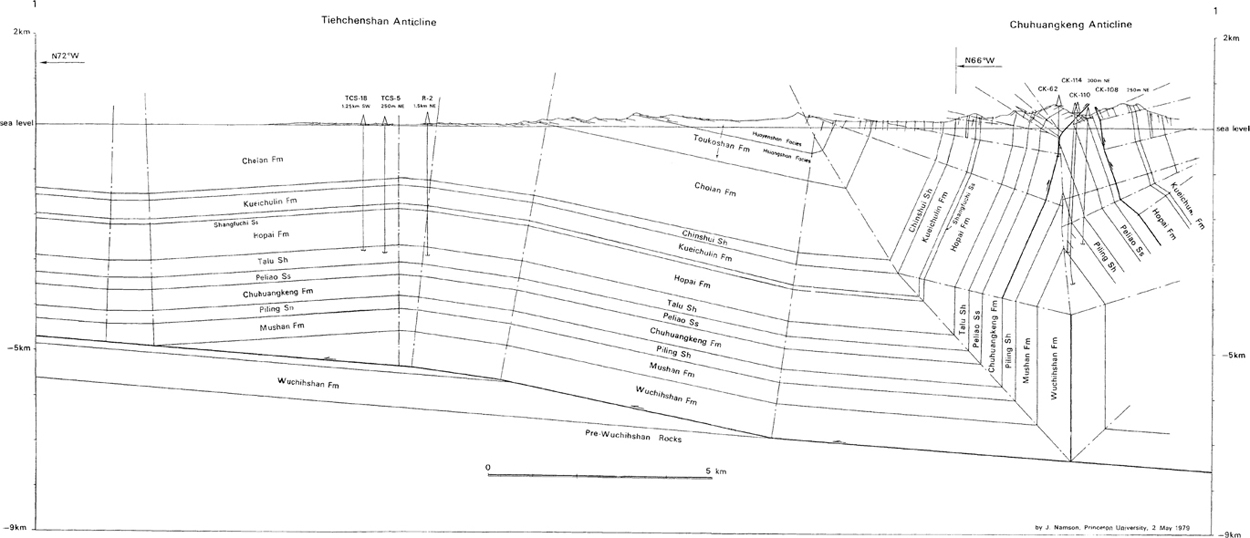
Figure 10-64 Cross section of the Chuhuangkeng Anticline, Taiwan, showing a broad region of near-vertical dips. (From Namson 1981. Published by permission of the Chinese Petroleum Institute.)
The box fold structural style was once thought to be a relatively rare structural style. Today the structures have been observed in many compressional environments and can be productive of hydrocarbons. Box folds can be distinguished from other structural styles in that the width of the box fold, across the crest of the fold, maps as a region of constant width (Fig. 10-63a). No other fold style exhibits this geometry in map view.
Box and lift-off structures can be recognized in outcrop from their bilateral symmetry and also from their angular geometry. If broad zones of vertically dipping beds are encountered in outcrop (e.g., 70 deg to 80 deg), then these structural styles are suspect (Fig. 10-64).
Box folds have nearly flat tops, vertically dipping limbs, and axial surfaces that dip at about 45 deg (Fig. 10-63a). If in a region of vertically dipping beds two axial surfaces intersect at nearly right angles, then you should consider the possibility that box folds are present. On seismic sections, vertically dipping beds do not image, and thus a pattern of gently dipping reflectors separated by two zones of noncoherent reflectors, representing the almost vertically dipping beds, may be an indication of this style of deformation. However, zones of noncoherent reflectors on seismic sections can result from other causes, such as strike-slip faulting, rock type, or data acquisition problems. Seismic reflection analysis (Payton 1977; Sheriff 1980) could resolve the correlation problem because the sedimentary sequences on the flanks of box and lift-off folds are elevated within the cores of these structures.
Lift-off folds differ from box folds in that the shallow limbs of the lift-off fold style tend to dip in the 45-deg to 62-deg range relative to the regional dip. At depth, the shallow, steeply dipping limbs merge into a zone of nearly vertical-dipping limbs (Fig. 10-63). If you observe nearly vertical beds just above a decollement, it may be impossible to determine whether you are observing a lift-off or box fold, as both structural types possess 45-deg dipping axial surfaces on this structural level. In practice, however, this difference may be academic.
If the lift-off fold is not subject to bedding plane shear, then the limbs of the fold at a higher structural level dip at about 53 deg (Fig. 10-63b). This dip angle changes with increasing bedding plane shear (Namson 1981), and the amount of shear can be calculated from the dip of the fold limbs (Mitra and Namson 1989). If there is bedding plane shear within the structure, then Mitra and Namson (1989) show that this shear affects the depth to detachment (as presented in the section Depth-to-Detachment Calculations in this chapter). However, the difference is not major for small amounts of shear. Mitra and Namson (1989) should be consulted for more accurate depth-to-detachment calculations.
Box and lift-off folds are commonly found in association with each other. In the Prealps, Mosar and Suppe (1988) observed that lift-off structures form in the leading or the trailing position relative to fault propagation folds. In addition, they observed that fault propagation folds may transform laterally into lift-off structures and that the two structural styles may be related to each other as the local cutoff angle steepens. Thus, at low cutoff angles (less than about 18 deg to 20 deg), fault bend folds may form in an area, whereas if the cutoff angle is greater than about 20 deg to 25 deg, fault propagation folds usually form instead of fault bend folds. If the cutoff angle increases to over 60 deg along the strike of a structure, then the structure may transform into a lift-off or box fold.
When mapping box or lift-off structures, apply the kink method in your mapping. When applying this method to these symmetric structures, remember that the hanging wall decollement is assumed to rise vertically above the basal detachment and to fold back upon itself (Figs. 10-63 and 10-64). Box folds can be distinguished from other structural styles in that the width of the box fold, across the crest of the fold, maps as a region of constant width (Fig. 10-63). No other fold style exhibits this geometry in map view.
Triangle Zones and Wedge Structures
Triangle zones and wedge structures are complex structures that exhibit both a lower and an upper detachment. The basal detachment is often called the sole thrust, or floor thrust, whereas the uppermost thrust is called the roof thrust (Fig. 10-65) (Boyer and Elliott 1982). In the case of triangle zones, the roof thrust is a passive back thrust. The wedge moves above the sole thrust and beneath the roof thrust, peeling off the shallow portions of the cover.
Figure 10-65 Simple triangle zone with passive roof backthrust.
Gordy and Frey (1975) and Gordy et al. (1977) initially used the concept of a triangle zone to explain the complex relationships associated with an anticlinorium located at the front of the Canadian Rockies. Jones (1982) refined the concept and showed that the structure contained a duplex and that it was responsible for the termination of the eastern-directed thrusting along the Rocky Mountain thrust front. We have learned that during the orogenic process, the deformation progresses (advances) toward the foreland. Therefore, a frontal portion that existed at a previous time during the formation of the thrust belt would exist today hinterland of the thrust front. This implies that fossil triangle zones can exist within the cores of mountain ranges, perhaps representing the frontal edge of the deformation at a previous time.
A simple triangle zone that uses the concept of a ramping monocline is illustrated in Figure 10-65. Notice that the deformation terminates where the roof thrust meets the sole thrust, creating a half-syncline. This monoclinally shaped syncline with only one limb lies foreland of the thrust belt. Jones (1982) mapped a half-syncline along the Rocky Mountain front and concluded that a wedge-shaped body of material must be thrust underneath the dipping beds of the half-syncline. For an explanation of the details of the complex structure of triangle zones, consult Sterne (2006).
A seismic section of a complex triangle zone is imaged in Figure. 10-66. Notice the wedge-shaped body represented by the duplication of the reflection located between sp 190 to sp 240 and at 1.2 sec to 1.5 sec. That reflection appears to correlate to the flat reflection at 1.5 sec in front of the structure. On the seismic line, use the following procedures to locate the backthrust. First, project the synclinal axial surface at the front of the triangle zone downward to where the axial surface intersects the sole thrust, as in Figure 10-66. At the point where the two surfaces intersect, construct a line that is parallel to the monoclinally dipping beds. Project this line that represents the backthrust toward the surface. The backthrust conforms to the shape of the hanging wall beds. Notice at sp 220 and at 1000 ms how the backthrust separates dipping beds in its hanging wall from flatter beds in the footwall. This change in bed dips across the backthrust is indicative of a decollement or faulting.

Figure 10-66 Seismic section imaging a triangle zone to the right of sp 250, Raton Basin, Colorado. (After Applegate and Rose 1985 in Gries and Dyer 1985. Published by permission of the Rocky Mountain Association of Geologists and the Denver Geophysical Society.)
Medwedeff (1988, 1989) extends the concept of interactive sole and roof thrusts to single structures, and he calls these interactive thrusts wedge structures. Figure 10-67a is an example of an incipient wedge structure that has two bends on its sole thrust and a single bend in its roof thrust. As the deformation progresses (Fig. 10-67b), motion along the sole thrust deforms the roof thrust. Back and frontal dip panels form over what is essentially a fault bend fold that also has an upper roof detachment. Notice, however, that the overlying beds in effect ride up the roof thrust, and they will also form fold panels above the upper detachment. This structurally higher fold is caused by the bends in the roof thrust, so its dip panels terminate at the upper detachment (Fig. 10-67b). The result is two folds for the price of one, which are slightly offset from each other. As the deformation progresses (Fig. 10-67c), the axial surfaces interfere and annihilate each other as they form branch points. This example illustrates that the deformation process can be very transient and that the introduction of additional fault bends results in folds that have more rounded tops (Fig. 10-67c).

Figure 10-67 (a)–(c) Wedge structure showing progressive stages of development. (Published by permission of Don Medwedeff 1988.)
Medwedeff (1988) also uses wedge structures to model the complex stratigraphic relationships present at Wheeler Ridge, California. The restored structure and the present structure, with the corresponding positions of the wells (with their well logs), are shown in Figures 10-68 and 10-69 respectively. These figures demonstrate how well logs can be used to define the complex relationships that exist within some structures. Precise correlations and balancing can be effectively integrated to locate prospects that may not be recognized by normal mapping techniques.
Figure 10-68 Wedge structure in its initial, or restored, state as defined by well logs; Wheeler Ridge, California, USA. (Published by permission of Don Medwedeff 1988.)

Figure 10-69 Wedge structure in its present state as defined by well logs, Wheeler Ridge, California, USA. (Published by permission of Don Medwedeff 1988.)
Interference Structures
Would you believe that anticlines can form over synclines with no evidence of an intervening fault or evidence of more than one deformation? Nevertheless, clear evidence for this seemingly contradictory relationship can be seen on seismic sections and in outcrops. In the previous section on wedge structures, we saw that deformation on a lower level can modify the shape and the form of dip panels of structures located on a higher structural level. Where structural modification of this type results from a single deformation along one thrust surface, as illustrated in Figure 10-70a, the resulting structures are called interference structures (Suppe 1988).
Interference structures are commonly present where the spacing between ramps is relatively narrow, causing the back dip panel of the leading structure to interfere with the frontal dip panel of the trailing structure (Fig. 10-70a and b). The interference tends to produce chevron folds and conjugate kink structures (Weiss 1972; Suppe 1988).
The resulting interference patterns that are created by the deformation are dependent on ramp spacing, initial cutoff angle, and the total amount of slip. Two model patterns are useful in mapping these types of structures, although this does not deny the usefulness of other types of patterns. In the first example, the leading fault bend fold has run up a ramp and the frontal dip panel of the trailing fold (a monocline) occupies a portion of the lower flat (Fig. 10-70a). The resulting deformation creates a structure in which a frontal fold lies beneath a structurally higher anticline formed by the trailing fold. Flat dips and a syncline exist just above the lower flat, directly in front of the trailing monocline.
As the deformation progresses, the frontal portions of the trailing monocline will start to run up the leading ramp (Fig. 10-70b). If both ramps have about the same cutoff angle, then as the trailing monocline runs up the second ramp, the beds in the frontal dip panel of the trailing monocline will flatten. One result of the deformation is to create a region of nearly flat dips and a narrow syncline over the leading ramp as the monocline unfolds. This example once again stresses the progressive nature of the deformation. Structures were not cast in their present-day positions; they move, and thus strata bend and rebend. Knowledge of which regions of a fold have been subject to refolding should aid in the prediction of fracture porosities and better well site locations, which can result in greater productivity. In our example, some of the strata in the back dip panel of the leading fault bend fold were first bent backward, and then forward, by the advancing monocline. As the active axial surfaces sweep through the structure, particular regions within these folds will be subject to repeated deformation and bending that enhances fracture porosity. One can study the refolding by applying the kink method and by modeling increasing amounts of slip into the structure to study how the deformation progresses.
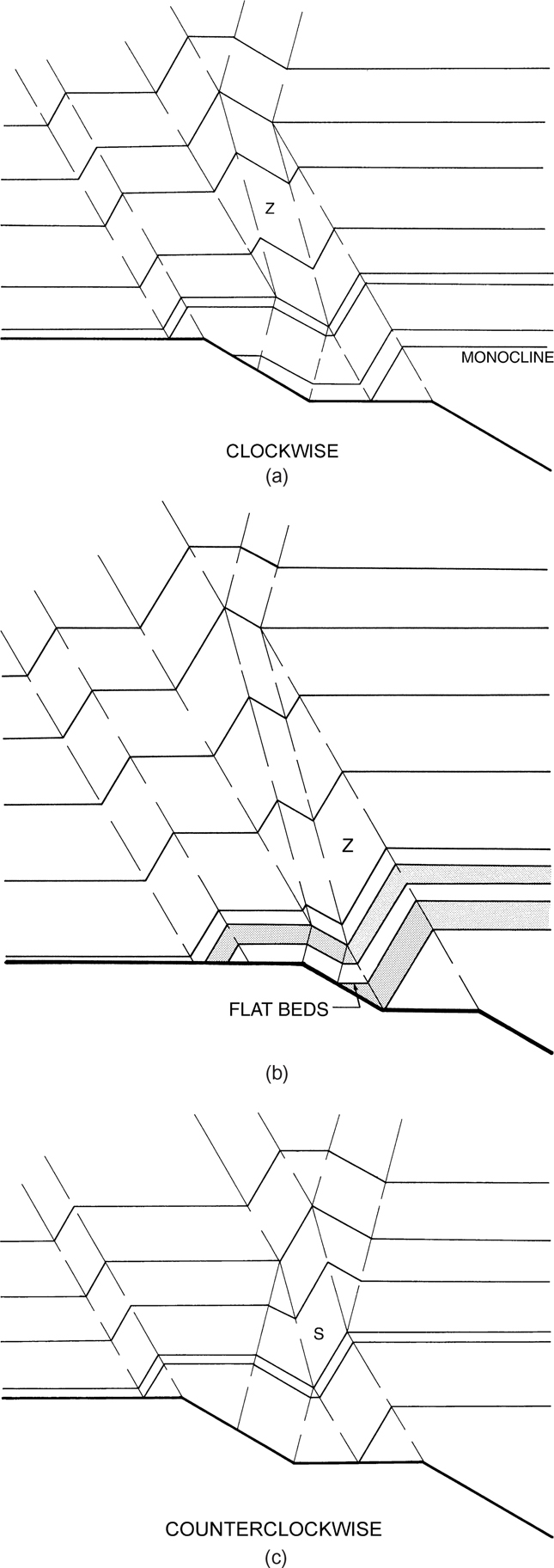
Figure 10-70 Interference structures (a) and (b) for clockwise deformation and increasing slip (c) for counterclockwise shear. (Modified after Suppe 1988. Published by permission of John Suppe.)
We make two more points before leaving this subject. First, as the initial cutoff angle decreases, the structurally higher anticline will move vertically away from the structurally lower syncline, but at the same time shift to a position where it is located almost directly above the syncline. Second, the two examples presented here are for a clockwise shear within the interfering frontal and back dip panels. In other words, the beds within the interfering dip panels exhibit a Z vergence (Suppe 1988). An example of an S vergence (counterclockwise shear), in which the frontal dip panel of the trailing monocline passes through the upper anticline, is shown in Figure 10-70c.
