Appendix E. Homogeneous Coordinates and Transformation Matrices
This appendix presents a brief discussion of homogeneous coordinates, stated in a different way from Chapter 5, “Viewing Transformations, Culling, Clipping, and Feedback.” It also summarizes the forms of the transformation matrices used for rotation, scaling, translation, perspective, and orthographic projection discussed in detail in Chapter 5. For a more detailed discussion on projection, see The Real Projective Plane, by H. S. M. Coxeter, 3rd ed. (Springer, 1992). To see how to use the library accompanying this book, see Chapter 5.
In the discussion that follows, the term homogeneous coordinates always means three-dimensional homogeneous coordinates, although projective geometries exist for all dimensions.
This appendix has the following major sections:
Homogeneous Coordinates
OpenGL commands usually deal with two- and three-dimensional vertices, but in fact all are treated internally as three-dimensional homogeneous vertices comprising four coordinates. Every column vector
(which we write as (x, y, z, w)T) represents a homogeneous vertex if at least one of its elements is nonzero. If the real number a is nonzero, (x, y, z, w)T and (ax, ay, az, aw)T represent the same homogeneous vertex. (This is just like fractions: x/y = (ax)/(ay).) A three-dimensional Euclidean space point (x, y, z)T becomes the homogeneous vertex with coordinates (x, y, z, 1.0)T, and the two-dimensional Euclidean point (x, y)T becomes (x, y,0.0, 1.0)T.
As long as w is nonzero, the homogeneous vertex (x, y, z, w)T corresponds to the three-dimensional point (x/w, y/w, z/w)T. If w = 0.0, it corresponds to no Euclidean point, but to some idealized “point at infinity.” To understand this point at infinity, consider the point (1, 2, 0, 0), and note that the sequence of points (1, 2, 0, 1), (1, 2, 0, 0.01), and (1, 2.0, 0.0, 0.0001) corresponds to the Euclidean points (1, 2), (100, 200), and (10, 000, 20, 000). This sequence represents points rapidly moving toward infinity along the line 2x = y. Thus, you can think of (1, 2, 0, 0) as the point at infinity in the direction of that line.
OpenGL might not handle homogeneous clip coordinates with w < 0 correctly. To be sure that your code is portable to all OpenGL systems, use only nonnegative w-values.
Transforming Vertices
Vertex transformations (such as rotations, translations, scaling, and shearing) and projections (such as perspective and orthographic) can all be represented by applying an appropriate 4 × 4 matrix to the coordinates representing the vertex. If v represents a homogeneous vertex and M is a 4 × 4 transformation matrix, Mv is the image of v under the transformation by M. (In computer-graphics applications, the transformations used are usually nonsingular. In other words, the matrix M can be inverted. This isn’t required, but some problems arise with singular matrices.)
After transformation, all transformed vertices are clipped so that x, y, and z are in the range [–w, w] (assuming w > 0). Note that this range corresponds in Euclidean space to [–1.0, 1.0].
Transforming Normals
Normal vectors aren’t transformed in the same way that vertices or position vectors are. Mathematically, it’s better to think of normal vectors not as vectors, but as planes perpendicular to those vectors. Then the transformation rules for normal vectors are described by the transformation rules for perpendicular planes.
A homogeneous plane is denoted by the row vector (a, b, c, d), where at least one of a, b, c, and d is nonzero. If q is a nonzero real number, (a, b, c, d) and (qa, qb, qc, qd) represent the same plane. A point (x, y, z, w)T is on the plane (a, b, c, d) if ax + by + cz + dw = 0. (If w = 1, this is the standard description of a Euclidean plane.) In order for (a, b, c, d) to represent a Euclidean plane, at least one of a, b, or c must be nonzero. If they’re all zero, (0, 0, 0, d) represents the “plane at infinity,” which contains all the “points at infinity.”
If p is a homogeneous plane and v is a homogeneous vertex, the statement “v lies on plane p” is written mathematically as pv = 0, where pv is normal matrix multiplication. If M is a nonsingular vertex transformation (i.e., a 4 × 4 matrix that has an inverse M–1), pv = 0 is equivalent to pM–1Mv = 0, so Mv lies in the plane pM–1. Thus, pM–1 is the image of the plane under the vertex transformation M.
If you like to think of normal vectors as vectors instead of as the planes perpendicular to them, let v and n be vectors such that v is perpendicular to n. Then nTv = 0. Thus, for an arbitrary nonsingular transformation M, nTM – 1Mv = 0, which means that nTM–1 is the transpose of the transformed normal vector. Thus, the transformed normal vector is M–1T n. In other words, normal vectors are transformed by the inverse transpose of the transformation that transforms points. Whew!
Transformation Matrices
Although any nonsingular matrix M represents a valid projective transformation, a few special matrices are particularly useful. These matrices are listed in the following subsections.
Rotation
Let v = (x, y, z)T, and u = v/||v|| = (x′, y′, z′)T. Also let

and
M = uuT + cos θ(I – uuT) + sin θ S
where

Then
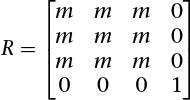
where m represents the elements from M, which is the 3 × 3 matrix defined on the preceding page. The R matrix is always defined. If x = y = z = 0, R is the identity matrix. You can obtain the inverse of R, R–1, by substituting –θ for θ, or by transposition.
Often, you’re rotating about one of the coordinate axes. The corresponding matrices are as follows:
As before, the inverses are obtained by transposition.
Perspective Projection

P is defined as long as l ≠ r, t ≠ b, and n ≠ f.




