14
Sample size

In this chapter we discuss one of the most common decisions in statistical practice: the choice of the sample size for a study. We initially focus on the case in which the decision maker selects a fixed sample size n, collects a sample x₁, ..., x_n, and makes a terminal decision based on the observed sample. Decision-theoretic approaches to sample size determination formally model the view that the value of an experiment depends on the use that is planned for the results, and in particular on the decision that the results must help address. This approach, outlined in greater generality in Chapter 13, provides conceptual and practical guidance for determining an optimal sample size in a very broad variety of experimental situations. Here we begin with an overview of decision-theoretic concepts in sample size. We next move to a general simulation-based algorithm to solve optimal sample size problems in complex practical applications. Finally, we illustrate both theoretical and computational concepts with examples.

The main reading for this chapter is Raiffa and Schlaifer (1961, chapter 5), who are generally credited for providing the first complete formalization of Bayesian decision-theoretic approaches to sample size determination. The general ideas are implicit in earlier decision-theoretic approaches. For example Blackwell and Girshick (1954, page 170) briefly defined the framework for Bayesian optimal fixed sample size determination.

Featured book (Chapter 5):

Raiffa, H. and Schlaifer, R. (1961). Applied Statistical Decision Theory, Harvard University Press, Boston, MA.

Textbook references on Bayesian optimal sample sizes include DeGroot (1970) and Berger (1985). For a review of Bayesian approaches to sample size determination (including less formal decision-theoretic approaches) see Pham-Gia and Turkkan (1992), Adcock (1997), and Lindley (1997); for practical applications see, for instance, Yao et al. (1996) and Tan and Smith (1998).

14.1 Decision-theoretic approaches to sample size

14.1.1 Sample size and power

From a historical perspective, a useful starting point for understanding decision-theoretic sample size determination is the Neyman–Pearson theory of testing a simple hypothesis against testing a simple alternative (Neyman and Pearson 1933). A standard approach in this context is to seek the smallest sample size that is sufficient to achieve a desired power at a specified significance level. From the standpoint of our discussion, there are three key features in this procedure:

1. After the data are observed, an optimal decision rule—in this case the use of a uniformly most powerful test—is used.

2. The sample size is chosen to be the smallest that achieves a desired performance level.

3. The same optimality criteria—in this case significance and power—are used for selecting both a terminal decision rule and the sample size.

As in the value of information analysis of Chapter 13, the sample size depends on the benefit expected from the data after it will be put to use, and the quantification of this benefit is user specified. This structure foreshadows the decision-theoretic approach to sample size that was to be developed in later years in the influential work by Wald (1947b), described below.

Generally, in choosing the sample size for a study, one tries to weigh the trade-off between carrying out a small study and improving the final decision with respect to some criterion. This can be achieved in two ways: either by finding the smallest sample size that guarantees a desired level of the criterion, or by explicitly modeling the trade-off between the utilities and costs of experimentation. Both of these approaches are developed in more detail in the remainder of this section.

14.1.2 Sample size as a decision problem

In previous chapters we dealt with problems where a decision maker has a utility u(a(θ)) for decision a when the state of nature is θ. In the statistical decision-theoretic material we also cast the same problem in terms of a loss L(θ, a) for making decision a when the state of nature is θ, and the decision is based on a sample xⁿ = (x₁, x₂, ..., x_n) of size n drawn from f (x|θ). We now extend this to also choosing optimally the sample size n of the experiment. We first specify a more general detailed function u(θ, a, n) or, equivalently, a loss function L(θ, a, n) for observing a sample of size n and making decision a when the state of nature is θ. The sample size n is really an action here, so the concepts of utility and loss are not altered in substance. We commonly use the form

The function L(θ, a) in (14.2) refers, as in previous chapters, to the choice of a after the sample is observed and is referred to as the terminal loss function. The function C(n) represents the cost of collecting a sample of size n. This formulation can be traced to Wald (1947a) and Wald (1949).

The practical implications of accounting for the costs of experimentation in (14.2) is explained in an early paper by Grundy et al.:

Similar considerations apply to a broad range of other scientific contexts. Raiffa and Schlaifer further comment on the assumption of additivity of the terminal utility u(a(θ)) and experimental costs C(n):

14.1.3 Bayes and minimax optimal sample size

A Bayesian optimal sample size can be determined for any problem by specifying four components: (a) a likelihood function for the experiment; (b) a prior distribution on the unknown parameters; (c) a loss (or utility) function for the terminal decision problem; and (d) a cost of experimentation. Advantages include explicit consideration of costs and benefits, formal quantification of parameter uncertainty, and consistent treatment of this uncertainty in the design and inference stages.

Specifically, say π represents a priori knowledge about the unknown parameters, and is the Bayes rule with respect to that prior (see Raiffa and Schlaifer 1961, or DeGroot 1970). As a quick reminder, the Bayes risk is defined, as in equation (7.9), by

and the Bayes rule minimizes the Bayes risk r(π, δ_n) among all the possible δ_n when the sample size is n. Thus the optimal Bayesian sample size n* is the one that minimizes

By expanding the definition of the risk function and reversing the order of integration, we see that

Similarly, the Bayesian formulation can be reexpressed in terms of utility as the maximization of the function

Both formulations correspond to the solution of a two-stage decision tree similar to those of Sections 12.3.1 and 13.1.3, in which the first stage is the selection of the sample size, and the second stage is the solution of the statistical decision problem. In this sense Bayesian sample size determination is an example of preposterior analysis. Experimental data are conditioned upon in the inference stage and averaged over in the design stage.

By contrast, in a minimax analysis, we would analyze the data using the minimax decision function chosen so that

Thus the best that one can expect to achieve after a sample of size n is observed is sup_θɛΘ , and the minimax sample size n^M minimizes

Exploiting the formal similarity between the Bayesian and minimax schemes, Blackwell and Girshick (1954, page 170) suggest a general formalism for the optimal sample size problem as the minimization of a function of the form

where δ_n is a terminal decision rule based on n observations. This formulation encompasses both frequentist and Bayesian decision-theoretic approaches. In the Bayesian case δ_n is replaced by . For the minimax case, δ_n is the minimax rule, and π the prior that makes the minimax rule a Bayes rule (the so-called least favorable prior), if it exists. This formulation allows us in principle to specify criteria that do not make use of the optimal decision rule in evaluating ρ, a feature that may be useful when seeking approximations.

14.1.4 A minimax paradox

With some notable exceptions (Chernoff and Moses 1959), explicit decision-theoretic approaches are rare among frequentist sample size work, but more common within Bayesian work (Lindley 1997, Tan and Smith 1998, Müller 1999). Within the frequentist framework it is possible to devise sensible ad hoc optimal sample size criteria for specific families of problems, but it is more difficult to formulate a general rationality principle that can reliably handle a broad set of design situations. To illustrate this point consider this example, highlighting a limitation of the minimax approach.

Suppose we are interested in testing H₀ : θ ≤ θ₀ versus H₁ : θ>θ₀ based on observations sampled from N(θ, σ ²), the normal distribution with unknown mean θ and known variance σ ². We can focus on the class of tests that reject the null hypothesis if the sample mean is larger than a cutoff d, , where I_E is the indicator function of the event E. The sample mean is a sufficient statistic and this class is admissible (see Berger 1985 for details).

Let F(.|θ) be the cumulative probability function of given θ. Under the 0–1–k loss function of Table 14.1, the associated risk is given by

Table 14.1 The 0–1–k loss function. No loss is incurred if H₀ holds and action a₀ is chosen, or if H₁ holds and action a₁ is chosen. If H₁ holds and decision a₀ is made, the loss is 1; if H₀ holds and decision a₁ is made, the loss is k.

	H0	H1
a0: accept H0	0	1
a1: reject H0	k	0

Let denote the power function (Lehmann 1983). In the frequentist approach to hypothesis testing, the power function evaluated at θ₀ gives the type I error probability. When evaluated at any given θ = θ₁ chosen within the alternative hypothesis, the power function gives the power of the test against the alternative θ₁.

Since P is increasing in θ, it follows that

which is minimized by choosing d such that kP(θ₀) = 1 – P(θ₀), that is P(θ₀) = 1/(1 + k). When one specifies a type I error probability of α, the implicit k can be determined by solving 1/(1 + k) = α, which implies k = (1 – α)/α.

Solving the equation P(θ₀) = 1/(1 + k) with respect to the cutoff point d, we find a familiar solution:

Since inf_δ∈D sup_θ R(θ, δ) = sup_θ R(θ, δ_dM), δ^M = δ_dM is the minimax rule.

It follows that sup_θ R(θ, δ_dM) + C(n) = k/(k + 1) + C(n) is an increasing function in n, as long as C is itself increasing, which is always to be expected. Thus, the optimal sample size is zero! The reason is that, with the 0–1–k loss function, the minimax risk is constant in θ. The minimax strategy is rational if an intelligent opponent whose gains are our losses is choosing θ. In this problem such an opponent will always choose θ = θ₀ and make it as hard as possible for us to distinguish between the two hypotheses. This is another example of the “ultra-pessimism” discussed in Section 13.4.

Let us now study the problem from a Bayesian viewpoint. Using the 0–1–k loss function, the posterior expected losses of accepting and rejecting the null hypothesis are π(H₁|xⁿ) and kπ(H₀|xⁿ), respectively. The Bayes decision minimizes the posterior expected loss. Thus, the Bayes rule rejects the null hypothesis whenever π(H₁|xⁿ) > k/(1 + k) (see Section 7.5.1). Suppose we have a prior on θ. Solving the previous inequality in , we find that the Bayes decision rule is with the cutoff given by

With a little bit of work, we can show that the Bayes risk r is given by

Figure 14.1 Bayes risk r(π, n) as a function of the sample size n with the 0–1–k loss function. In the left panel the cost per observation is c = 0.001, in the right panel the cost per observation is c = 0.0001. While the optimal sample size is unique in both cases, in the case on the right a broad range of choices of sample size achieve a similar risk.

The above expression can easily be evaluated numerically and optimized with respect to n, as we did in Figure 14.1. While it is possible that the optimal n may be zero if costs are high enough, a range of results can emerge depending on the specific combination of cost, loss, and hyperparameters. For example, if C(n) = cn, with c = 0.001, and if k = 19, σ = 1, and τ₀ = 1, then the optimal sample size is n_B = 54. When the cost per observation c is 0.0001, the optimal sample size is n_B = 255.

14.1.5 Goal sampling

A different Bayesian view of sample size determination can be traced back to Lind-ley’s seminal paper on measuring the value of information, discussed in Chapter 13. There, he suggests that a:

A broad range of frequentist and Bayesian methods for sample size determination can be described as choosing the smallest sample that is sufficient to achieve, in expectation, some set goals of experimentation. An example of the former is seeking the smallest sample size that is sufficient to achieve a desired power at a specified significance level. An example of the latter is seeking the smallest sample size necessary to obtain, in expectation, a fixed width posterior probability interval for a parameter of interest. We refer to this as goal sampling. It can be implemented sequentially, by collecting data until a goal is met, or nonsequentially, by planning a sample that is sufficient to reach the goal in expectation.

Choosing the smallest sample size to achieve a set of goals can be cast in decision-theoretic terms, from both the Bayesian and frequentist viewpoints. This approach can be described as a constrained version of that described in Section 14.1.3, where one sets a desired value of ρ and minimizes (14.7) subject to that constraint. Because both cost and performance are generally monotone in n, an equivalent formulation is to choose the smallest n necessary to achieve a desired ρ. This formulation is especially attractive when cost of experimentation is hard to quantify or when the units of ρ are difficult to compare to the monetary unit c.

In hypothesis testing, we can also use this idea to draw correspondences between Bayesian and classical approaches to sample size determination based on controlling probabilities of classification error. We illustrate this approach in the case of testing a simple hypothesis against a simple alternative with normal data. Additional examples are in Inoue et al. (2005).

Suppose that x₁, ..., x_n is a sample from a N(θ, 1) distribution. It is desired to test H₀ : θ = θ₀ versus H₁ : θ = θ₁, where θ₁ >θ₀, with the 0–1 loss function. This is a special case of the 0–1–k loss of Table 14.1 with k = 1 and assigns a loss of 0 to both correct decisions and a loss of 1 to both incorrect decisions. Assume a priori that π(H₀) = 1 – π(H₁) = π = 1/2. The Bayes rule is to accept H₀ whenever π(H₀|xⁿ) > 1/2 or, equivalently, . Let F(.|θ) denote the cumulative probability function of given θ. Under the 0–1 loss function, the Bayes risk is

where Φ(z) is the cdf of a standard normal density. The Bayes risk in (14.9) is monotone and approaches 0 as the sample size approaches infinity.

The goal sampling approach is to choose the minimum sample size needed to achieve a desired value of the expected Bayes risk, say r₀. In symbols, we find n_r0 that solves . Applying this to equation (14.9) we obtain

where z_1−r0 is such that (z_1−r0) = 1 – r₀.

A standard frequentist approach to sample size determination corresponds to determining the sample size under specified constraints in terms of probabilities of type I and type II error (see, for example, Desu and Raghavarao 1990, Shuster 1993, Lachin 1998). In our example, the frequentist optimal sample size is given by

where α and β correspond to the error probabilities of type I and II, respectively.

The frequentist approach described above does not make use of an explicit loss function. Lindley notes that:

Although based on different concepts, we can see in this example that classical and Bayesian optimal sample sizes are the same whenever

Inoue et al. (2005) discuss a general framework for investigating the relationship between the two approaches, based on identifying mappings that connect the Bayesian and frequentist inputs necessary to obtain the same sample size, as done in (14.12) for the mapping between the frequentist inputs α and β and the Bayesian input r₀. Their examples illustrate that one can often find correspondences even if the underlying loss or utility functions are different.

Adcock (1997) formalizes goal-based Bayesian methods as those based on setting

and solving for n. Here T(xⁿ) is a test statistic derived from the posterior distribution on the unknowns of interest. It could be, for instance, the posterior probability of a given interval, the length of the 95% highest posterior interval, and so forth. T(xⁿ) plays the role of the posterior expected loss, though direct specification of T bypasses both the formalization of a decision-theoretic model and the associated computing. For specific test statistics, software is available (Pham-Gia and Turkkan 1992, Joseph et al. 1995, and Joseph and Wolfson 1997) to solve sample size problems of the form (14.13).

Lee and Zelen (2000) observe that even in frequentist settings it can be useful to set α and β so that they result in desirable posterior probabilities of the hypothesis being true conditional on the study’s result. Their argument relies on a frequentist analysis of the data, but stresses the importance of (a) using quantities that are conditional on evidence when making terminal decisions, and (b) choosing α and β in a way that reflects the context to which the results are going to be applied. In the specifics of clinical trials, they offer the following considerations:

14.2 Computing

In practice, finding a Bayesian optimal sample size is often too complex for analytic solutions. Here we describe two general computational approaches for Bayesian sample size determination and illustrate them in the context of a relatively simple example. Let x denote the number of successes in a binomial experiment with success probability θ. We want to optimally choose the sample size n of this experiment assuming a priori a mixture of two experts’ opinions as represented by

π(θ) = 0.5 Beta(θ|3, 1) + 0.5 Beta(θ|3, 3).

For the terminal decision problem of estimating θ assume that the loss function is L(θ, a) = |a – θ|. Let denote the Bayes rule, in this case the posterior median (Problem 7.7). Let the sampling cost be 0.0008 per observation, that is C(n) = 0.0008n. The Bayes risk is

This decision problem does not yield an analytical solution. We explore an alternative solution that is based on Monte Carlo simulation (Robert and Casella 1999). A straightforward implementation of Monte Carlo integration to evaluate (14.14) is as follows. Select a grid of plausible values of n, and a simulation size I.

1. For each n, draw (θ_i, x_i) for i = 1, ..., I. This can be done by generating θ_i from the prior and then, conditionally on θ_i, generating x_i from the likelihood.

2. Compute l_i = L(θ_i, δ*(x_i)) + C(n).

3. Compute .

4. Numerically minimize 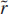with respect to n.

This is predicated on the availability of a closed form for . When that is not the case things become more complicated, but other Monte Carlo schemes are available.

In practice the true r can be slow varying and smooth in n, while can be subject to residual noise from step 3, unless I is very large. Müller and Parmigiani (1995) discuss an alternative computational strategy that exploits the smoothness of r by considering a Monte Carlo sample over the whole design space, and then fit a curve for the Bayes risk r(π, n) as a function of n. The optimization problem can then be solved in a deterministic way by minimization of the fitted curve. In the context of sample size determination, the procedure can be implemented as follows:

1. Select i points n_i, i = 1, ...., I, possibly including duplications.

2. Draw (θ_i, x_i)for i = 1, ..., I. This can be done by generating θ_i from the prior and then x_i from the likelihood.

3. Compute l_i = L(θ_i, δ*(x_i)) + C(n_i).

4. Fit a smooth curve to the resulting points (n_i, l_i).

5. Evaluate deterministically the minimum of .

This effectively eliminates the loop over n implied by step 1 of the previous method. This strategy can also be applied when L is a function of n and when C is a function of x and θ.

To illustrate we choose the simulation points n_i to be integers chosen uniformly in the range (0, 120). The Monte Carlo sample size is I = 200. Figure 14.2(a) shows the simulated pairs (n_i, l_i). We fitted the generated data points by a nonlinear regression of the form

where the values of a and b are estimated based on the Monte Carlo sample. This curve incorporates information regarding (i) the sampling cost; (ii) the value of the expected payoff when no observations are taken, which can be computed easily and is 0.1929; and (iii) the rate of convergence of the expected absolute error to zero, assumed here to be polynomial. The results are illustrated in Figure 14.2(a). Observe that even with a small Monte Carlo sample there is enough information to make a satisfactory sample size choice.

The regression model (14.15) is simple and has the advantage that it yields a closed form solution for the approximate optimal sample size, given by

The sample shown gives . More flexible model specifications may be preferable in other applications.

In this example, we can also rewrite the risk as

Figure 14.2 Monte Carlo estimation of the Bayes risk curve. The points in panel (a) have coordinates (n_i, l_i). The lines show using 200 replicates (dotted) and 2000 replicates (solid). The points in panel (b) have coordinates (n_i, ). The dashed line shows .

where m is the marginal distribution of the data and π_x is the posterior distribution of θ, that is a mixture of beta densities. Using the incomplete beta function, the inner integral can be evaluated directly. We denote the inner integral as when (n_i, x_i) is selected. We can now interpolate directly the points (n_i, ), with substantial reduction of the variability around the fitted curve. This is clearly recommendable whenever possible. The resulting estimated curve is shown in Figure 14.2(b). The new estimate is , not far from the previous approach, which performs quite well in this case.

Figure 14.3 Estimation of the Bayes risk curve under quadratic error loss. Small points are the sampled values of (δ*(x) – θ)² + cn, where δ*(x) denotes the posterior mean. Large points are the posterior variances. The solid line is the fit to the posterior variances.

We end this section by considering two alternative decision problems. The first is an estimation problem with squared error loss L(θ, a) = (θ – a)². Here the optimal terminal decision rule is the posterior mean and the posterior expected loss is the posterior variance (see Section 7.6.1). Both of these can be evaluated easily, which allows us to validate the Monte Carlo approach. Figure 14.3 illustrates the results. The regression model is that of equation (14.15).

The last problem is the estimation of the expected information V(ɛ⁽n)). We can proceed as before by defining

and using curve fitting to estimate the expectation of v_i as a function of n. In this example we choose to use a loess (Cleveland and Grosse 1991) fit for the simulated points. Figure 14.4 illustrates various aspects of the simulation. The top panel nicely illustrates the decreasing marginal returns of experimentation implied by Theorem 13.8. The middle panel shows the change in utility as a function of the prior, and illustrates how the most useful experiments are those generated by parameter values that have low a priori probability, as these can radically change one’s state of knowledge.

Figure 14.4 Estimation of the expected information curve. Panel (a) shows the difference between log posterior and log prior for a sample of θ, x, n. Panel (b) shows the difference between log posterior and log prior versus the log prior. For parameters corresponding to higher values of the log prior, the experiment is less informative, as expected. The points are a low-dimensional projection of what is close to a three-dimensional surface. Panel (c) shows the log of the posterior versus the sample size and number of successes x. The only source of variability is the value of θ.

14.3 Examples

In this section we discuss in detail five different examples. The first four have analytic solutions while the last one makes use of the computational approach of Section 14.2.

14.3.1 Point estimation with quadratic loss

We begin with a simple estimation problem in which preposterior calculations are easy, the solution is in closed form, and it provides a somewhat surprising insight.

Assume that x₁, ... x_n are conditionally independent N(θ, σ ²), with σ ² known. The terminal decision is to estimate θ with quadratic loss function L(θ, a, n) = (θ – a)² + C(n). The prior distribution on θ is , with μ₀ and known.

Since , the posterior distribution of θ given the observed sample mean is where, as in Appendix A.4,

The posterior expected loss, not including the cost of observation, is . Because this depends on the data only via the sample size n but is independent of , we have

If each additional observation costs a fixed amount c, that is C(n) = c n, replacing n with a continuous variable and taking derivatives we get that the approximate optimal sample size is

Considering the two integer values next to n* and choosing the one with the smallest Bayes risk gives the optimal solution, because this function is convex. Figure 14.5 shows this optimization problem when , in which case the optimal sample size is .

In equation (14.20), the optimal sample size is a function of two ratios: the ratio of experimental standard deviation to cost that characterize the cost-effectiveness of a single sample point; and the ratio of experimental variance to prior variance that characterizes the incremental value of each observation in terms of knowledge. As a result, the optimal sample size increases with the prior variance, because less is known a priori, and decreases with cost. However, n* is not a monotone function of the sampling variance σ². When σ² is very small few observations suffice; when it is large, observations lose cost-effectiveness and a smaller overall size is optimal. The largest sample sizes obtain for intermediate values of σ². In particular n*, as a function of σ, is maximized at .

Figure 14.5 Risk functions and components in the optimal sample size problem of Section 14.3.1, when is large compared to σ².

14.3.2 Composite hypothesis testing

Assume again that x₁, ..., x_n is a sample from a N(θ, σ ²) population with σ² known, and that we are now interested in testing H₀ : θ ≤ 0 versus H₁ : θ > 0. As usual, let a_i denote the decision of accepting hypothesis H_i, i = 0, 1. While we generally study loss function such as that of Table 14.1, a useful alternative for this decision problem is

This loss function reflects both whether the decision is correct and whether the actual θ is far from 0 if the decision is incorrect. The loss specification is completed by setting L(θ, a, n) = L(θ, a) + C(n). Assume that the prior density of θ is with μ₀ = 0. To determine the optimal sample size we first determine the optimal by minimizing the posterior expected loss L. Then we perform the preposterior analysis by evaluating L at the optimal and averaging the result with respect to the marginal distribution of the data.

The sample mean is sufficient for xⁿ, so and we can handle all calculations by simply considering . The posterior expected losses for a₀ and a₁ are, respectively,

so that the Bayes rule is a₀ whenever

and a₁, otherwise. This inequality can be rewritten in terms of the posterior mean: we choose a₀ whenever

In this example

because μ₀ = 0, so we decide in favor of a₀ (a₁) if < (>)0. In other words, the Bayes rule is

This defines the terminal decision rule, that is the optimal strategy after the data have been observed, as a function of the sample size and sufficient statistic. Now we need to address the decision concerning the sample size. The posterior expected loss associated with the terminal decision is

The Bayes risk for the sample size decision is the cost of experimentation plus the expectation of the expression above with respect to the marginal distribution of . Specifically,

By adding and subtracting and changing the order of integration in the first term we get

Because then . Also, the marginal distribution of the sample mean is . Thus,

and

Figure 14.6 The Bayes risk for the composite hypothesis testing problem.

In particular, if σ ² = 1, , and the cost of a fixed sample of size n is C(n) = 0.01 n then

Figure 14.6 shows r(π, n) as a function of n taken to vary continuously. Among integer values of n the optimal sample size turns out to be 3.

14.3.3 A two-action problem with linear utility

This example is based on Raiffa and Schlaifer (1961). Consider a health care agency, say the WHO, facing the choice between two actions a₀ and a₁, representing, for example, two alternative prevention programs. Both programs have a setup cost for implementation K_i, i = 0, 1, and will benefit a number k_i of individuals. Each individual in either program can expect a benefit of x additional units of utility, for example years of life translated into monetary terms. In the population, the distribution of x is normal with unknown mean θ and known variance σ². The utility to the WHO of implementing each of the two programs is

We will assume that the WHO has the possibility of gathering a sample xⁿ from the population, to assist in the choice of a program, and we are going to study the optimal sample size for this problem. We are going to take a longer route than strictly necessary and first work out in detail both the expected value of perfect information and the expected value of experimental information for varying n. We are then going to optimize the latter assuming that the expected cost sampling is C(n) = cn.

Throughout, we will assume that θ has a priori normal distribution with mean μ₀ and variance . Expressing in terms of the population variance will simplify analytical expressions.

Let θ_b be the “break-even value,” that is the value of θ under which the two programs have the same utility. Solving u(a₀(θ_b)) = u(a₁(θ_b)) leads to

For a given value of θ, the optimal action a_θ is such that

As θ is unknown, a_θ is not implementable.

Before experimentation, the expected utility of action a_i is E[u(a_i(θ))] = K_i + k_iμ₀. Thus, the optimal decision is

As seen in Chapter 13, the conditional value of perfect information for a given value θ is

Using the linear form of the utility function and the fact that

we obtain

In Chapter 13, we saw that the expected value of perfect information is

It follows from (14.26) that

We define the following integrals:

Using the results of Problem 14.5 we obtain

where , , where φ and Φ denote, respectively, the density and the cdf of the standard normal distribution.

We now turn our attention to the situation in which the decision maker performs an experiment ɛ⁽ⁿ⁾, observes a sample xⁿ = (x₁, ..., x_n), and then chooses between a₀ and a₁. The posterior distribution of θ given xⁿ is normal with posterior mean and posterior variance . Thus, the optimal “a posteriori” decision is

Recalling Chapter 13, the value of performing the experiment ɛ⁽ⁿ⁾ and observing xⁿ as compared to no experimentation is given by the conditional value of the sample information, or observed information, V_xⁿ (ɛ⁽ⁿ⁾). The expectation of it taken with respect to the marginal distribution of xⁿ is the expected value of sample information, or expected information.

In this problem, because the terminal utility function is linear in θ, the observed information is functionally similar to the conditional value of perfect information; that is, the observed information is

One can check that the expected information is V(ɛ⁽ⁿ⁾) = E_μx(V_xⁿ (ɛ⁽ⁿ⁾)). This expectation is taken with respect to the distribution of μ_x, that is a normal with mean μ₀ and variance σ²/n_x where

Following steps similar to those used in the calculation of (14.30), it can be shown that the expected information is

where .

The expected net gain of an experiment that consists of observing a sample of size n is therefore

Let , q = n/n₀, and . The “dimension-less net gain” is defined by Raiffa and Schlaifer (1961) as

To solve the sample size problem we can equivalently maximize g with respect to q and then translate the result in terms of n. Assuming q to be a continuous variable and taking the first- and second-order derivatives of g with respect to q gives

The first-order condition for a local maximum is that g(d, q, z₀) = 0. The function g always admits a local maximum when z₀ = 0. However, when z₀ > 0 a local maximum may or may not exist (see Problem 14.6).

By solving the equation g(d, q, z₀) = 0 we obtain

The large-q approximate solution is then . The implied sample size is

14.3.4 Lindley information for exponential data

As seen in Chapter 13, if the data to be collected are exchangeable, then the expected information I(ɛ⁽ⁿ⁾) is increasing and convex in n. If, in addition to this, the cost of observation is also an increasing function in n, and information and cost are additive, then there are at most two (adjacent) solutions. We illustrate this using the following example taken from Parmigiani and Berry (1994).

Consider exponential survival data with unknown failure rate θ and conjugate prior Gamma(α₀, β₀). Here α₀ can be interpreted as the number of events in a hypothetical prior study, while β₀ can be interpreted as the total time at risk in that study. Let be the total survival time. The expected information in a sample of size n is

This integration is a bit tedious but can be worked out in terms of the gamma function Γ and the digamma function ψ as

The result depends on the number of prior events α₀ but not on the prior total time at risk β₀.

From (14.38), the expected information for one observation is

In particular, if α₀ = 1, then I(ɛ⁽¹⁾) = 1 – C = 0.4288, where C is Euler’s constant. Using a first-order Stirling approximation we get

and

Applying these to the expression of the expected information gives

where .

Using this approximation and taking n to be continuous, when the sampling cost per observation is c (in information units), the optimal fixed sample size is

The optimal solution depends inversely on the cost and linearly on the prior sample size.

14.3.5 Multicenter clinical trials

In a multicenter clinical trial, the same treatment is carried out on different populations of patients at different institutions or locations (centers). The goals of multicenter trials are to accrue patients faster than would be possible at a single center, and to collect evidence that is more generalizable, because it is less prone to center-specific factors that may affect the conclusions. Multicenter clinical trials are usually more expensive and difficult to perform than single-center trials. From the standpoint of sample size determination, two related questions arise: the appropriate number of centers and the sample size in each center. In this section we illustrate a decision-theoretic approach to the joint determination of these two sample sizes using Bayesian hierarchical modeling. Our discussion follows Parmigiani and Berry (1994).

Consider a simple situation in which each individual in the trial receives an experimental treatment for which there is no current alternative, and we record a binary outcome, representing successful recovery. Within each center i, we will assume that patients are exchangeable with an unknown success probability θ_i that is allowed to vary from center to center as a result of differences in the local populations, in the modalities of implementation of care, and in other factors. In a hierarchical model (Stangl 1995, Gelman et al. 1995), the variability of the center-specific parameters θ_i is described by a further probability distribution, which we assume here to be a Beta(α, β) where α and β are now unknown. The θ_i are conditionally independent draws from this distribution, implying that we have no a priori reasons to suppose that any of the centers may have a higher propensity to success. The problem specification is completed by a prior distribution π(α, β) on (α, β).

To proceed, we assume that the number of patients in each center is the same, that is n. Let k denote the number of centers in the study. Because the treatment would eventually be applied to the population at large, our objective will be to learn about the general population of centers rather than about any specific center. This learning is captured by the posterior distribution of α and β. Thus we will optimally design the pair (n, k) to maximize the expected information I on α and β. Alternatively, one could include explicit consideration of one or more specific centers. See for example, Mukhopadhyay and Stangl (1993).

Let x be a k-dimensional vector representing the number of successes in each center. The marginal distribution of the data is

and

where B is the beta function.

The following results consider a prior distribution on α and β given by independent and identically distributed gamma distributions with shape 6 and rate 2, corresponding to relatively little initial knowledge about the population of centers. This prior distribution is graphed in Figure 14.7(a). The implied prior predictive distribution on the probability of success in a hypothetical new center k + 1, randomly drawn from the population of centers, is shown in Figure 14.7(b).

Figure 14.8 shows the posterior distributions obtained by three different allocations of 16 patients: all in one center (n = 16, k = 1), four in each of four centers (n = 4, k = 4), and all in different centers (n = 1, k = 16). All three posteriors are based on a total of 12 observed successes. As centers are exchangeable, the posterior distribution does not depend on the order of the elements of x. So for k = 1 and k = 16 the posterior graphed is the only one arising from 12 successes. For k = 4the posterior shown is one of six possible.

Higher values of the number of centers k correspond to more concentrated posterior distributions; that is, to a sharper knowledge of the population of centers. A different way of illustrating the same point is to graph the marginal predictive distribution of the success probability θ_k+1 in a hypothetical future center, for the three scenarios considered. This is shown in Figure 14.9.

Using the computational approach described in Section 14.2 and approximating k and n by real variables, we estimated the surface I(ɛ^(n,k)). Figure 14.10 gives the contours of the surface. Choices that have the same total number kn of patients are represented by dotted lines. The expected information increases if one increases k and decreases n so that kn remains fixed.

If each patient, in information units, costs a fixed amount c, and if there is a fixed “startup” cost s in each center, the expected utility function is

U_π(n,k) = I(ɛ^(n,k)) – cnk – sk.

For example, assume s = 0.045 and c = 0.015. A contour plot of the utility surface is shown in Figure 14.11. This can be used to identify the optimum, in this case the pair (n = 11, k = 6).

More generally, the entire utility surface provides useful information for planning the study. In practice, planning complex studies will require informal consideration of a variety of constraints and factors that are difficult to quantify in a decision-theoretic fashion. Examining the utility surface, we can divide the decision space into regions with positive and negative utility. In this example, some choices of k and n have negative expected utility and are therefore worse than no sampling. In particular, all designs with only one center (the horizontal line at k = 1) are worse than no experimentation. We can also identify regions that are, say, within 10% of the utility of the maximum. This parallels the notion of credible intervals and provides information on robustness of optimal choices.

Figure 14.7 Prior distributions. Panel (a), prior distribution on α and β. Panel (b), prior predictive distribution of the success probability in center k + 1. Figure from Parmigiani and Berry (1994).

Figure 14.8 Posterior distributions on α and β under alternative designs; all are based on 12 successes in 10 patients. Figure from Parmigiani and Berry (1994).

Figure 14.9 Marginal distributions of the success probability θ_k+1 under alternative designs; all are based on 12 successes in 16 patients. Outcomes are as in Figure 14.8. Figure from Parmigiani and Berry (1994).

Figure 14.10 Contour plot of the estimated information surface as a function of the number of centers k and the number of patients per center n; dotted lines identify designs with the same number of patients, respectively 10, 25, and 50. Figure from Parmigiani and Berry (1994).

Figure 14.11 Contour plot of the estimated utility surface as a function of the number of centers k and the number of patients per center n. Pairs inside the 0-level curve are better than no experimentation. Points outside are worse. Figure from Parmigiani and Berry (1994).

14.4 Exercises

Problem 14.1 A medical laboratory must test N samples of blood to see which have traces of a rare disease. The probability that any individual from the relevant population has the disease is a known θ. Given θ, individuals are independent. Because θ is small it is suggested that the laboratory combine the blood of a individuals into equal-sized pools of n = N/a samples, where a is a divisor of N. Each pool of samples would then be tested to see if it exhibited a trace of the infection. If no trace were found then the individual samples comprising the group would be known to be uninfected. If on the other hand a trace were found in the pooled sample it is then proposed that each of the a samples be tested individually. Discuss finding the optimal a when N = 4, θ = 0.02, and then when N = 300. What can you say about the case in which the disease frequency is an unknown θ?

We work out the known θ case and leave the unknown θ for you. First we assume that N = 4, θ = 0.02, and that it costs $1 to test a sample of blood, whether pooled or unpooled. The possible actions are a = 1, a = 2, and a = 4. The possible experimental outcomes for the pooled samples are:

1. If a = 4 is chosen

   x₄ = 1 Positive test result.

   x₄ = 0 Negative test result.

2. If a = 2 is chosen

   x₂ = 2 Positive test result in both pooled samples.

   x₂ = 1 Positive test result in exactly one of the pooled samples.

   x₂ = 0 Negative test result in both pooled samples.

Recalling that N = 4, θ = 0.02, and that nonoverlapping groups of individuals are also independent, we get

Figure 14.12 presents a simple one-stage decision tree for this problem, solved by using the probabilities just obtained. The best decision is to take one pooled sample of size 4.

Figure 14.12 Decision tree for the pooling example.

Now, let us assume that N = 300. We are going to graph the optimal a for θ as 0.0, 0.1, 0.2, 0.3, 0.4, or 0.5. The cost is still $1. For all a > 1 divisors of N let us define n_a = N/a and x_a the number of subgroups that exhibited a trace of infection. For a = 1 the cost will be N dollars for sure. Therefore, the possible values of x_a are {0, 1, ..., n_a}. Let us also define θ_a as the probability that a particular subgroup exhibits a trace of infection, which is the same as the probability that at least one of the a individuals in that subgroup exhibits a trace of infection. Then

where, again, θ is the probability that a particular individual presents a trace of infection. Finally,

If x_a = 0 then only one test is needed for each group and the cost is C_a = n_a. If x_a = 1, then we need one test for each group, plus a tests for each individual in the specific group that presented a trace of infection. Thus, defining C_a as the cost associated with decision a we have

Also, C_a = n_a + an_a if x_a = n_a. Hence,

E[Ca|θ]	=	na + aE[xa|θ]
	=	na + anaθa
	=	N/a + N[1 – (1 – θ)a]

or, factoring terms,

Table 14.2 gives the values of E[C_a|θ] for all the divisors of N = 300 and for a range of values of θ. Figure 14.13 shows a versus E[C_a|θ] for the six different values of θ. If θ = 0.0 nobody is infected, so we do not need to do anything. If θ = 0.5 it is better to apply the test for every individual instead of pooling them in subgroups. The reason is that θ is high enough that many of the groups will be retested with high probability. Table 14.3 shows the optimal a for each value of θ.

Problem 14.2 Suppose that x₁, x₂, ... are conditionally independent Bernoulli experiments, all with success probability θ. You are interested in estimating θ and your terminal loss function is

Table 14.2 Computation of E[C_a|θ] for different values of θ. The cost associated with optimal solutions is in bold. If θ = 0 no observation is necessary.

θ
a	0.0	0.1	0.2	0.3	0.4	0.5
1	300	300	300	300	300	300
2	150	207	258	303	342	375
3	100	181	246	297	335	362
4	75	178	252	302	336	356
5	60	182	261	309	336	350
6	50	190	271	314	336	345
10	30	225	297	321	328	329
12	25	240	304	320	324	324
15	20	258	309	318	319	319
20	15	278	311	314	314	314
25	12	290	310	311	311	312
30	10	297	309	309	309	310
50	6	304	305	306	306	306
60	5	304	304	305	305	305
75	4	303	304	304	304	304
100	3	302	303	303	303	303
150	2	302	302	302	302	302
300	1	301	301	301	301	301

Figure 14.13 Computation of E[C_a|θ] for different values of θ.

Table 14.3 Optimal decisions for different values of θ.

θ	0.1	0.2	0.3	0.4	0.5
Optimal a	4	3	3	1	1

This is the traditional squared error loss, standardized using the variance of a single observation. With this loss function, errors of the same absolute magnitude are considered worse if they are made near the extremes of the interval (0, 1). You have a Beta(1.5,1.5) prior on θ. Each observation costs you c. What is the optimal fixed sample size? You may start using computers at any stage in the solution of this problem.

Problem 14.3 You are the Mayor of Solvantville and you are interested in estimating the difference in the concentration of a certain contaminant in the water supply of homes in two different sections of town, each with its own well. If you found that there is a difference you would further investigate whether there may be contamination due to industrial waste. How big a sample of homes do you need for your purposes? Specify a terminal loss function, a cost of observation, a likelihood, and a prior. Keep it simple, but justify your assumptions and point out limitations.

Problem 14.4 In the context of Section 14.3.2 determine the optimal n by minimizing r(π, n).

Problem 14.5 Suppose x has a normal distribution with mean θ and variance σ². Let f (.) denote its density function.

1. Prove that , where z = (u – θ)/σ, and φ and Φ denote, respectively, the density and the cumulative distribution function of the standard normal distribution.

2. Define ζ (y) = φ(y) – y(1 – (y)). Prove that ζ (–y) = y + ζ (y).

3. Let and be, respectively, the right and left hand side linear loss integrals. Let z = (u – θ)/σ. Prove that

   1. A(u) = σζ (z).

   2. B(u) = σζ (–z).

Problem 14.6 In the context of the example of Section 14.3.3:

1. Derive the function g in equation (14.35) and prove that its first- and second-order derivatives with respect to r are as given in (14.36).

2. Prove that when z₀ > 0, a local maximum may or may not exist (that is, in the latter case, the optimal sample size is zero).

Problem 14.7 Can you find the optimal sample size in Example 14.3.1 when σ is not known? You can use a conjugate prior and standard results such as those of Sec. 3.3 in Gelman et al. (1995).