PART III: PROBLEMS

Section 8.1

8.1.1 Let = {B(N, θ);0 < θ < 1} be the family of binomial distributions.

(i) Show that the family of beta prior distributions = {β (p, q); 0 < p, q < ∞} is conjugate to .

(ii) What is the posterior distribution of θ given a sample of n i.i.d. random variables, having a distribution in ?

(iii) What is the predicted distribution of Xn + 1, given (X1, …, Xn)?

8.1.2 Let X1, …, Xn be i.i.d. random variables having a Pareto distribution, with p.d.f.

0 < ν < ∞ (A is a specified positive constant).

(i) Show that the geometric mean, , is a minimal sufficient statistic.

(ii) Suppose that ν has a prior G(λ, p) distribution. What is the posterior distribution of ν given X?

(iii) What are the posterior expectation and posterior variance of ν given X?

8.1.3 Let X be a p–dimensional vector having a multinormal distribution N(μ, ). Suppose that is known and that μ has a prior normal distribution N(μ0, V). What is the posterior distribution of μ given X?

8.1.4 Apply the results of Problem 3 to determine the posterior distribution of β in the normal multiple regression model of full rank, when σ2 is known. More specifically, let

8.1.5 Let X1, …, Xn be i.i.d. random variables having a Poisson distribution, P(λ), 0 < λ < ∞. Compute the posterior probability P{λ ≥ n | Xn} corresponding to the Jeffreys prior.

8.1.6 Suppose that X1, …, Xn are i.i.d. random variables having a N(0, σ2) distribution, 0 < σ2 < ∞.

(i) Show that if then the posterior distribution of 1/2 σ2 given S = is also a gamma distribution.

(ii) What is E{σ2 | S} and V{σ2 | S} according to the above Bayesian assumptions.

8.1.7 Let X1, …, Xn be i.i.d. random variables having a N(μ, σ2) distribution; −∞ < μ < ∞, 0 < σ < ∞. A normal–inverted gamma prior distribution for μ, σ2 assumes that the conditional prior distribution of μ, given σ2, is N(μ0, λ σ2) and that the prior distribution of 1/2σ2 is a . Derive the posterior joint distribution of (μ, σ2) given (, S2), where and S2 are the sample mean and variance, respectively.

8.1.8 Consider again Problem 7 assuming that μ and σ2 are priorly independent, with μ ∼ N(μ0, D2) and . What are the posterior expectations and variances of μ and of σ2, given (, S2)?

8.1.9 Let X ∼ B(n, θ), 0 < θ < 1. Suppose that θ has a prior beta distribution . Suppose that the loss function associated with estimating θ by is L(θ, ). Find the risk function and the posterior risk when L(, θ) is

(i) L(, θ) = ( − θ)2;

(ii) L(, θ) = ( − θ)2/θ (1 − θ);

(iii) L(, θ) = | − θ|.

8.1.10 Consider a decision problem in which θ can assume the values in the set {θ0, θ1}. If i.i.d. random variables X1, …, Xn are observed, their joint p.d.f. is f(xn;θ) where θ is either θ0 or θ1. The prior probability of {θ = θ0} is η. A statistician takes actions a0 or a1. The loss function associated with this decision problem is given by

8.1.11 The time till failure of an electronic equipment, T, has an exponential distribution, i.e., ; 0 < τ < ∞. The mean–time till failure, τ, has an inverted gamma prior distribution, 1/τ ∼ G(Λ, ν). Given n observations on i.i.d. failure times T1, …, Tn, the action is an estimator . The loss function is . Find the posterior risk of . Which estimator will minimize the posterior risk?

Section 8.2

8.2.1 Let X be a random variable having a Poisson distribution, P(λ). Consider the problem of testing the two simple hypotheses H0: λ = λ0 against H1: λ = λ1; 0 < λ0 < λ1 < ∞.

(i) What is the form of the Bayes test π (X), for a prior probability π of H0 and costs c1 and c2 for errors of types I and II.

(ii) Show that R0(π) = c1(1 − P([ξ (π)]; λ0)), where P(j; λ) is the c.d.f. of P(λ), R1(π) = c2P([ξ (π)]; λ1),

where [x] is the largest integer not exceeding x.

(iii) Compute (R0(π), R1(π)) for the case of c1 = 1, c2 = 3; λ1/λ0 = 2, λ1–λ0 = 2, and graph the lower boundary of the risk set R.

8.2.2 Let X1, …, Xn be i.i.d. random variables having an exponential distribution G(λ, 1), 0 < λ < ∞. Consider the two composite hypotheses H0: λ ≤ λ0 against H1: λ > λ0. The prior distribution of λ is . The loss functions associated with accepting Hi (i = 0, 1) are

and

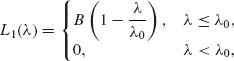
0 < B < ∞.

8.2.3 Let X1, …, Xn be i.i.d. random variables having a binomial distribution B(1, θ). Consider the two composite hypotheses H0: θ ≤ 1/2 against H1: θ > 1/2. The prior distribution of θ is β (p, q). Compute the Bayes Factor in favor of H1 for the cases of n = 20, T = 15 and

8.2.4 Let X1, …, Xn be i.i.d. random variables having a N(μ, σ2) distribution. Let Y1, …, Ym be i.i.d. random variables having a N(η, ρ σ2) distribution, −∞ < μ, η < ∞, 0 < σ2, ρ < ∞, The X–sample is independent of the Y–sample. Consider the problem of testing the hypothesis H0: ρ ≤ 1, (μ, η, σ2) arbitrary against H1: ρ > 1, (μ, η, σ2) arbitrary. Determine the form of the Bayes test function for the formal prior p.d.f. h(μ, η, σ, ρ) and a loss function with c1 = c2 = 1.

8.2.5 Let X be a k–dimensional random vector having a multinomial distribution M(n;θ). We consider a Bayes test of against . Let θ have a prior symmetric Dirichlet distribution (8.2.27) with ν = 1 or 2 with equal hyper–prior probabilities.

(i) Compute the Bayes Factor in favor of H1 when k = 5, n = 50, X1 = 7, X2 = 12, X3 = 9, X4 = 15, and X5 = 7. [Hint: Approximate the values of Γ(ν k + n) by the Stirling approximation: , for large n.]

(ii) Would you reject H0 if c1 = c2 = 1?

8.2.6 Let X1, X2, … be a sequence of i.i.d. normal random variables, N(0, σ2). Consider the problem of testing H0: σ2 = 1 against H1: σ2 = 2 sequentially. Suppose that c1 = 1 and c2 = 5, and the cost of observation is c = 0.01.

8.2.7 Let X1, X2, … be a sequence of i.i.d binomial random variables, B(1, θ), 0 < θ < 1. According to H1: θ = 0.3. According to H1: θ = 0.7. Let π, 0 < π < 1, be the prior probability of H0. Suppose that the cost for erroneous decision is b = 10[$] (either type of error) and the cost of observation is c = 0.1[$]. Derive the Bayes risk functions ρi(π), i = 1, 2, 3 and the associated decision and stopping rules of the Bayes sequential procedure.

Section 8.3

8.3.1 Let X ∼ B(n, θ) be a binomial random variable. Determine a (1 – α)–level credibility interval for θ with respect to the Jeffreys prior h(θ) ∝ θ−1/2(1-θ)−1/2, for the case of n = 20, X = 17, and α = 0.05.

8.3.2 Consider the normal regression model (Problem 3, Section 2.9). Assume that σ2 is known and that (α, β) has a prior bivariate normal distribution .

(i) Derive the (1 − ) joint credibility region for (α, β).

(ii) Derive a (1 − ) credibility interval for α + β ξ0, when ξ0 is specified.

(iii) What is the (1 − ) simultaneous credibility interval for α + β ξ, for all ξ?

8.3.3 Consider Problem 4 of Section 8.2. Determine the (1–α) upper credibility limit for the variance ratio ρ.

8.3.4 Let X1, …, Xn be i.i.d. random variables having a N(μ, σ2) distribution and let Y1, …, Yn be i.i.d. random variables having a N(η, σ2) distribution. The Xs and the Ys are independent. Assume the formal prior for μ, η, and σ, i.e.,

8.3.5 Let X1, …, Xn be i.i.d. random variables having a G(λ, 1) distribution and let Y1, …, Ym be i.i.d. random variables having a G(η, 1) distribution. The Xs and Ys are independent. Assume that λ and η are priorly independent having prior distributions and , respectively. Determine a 1 – α) HPD–interval for ω = λ/η.

Section 8.4

8.4.1 Let X ∼ B(n, θ), 0 < θ < 1. Suppose that the prior distribution of θ is β (p, q), 0 < p, q < ∞.

(i) Derive the Bayes estimator of θ for the squared–error loss.

(ii) What is the posterior risk and the prior risk of the Bayes estimator of (i)?

(iii) Derive the Bayes estimator of θ for the quadratic loss L(, θ) = ( − θ)2/θ (1 − θ), and the Jeffreys prior .

(iv) What is the prior and the posterior risk of the estimator of (iii)?

8.4.2 Let X∼ P(λ), 0 < λ < ∞. Suppose that the prior distribution of λ is .

(i) Derive the Bayes estimator of λ for the loss function L(, λ) = a(–λ)+ + b(–λ)−, where (·)+ = max(·,) and (·)− = −min(·, 0); 0 < a, b < ∞.

(ii) Derive the Bayes estimator for the loss function L(, λ) = ( − λ)2/λ.

(iii) What is the limit of the Bayes estimators in (ii) when and .

8.4.3 Let X1, …, Xn, Y be i.i.d. random variables having a normal distribution N(μ, σ2); −∞ < μ < ∞, 0 < σ2 < ∞. Consider the Jeffreys prior with h(μ, σ2) dμ dσ2 ∝ dμ dσ2/σ2. Derive the γ–quantile of the predictive distribution of Y given (X1, …, Xn).

8.4.4 Let X ∼ P(λ), 0 < λ < ∞. Derive the Bayesian estimator of λ with respect to the loss function L(, λ) = ( – λ)2/λ, and a prior gamma distribution.

8.4.5 Let X1, …, Xn be i.i.d. random variables having a B(1, θ) distribution, 0 < θ < 1. Derive the Bayesian estimator of θ with respect to the loss function L(, θ) = ( − θ)2/θ (1 − θ), and a prior beta distribution.

8.4.6 In continuation of Problem 5, show that the posterior risk of = Σ X/n with respect to L(, θ) = ( − θ)2/θ (1 − θ) is 1/n for all Σ Xi. This implies that the best sequential sampling procedure for this Bayes procedure is a fixed sample procedure. If the cost of observation is c, determine the optimal sample size.

8.4.7 Consider the normal–gamma linear model where Y is four–dimensional and

(i) What is the predictive distribution of Y?

(ii) What is the Bayesian estimator ?

8.4.8 As an alternative to the hierarchical model of Gelman et al. (1995) described in Section 8.4.2, assume that n1, …, nk are large. Make the variance stabilizing transformation

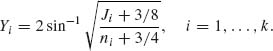
We consider now the normal model

where Y = (Y1, …, Yk)′, η = (η1, …, ηk)′ with ηi = 2sin−1, i = 1, …, k. Moreover, D is a diagonal matrix, D = . Assume a prior multinormal distribution for η.

8.4.9 Consider the normal random walk model, which is a special case of the dynamic linear model (8.4.6), given by

where θ0 ∼ N(η0, c0), {n} are i.i.d. N(0, σ2) and {ωn} are i.i.d. N(0, τ2). Show that , where cn is the posterior variance of θn, given (Y1, …, Yn). Find the formula of c*.

Section 8.5

8.5.1 The integral

can be computed analytically or numerically. Analytically, it can be computed as

8.5.2 Prove that if U1, U2 are two i.i.d. rectangular (0, 1) random variables then the Box Muller transformation (8.5.26) yields two i.i.d. N(0, 1) random variables.

8.5.3 Consider the integral I of Problem [1]. How would you approximate I by simulation? How would you run the simulations so that, with probability ≥ 0.95, the absolute error is not greater than 1% of I.

Section 8.6

8.6.1 Let (X1, θ1), …, (Xn, θn), … be a sequence of independent random vectors of which only the Xs are observable. Assume that the conditional distributions of Xi given θi are B(1, θi), i = 1, 2, …, and that θ1, θ2, … are i.i.d. having some prior distribution H(θ) on (0, 1).

(i) Construct an empirical–Bayes estimator of θ for the squared–error loss.

(ii) Construct an empirical–Bayes estimator of θ for the squared–error loss, if it is assumed that H(θ) belongs to the family = {β (p, q): 0 < p, q < ∞}.

8.6.2 Let (X1, 1), …, (Xn, n), … be a sequence of independent random vectors of which only the Xs are observable. It is assumed that the conditional distribution of Xi given i is NB(i, ν), ν known, i = 1, 2, …. Moreover, it is assumed that 1, 2, … are i.i.d. having a prior distribution H(θ) belonging to the family of beta distributions. Construct a sequence of empirical–Bayes estimators for the squared–error loss, and show that their posterior risks converges a.s. to the posterior risk of the true β (p, q).

8.6.3 Let (X1, λ1), …, (Xn, λn), … be a sequence of independent random vectors, where Xi | λi ∼ G(λi, 1), i = 1, 2, …, and λ1, λ2, … are i.i.d. having a prior distribution; τ and ν unknown. Construct a sequence of empirical–Bayes estimators of λi, for the squared–error loss.

PART IV: SOLUTIONS OF SELECTED PROBLEMS

8.1.6 (i) Since X ∼ N(0, σ2), . Thus, the density of S, given σ2, is

8.1.9

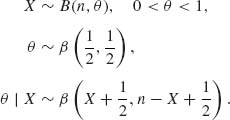
Accordingly,

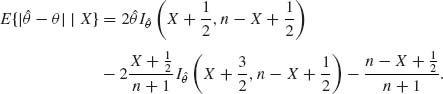
8.2.1 (i) The prior risks are R0 = c1π and R1 = c2(1 − π), where π is the prior probability of H0. These two risk lines intersect at π* = c2/(c1 + c2). We have R0(π*) = R1(π*). The posterior probability that H0 is true is

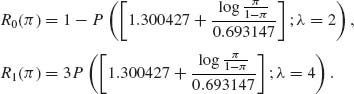
8.3.2 We have a simple linear regression model Yi = α + β xi + i, i = 1, …, n; where i are i.i.d. N(0, σ2). Assume that σ2is known. Let (X) = (1n, xn), where 1n is an n–dimensional vector of 1s, x′n = (x1, …, xn). The model is

(i) Let . The prior distribution of θ is N(θ0, ). Note that the covariance matrix of Y is V[Y] = σ2 I + (X)(X)′. Thus, the posterior distribution of θ, given Y, is N(η(Y), D), where

and

Accordingly

Thus, the (1–α) credibility region for θ is

(ii) Let and . The posterior distribution of θ′w0, given Y, is N(η(Y)′w0, w′0Dw0). Hence, a (1 – α) credibility interval for θ′w0, given Y, has the limits η(Y)′w0 ± z1 − /2(w′0 Dw0)1/2.

(iii) Simultaneous credibility interval for all ξ is by Sheffe’s S–intervals

8.4.1

The prior of θ is Beta (p, q), 0 < p, q < ∞.

(i) The posterior distribution of θ, given X, is Beta (p + X, q + n − X). Hence, the Bayes estimator of θ, for squared–error loss, is B = .

(ii) The posterior risk is V(θ | X) = . The prior risk is

(iii) The Bayes estimator is

8.4.3 The Jeffreys prior is . A version of the likelihood function, given the minimal sufficient satistic (, Q), where Q = , is

Thus, the posterior density under Jeffrey’s prior is

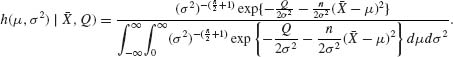
Now,

Furthermore,

Accordingly,

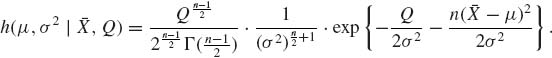
Thus, the predictive density of Y, given [, Q], is

or

Recall that the density of t[n − 1] is

Thus, the γ–quantile of the predictive distribution fH(y | , Q) is + .

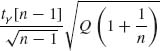8.5.3

where U ∼ β (X + 1, n- X + 1). By simulation, we generate M i.i.d. values of U1, …, UM, and estimate I by . For large , where D = B2(X +1, n − X + 1)V{e−U}. We have to find M large enough so that ≥ 0.95. According to the asymptotic normal distribution, we determine M so that

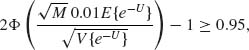
or

By the delta method, for large M,

Similarly,

Hence, M should be the smallest integer such that