Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 5
Tensors on Vector Spaces

5.1 Tensors

Let V be a vector space, and let r, s ≥ 1 be integers. Following Section B.5 and Section B.6, we denote by Mult(V*^r × V ^s, ℝ) the vector space of ℝ‐multilinear functions from V*^r × V ^s to ℝ, where addition and scalar multiplication are defined as follows: for all functions ?, ℬ, in Mult(V*^r × V ^s, ℝ) and all real numbers c,

and

for all covectors η ^r, … , η ^r in V* and all vectors v ₁, … , v _s in V. For brevity, let us denote

We refer to a function ? in as an ( r, s )‐tensor, an r‐contravariant‐s‐covariant tensor, or simply a tensor on V, and we define the rank of to be (r, s). When s = 0, ? is said to be an r‐contravariant tensor or just a contravariant tensor, and when r = 0, ? is said to be an s‐covariant tensor or simply a covariant tensor. In Section 1.2, we used the term covector to describe what we now call a 1‐covariant tensor. Note that the sum of tensors is defined only when they have the same rank. The zero element of , called the zero tensor and denoted by 0, is the tensor that sends all elements of V*^r × V ^s to the real number 0. A tensor in is said to be nonzero if it is not the zero tensor. Let us observe that

(5.1.1)

For completeness, we define

(5.1.2)

It is important not to confuse the above vector space operations with the multilinear property. The latter means that a tensor is linear in each of its arguments. That is, for all covectors η ¹, … , η ^r, ζ in V*, all vectors v ₁, … , v _s, w , W in V, and all real numbers c, we have

for i = 1,..., r, and

for j = 1,..., s.

Example 5.1.1

The classic example of a tensor is the determinant function det, which is an m‐covariant tensor on Mat_{m × 1}. Another obvious example is a bilinear function b on a vector space V, which is a 2‐covariant tensor on V. Here are two more examples of tensors. For given vectors V, W in V, the function ? : V ^*2 → ℝ defined by ?(η, ζ) = η(v)ζ(w) for all covector η, ζ in V* is a 2‐contravariant tensor on V*. Similarly, for given covectors η, ζ in V*, the function ℬ : V ² → ℝ defined by ℬ(v, w) = η(v)ζ(w) for all vector V, W in V is a 2‐covariant tensor on V.

Computations involving tensors rely in a crucial way on the identification V** = V, which is included as part of (5.1.1). We repeat here the remarks made at the close of Section 1.2: for a vector V in V and a covector η in V*, the element of V ^** corresponding to v is also denoted by v, so that, by definition,

(5.1.3)

Thus, ℬ in Example 5.1.1 can be expressed as ℬ(v, w) = v(n)w(ζ). Despite (5.1.3), we usually prefer the notation η(v) to v(η).

We now define a type of multiplication of tensors. Tensor product is the family of linear maps

defined for r, s, r′, s′ ≥ 0 by

(5.1.4)

for all tensors ? in and ℬ in , all covectors in V*, and all vectors in V. We refer to ? ⊗ ℬ as the tensor product of ? and ℬ. Unlike with addition, the product of tensors does not require ? and ℬ to have the same rank. Usually, ? ⊗ ℬ ≠ ℬ ⊗ ?, so the tensor product is generally not commutative.

The next result gives the basic algebraic properties of tensors.

In view of Theorem 5.1.2(d), we drop parentheses around tensor products and, for example, denote (? ⊗ ℬ) ⊗ ? and ? ⊗ (ℬ ⊗ ?) by ? ⊗ ℬ ⊗ ?, with corresponding notation for tensor products of more than three terms. By forming the tensor product of collections of vectors and covectors, we can construct tensors of arbitrary rank. To illustrate, from vectors w ₁, … , w _r in V and covectors ζ ¹, … , ζ ^s in V*, we obtain the tensor w ₁ ⊗ ⋯ ⊗ w _r ⊗ ζ ¹ ⊗ ⋯ ⊗ ζ ^s in . Then (5.1.4) gives

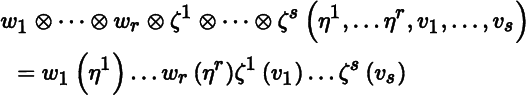
for all all covectors η ¹, … , η ^r in V* and all vectors v ₁, … , v _s in V.

Let V be a vector space, let ? be a tensor in , let ℋ = (h ₁, … , h _m) be a basis for V, and let Θ = (θ ₁, … , θ ^m) be its dual basis. The components of ? with respect to ℋ are defined by

for all 1 ≤ i ₁, … , i _r ≤ m and 1 ≤ j ₁, … , j _s ≤ m .

We see from Theorem 5.1.3 that a tensor is completely determined by its components with respect to a given basis. In fact, this is the classical way of defining a tensor. Choosing another basis generally yields different values for the components. The next result shows how to convert components when changing from one basis to another.

Theorem 5.1.5 shows that the product of tensors, each of which is expressed in the standard format given by (5.1.5), can in turn be expressed in that same format.

5.2 Pullback of Covariant Tensors

In this brief section, we generalize to tensors the definition of pullback by a linear map given in Section 1.3. Let V and W be vector spaces, and let A: V → W be a linear map. Pullback by A (for covariant tensors) is the family of linear maps

defined for s ≥ 1 by

(5.2.1)

for all tensors ℬ in and all vectors v ₁,…, v _s in V. We refer to A*(ℬ) as the pullback of ℬ by A . When s = 1, the earlier definition is recovered. As an example, let (V, g) be a scalar product space, and let A: V → V be a linear map. Then the tensor A*(g) in is given by A * (g)(v, w) = 〈A(v), A(w)〉for all vectors v, w in V.

Pullbacks of covariant tensors behave well with respect to basic algebraic structure.

5.3 Representation of Tensors

Let V be a vector space, let ℋ = (h ₁, … , h _m) be a basis for V, let (θ ¹, … , h ^m) be its dual basis, and let s ≥ 1 be an integer. Following Section B.5 and Section B.6, we denote by Mult (V ^s, V) the vector space of ℝ‐multilinear maps from V ^s to V. Let us define a map

called the representation map, by

(5.3.1)

for all maps ψ in Mult (V ^s, V), all covectors η in V*, and all vectors v ₁,…,v _s in V. When s = 1, we denote

It is instructive to specialize Theorem 5.3.1 to the case s = 1, which for us is the situation of most interest. We then have Mult (V, V) = Lin (V, V) and

defined by

(5.3.2)

for all maps B in Lin (V, V), all covectors η in V*, and all vectors V in V.

Theorem 5.3.2(c) shows that each tensor in has a representation as a matrix. Continuing with Example 5.1.6, the tensor δ in has the components with respect to ℋ. By Theorem 5.3.2(c),

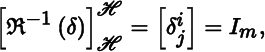
so, not surprisingly, ℜ⁻¹(δ) = id_V.

5.4 Contraction of Tensors

Contraction of tensors is closely related to the trace of matrices. Like dual vector spaces, it is another of those deceptively simple algebraic constructions that has far‐reaching applications.

Theorem 5.4.2 explains why in the literature “contraction” is sometimes called “trace”. The next result is a generalization of Theorem 5.4.1.

Proof

Existence.

Let ? be a tensor in , let ζ ¹, … , ζ ^k − 1, ζ ^k + 1, … , ζ ^r be covectors in V*, and let w ₁, … , w _l − 1, w _l + 1, … , w _s be vectors in V. We temporarily treat the preceding covectors and vectors as fixed and define a tensor in by the assignment

for all covectors ζ in V* and all vectors W in V. Using Theorem 5.4.1, we obtain the corresponding (1, 1)‐contraction Allowing ζ ¹, … , ζ ^k − 1, ζ ^k + 1, … , ζ ^r and w ₁, … , w _l − 1, w _l + 1, … , w _s to vary defines a tensor It follows from

and Theorem 5.4.1 that

Since ζ ¹, … , ζ ^k − 1, ζ ^k + 1, … , ζ ^r, w ₁, … , w _l − 1, w _l + 1, … , w _s were arbitrary, the result follows.

Uniqueness. This follows from the uniqueness property of described in Theorem 5.4.1.

We say that (k, l) is the rank of a (k, l)‐contraction. The composite of contractions (of various ranks) is called simply a contraction. We sometimes refer to the type of contractions defined here as ordinary, to distinguish them from a variant to be described in Section 6.5.