Chapter 1
Vector Spaces
1.1 Vector Spaces
The definition of a vector space over a field and that of a subspace of a vector space are given in Section B.6. Our focus in this book is exclusively on vector spaces over the real numbers (as opposed to the complex numbers or some other field).
Throughout, all vector spaces are over 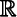 , the field of real numbers
, the field of real numbers
For brevity, we will drop the reference to ℝ whenever possible and write, for example, “linear” instead of “ℝ‐linear”.
Of particular importance is the vector space ℝ m , but many other examples of vector spaces will be encountered. It is easily shown that the intersection of any collection of subspaces of a vector space is itself a subspace. The zero vector of a vector space is denoted by 0, and the zero subspace of a vector space by {0}. The zero vector space, also denoted by {0}, is the vector space consisting only of the zero vector. We will generally avoid explicit consideration of the zero vector space. Most of the results on vector spaces either apply directly to the zero vector space or can be made applicable with a minor reworking of definitions and proofs. The details are usually left to the reader.
A linear combination of vectors in a vector space V is defined to be a finite sum of the form a 1 v 1 + … + a k v k , where a 1, …, a k are real numbers and v 1, …, v k are vectors in V. The possibility that some (or all) of a 1, …, a k equal zero is not excluded.
Let us pause here to comment on an aspect of notation. Following the usual convention in differential geometry, we index the scalars and vectors in a linear combination with superscripts and subscripts, respectively. This opens the door to the Einstein summation convention, according to which, for example,
a
1
v
1 + … + a
k
v
k
and ![]() are abbreviated as
a
i
v
i
. The logic is that when an expression has a superscript and subscript in common, it is understood that the index is being summed over. Despite the potential advantages of this notation, especially when multiple indices involved, the Einstein summation convention will not be adopted here.
are abbreviated as
a
i
v
i
. The logic is that when an expression has a superscript and subscript in common, it is understood that the index is being summed over. Despite the potential advantages of this notation, especially when multiple indices involved, the Einstein summation convention will not be adopted here.
Let S be a (nonempty and not necessarily finite) subset of V. The span of S is denoted by span (S) and defined to be the set of linear combinations of vectors in S:
For a vector v in V, let us denote
For example, in ![]() 2, we have
2, we have
and
It is easily shown that span (S) is a subspace of V. In fact, span (S) is the smallest subspace of V containing S, in the sense that any subspace of V containing S also contains span (S). When span (S) = V, it is said that S spans V or that the vectors in S span V , and that each vector in V is in the span of S .
We say that S is linearly independent or that the vectors in S are linearly independent if the only linear combination of distinct vectors in S that equals the zero vector is the one with all coefficients equal to 0. That is, if v
1,…, v
k
are distinct vectors in S and a
1, …, a
k
are real numbers such that a
1
v
1 + … + a
k
v
k
= 0, then a
1 = … = a = 0. Evidently, any subset of a linearly independent set is linearly independent. When S is not linearly independent, it is said to be linearly dependent. In particular, the zero vector in any vector space is linearly dependent. As further examples, the vectors (1, 0), (0, 1) in ![]() 2 are linearly independent, whereas (0, 0), (1, 0) and (1, 0), (2, 0) are linearly dependent.
2 are linearly independent, whereas (0, 0), (1, 0) and (1, 0), (2, 0) are linearly dependent.
The next result shows that when a linearly independent set does not span a vector space, it has a linearly independent extension.
A (not necessarily finite) subset ℋ of a vector space V is said to be an unordered basis for V if it spans V and is linearly independent.
We say that a vector space is finite‐dimensional if it has a finite unordered basis. Finite‐dimensional vector spaces have an associated invariant that, as we will see, largely characterizes them.
For completeness, we assign the zero vector space the dimension 0:
Throughout the remainder of Part I, unless stated otherwise, all vector spaces are finite‐dimensional
Let V be a vector space, and let {h 1, … , h m } be an unordered basis for V. The m‐tuple (h 1, … , h m ) is said to be an ordered basis for V, as is any m‐tuple derived from (h 1, … , h m ) by permuting h 1, … , h m . For example, (h 1, h 2, … , h m ) and (h 2, h 1, … , h m ) are distinct ordered bases for V.
Throughout the remainder of Part I, unless stated otherwise, all bases are ordered
Accordingly, we now refer to (e
1, … , e
m
) as the standard basis for ![]() m
. Let V and W be vector spaces. A map A: V → W is said to be linear if
m
. Let V and W be vector spaces. A map A: V → W is said to be linear if
for all vectors v, w in V and all real numbers c. Thus, a linear map respects vector space structure. Suppose A is in fact a linear map. Given a basis ℋ = (h 1, … , h m ) for V, let us denote
We say that A is a linear isomorphism, and that V and W are isomorphic, if A is bijective. To illustrate, let x be an indeterminate, and let
be the set of real polynomials of degree at most m. From the properties of polynomials, it is easily shown that ![]() is a vector space of dimension m + 1, and that the map
A : ℙ
m + 1 → ℙ
m
given by
A(a
0, … , a
m
) = a
0 + a
1
x + … + a
m
x
m
for all vectors (a
0, … , a
m
) in R
m + 1 is a linear isomorphism. Following Section B.5, we denote the existence of an isomorphism by
R
m + 1 ≈ P
m
.
is a vector space of dimension m + 1, and that the map
A : ℙ
m + 1 → ℙ
m
given by
A(a
0, … , a
m
) = a
0 + a
1
x + … + a
m
x
m
for all vectors (a
0, … , a
m
) in R
m + 1 is a linear isomorphism. Following Section B.5, we denote the existence of an isomorphism by
R
m + 1 ≈ P
m
.
Since a linear isomorphism is a bijective map, it has an inverse map. The next result shows that the inverse of a linear isomorphism is automatically a linear isomorphism.
A linear map is completely determined by its values on a basis, as we now show.
From the point of view of linear structure, isomorphic vector spaces are indistinguishable. In fact, it is easily shown using Theorem 1.1.10 that all m‐dimensional vector space are isomorphic. More than that, they are all isomorphic to ![]() m
. The isomorphism constructed with the help of Theorem 1.1.10 depends on the choice of bases for the vector spaces. However, we will see an instance in Section 1.2 where an isomorphism can be defined without having to resort to such an arbitrary choice.
m
. The isomorphism constructed with the help of Theorem 1.1.10 depends on the choice of bases for the vector spaces. However, we will see an instance in Section 1.2 where an isomorphism can be defined without having to resort to such an arbitrary choice.
Let V and W be vector spaces, and let A : V → W be a linear map. The kernel of A is defined by
and the image of A by
It is easily shown that ker (A) is a subspace of V, and im (A) is a subspace of W. The nullity of A is defined by
and the rank of A by
The nullity and rank of a linear map satisfy an important identity.
As an example of the rank‐nullity identity, consider the linear map A : ℝ3 → ℝ2 given by A(x, y, z) = (x + y, 0). Then
and
In geometric terms, ker (A) is a plane in ![]() 3 and im (A) is a line in
3 and im (A) is a line in ![]() 2. Thus, null (A) = 2 and rank (A) = 1, which agrees with Theorem 1.1.11.
2. Thus, null (A) = 2 and rank (A) = 1, which agrees with Theorem 1.1.11.
In the notation of Theorem 1.1.11, we observe from (1.1.2) that rank (A) ≤ dim (V). Thus, a linear map at best “preserves” dimension, but never increases it.
We pause here to comment on the way proofs are presented when there is an equation or other type of display that stretches over several lines of text. The necessary justification for logical steps in such displays, whether it be equation numbers, theorem numbers, example numbers, and so on, are often provided in brackets at the end of corresponding lines. In order to economize on space, “[Theorem x.y.z]” and “[Example x.y.z]” are abbreviated to “[Th x.y.z]” and “[Ex x.y.z]”. The proof of the next result illustrates these conventions.
Let V be a vector space, and let U 1,…,U k be subspaces. The sum of U 1 ,…,U k is denoted by U 1 + … + U k and defined by
For example, ![]() (1, 0) +
(1, 0) + ![]() (0, 1) =
(0, 1) = ![]() 2. It is easily shown that
2. It is easily shown that
from which it follows that U 1 + … + U k is the smallest subspace of V containing each of U 1,…, U k , in the sense that any subspace containing each of U 1,…, U k also contains U 1 + … + U k . We observe that
which shows that adding the zero vector spaces does not change a sum. For vectors v 1,…,v k in V, we have the following connection between spans and sums:
Let V be a vector space, and let U 1,…,U k be subspaces of V. We say that the subspace U 1 + … + U k of V is a direct sum, and write
if each vector V in U 1 + … + U k can be expressed uniquely (up to order of terms) in the form v = u 1 + … + u k for some vectors u i in U i for i = 1, … , k. As a matter of notation, writing V = U 1 ⊕ … ⊕ U k is shorthand for
For example, ℝ2 = ℝ(1, 0) ⊕ ℝ(0, 1).
Let V 1, … , V k be vector spaces. Following Section B.5, we make V 1 × … × V k into a vector space, called the product of V 1 ,…, V k , as follows: for all vectors (v 1, … , v k), (w 1, … , w k ) in V 1 × … × V k and all real numbers c, let
and
When V 1 = … = V k = V, we denote
We close this section with two definitions that have obvious geometric content. Let V be a vector space. A subset S of V is said to be star‐shaped if there is a vector v0 in S such that for all vectors v in S and all real numbers 0 ≤ t ≤ 1, the vector
tv + (1 − t)v
0
is in S. In that case, we say that S is star‐shaped about v
0
. Since
tv + (1 − t)v
0 = v
0 + t(v − v
0), we can think of {tv + (1 − t)v
0 : 0 ≤ t ≤ 1} as the “line segment” joining v
0 to V. A subset C of V is said to be cone‐shaped if for all vectors v, v
1,v
2 in C and all real numbers c > 0, the vectors cv and v
1 + v
2 are in C. It is easily shown that if C is cone‐shaped, then it is star‐shaped about any vector it contains. For example, the closed cell {(x, y) : x, y ∈ [−1, 1]} in ![]() 2 is star‐shaped about (0, 0), but not cone‐shaped; whereas the half‐plane {(x, y) ∈ ℝ2 : x > 0} in
2 is star‐shaped about (0, 0), but not cone‐shaped; whereas the half‐plane {(x, y) ∈ ℝ2 : x > 0} in ![]() 2 is cone‐shaped, hence star‐shaped about (0, 0).
2 is cone‐shaped, hence star‐shaped about (0, 0).
1.2 Dual Spaces
In this section, we define the dual (vector) space of a vector space. From this humble beginning, the theory of differential forms will eventually emerge (see Section 15.8).
Let V be a vector space. Following Section B.5 and Section B.6, we denote by Lin (V, ![]() ) the vector space of linear maps from V to
) the vector space of linear maps from V to ![]() . By definition, for all maps η, ζ in Lin (V,
. By definition, for all maps η, ζ in Lin (V, ![]() ) and all real numbers c,
) and all real numbers c,
and
for all vectors v in V. For brevity, we henceforth denote
We say that V* is the dual (vector) space of V and refer to each map in V* as a covector. As an example, the map
η : ℝ2 → ℝ given by
η(x, y) = x + y
is in (![]() 2)*. Let us denote
2)*. Let us denote
and say that V** is the double dual of V.
It is clear that ι is a linear map. Let (h 1,…, h m ) be a basis for V, and let (θ 1, … , θ m ) be its dual basis. If V is a vector in V such that ι (v) = 0, then η (v) = 0 for all covectors η in V*. In particular, θ i (v) = 0 for i = 1,…, m. It follows from Theorem 1.2.1 (d) that v = 0, hence ker (ι) = {0}. By Theorem 1.1.12, ι is injective. Using Theorem 1.2.1(c) twice yields
The result now follows Theorem 1.1.14.
In view of Theorem 1.2.2, and especially because ι was defined without choosing specific bases for V and V*, we adopt the following convention:
Throughout, we identify V** with V, and write V** = V
Let V be a vector in V, and let η be a covector in V*. Having made the identification V** = V, we henceforth denote
Thus, (1.2.1) and (1.2.2) both become
In particular, we have
for i, j = 1,…, m.
1.3 Pullback of Covectors
In Section 1.2, we introduced the dual space of a vector space. Continuing with that theme, we now associate with a given linear map a corresponding linear map between their dual spaces.
Let V and W be vector spaces, and let A: V → W be a linear map. Pullback by A is the linear map
defined by
for all covectors η in W*; that is,
for all vectors v in V. We refer to A*(η) as the pullback of η by A . Note that the pullback “reverses the order” of vector spaces. Let us denote
and observe that with the identifications V** = V and W** = W, we have
As an example, consider the map A: ![]() 3 →
3 → ![]() 2 defined by
A(x, y, z) = (x + z, y + z) for all vectors (x, y, z) in
2 defined by
A(x, y, z) = (x + z, y + z) for all vectors (x, y, z) in ![]() 3, and let η be the covector in (
3, and let η be the covector in (![]() 2)* given by η (x, y) = x + y. Then
2)* given by η (x, y) = x + y. Then
Pullbacks behave well with respect to basic algebraic structure.
Theorem 1.3.1
Lei U, V, and W be vector spaces, and let A, B : U → V and C : V → W be linear maps. Then:
- (A + B)* = A* + B*.
- (C o B)* = B* o C*.
- A ** = A.
- If A is a linear isomorphism, then (A –1)* = (A*)–1.
- A is a linear isomorphism if and only if A* is a linear isomorphism.
(a), (b): Straightforward.
(c): For a vector V in V and a covector η in W*, we have
Since v and η were arbitrary, A ** = A.
(d): By part (b),
from which the result follows.
(e) (⇒): Since A is a linear isomorphism, we have from Theorem 1.1.13(b) that dim (V) = dim (W), and then from Theorem 1.2.1(c) that dim (V*) = dim (W*). If η is a covector in W* such that A*(η) = 0, then (1.3.1) gives η (A(v)) = 0 for all vectors V in V. Since A is surjective, η (w) = 0 for all vectors W in W, hence η = 0. Thus, ker (A*) = {0}. The result now follows from Theorem 1.1.12 and Theorem 1.1.14.
(e) (⇐): Since A*: W* → V* is a linear isomorphism, we have from (e) (⇒) that so is A**: V** → W**. Then part (c) and the identifications V = V** and W = W** give the result.
1.4 Annihilators
Let V be a vector space, and let U be a subspace of V. The annihilator of U in V is denoted by U 0 and defined by
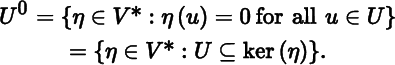
It is easily shown that U 0 is a subspace of V*. Let us denote
and observe that with the identification V** = V, U 00 is a subspace of V.
Theorem 1.4.1
If V is a vector space and U is a subspace of V, then
If U is the zero subspace, the result is trivial, so assume otherwise. Let (h 1, … , h k ) be a basis for U. Using Theorem 1.1.7(c), we extend (h 1, … , h k ) to a basis (h 1, … , h k , h k + 1, … , h m ) for V. Let (θ 1, … , θ k , θ k + 1, … , θ m ) be its dual basis, so that (θ k + 1, … , θ m ) is the dual basis of (h k + 1, … , h m ). It follows from θ i (h 1) = … = θ i (h k ) = 0 for i = k + 1,…, m that θ k + 1, … , θ m are covectors in U 0. We claim that (θ k + 1, … , θ m ) is a basis for U 0. For a covector η in U 0, we have from Theorem 1.2.1(e) that
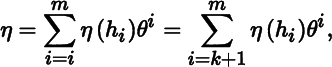
hence θ k + 1, … , θ m span U 0. Since (θ 1, … , θ m ) is a basis for V*, it follows that θ k + 1, … , θ m are linearly independent. This proves the claim. By Theorem 1.1.5,
Theorem 1.4.2
If V is a vector space and U is a subspace of V, then
If U is in U, then u(η) = η(u) = 0 for all covectors η in U 0, hence U is in U 00. Thus, U ⊆ U 00. We have
so dim (U) = dim (U 00). The result now follows from Theorem 1.1.7(b).
Theorem 1.4.3
Let V and W be vector spaces, and let A : V → W be a linear map. Then:
- rank (A*) = rank (A).
- If dim (V) = dim (W), then null (A*) = null (A).
- ker (A*) = im (A)0.
- im (A*) = ker (A)0.
(c): We have

(d): It follows from Theorem 1.3.1(c) and part (c) that
and then from Theorem 1.4.2 that
(a): We have
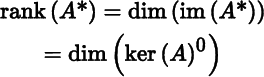
(b): We have
The result now follows from part (a).
