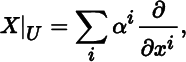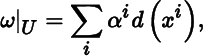In this chapter, we provide a generalization of vector fields to smooth manifolds and define a range of other types of “fields”.

15.1 Vector Fields

Vector fields arise in a variety of contexts. In this section, we discuss vector fields on smooth manifolds, curves, parametrized surfaces, and submanifolds.

Smooth manifolds . Let M be a smooth manifold. A vector field on M is a map X that assigns to each point p in M a vector X _p in T _p (M). As was the case for vector fields on regular surfaces, we sometimes use “∣ _p ” notation as an alternative to “subscript p ” notation, especially when other subscripts are involved. According to (14.3.1), X _p satisfies the product rule

(15.1.1)

for all functions f, g in C ^∞(M).

Let f be a function in C ^∞(M), and let

be the function defined by

(15.1.2)

for all p in M . It follows from (15.1.1) that

(15.1.3)

We say that X is smooth (on M ) if X(f) is in C ^∞(M) for all functions f in C ^∞(M). The set of smooth vector fields on M is denoted by . We make into both a vector space over ℝ and a module over C ^∞(M) by defining operations as follows: for all vector fields X, Y in , all functions f in C ^∞(M), and all real numbers c , let

and

for all p in M .

Looking back at the definition of a smooth vector field X : U → ℝ ^m between Euclidean spaces as presented in Section 10.3, we observe that for each point p in U , the vector X _p was taken to be in ℝ ^m With hindsight, it appears that we were implicitly identifying the tangent space T _p (ℝ ^m ) with ℝ ^m _.

The next result guarantees that for a given vector in a tangent space, there is always a smooth vector field with that vector as a value. Its proof (not given) relies on bump functions.

Let M be a smooth m ‐manifold, and let U be an open set in M . Viewing U as an m ‐manifold, let X ₁, …, X _m be vector fields in . The m ‐tuple is said to be a frame on U if is a basis for T _p (U) for all p in U . We will see later in this section that for each point p in M , there is always a neighborhood of p on which there is a frame. However, there may not be a frame on all of M .

Curves. Let M be a smooth manifold, and let λ : (a, b) → M be a smooth curve. A vector field on λ is a map J that assigns to each point t in (a, b) a vector J(t) in T _λ(t)(M). We observe that there is no requirement that λ be injective, so the image of λ might self‐intersect. As a consequence, there could be two (or more) distinct vectors assigned to a given point in λ((a, b)). This represents a distinct difference between a vector field on a curve and a vector field on a smooth manifold.

Let f be a function in C ^∞(M), and consider the function

defined by

(15.1.4)

for all t in (a, b). We say that J is smooth (on λ ) if J(f) is in C ^∞((a, b)) for all functions f in C ^∞(M). The set of smooth vector fields on λ is denoted by . Recall from Section 14.7 that the velocity of λ at t is (dλ/dt)(t). The velocity of λ is the vector field on λ defined by the assignment t ↦ (dλ/dt)(t) for all t in (a, b). We say that λ is regular if its velocity is nowhere‐vanishing; that is, (dλ/dt)(t) is not the zero vector in T _λ(t)(M) for any t in (a, b).

Depending on λ , not every vector field J in arises as the composition of λ with some vector field in . For example, suppose the image of λ self‐intersects at the points t ₁, t ₂ in (a, b) and that J(t ₁) ≠ J(t ₂). Since every vector field in assigns to each point p in M a distinct vector, there is no vector field X in such that J = X ∘ λ .

Let J ₁, …, J _m be vector fields in . The m ‐tuple is said to be a frame on λ if is a basis for T _λ(t)(M) for all t in (a, b).

Parametrized surfaces. Let M be a smooth manifold, and let σ(r, s) : (a, b) × (−ε, ε) → M be a parametrized surface. A vector field on σ is a map V that assigns to each point (r, s) in (a, b) × (−ε, ε) a vector V(r, s) in T _{σ(r, s)}(M). Once again, there is no requirement that σ be injective. Let f be a function in C ^∞(M), and consider the function

defined by

(15.1.5)

for all (r, s) in (a, b) × (−ε, ε). We say that V is smooth (on σ ) if V(f) is in C ^∞((a, b) × (−ε, ε)) for all functions f in C ^∞(M). The set of smooth vector Fields on σ is denoted by .

Recalling the notation in (14.9.1), we define a vector field ∂σ/∂r on σ by the assignment (r, s) ↦ (∂σ/∂r)(r, s), and likewise for ∂σ/∂s .

Submanifolds. Let be a smooth manifold, and let M be a submanifold. A vector field along M is a map V that assigns to each point p in M a vector V _p in . We note that V _p is required to be in but not necessarily in T _p (M). This explains the change in terminology to “along M _” from “on M _”.

Let f be a function in , and consider the function

defined by

for all p in M . We say that V is smooth (along M ) if V(f) is in C ^∞(M) for all functions f in . The set of smooth vector fields along M is denoted by . In particular, for each vector field X in , the restriction X| _M is in . With the usual definitions of addition and scalar multiplication, is a vector space over ℝ and a module over C ^∞(M). Furthermore, after making the appropriate identifications, is a C ^∞(M)‐submodule of . According to (14.8.1), for each point p in M, T _p (M) is a subspace of . We say that a vector field V in is nowhere‐tangent to M if V _p is not in T _p (M) for all p in M , or equivalently, if V _p is in for all p in M .

Let M be a smooth m ‐manifold, and let U be an open set in M . Recall from Theorem 14.8.4 that U is an open m ‐submanifold of M . Suppose U is the coordinate domain of a chart (U, (x ⁱ )) on M . The ith coordinate vector field of (U, (x ⁱ )) is the vector field

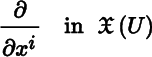
defined by the assignment

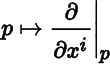
for all p in U for i = 1, …, m , where we denote

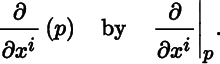
Then (∂/∂x ¹, …, ∂/∂x ^m ) is a frame on U , called the coordinate frame corresponding to (U, (x ⁱ )).

Let X be a (not necessarily smooth) vector field on M . Then X| _U can be expressed as

(15.1.6)

where the α ⁱ are uniquely determined functions on U , called the components of X with respect to (U, (x ⁱ )). For brevity, we denote

The right‐hand side of (15.1.6) is said to express X in local coordinates with respect to (U, (x ⁱ )). We often give the local coordinate expression of a vector field without mentioning the underlying chart. This should not introduce any confusion because the notation for the coordinate frame is imbedded in the notation used in (15.1.6), and the specifics of the coordinate domain are usually of no immediate interest.

15.2 Representation of Vector Fields

Let M be a smooth manifold. A linear map

is said to be a derivation [on C ^∞( M )] if it satisfies the following product rule:

(15.2.1)

for all functions f, g in C ^∞(M); that is,

for all p in M . The set of derivations on C ^∞(M) is denoted by Der(M). The zero derivation in Der(M), denoted by 0, is the derivation that sends all functions in C ^∞(M) to the zero function in C ^∞(M). We make Der (M) into both a vector space over ℝ and a module over C ^∞(M) by defining operations as follows: for all derivations in Der (M), all functions f, g in C ^∞(M), and all real numbers c , let

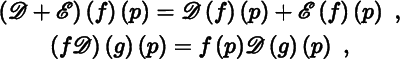
and

for all p in M .

We see from (15.1.3) that a vector field on M can be thought of as derivation on C ^∞(M). Pursuing this line of reasoning, let us consider the map

defined by

for all vector fields X in and all functions f in C ^∞(M); that is,

for all p in M , where the right‐hand side of the above identity is given by (15.1.2).

From now on, we often (but not always) identify with Der(M). However, we will continue to use the previous terminology and notation, and say, for example, that “ X is a vector field in ” rather than “ X is a derivation in Der(M)” It will usually be clear from the context whether the identification is being made, but sometimes, for emphasis, we make it explicit.

15.3 Lie Bracket

Let M be a smooth manifold, and let X and Y be vector fields in . The Lie bracket of X and Y is the map

defined by

(15.3.1)

for all functions f in C ^∞(M). Observe that this definition employs the representation of vector fields given by Theorem 15.2.1. Reverting for the moment to the vector field formulation, we have from (15.1.2) that

so that

for all p in M .

Lie bracket is the map

defined by the assignment

for all vector fields X, Y in .

It was observed in Section 15.1 that is a module over C ^∞(M). It follows from Theorem 15.3.2 that is also a Lie algebra over ℝ.

15.4 Covector Fields

Let M be smooth m ‐manifold. A covector field on M is a map ω that assigns to each point p in M a covector ω _p in . We say that ω vanishes at p if ω _p  = 0, is nonvanishing at p if ω _p  ≠ 0, and is nowhere‐vanishing (on M ) if it is nonvanishing at every p in M .

Let X be a vector field in X(M), and let

be the function defined by

(15.4.1)

for all p in M . We say that ω is smooth (on M ) if the function ω(X) is in C ^∞(M) for all vector fields X in . The set of smooth covector fields on M is denoted by . We make into both a vector space over ℝ and a module over C ^∞(M) by defining operations as follows: for all covector fields ω, ξ in , all functions f in C ^∞(M), and all real numbers c , let

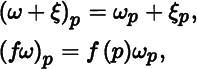
and

for all p in M . With the identification , we have from (5.1.3) that

for all p in M , which we express as

(15.4.2)

Let U be an open set in M . Viewing U as a smooth m ‐manifold, let ω ¹, …, ω ^m be covector fields in . The m ‐tuple ϒ = (ω ¹, …, ω ^m ) is said to be a dual frame on U if ϒ(p) = (ω ¹| _p , …, ω ^m | _p ) is a basis for for all p in U . Given a frame (X ₁, …, X _m ) on U , there is a uniquely determined dual frame (ω ¹, …, ω ^m ) on U defined as follows: (ω ¹| _p , …, ω ^m | _p ) is the dual basis corresponding to (X ₁| _p , …, X _m | _p ) for all p in U . Conversely, given a dual frame on U , there is a uniquely determined frame on U defined in the obvious way.

Suppose U is the coordinate domain of a chart (U, (x ⁱ )) on M . The ith coordinate covector field of (U, (x ⁱ )) is the covector field

defined by the assignment

for all p in U for i = 1, …, m . Then (d(x ¹), …, d(x ^m )) is a dual frame on U , called the dual coordinate frame corresponding to (U, (x ⁱ )).

Let ω be a (not necessarily smooth) covector field on M . Then ω| _U can be expressed as

(15.4.3)

where the α ⁱ are uniquely determined functions on U , called the components of ω with respect to (U, (x ⁱ )). For brevity, we denote

The right‐hand side of (15.4.3) is said to express ω in local coordinates with respect to (U, (x ⁱ )).

The next three results are the covector field counterparts to Theorem 15.1.2, Theorem 15.1.7, and Theorem 15.1.8.

Let M be a smooth manifold, and define a map

called the exterior derivative, by

(15.4.4)

for all functions f in C ^∞(M), all points p in M , and all vectors v in T _p (M), where the second equality follows from Theorem 14.5.5. Part (a) of the next result shows that this definition makes sense.

15.5 Representation of Covector Fields

Following Section B.5, we denote by

the C ^∞(M)‐module of C ^∞(M)‐linear maps from to C ^∞(M). Let us define a map

called the characterization map, by

(15.5.1)

for all covector fields ω in and all vector fields X in , where the right‐hand side of (15.5.1) is given by (15.4.1). It follows from Theorem 15.5.1 that ℭ(ω) is a map in , C ^∞(M)), so the definition makes sense. At this point, ℭ(ω) amounts to little more than notational shorthand for viewing the covector field ω in from the perspective of (15.4.1): as a mechanism for turning vector fields into functions. The purpose of this formalism will become clear as we proceed.

We say that an ℝ‐linear map ℱ : is determined point‐wise if for all points p in M , we have whenever are vector fields in such that . Since is equivalent to , and is equivalent to is determined pointwise if and only if for every point p in M, ℱ(Y)(p) = 0 whenever Y is a vector field in such that Y _p  = 0.

Let ω be a covector field in , let p be a point in M , and let X be a vector field in such that X _p  = 0. It follows from (15.4.1) and (15.5.1) that ℭ(ω)(X)(p) = 0. Thus, ℭ(ω) is a map in that is determined pointwise. Remarkably, as the next result shows, all maps in , have this property.

It is useful to isolate an aspect of the proof of Theorem 15.5.3. Let ϒ be a map in . We showed that ℭ⁻¹(ϒ) is the covector field in defined by

(15.5.4)

for all points p in M and all vectors v in T _p (M), where X is any vector field in such that X _p  = v , the existence of which is guaranteed by Theorem 15.1.2.

Now that we have Theorem 15.5.3, we usually (but not always) view as the vector space over ℝ and module over C ^∞(M) consisting of all C ^∞(M)‐linear maps from to C ^∞(M). We will see a significant generalization of Theorem 15.5.3 in Section 15.7.

15.6 Tensor Fields

In this section, we generalize some of the material in Section 15.4.

Let M be a smooth m ‐manifold, and let r, s ≥ 0 be integers. An ( r ,  s )‐tensor field on M is a map that assigns to each point p in M an (r, s) tensor in . We also refer to as an r‐contravariant‐s‐covariant tensor field or simply a tensor field, and we define the rank of to be (r, s). When is said to be an r‐contravariant tensor field or just a contravariant tensor field; and when is said to be an s‐covariant tensor field or simply a covariant tensor field.

Let ω ¹, …, ω ^r be covector fields in , let X ₁, …, X _s be vector fields in , and consider the function

defined by

(15.6.1)

for all p in M . We say that is smooth (on M ) if the function is in C ^∞(M) for all covector fields ω ¹, …, ω ^r in and all vector fields X ₁, …, X _s in . The set of smooth (r, s)‐tensor fields on M is denoted by . In particular,

(15.6.2)

For completeness, we define

(15.6.3)

It is instructive to compare identities (15.6.2) and (15.6.3) to identities (5.1.1) and (5.1.2). From now on, we avoid the following trivial case.

Throughout, unless stated otherwise, ( r ,  s ) ≠ (0, 0).

Defining operations on in a manner analogous to that described for vector fields and covector fields, we make into both a vector space over ℝ and a module over C ^∞(M).

Many of the definitions presented for smooth manifolds are expressed in a pointwise fashion (not to be confused with “determined pointwise”) and ultimately rest on earlier definitions given in the context of vector spaces. For example, a tensor field on a smooth manifold is essentially a collection of tensors, one for each point in the smooth manifold. An important consequence of the pointwise approach is that earlier theorems presented for vectors spaces generalize immediately to smooth manifolds. We will say that the resulting smooth manifold theorem is the manifold version (abbreviated mv) of the earlier vector space theorem. Here is an example.

Let M be a smooth m ‐manifold, and let (U, (x ⁱ )) be a chart on M . Let 1 ≤ i ₁, …, i _r  ≤ m and 1 ≤ j ₁, …, j _s  ≤ m be integers, and consider the tensor field

defined by the assignment

for all p in U . Suppose is a (not necessarily smooth) (r, s)‐tensor field on M . Then can be expressed as

(15.6.4)

where the are uniquely determined functions on U , called the components of with respect to (U, (x ⁱ )). For brevity, we denote

The right‐hand side of (15.6.4) is said to express in local coordinates with respect to (U, (x ⁱ )).

15.7 Representation of Tensor Fields

In this section, we present generalizations of the definitions and results of Section 15.5.

Let M be a smooth manifold, and let r, s ≥ 0 be integers. Following Section B.5, we denote by the C ^∞(M)‐module of C ^∞(M)‐multilinear maps from to C ^∞(M). Let us define a map

called the characterization map, by

(15.7.1)

for all tensor fields in , all covector fields ω ¹, …, ω ^s in , and all vector fields X ₁, …, X _s in , where the right‐hand side of (15.7.1) is given by (15.6.1). It follows from a generalization of Theorem 15.5.1 that is C ^∞(M)‐multilinear. Thus, is in , so the definition makes sense.

We say that an ℝ‐linear map ℱ : is determined pointwise if for all points p in M ,

whenever are covector fields in such that for i = 1, …, r , and are vector fields in such that for j = 1, …, s .

Let ϒ be a map in . Analogous to (15.5.4), is the tensor field in defined by

(15.7.2)

for all points p in M , all covectors η ¹, …, η ^r in , and all vectors v ₁, …, v _s in T _p (M), where ω ¹, …, ω ^r are any covector fields in such that ω ⁱ | _p  = η ⁱ for i = 1, …, r , and X ₁, …, X _s are any vector fields in such that X _j | _p  = v _j for j = 1, …, s .

For the remainder of this section, we attempt to place the above technical material in a larger context.

Let be a tensor field in . For a given point p in is a tensor in , and for given covectors η ¹, …, η ^r in and vectors v ₁, …, v _s in T _p (M), is its value in ℝ. Making the identification given by the isomorphism in Theorem 15.7.2, can now viewed as a map in . For given covector fields ω ¹, …, ω ^r in and vector fields X ₁, …, X _s in , is a function in C ^∞(M), and for a given point p in is its value in ℝ. The innovation introduced by Theorem 15.7.2 is that we have gone from evaluating the tensor at covectors and vectors to evaluating the function at forms and vector fields. Now that we have Theorem 15.7.2 at our disposal, we often (but not always) view as the vector space over ℝ and module over C ^∞(M) consisting of all C ^∞(M)‐multilinear maps from to C ^∞(M). We will not be fastidious about whether “ ” is included in the notation, allowing the context to make the situation clear and thereby providing a welcome simplification of notation.

An advantage of our new approach to tensor fields is the mechanism it provides for deciding whether a given map

is (or at least can be identified with) a tensor field in . According to Theorem 15.7.2, this identification can be made as long as ℱ can be shown to be C ^∞(M)‐multilinear. In practice, deciding if ℱ is additive is usually straightforward. The challenge typically resides in determining whether functions in C ^∞(M) can be “factored out” of ℱ. That is, if for all covector fields ω ¹, …, ω ^r in , all vector fields X ₁, …, X _s in , and all functions f in C ^∞(M), we have

for i = 1, …, r , and

for j = 1, …, s . We will encounter several instances of such computations in subsequent chapters.

Let us close this section with a few remarks on “representations”. In Section 15.2, we showed that a vector field in is equivalent to a type of map from C ^∞(M) to C ^∞(M). In Section 15.5, it was demonstrated that a covector field in is equivalent to a type of map from to C ^∞(M). In this section, we showed (or at least asserted) that a tensor field in is equivalent to a type of map from χ * (M) ^r  × X(M) ^s to C ^∞(M). Loosely speaking, we have been involved in a campaign to represent “fields” as maps that produce “functions”.

15.8 Differential Forms

Let M be a smooth m ‐manifold, and let 0 ≤ s ≤ m be an integer. A differential s ‐form on M is a map ω that assigns to each point p in M an s ‐covector ω _p in Λ ^s (T _p (M)). In the literature, a differential s ‐form is usually referred to as an s ‐form or simply a form. Observe that 1‐forms and covector fields are the same thing. Let X ₁, …, X _s be vector fields in , and define a function

by

for all p in M . We say that ω is smooth (on M ) if the function ω(X ₁, …, X _s ) is in C ^∞(M) for all vector fields X ₁, …, X _s in . The set of smooth s ‐forms on M is denoted by Λ ^s (M). Clearly, Λ ^s (M) is an ℝ‐subspace and C ^∞(M)‐submodule of , and

(15.8.1)

For completeness, and to be consistent with (15.6.3), let us define

(15.8.2)

In view of Theorem 7.2.12(b), we set Λ ^s (M) = {0} for s > m .

Let ω and ξ be forms in Λ ^s (M) and , respectively. We define a form ω ∧ ξ in , called the wedge product of ω and ξ , by

for all p in M . In particular, for a function f in C ^∞(M) = Λ⁰(M), we have

(15.8.3)

Let (U, (x ⁱ )) be a chart on M , let 1 ≤ i ₁ < ⋯ < i _r  ≤ m be integers, and let

be the map defined by the assignment

for all p in U . Suppose ω is a form in Λ ^s (M). Then ω| _U can be expressed as

(15.8.4)

where the are uniquely determined functions in C ^∞(U), called the components of ω with respect to (U, (x ⁱ )). For brevity, we denote

The right‐hand side of (15.8.4) is said to express ω in local coordinates with respect to (U, (x ⁱ )).

15.9 Pushforward and Pullback of Functions

Let M be a smooth manifold, and let F : M → N be a diffeomorphism. Pushforward by F (for functions) is the map

defined by

(15.9.1)

for all functions f in C ^∞(M).

Let M and N be smooth manifolds, and let F : M → N be a smooth map (but not necessarily a diffeomorphism). Pullback by F (for functions) is the map

defined by

(15.9.2)

for all functions g in C ^∞(N).

15.10 Pushforward and Pullback of Vector Fields

Let M and N be smooth manifolds, let F : M → N be a smooth map, let X be a vector field in , and let p be a point in M . By definition, d _p (F)(X _p ) is a vector in T _F(p)(N). Without further assumptions, the assignment p ↦ d _p (F)(X _p ) does not necessarily produce a vector field in . For example, if F is not surjective, there is no way to assign a vector to any point outside the image of F . Furthermore, if F is not injective, then there are distinct points p ₁, p ₂ in M such that F(p ₁) = F(p ₂). When , there is no unambiguous way to assign a vector to F(p ₁). The way out of this dilemma is to assume, as we now do, that F is a diffeomorphism. In what follows, we use

Theorem 15.2.1 to identify vector fields in with derivations in Der(M). The pushforward of X by F is the vector field F _*(X) in defined by

(15.10.1)

This definition makes sense because we have the maps F ^• : C ^∞(N) → C ^∞(M), X : C ^∞(M) → C ^∞(M), and F _• : C ^∞(M) → C ^∞(N), hence

Pushforward by F (for vector fields) is the map

defined by the assignment

for all vector fields X in . Pullback by F (for vector fields) is the map

defined by

that is,

(15.10.2)

for all vector fields Y in . We call F ^*(Y) the pullback of Y by F and observe that it equals the pushforward of Y by F ⁻¹ .

The notation F _* and F ^* will be used only when F is a diffeomorphism.

The next result shows that the pushforward provides a response to the issue raised in the introduction.

15.11 Pullback of Covector Fields

Let M and N be smooth manifolds, let F : M → N be a smooth map, and let p be a point in M . The corresponding differential map is d _p (F) : T _p (M) → T _F(p)(N). According to (7.1.2), and , so we have from (7.3.1) that the pullback by d _p (F) for covectors is the map

defined by

(15.11.1)

for all covectors η in and all vectors v in T _p (M). Pullback by F (for covector fields) is the linear map

defined by

(15.11.2)

for all covector fields ω in , all points p in M , and all vectors v in T _p (M), where the second equality follows from setting η = ω _F(p) in (15.11.1). We refer to F ^*(ω) as the pullback of ω by F . An important observation is that unlike the situation with pullbacks of vector fields, pullbacks of covector fields do not require diffeomorphisms for their definition.

15.12 Pullback of Covariant Tensor Fields

Let M and N be smooth manifolds, let F : M → N be a smooth map, and let p be a point in M . The corresponding differential map is d _p (F) : T _p (M) → T _F(p)(N). According to (5.2.1), the pullback by d _p (F) for covariant tensors is the family of linear maps

defined for s ≥ 1 by

(15.12.1)

for all tensors ℬ in and all vectors v ₁, …, v _s in T _p (M). Pullback by F (for covariant tensor fields) is the family of linear maps

defined for s ≥ 1 by

(15.12.2)

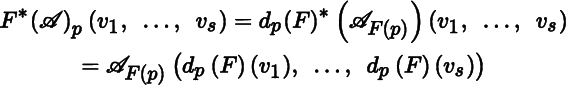
for all tensor fields in , all points p in M , and all vectors v ₁, …, v _s in T _p (M), where the second equality follows from setting in (15.12.1).

We refer to F ^*(A) as the pullback of by F .

To give meaning to F ^* when s = 0, recall from (15.6.3) that . We therefore define

for all functions g in C ^∞(N) and all p in M ; that is, we define

(15.12.3)

Since , part (b) of Theorem 15.12.1 follows from part (c). Identity (15.12.3) has several implications: Theorem 15.9.2 follows from Theorem 15.12.1(d); the identity in Theorem 15.10.4 can be expressed as

for all vector fields Y in and all functions g in C ^∞(N); Theorem 15.11.1(b) follows from Theorem 15.12.1(b); and (15.11.4) can be expressed as

for all functions g in C ^∞(N).

15.13 Pullback of Differential Forms

Let M and N be smooth manifolds, and let F : M → N be a smooth map. In Section 15.12, we defined F ^* : , the pullback by F for covariant tensor fields. We seek a corresponding pullback for differential forms. An observation is that Λ ^s (M) is a subspace of , Λ ^s (N) is a subspace of , and F ^*(Λ ^s (N)) is a subspace of Λ ^s (M), so we can proceed by restricting the maps defined in (15.12.1)–(15.12.3). Pullback by F (for differential forms) is the family of linear maps

defined for s ≥ 1 by

for all differential forms ω in Λ ^s (N), all points p in M , and all vectors v ₁, …, v _s in T _p (M). We refer to F ^*(ω) as the pullback of ω by F . As before, when s = 0, we define F ^* = F ^• .

15.14 Contraction of Tensor Fields

This brief section presents the manifold versions of several of the results in Section 5.4.