Chapter 2
Matrices and Determinants
In this chapter, we review some of the basic results from the theory of matrices and determinants.
2.1 Matrices
Let us denote by Mat m × n the set of m × n matrices (that is, m rows and n columns) with real entries. When m = n , we say that the matrices are square. It is easily shown that with the usual matrix addition and scalar multiplication, Mat m × n is a vector space, and that with the usual matrix multiplication, Mat m × m is a ring.
Let P be a matrix in Mat m × n , with

The transpose of P is the matrix P T in Mat n × m defined by

The row matrices of P are
and the column matrices of P are

We say that a matrix ![]() in Mat
m × m
is symmetric if
Q = Q
T
, and diagonal if
in Mat
m × m
is symmetric if
Q = Q
T
, and diagonal if ![]() for all
i ≠ j
. Evidently, a diagonal matrix is symmetric. Given a vector (a
1, … , a
m
) in ℝ
m
, the corresponding diagonal matrix is defined by
for all
i ≠ j
. Evidently, a diagonal matrix is symmetric. Given a vector (a
1, … , a
m
) in ℝ
m
, the corresponding diagonal matrix is defined by
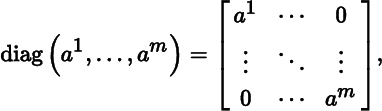
where all the entries not on the (upper‐left to lower‐right) diagonal are equal to 0. For example,

The zero matrix in Mat m × n , denoted by O m × n , is the matrix that has all entries equal to 0. The identity matrix in Mat m × m is defined by
so that, for example,

We say that a matrix Q in Mat m × m is invertible if there is a matrix in Mat m × m , denoted by Q –1 and called the inverse of Q, such that
It is easily shown that if the inverse of a matrix exists, then it is unique.
Multi‐index notation, introduced in Appendix A, provides a convenient way to specify submatrices of matrices. Let 1 ≤r ≤ m
and 1 ≤s ≤ n
be integers, and let
I = (i
1, … , i
r
) and
J = (j
1, … , j
s
) be multi‐indices in ![]() and
and ![]() respectively. For a matrix
respectively. For a matrix ![]() in Mat
m × n
, we denote by
in Mat
m × n
, we denote by

the r × s submatrix of P consisting of the overlap of rows i 1, i 2, … , i r and columns j 1, j 2, … , j s (in that order); that is,

When r = m , in which case (i 1, … , i m ) = (1, … , m), we denote

and when s = n , in which case (j 1, … , j n ) = (1, … , n), we denote
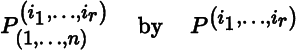
When r = 1, so that I = (i) for some 1 ≤ i ≤ m , we have
which is the ith row matrix of P. Similarly, when s = 1, so that J = (j) for some 1 ≤ j ≤ n , we have
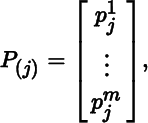
which is the jth column matrix of P.
For a matrix ![]() in Mat
m × m
, the trace of P
is defined by
in Mat
m × m
, the trace of P
is defined by

2.2 Matrix Representations
Matrices have many desirable computational properties. For this reason, when computing in vector spaces, it is often convenient to reformulate arguments in terms of matrices. We employ this device often.
Let V be a vector space, let ℋ = (h 1, … , h m ) be a basis for V, and let v be a vector in V, with
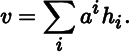
The matrix representation of v with respect to ℋ is denoted by [v]ℋ and defined by

We refer to a 1, … , a m as the components of v with respect to ℋ. In particular,

where 1 is in the ith position and 0s are elsewhere for i = 1, … , m .
With V and ℋ as above, let W be another vector space, and let ![]() be a basis for W. Let
A : V → W
be a linear map, with
be a basis for W. Let
A : V → W
be a linear map, with
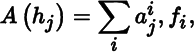
so that

for
j = 1, … , m
. The matrix representation of A
with respect to ℋ and ℱ is denoted by ![]() and defined to be the
n × m
matrix
and defined to be the
n × m
matrix
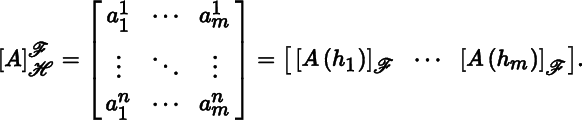
As an example, consider the linear map A : ℝ2 → ℝ3 given by A(x, y) = (y, 2x, 3x + 4), and let ℰ and ℱ be the standard bases for ℝ2 and ℝ3 , respectively. Then
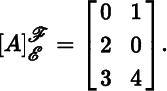
Proof
(a): By parts (a) and (b) of Theorem 2.2.2, ![]() is a linear map, and it is easily shown that
is a linear map, and it is easily shown that ![]() is injective. We claim that Mat
n × m
and Lin (V, W) both have dimension mn. Let E
ij
be the matrix in Mat
n × m
with 1 in the ij‐th position and 0s elsewhere for
i = 1, … , n
and
j = 1, … , m
. It is readily demonstrated that the E
ij
comprise a basis for Mat
n × m
, which therefore has dimension mn. Let
is injective. We claim that Mat
n × m
and Lin (V, W) both have dimension mn. Let E
ij
be the matrix in Mat
n × m
with 1 in the ij‐th position and 0s elsewhere for
i = 1, … , n
and
j = 1, … , m
. It is readily demonstrated that the E
ij
comprise a basis for Mat
n × m
, which therefore has dimension mn. Let ![]() and ℱ = (f
1 … , f
n
), and using Theorem 1.1.10, define linear maps L
ij
in Lin (V, W) by
and ℱ = (f
1 … , f
n
), and using Theorem 1.1.10, define linear maps L
ij
in Lin (V, W) by
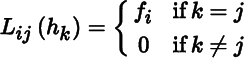
for i = 1, … , n and j = 1, … , m . Then

for all real numbers ![]() . Let B be a map in Lin (V, W), with
. Let B be a map in Lin (V, W), with ![]() . We have from (2.2.4) that
. We have from (2.2.4) that
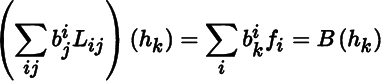
for
k = 1, … , m
. By Theorem 1.1.10,![]() , so the L
ij
span Lin (V, W). Suppose
, so the L
ij
span Lin (V, W). Suppose ![]() for some real numbers
for some real numbers ![]() , where 0 denotes the zero map in Lin (V, W). It follows from (2.2.4) that
, where 0 denotes the zero map in Lin (V, W). It follows from (2.2.4) that ![]() for
k = 1, … , m
. Since ℱ is a basis for W,
for
k = 1, … , m
. Since ℱ is a basis for W, ![]() for
i = 1, … , n
and
k = 1, … , m
, so the L
ij
are linearly independent. Thus, the L
ij
comprise a basis for Lin (V, W), and therefore, Lin (V, W) has dimension mn. This proves the claim. Suppose
for
i = 1, … , n
and
k = 1, … , m
, so the L
ij
are linearly independent. Thus, the L
ij
comprise a basis for Lin (V, W), and therefore, Lin (V, W) has dimension mn. This proves the claim. Suppose ![]() for some map A in Lin (V, W). It follows from Theorem 1.1.10, (2.2.2), and (2.2.3) that A is the zero map, hence
for some map A in Lin (V, W). It follows from Theorem 1.1.10, (2.2.2), and (2.2.3) that A is the zero map, hence ![]() . The result now follows from Theorem 1.1.12 and Theorem 1.1.14.
. The result now follows from Theorem 1.1.12 and Theorem 1.1.14.
(b) : This follows from Theorem 2.2.2(c) and part (a).
Theorem 2.2.4
Let V and W be vector spaces, let ℋ and ℱ be respective bases, let A : V → W be a linear map, and let v be a vector in V. Then
Proof
Let ℋ = (h 1, … , h m ) and v = ∑ i a i h i . It follows from (2.2.1) and (2.2.2) that
By parts (a) and (b) of Theorem 2.2.2,
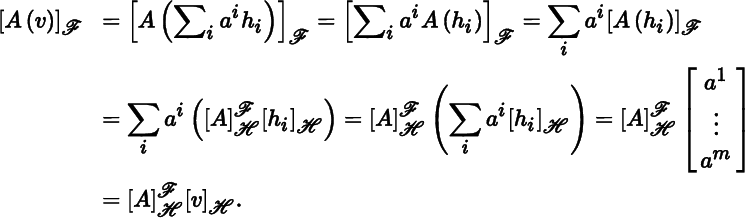
Let V be a vector space, and let ℋ and ℱ be bases for V. Setting A = id V in Theorem 2.2.4 yields
This shows that ![]() is the matrix that transforms components with respect to ℋ into components with respect to ℱ. For this reason,
is the matrix that transforms components with respect to ℋ into components with respect to ℱ. For this reason, ![]() is called the change of basis matrix from ℋ to ℱ. Let
is called the change of basis matrix from ℋ to ℱ. Let ![]() . Then (2.2.2) and (2.2.3) specialize to
. Then (2.2.2) and (2.2.3) specialize to
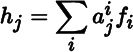
for i = 1, … , m and
Theorem 2.2.5
Let V and W be vector spaces, let ℋ and ℱ be respective bases, and let A : V → W be a linear isomorphism. Then:
Remark
By Theorem 1.1.13(a), A(ℋ) is a basis for W, so the assertion in part (a) makes sense.
Proof
- (a): Let
 , so that [(2.2.3)] [(2.2.7)]
, so that [(2.2.3)] [(2.2.7)]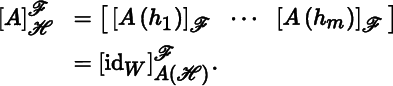
- (b) : By Theorem 2.2.2(c),
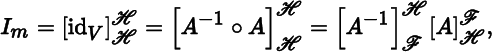
from which the result follows.
Theorem 2.2.6 (Change of Basis)
Let V be a vector space, let ℋ and ℱ be bases for V, and let A : V → V be a linear map. Then
Proof
By Theorem 2.2.2(c),
The result now follows from Theorem 2.2.5(b).
Theorem 2.2.7
Let V be a vector space, let
ℋ
and
![]() be bases for V, let Θ and
be bases for V, let Θ and
![]() be the corresponding dual bases, and let
A : V → V
be a linear map. Then
be the corresponding dual bases, and let
A : V → V
be a linear map. Then
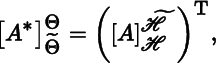
where A * is the pullback by A.
Proof
Let ℋ = (h
1, … , h
m
) and ![]() ,let Θ = (θ
1, … , θ
m
) and
,let Θ = (θ
1, … , θ
m
) and ![]() , and let
, and let ![]() . By (2.2.2) and (2.2.3),
. By (2.2.2) and (2.2.3), ![]() . Then
. Then

Again by (2.2.2) and (2.2.3), ![]()
2.3 Rank of Matrices
Consider the n‐dimensional vector space Mat1 × n of row matrices and the m‐dimensional vector space Mat m × n of column matrices. Let P be a matrix in Mat m × n . The row rank of P is defined to be the dimension of the subspace of Mat1 × n spanned by the rows of P:
Similarly, the column rank of P is defined to be the dimension of the subspace of Mat m × 1 spanned by the columns of P:
To illustrate, for
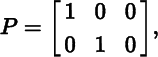
we have rowrank(P) = colrank(P) = 2. As shown below, it is not a coincidence that the row rank and column rank of P are equal.
Theorem 2.3.1
Let V and W be vector spaces, let ℋ and ℱ be respective bases, and let A : V → W be a linear map. Then
Proof
Let ℋ = (h 1, … , h m ). It follows from Theorem 2.2.1 and (2.2.3) that
for j = 1, … , m . Since ℒℱ is an isomorphism and A(h 1), … , A(h m ) span the image of A, we have

Theorem 2.3.2
If P is a matrix in Mat m × n , then
Proof
Let ℰ and ℱ be the standard bases for ℝ
n
and ℝ
m
, respectively, and let Ξ and Φ be the corresponding dual bases. Let ![]() , and let
A : ℝ
n
→ ℝ
m
be the linear map defined by
, and let
A : ℝ
n
→ ℝ
m
be the linear map defined by
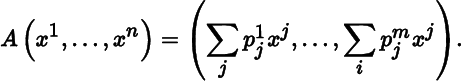
Then ![]() . By Theorem 2.3.1,
. By Theorem 2.3.1,
We have from Theorem 2.2.7 that ![]() , so a similar argument gives
, so a similar argument gives
The result now follows from Theorem 1.4.3(a).
In light of Theorem 2.3.2, the common value of the row rank and column rank of P is denoted by rank (P) and called the rank of P . Thus,
2.4 Determinant of Matrices
This section presents the basic results on the determinant of matrices.
Consider the m‐dimensional vector space Mat m × 1 of column matrices and the corresponding product vector space (Mat m × 1) m . We denote by (E 1, … , E m ) the standard basis for Mat m × 1 , where E j has 1 in the jth row and 0s elsewhere for j = 1, … , m . Let
be an arbitrary function, and let σ be a permutation in S m , the symmetric group on {1, 2, … , m}.We define a function
by
for all matrices P 1, … , P m in Mat m × 1 .
Theorem 2.4.1
If Δ :
(Mat
m × 1)
m
→ ℝ
is a function, and σ and ρ are permutations in
![]() , then
, then
Proof
Setting P σ(1) = Q 1, … , P σ(m) = Q m we have
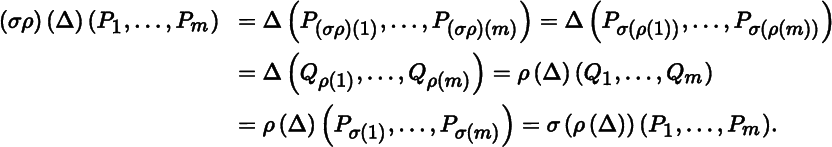
Since P 1, … , P m were arbitrary, the result follows.
A function Δ : (Mat m × 1) m → ℝ is said to be multilinear if for all matrices P 1, … , P m , Q in Mat m × 1 and all real numbers c,
for i = 1, … , m . We say that Δ is alternating if for all matrices P 1, … , P m in Mat m × 1 ,
for all 1 ≤ i < j ≤ m
. Equivalently, Δ is alternating if
τ(Δ) = − Δ for all transpositions
τ
in ![]() .
.
Theorem 2.4.1
If Δ : (Mat m × 1) m → ℝ is a multilinear function, then the following are equivalent:
- Δ is alternating.
-
σ(Δ) = sgn(σ)Δ for all permutations a in
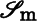 .
. - If P 1, … , P m are matrices in Mat m × 1 and two (or more) of them are equal, then Δ(P 1, … , P m ) = 0.
- If P 1, … , P m are matrices in Mat m × 1 and Δ(P 1, … , P m ) ≠ 0, then P 1, … , P m are linearly independent.
Proof
(a) ⇒(b) : Let σ = τ 1⋯τ k be a decomposition of σ into transpositions. By Theorem 2.4.1,
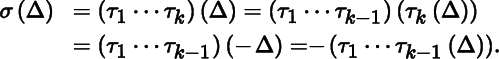
Repeating the process k – 1 more times gives σ(Δ) = (−1) k Δ. By Theorem B.2.3,sgn(σ) = (−1) k .
(b) ⇒ (a) : If Τ is a transposition in ![]() , then, by Theorem B.2.3,
τ(Δ) = sgn(τ)Δ = − Δ.
, then, by Theorem B.2.3,
τ(Δ) = sgn(τ)Δ = − Δ.
(a) ⇒ (c) : If P i = P j for some 1 ≤ i < j ≤ m , then
On the other hand, since Δ is alternating,
Thus,
from which the result follows.
(c) ⇒ (a) : For 1 ≤ i < j ≤ m . we have

from which the result follows.
To prove (c) ⇒ (d), we replace the assertion in part (d) with the following logically equivalent assertion:
(d′) : If P 1, … , P m are linearly dependent matrices in Mat m × 1 , then Δ(P 1, … , P m ) = 0.
(c) ⇒ (d′) : Since
P
1, … , P
m
are linearly dependent, one of them can be expressed as a linear combination of the others, say, ![]() . Then
. Then

Since Δ(P i , P 2, … , P m ) has P i in (at least) two positions, Δ(P i , P 2, … , P m ) = 0 for i = 2, … , m . Thus, Δ(P 1, … P m ) = 0.
(d′) ⇒ (c): If two (or more) of P 1, … , P m are equal, then P 1, … , P m are linearly dependent, so Δ(P 1, … P m ) = 0.
A function Δ : (Mat m × 1) m → ℝ is said to be a determinant function (on Mat m × 1 ) if it is both multilinear and alternating.
Theorem 2.4.3
Let Δ : (Mat m × 1) m → ℝ be a determinant function, and let P 1, … , P m be matrices in Mat m × 1 , with

Then
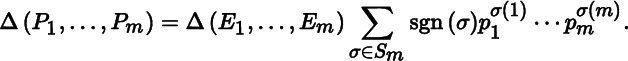
Proof
We have
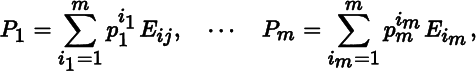
hence

Theorem 2.4.4 (Existence of Determinant Function)
There is a unique determinant function
on Mat m × 1 such that det(E 1, … E m ) = 1 . More specifically,

for all matrices P 1, … , P m P1,..., P m in Mat m × 1 , where

Proof
Let us begin by showing that the right‐hand sides of (2.4.1) are equal. We have
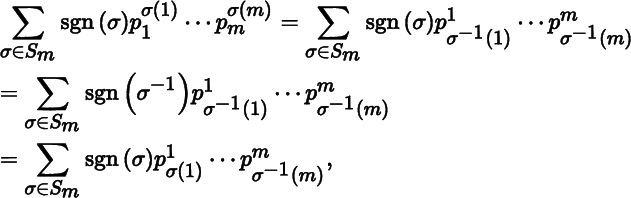
where the second equality follows from Theorem B.2.2(b), and the third equality from the observation that as σ varies over S m so does σ –1.
Existence
With P 1, … , P m as above, define a function det : (Mat m × n ) m → ℝ using the first equality in (2.4.1). It is easily shown that det is multilinear. For a given permutation ρ in S m we have

hence
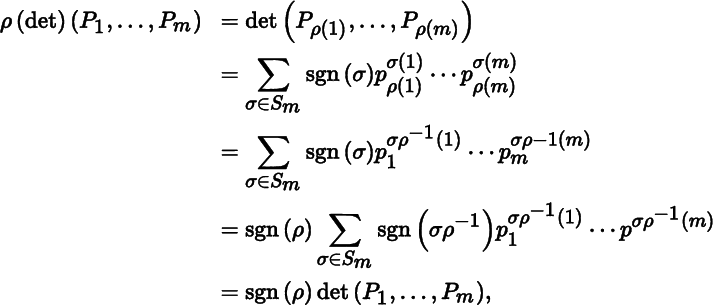
where the fourth equality follows from Theorem B.2.2, and the last equality follows from the observation that as σ varies over S m , so does σρ –1. Since P 1, … , P m were arbitrary, ρ(det) = sgn(ρ)det. By Theorem 2.4.2, det is alternating. Thus, det is a determinant function. A straightforward computation shows that det(E 1, … , E m ) = 1.
Uniqueness
This follows from Theorem 2.4.3.
Let P be a matrix in Mat m × m , and recall that in multi‐index notation the column matrices of P are P (1), … , P (m) . Setting
we henceforth view P as an m‐tuple of column matrices. In this way, the vector spaces Mat m × m and (Mat m × 1) m are identified. Accordingly, we now express the determinant function in Theorem 2.4.4 as
so that
where det (P) is referred to as the determinant of P. In particular, the condition det(E 1, … E m ) = 1 in Theorem 2.4.4 becomes
Theorem 2.4.5
If P and Q are matrices in Mat m × m , then:
- det(PQ) = det(P) det(Q).
- If P is invertible, then det(P −1) = det(P)−1.
- det(P)T = det(P).
Proof
(a): Let us define a function A : Δ : (Mat m × 1) m → ℝ by
for all matrices R 1, … , R m in Mat m × 1 . It is easily shown that Δ is a determinant function. We have
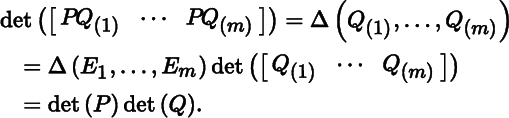
(b): We have from (2.4.1) and part (a) that
from which the result follows.
(c): Let ![]() . Then
. Then

where the first and last equalities follow from (2.4.1), and the second equality from the observation that ![]() for all permutations σ in S
m
.
for all permutations σ in S
m
.
Let P be a matrix in Mat m × m . The ij‐th cofactor of P is defined by
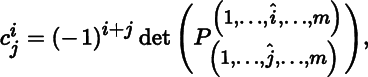
where ^ indicates that an expression is omitted. Thus, 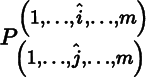 is the matrix in Mat(m − 1) × (m − 1)
obtained by deleting the ith row and jth column of P. The adjugate of P
is the matrix in Mat
m × m
defined by
is the matrix in Mat(m − 1) × (m − 1)
obtained by deleting the ith row and jth column of P. The adjugate of P
is the matrix in Mat
m × m
defined by
Theorem 2.4.6 (Column Expansion of Determinant)
If
![]() is a matrix in
Mat
m × m
and
1 ≤ j ≤ m
, then
is a matrix in
Mat
m × m
and
1 ≤ j ≤ m
, then
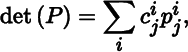
which is called the expansion of det(P) along the jth column of P.
Proof
We have
hence
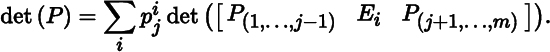
We also have

where the second equality is obtained by switching i – 1 adjacent rows, and then switching j – 1 adjacent columns, and where the fourth equality follows from (2.4.1). Combining the above identities gives the result.
Theorem 2.4.7
If P is a matrix in Mat m × m , then
Proof
Let ![]() . For given integers 1 ≤ k
,
l ≤ m
1, let
. For given integers 1 ≤ k
,
l ≤ m
1, let ![]() be the matrix in Mat
m × m
obtained by replacing the kth column of P with the lth column of P; that is,
be the matrix in Mat
m × m
obtained by replacing the kth column of P with the lth column of P; that is,
Let ![]() and
and ![]() . By Theorem 2.4.6,
. By Theorem 2.4.6,

If k ≠ l , then two columns of Q are equal and

It follows from Theorem 2.4.2 and Theorem 2.4.6 that

Thus,
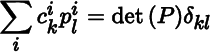
for k,
l = 1, … , m, where δ
kl
is Kronecker’s delta. Then ![]() Taking transposes gives the result.
Taking transposes gives the result.
Theorem 2.4.8
If P is a matrix in Mat m × m , then the following are equivalent:
- P is invertible.
- det(P) ≠ 0.
- rank(P) = m.
If any of the above equivalent conditions is satisfied, then

Proof
(a) ⇒ (b): By Theorem 2.4.5(b), det(P) det(P −1) = 1, hence det(P) ≠ 0.
(b) ⇒ (c): Since ![]() it follows from Theorem 2.4.2 that
P
(1), … , P
(m)
are linearly independent, so
it follows from Theorem 2.4.2 that
P
(1), … , P
(m)
are linearly independent, so
(c) ⇒ (a): Since ![]() is a basis for Mat
m × 1
. Let
is a basis for Mat
m × 1
. Let ![]() . By definition,
E
j
= P[E
j
]ℙ
for
j = 1, … , m, hence
. By definition,
E
j
= P[E
j
]ℙ
for
j = 1, … , m, hence
so Q = P –1.
The final assertion follows from Theorem 2.4.7.
Theorem 2.4.9
The matrices
P
1, … , P
m
in
Mat
m × 1
are linearly independent if and only if
![]()
Proof
We have
P 1, … , P m are linearly independent

The next result is not usually included in an overview of determinants, but it will prove invaluable later on.
Theorem 2.4.10 (Cauchy–Binet Identity)
Let 1 ≤ k ≤ m be integers.
-
If P and Q are matrices in
Mat
m × k
, then

-
If R and S are matrices in
Mat
k × m
, then

Proof
(a): Let ![]() , so that
, so that
and
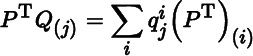
for j = 1, … , k. We have

where the third equality follows from Theorem 2.4.2. The term in large parentheses in the last row of the preceding display can be expressed as
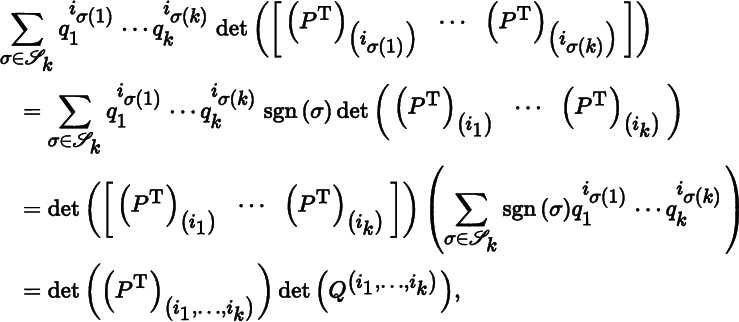
where the first equality follows from Theorem 2.4.2, and the third equality from (2.4.1). Then

(b): We have
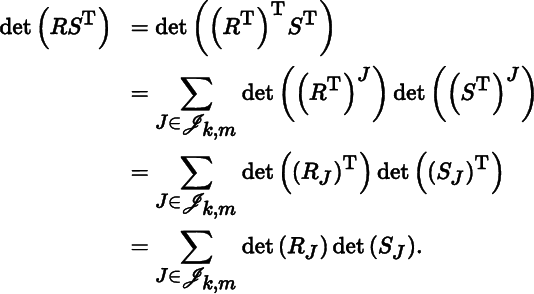
Example 2.4.11 (Classical Cauchy–Binet Identity)
Let P and Q be matrices in Mat m × 2 , with

Then

and

By Theorem 2.4.10(a),
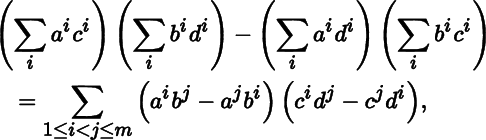
which is the classical version of the Cauchy–Binet identity.
Theorem 2.4.12
If V is a vector space, and ℋ and ℱ are bases for V, then
Proof
We have

from which the result follows.
It was remarked in connection with Theorem 2.2.3 that Mat m × m is a ring under the usual operations of matrix addition and matrix multiplication, hence it is a group under matrix addition. But Mat m × m is clearly not a group under matrix multiplication because not all matrices have an inverse. However, Mat m × m contains a number of matrix groups. The largest of these is the general linear group, consisting of all invertible matrices:
where the characterization using determinants follows from Theorem 2.4.8.
We say that a matrix P in Mat m × m is orthogonal if P T P = I m . If so, then P T = P −1, hence P P T = P P −1 = I m . Thus, P T P = I m if and only if P P T = I m . The orthogonal group is the subgroup of GL (m) consisting of all orthogonal matrices:
For a matrix P in O (m), we have
hence det(P) = ± 1. The special orthogonal group is the subgroup of O (m) consisting of all matrices with determinant equal to 1:
2.5 Trace and Determinant of Linear Maps
The trace and determinant of a matrix were defined in Section 2.1 and Section 2.4, respectively. We now extend these concepts to linear maps.
Let V be a vector space, let ℋ be a basis for V, and let A : V → V be a linear map. The trace of A is defined by
and the determinant of A by
Theorem 2.5.1
With the above setup, tr(A) and det(A) are independent of the choice of basis for V.
Proof
Let ℱ be another basis for V. By Theorem 2.2.6,
We have from Theorem 2.1.7(c) that
and from Theorem 2.4.5 that
Theorem 2.5.2
If V is a vector space and A, B : V → V are linear maps, then:
- det(id V ) = 1.
- det(A ∘ B) = det(A) det(B).
- If A is a linear isomorphism, then det(A −1) = det(A)−1.
- det(A *) = det(A).
Proof
- (a): This follows from Theorem 2.2.3(b) and (2.4.2).
- (b): This follows from Theorem 2.2.3(b) and Theorem 2.4.5(a).
- (c): This follows from Theorem 2.2.3(b) and Theorem 2.4.5(b).
- (d): This follows from Theorem 2.2.7 and Theorem 2.4.5(c).
Theorem 2.5.3
Let V be a vector space, and let A : V → V be a linear map. Then A is a linear isomorphism if and only if det(A) ≠ 0.
Proof
This follows from Theorem 2.2.3(b) and Theorem 2.4.8.

