Appendix A
Notation and Set Theory
In this appendix, we recall some of the elements of set theory.
Let X be a set, and let S 1 and S 2 be subsets of X. We say that S 1 and S 2 intersect or overlap if S 1 ∩ S 2 ≠ ∅, and that they do not intersect, do not overlap, or are disjoint if S 1 ∩ S 2 = ∅, where ∅ denotes the empty set. The difference between S 1 and S 2 (in that order) is the set
Let {S α : α ∈ A} be a collection of subsets of X, where A is some indexing set. The union and intersection of the S α are denoted by
respectively. The (Cartesian) product of sets X 1, …, X n is defined by
and each (x 1, …, x n ) is called an n‐tuple. For a set X, we denote X × ⋯ × X [n copies] by X n .
Let F : X → Y be a map. (The term “function” is reserved for a special type of map, as discussed below.) We refer to X and Y as the domain of F and codomain of F , respectively. The image of F is denoted by im (F) or F(X) and defined by
It is implicit in the notation F : X → Y that F(X) is defined for all x in X. On the other hand, F(X) may be a proper subset of Y. Let T be a subset of Y, and define
Observe that we do not require T to be a subset of F(X). Thus,
If there is an element y 0 in Y such that F(x) = y 0 for all x in X, then F is said to be constant or to have constant value. This is sometimes expressed as F = y 0 . We say that F is injective if distinct elements of X are mapped to distinct elements of Y; that is, if x 1 and x 2 are elements of X such that F(x 1) = F(x 2), then x 1 = x 2 . We say that F is surjective or onto if every element of Y is the image of some element of X; that is, F(X) = Y . A map that is both injective and surjective is called bijective.
The restriction of F : X → Y to a subset S of X is the map denoted by
and defined by F| S (x) = F(x) for all x in S. It is sometimes convenient to use the notation F ∣ S instead of F ∣ s , especially when S is a complicated expression. Given a map G : Y → Z , the composite of G and F is the map denoted by
and defined by
for all x in X. Observe that we do not require F to be surjective, so that G ∘ F(X) might be a proper subset of G(Y).
The identity map
is defined by id X (x) = x for all x in X.
Let F : X → Y 1 × ⋯ × Y n be a map, and for each x in X, let us express F(x) as
This defines maps F i : X → Y i for i = 1, …, n , called the component maps of F or simply the components of F . We often write
The set of real numbers is denoted by ℝ. We adopt the following convention.
Throughout, a map with the codomain ℝ is called a function.
Let f : X → ℝ be a function, and let x be an element of X. We say that f vanishes at x if f(x) = 0, is nonvanishing at x if f(x) ≠ 0, and is nowhere‐vanishing (on X) if it is nonvanishing at every x in X. We say that f is strictly positive if f(x) > 0 for all x in X, and strictly negative if f(x) < 0 for all x in X. The function f : ℝ → ℝ is said to be increasing if f(x 1) ≤ f(x 2) for all x 1 < x 2 , and strictly increasing if f(x 1) < f(x 2) for all x 1 < x 2 . Analogous definitions are given for decreasing and strictly decreasing.
Given a real number c, the constant function on X with value c, denoted by c M or simply c, is the function that sends all elements of X to c. In particular, we have 0 X , called the zero function, and 1 X .
The cardinality of a set X is denoted by card(X) and defined to be the number of elements in the set, which is either finite or infinite. Two sets are said to have the same cardinality if there is a bijective map between them. It is known that there are different types of “infinity” For instance, we say that a set is countable if it has the same cardinality as the positive integers. It can be shown that the rational numbers are countable, but the real numbers are not.
A binary relation on a set X is a subset ~ of X × X . If (x 1, x 2) is in ~, then x 1 is said to related to x 2 , written x 1 ∼ x 2 . We say that ~ is an equivalence relation on X if:
| [E1] | x ∼ x for all x in X. | (reflexivity) |
| [E2] | If x 1 ∼ x 2 , then x 2 ∼ x 1 for all x 1, x 2 in X. | (symmetry) |
| [E3] | If x 1 ∼ x 2 and x 2 ∼ x 3 , then x 1 ∼ x 3 for all x 1, x 2, x 3 in X. | (transitivity) |
If ~ is an equivalence relation on X and x is an element of X, the equivalence class determined by x is denoted by [x] and defined to be the set of elements of X that are related to x:
In particular, we have from [El] that [x] contains x .
A partition of X is a collection of disjoint nonempty subsets of X whose union equals X.
The sign of a nonzero real number x is defined by

The sign of 0 is not defined.
Kronecker's delta is the function
defined by
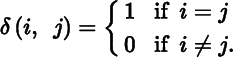
We henceforth denote
δ(i, j) by either of the equivalent expressions
δ
ij
or ![]() , the choice depending on the context.
, the choice depending on the context.
For an integer 1 ≤ k ≤ n , we say that a k‐tuple (i 1, …, i k ) of distinct elements of {1, …, n} is a multi‐index if i 1 < ⋯ < i k . The set of multi‐indices on {1, …, n} with k elements is denoted by ℐ k, n , and a typical multi‐index I in ℐ k, n is denoted by I = (i 1, …, i k ). For example,
Evidently, ℐ
k, n
has ![]() elements, where
elements, where ![]() is a binomial coefficient. The complement of the multi‐index
I = (i
1, …, i
k
) in ℐ
k, n
is the multi‐index
I
c = (i
k + 1, …, i
n
) in ℐ
n − k, n
where
is a binomial coefficient. The complement of the multi‐index
I = (i
1, …, i
k
) in ℐ
k, n
is the multi‐index
I
c = (i
k + 1, …, i
n
) in ℐ
n − k, n
where
In particular, the complement of the multi‐index (i) in ℐ1, n is the multi‐index
in ℐ
n − 1, n
for
i = 1, …, n
, where ![]() indicates that an expression is omitted. To illustrate, for (2) in ℐ1, 6
and (1, 2, 3, 6) in ℐ4, 6
, we have the complements (2)c = (1, 3, 4, 5, 6) in ℐ5, 6
and (1, 2, 3, 6)c = (4, 5) in ℐ2, 6
.
indicates that an expression is omitted. To illustrate, for (2) in ℐ1, 6
and (1, 2, 3, 6) in ℐ4, 6
, we have the complements (2)c = (1, 3, 4, 5, 6) in ℐ5, 6
and (1, 2, 3, 6)c = (4, 5) in ℐ2, 6
.
