It is not unusual in practice to encounter what would otherwise be a smooth manifold except for the presence of some type of “boundary” In this chapter, we introduce smooth manifolds with boundary and prove one of most important results in differential geometry—Stokes's theorem.

17.1 Smooth Manifolds with Boundary

The closed upper half‐space of ℝ ^m , defined by

is the model for what we later call a smooth m‐manifold with boundary. It is easily shown that

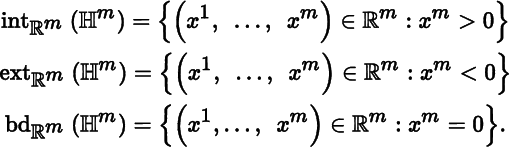
For example, ℍ³ = {(x,  y,  z) ∈ ℝ³ : z ≥ 0} is the upper half of ℝ³ including the xy‐plane, is the upper half of ℝ³ excluding the xy‐plane, is the lower half of ℝ³ excluding the xy‐plane, and is the xy‐plane.

Throughout, ℍ ^m is assumed to have the subspace topology induced by ℝ ^m .

Our first goal is to use ℍ ^m to broaden our earlier notion of “chart” Let M be a topological space, and consider the following modification of the definition of chart given in Section 14.1. A chart on M is a pair (U,  φ), where U is an open set in M and φ : U → ℍ ^m is a map such that:

[C1] φ(U) is an open set in ℍ ^m .

[C2] φ : U → φ(U) is a homeomorphism.

The difference from the earlier formulation is that ℍ ^m appears in [Cl] instead of ℝ ^m We refer to m as the dimension of the chart. For each point p in φ(U), (U, φ) is said to be a chart at p . As before, an atlas for M is a collection of charts on M such that the U _α form an open cover of M.

A topological m‐manifold with boundary is a pair , where M is a topological space and is an atlas for M such that:

[T1] Each chart in has dimension m.

[T2] The topology of M has a countable basis.

[T3] For every pair of distinct points p ₁, p ₂ in M, there are disjoint open sets U ₁ and U ₁ in M such that p ₁ is in U ₁ and p ₂ is in U ₂.

Let M be a topological m‐manifold with boundary, and let (U, φ) be a chart on M. We say that (U,  φ) is an interior chart if φ(U) is contained in , and a boundary chart if φ(U) intersects . Evidently, any chart on M is either an interior chart or a boundary chart. Since is an open set in ℝ ^m , it follows from Theorem 9.1.5 that if (U,  φ) is an interior chart, then it is a chart in the sense of Section 14.1. On the other hand, if φ(U) intersects , we have something entirely new.

Let p be a point in M. We say that p is an interior point of M if there is a chart (U,  φ) at p such that φ(p) is in , and that p is a boundary point of M if there is a chart (V,  ψ) at p such that ψ(p) is in . See Figure 17.1.1, where p ₁ and p ₂ are interior points, and p ₃ is a boundary point. We observe that a chart at an interior point is either an interior chart or a boundary chart, but a chart at a boundary point is necessarily a boundary chart. Since any point p in M is contained in at least one chart, it is either an interior point (with respect to that chart) or a boundary point (with respect to that chart). This raises the question of whether p can be an interior point with respect to one chart, and at the same time a boundary point with respect to another chart. It is a crucial fact that this cannot happen.

Let M be a topological manifold with boundary, and let p be a point in M. A consequence of Theorem 17.1.1 is that determining whether p is an interior point or a boundary point is independent of the choice of chart at p. The set of interior points of M is denoted by M ^o and called the (manifold) interior of M , and the set of boundary points of M is denoted by ∂M and called the (manifold) boundary of M . Thus, M is the disjoint union of M° and ∂M.

With the notion of chart in hand, the other core definitions presented in Section 14.1—transition map, tangent space, smooth atlas, and so on—transfer to the present setting virtually word for word. However, the boundary of ℍ ^m must be taken into account. To that end, when smoothness is being considered, we adopt the “extended” definition of smoothness introduced in Section 10.1.

A topological manifold with boundary is said to be a smooth m‐manifold with boundary if is a smooth atlas for M.

Let M be a smooth manifold with boundary, let (U,  φ) be a boundary chart on M, and let p be a point in ∂M ∩ U . By definition, p is a boundary point, so we have from Theorem 17.1.1 that φ(p) is in ∂ℍ ^m . Thus, a coordinate map sends boundary points to boundary points. More generally, we have the following result.

There is nothing in the definition of a smooth manifold with boundary that requires the boundary to be nonempty. If the boundary is in fact empty, then the smooth atlas is comprised entirely of interior charts. In that case, the resulting smooth structure is that of a smooth manifold as defined in Section 14.1. For this reason, a smooth manifold with boundary where the boundary is empty will be referred to simply as a smooth manifold. On the other hand, we establish the following convention.

Henceforth, a smooth manifold with boundary is assumed to have a nonempty boundary.

The definition of submanifold given in Section 14.8 generalizes immediately to the present setting. A submanifold of either a smooth manifold or a smooth manifold with boundary might or might not have a boundary. We use the terms submanifold and submanifold with boundary as necessary to clarify the situation. For example, ℍ ^m is an m‐submanifold with boundary of the smooth m manifold ℝ ^m When dealing with either a smooth manifold or a smooth manifold with boundary, we employ the term chart in a generic sense to refer to either an interior chart or a boundary chart, reserving the latter terminology for situations where the difference needs to be made explicit.

The distinction between a manifold boundary and a topological boundary deserves emphasis. Consider, for example, the unit open disk D in ℝ² Viewed as an open 2‐submanifold of the smooth 2‐manifold ℝ² , D is a smooth 2‐manifold in its own right, and as such has no boundary. On the other hand, viewed as a subset of the topological space ℝ² , D has the topological boundary consisting of the unit circle.

According to the next result, the boundary of a smooth manifold with bound‐ ary automatically has a smooth structure.

As an example, ∂ℍ ^m is a hypersurface of ℍ ^m It is sometimes convenient to identify the smooth (m − 1) manifolds ∂ℍ ^m and ℝ ^m − 1 .

17.2 Inward‐Pointing and Outward‐Pointing Vectors

For a boundary point of a smooth manifold with boundary, there are two associated tangent spaces, and they need to be distinguished. Let M be a smooth m‐manifold with boundary, and let p be a point in M. It follows from the definitions given above that T _p (M) is an m‐dimensional vector space, and this is so whether p is an interior point or a boundary point. However, when p is a boundary point, we have from Theorem 17.1.5 that ∂M is a hypersurface of M, hence T _p (∂M) is an (m − 1)‐dimensional vector space. It follows from (14.8.1) and Theorem 17.1.5 that T _p (∂M) is (or at least can be identified with) a subspace of T _p (M).

Continuing with the above notation, we say that v is inward‐pointing if a ^m > 0, and outward‐pointing if a ^m < 0. According to Theorem 17.2.1, this determination is independent of the choice of chart used to express v in local coordinates. We need to consider the case a ^m = 0. It follows from Theorem 14.8.3(b) and Theorem 17.1.5 that there is a (boundary) chart on M at p that is a slice chart for ∂M in M. If (U,  φ =  (x ¹,   … ,  x ^m )) is such a chart, then ((∂/∂x ¹)| _p ,   … ,  (∂/∂x ^m − 1)| _p ) is a basis for T _p (∂M). Thus, a ^m  = 0 if and only if v is in T _p (∂M). This observation along with Theorem 17.2.1 proves the following result.

See Figure 17.2.1, where v ₁ is inward‐pointing, v ₂ is outward pointing, and v ₃ is in T _p (∂M).

Recall from Section 15.1 that is the set of smooth vector fields along ∂M . Let V be a vector field in . By definition, V _p is in T _p (M) for all p in ∂M . We say that V is inward‐pointing (outward‐pointing) if V _p is inward‐pointing (outward‐pointing) for all p in ∂M . Suppose V is in fact either inward‐pointing or outward‐pointing. According to the definition given in Section 15.1, V is nowhere‐tangent to ∂M ; or equivalently, V _p is in T _p (M)T _p (∂M) for all p in ∂M .

The “construction” in the preceding example generalizes to an arbitrary smooth manifold with boundary, as we now show.

17.3 orientation of Boundaries

Let (M, O) be an oriented smooth m‐manifold with boundary, where m ≥ 2. By Theorem 17.2.5, there is an outward‐pointing vector field V in . Let be the orientation of ∂M induced by V, as given by Theorem 16.6.9. We refer to as the Stokes orientation of ∂M . It was remarked in connection with Theorem 16.6.9 that the orientation of a hypersurface induced by a nowhere‐tangent vector field is not independent of the choice of nowhere‐tangent vector field. Here the hypersurface is a boundary and the nowhere‐tangent vector field is outward‐pointing. This added specificity has the following implication.

17.4 Stokes's Theorem

In this section, we prove one of the central results of differential geometry—Stokes's theorem. In one sweeping statement it unifies numerous core theorems of vector calculus, as illustrated in Section 21.2.

Although details will not be presented here, the theory of integration of differential forms on smooth manifolds given in Section 16.7 can be extended to include the integration of differential forms on smooth manifolds with boundary.

We will see several applications of Stokes's theorem in Section 21.2.