4.3Convex risk measures on L ∞

For the next four sections, we fix a probability measure P on (Ω,F) and consider risk measures ρ such that

In the present section, only the nullsets of P will matter.

Lemma 4.32. Let ρ be a convex risk measure that satisfies (4.33) and which is represented by a penalty function α as in (4.17). Then α(Q) = +∞ for any Q ∈ M1,f (Ω,F) which is not absolutely continuous with respect to P.

Proof. If Q ∈ M1,f (Ω,F) is not absolutely continuous with respect to P, then there exists A ∈ F such that Q[ A ] > 0 but P[ A ] = 0. Take any X ∈ Aρ, and define Xn := X − n A . Then ρ(Xn) = ρ(X), i.e., Xn is again contained in Aρ. Hence,

as n ↑ ∞.

In view of (4.33), we can identify X with the Banach space L∞ := L∞(Ω,F, P). Let us denote by

the set of all probability measures on (Ω,F) which are absolutely continuous with respect to P. The following theorem characterizes those convex risk measures on L∞ that can be represented by a penalty function concentrated on probability measures, and hence on M1(P), due to Lemma 4.32.

Theorem 4.33. Suppose ρ : L∞ → ℝ is a convex risk measure. Then the following conditions are equivalent.

(a) ρ can be represented by some penalty function on M1(P).

(b) ρ can be represented by the restriction of the minimal penalty function αmin to M1(P):

(c) ρ is continuous from above: If Xn ↘ X P-a.s. then ρ(Xn) ↗ ρ(X).

(d) ρ has the following Fatou property: for any bounded sequence (Xn) which converges P-a.s. to some X,

(e) ρ is lower semicontinuous for the weak∗ topology σ(L∞, L1).

(f) The acceptance set Aρ of ρ is weak∗ closed in L∞, i.e., Aρ is closed with respect to the topology σ(L∞, L1).

Proof. The implication (b)⇒(a) is obvious, and (a)⇒(c)⇔(d) follows as in Lemma 4.21, replacing pointwise convergence by P-a.s. convergence.

(c)⇒(e):We have to show that C := {ρ ≤ c} is weak∗ closed for c ∈ ℝ. To this end, let If (Xn) is a sequence in Cr converging in L1 to some random variable X, then there is a subsequence that converges P-a.s., and the Fatou property of ρ implies that X ∈ Cr. Hence, Cr is closed in L1, and Lemma A.68 implies that C := {ρ ≤ c} is weak∗ closed.

(e)⇒(f) is obvious.

(f)⇒(b): We fix some X ∈ L∞ and let

In view of Theorem 4.16, we need to show that m ≥ ρ(X) or, equivalently, that m + X ∈ Aρ. Suppose by way of contradiction that m + X / ∈ Aρ. Since the nonempty convex set Aρ is weak∗ closed by assumption, we may apply Theorem A.60 in the locally convex space (L∞, σ(L∞, L1)) with C := Aρ and B := {m + X }.We obtain a continuous linear functional on (L∞, σ(L∞, L1)) such that

By Proposition A.62, is of the form (Y) = E[ YZ ] for some Z ∈ L1. In fact, Z ≥ 0. To show this, fix Y ≥ 0 and note that ρ(λY) ≤ ρ(0) for λ ≥ 0, by monotonicity. Hence λY + ρ(0) ∈ Aρ for all λ ≥ 0. It follows that

Taking λ ↑ ∞yields that (Y) ≥ 0 and in turn that Z ≥ 0. Moreover, P[ Z > 0 ] > 0 since is nonzero. Thus,

defines a probability measure Q0 ∈ M1(P). By (4.36), we see that

However,

in contradiction to (4.35). Hence, m + X must be contained in Aρ, and thus m ≥ ρ(X).

The theorem shows that any convex risk measure on L∞ that is continuous from above arises in the following manner. We consider any probabilistic model Q ∈ M1(P), but these models are taken more or less seriously as described by the penalty function. Thus, the value ρ(X) is computed as the worst case, over all models Q ∈ M1(P), of the expected loss EQ[ −X ], but reduced by α(Q). In the following example, the given model P is the one which is taken most seriously, and the penalty function α(Q) is proportional to the deviation of Q from P, measured by the relative entropy.

Example 4.34. Consider the penalty function α : M1(P) → (0,∞] defined by

where β > 0 is a given constant and

is the relative entropy of Q ∈ M1(P) with respect to P; see Definition 3.20. The corresponding entropic risk measure ρβ is given by

The variational principle for the relative entropy as stated in Lemma 3.29 shows that

and that the upper bound is attained by the measure with the density e−βX/E[ e−βX ]. Thus, the entropic risk measure takes the form

Note that α is in fact the minimal penalty function representing ρβ, since Lemma 3.29 implies

A financial interpretation of the entropic risk measure in terms of shortfall risk will be discussed in Example 4.114.

◊

Exercise 4.3.1. Show that the entropic risk measure ρβ converges to the worst-case risk measure for β ↑ ∞and to the expected loss under P for β ↓ 0.

◊

Exercise 4.3.2. Show that the entropic risk measure ρβ is not coherent for any β ∈ (0,∞). To this end, take any X ∈ X that has positive expectation but carries some downside risk, that is, E[ X ] > 0 and P[ X < 0 ] > 0. Show that λX is acceptable for small enough λ > 0, but not acceptable for large λ. Thus, the acceptance set Aρβ is not a cone.

◊

The following corollary characterizes those convex risk measures on L∞ that satisfy the property of continuity from below, which is stronger than continuity from above.

Corollary 4.35. For a convex risk measure ρ on L∞, the following conditions are equivalent.

(a) ρ is continuous from below:

(b) ρ satisfies the Lebesgue property: whenever (Xn) is a bounded sequence in L∞ which converges P-a.s. to X.

(c) The minimal penalty function αmin is concentrated on M1(P), i.e., αmin(Q) < ∞ implies Q ∈ M1(P).

In particular we have

whenever one of these three equivalent conditions is satisfied.

Proof. The equivalence of conditions (a) and (b) was shown in Exercise 4.2.3. The equivalence of conditions (a) and (c) as well as (4.37) follow from Theorem 4.22 and Lemma 4.32.

Exercise 4.3.3. Show that the three conditions in Corollary 4.35 are equivalent to the following fourth condition.

(d) For each c ∈ ℝ, the level set Λc := {Q | αmin(Q) ≤ c} is contained in M1(P) and the corresponding set of densities,

is weakly compact in L1(Ω,F, P).

Hint: Use Lemma 4.23 and the Dunford-Pettis theorem (Theorem A.70).

◊

Example 4.36. Let g : [0,∞[→ ℝ ∪{+∞} be a lower semicontinuous convex function satisfying g(1) < ∞ and the superlinear growth condition g(x)/x → +∞ as x ↑ ∞. Associated with it is the g-divergence

The g-divergence Ig(Q|P) quantifies the deviation of the hypothetical model Q from the reference measure P. Thus,

is a natural choice for a penalty function. The resulting risk measure

is sometimes called divergence risk measure. Note that, for g(x) = x log x, ρg is just the entropic risk measure discussed in Example 4.34. Divergence risk measures will be discussed in more detail in Section 4.9.

◊

Exercise 4.3.4. Show that the risk measure in (4.39) is continuous from below and that αg(Q) = Ig(Q|P), Q ∈ M1(P), is its minimal penalty function. In particular, the supremum in (4.39) is in fact a maximum. Hint: Using Exercise 4.3.3 can be helpful.

◊

Theorem 4.33 takes the following form for coherent risk measures; the proof is the same as the one for Corollary 4.19.

Corollary 4.37. A coherent risk measure on L∞ can be represented by a set Q ⊂ M1(P) if and only if the equivalent conditions of Theorem 4.33 are satisfied. In this case, the maximal representing subset of M1(P) is given by

Let us also state a characterization of those coherent risk measures on L∞ which are continuous from below. It follows by combining Corollaries 4.35 and 4.37 with Exercise 4.3.3.

Corollary 4.38. For a coherent risk measure ρ on L∞ the following properties are equivalent:

(a) ρ is continuous from below:

(b) ρ satisfies the Lebesgue property: whenever (Xn) is a bounded sequence in L∞ which converges P-a.s. to X.

(c) We have Qmax ⊂ M1(P).

(d) The set of densities

is weakly compact in L1(Ω,F, P).

In this case, the representation

involves only σ-additive probability measures.

We now give three examples of coherent risk measures which will be studied in more detail in Section 4.4.

Example 4.39. In our present context, where we require condition (4.33), the worst-case risk measure takes the form

One can easily check that ρmax is coherent and satisfies the Fatou property. Moreover, the acceptance set of ρmax is equal to the positive cone Lin L∞, and this implies αmin(Q) = 0 for any Q ∈ M1(P). Thus,

Note however that the supremum on the right cannot be replaced by a maximum as soon as (Ω,F, P) cannot be reduced to a finite model. Indeed, in that case there exists X ∈ L∞ such that X does not attain its essential infimum, and so there can be no Q ∈ M1(P) such that EQ[ X ] = ess inf X = −ρmax(X). In this case, the preceding corollary shows that ρmax is not continuous from below.

◊

Example 4.40. Let Qλ be the class of all Q ∈ M1(P) whose density dQ/dP is bounded by 1/λ for some fixed parameter λ ∈ (0, 1). The corresponding coherent risk measure

will be called the Average Value at Risk at level λ. This terminology will become clear in Section 4.4, which contains a detailed study of AV@Rλ. By taking g(x) := 0 for and g(x) := +∞ for one sees that AV@Rλ falls into the class of divergence risk measures as introduced in Example 4.36. It follows from Exercise 4.3.4 that Qλ is equal to the maximal representing subset of AV@Rλ, that AV@Rλ is continuous from below, and that the supremum in (4.40) is actually attained. An explicit construction of the maximizing measure will be given in the proof of Theorem 4.52.

◊

Example 4.41. We take for Q the class of all conditional distributions P[ ·| A ] such that A ∈ F has P[ A ] > λ for some fixed level λ ∈ (0, 1). The coherent risk measure induced by Q,

is called the worst conditional expectation at level λ. We will show in Section 4.4 that it coincides with the Average Value at Risk of Example 4.40 if the underlying probability space is rich enough.

◊

Let ρ be a convex risk measure with the Fatou property. We now consider the situation in which ρ admits a representation in terms of equivalent probability measures Q ≈ P, i.e.,

We will show in the next theorem that this property can be characterized by the following concept of sensitivity, which is sometimes also called relevance. It formalizes the idea that ρ should react to every nontrivial loss at a sufficiently high level.

Definition 4.42. A convex risk measure ρ on L∞ is called sensitive with respect to P if for every nonconstant X ∈ L∞ with X ≥ 0 there exists λ > 0 such that ρ(−λX) > ρ(0).

◊

Theorem 4.43. For a convex risk measure with the Fatou property, the following conditions are equivalent.

(a) ρ admits the representation (4.42) in terms of equivalent probability measures.

(b) ρ is sensitive with respect to P.

(c) For every A ∈ F with P[ A ] > 0 there exists λ > 0 such that ρ(−λA) > ρ(0).

(d) For every A ∈ F with P[ A ] > 0 there exists Q ∈ M1(P) with Q[ A ] > 0 and αmin(Q) < ∞.

(e) There exists Q ≈ P with αmin(Q) < ∞.

Proof. Throughout the proof we will assume for simplicity that ρ is normalized in the sense that ρ(0) = 0. This can be done without loss of generality.

(a)⇒(b): Take X ∈ Lwith E [ +X ∞] > 0. By (4.42) there exists Q ≈ P with αmin(Q) < ∞and

The right-hand side is strictly positive as soon as

which is a finite number since E Q[ X ] > 0 due to Q ≈ P.

The implications “(b)⇒(c)” and “(c)⇒(d)” are both obvious.

(d) ⇒ (e): For every c > 0 the level set Λc := {Q ∈ M1(P) | αmin(Q) ≤ c} is nonempty due to our assumption ρ(0) = 0. We will show that Λc contains some Q ≈ P. We show first the following auxiliary claim:

Indeed, (d) implies that there is Q1 ∈ M1(P) with Q1[ A ] > 0 and αmin(Q1) < ∞.Now we take Q0 ∈ Λc/2 and let Qε := εQ1 + (1− ε)Q0 for 0 < ε < 1. We clearly have Qε[ A ] > 0 and

for sufficiently small ε > 0. This implies (4.43).

We now apply the Halmos–Savage theorem in the form of Theorem 1.61. It yields the existence of Q ∈ Λc with Q ≈ P ifwe can show that Λc is countably convex. To show countable convexity, let (βk)k∈N be a sequence of nonnegative real numbers summing up to 1 and take Qk ∈ Λc for k ∈ ℕ. We define Then Q ∈ M1(P) and

Thus, Q belongs to Λc, and (e) follows.

(e)⇒(a): By the representation (4.34) in Theorem 4.33 it is sufficient to show that

for any given X ∈ L∞. To this end, we take δ > 0 and choose Q0 ∈ M1(P) such that

Then we take Q1 ≈ P with αmin(Q1) < ∞, which exists due to (e). When letting Qε := εQ1 + (1 − ε)Q0 we have Qε ≈ P for all ε ∈ (0, 1) and αmin(Qε)≤ εαmin(Q1) + (1 − ε)αmin(Q0). Hence,

and the right-hand side is larger than ρ(X) − δ if ε is sufficiently small.

Condition (e) in Theorem 4.43 is of course satisfied if αmin(P) < ∞. This is the case for the worst conditional expectation WCE (Example 4.41), Average Value at Risk AV@R (Example 4.40), the divergence risk measures (Example 4.36), and in particular the entropic risk measure (Example 4.34). These, and many other risk measures, are therefore sensitive and admit a representation (4.42) in terms of equivalent risk measures.

Remark 4.44. In analogy to Remark 4.18, the implication (e)⇒(a) in the Representation Theorem 4.33 can be viewed as a special case of the general duality in Theorem A.65 for the Fenchel–Legendre transform of the convex function ρ on L∞, combined with the properties of a monetary risk measure. From this general point of view, it is now clear how to state representation theorems for convex risk measures on the Banach spaces Lp(Ω,F, P) for 1 ≤ p < ∞. More precisely, let q ∈ (1,∞] be such that and define

A convex risk measure ρ on Lp is of the form

if and only if it is lower semicontinuous on Lp, i.e., the Fatou property holds in the form

◊

4.4Value at Risk

A common approach to the problem of measuring the risk of a financial position X consists in specifying a quantile of the distribution of X under the given probability measure P. For λ ∈ (0, 1), a λ-quantile of a random variable X on (Ω,F, P) is any real number q with the property

Exercise 4.4.1. For X ∈ L1(Ω,F, P) and λ ∈ (0, 1), a real number q is a λ-quantile for X if and only if it minimizes the convex function

Hint: A minimizer q of the convex function fλ is characterized by the conditions that ( fλ)ʹ+(q) ≥ 0 and ( fλ)ʹ−(q) ≤ 0.

◊

The set of all λ-quantiles of X is an interval where

is the lower and

is the upper quantile function of X; see Appendix A.3. In this section, we will focus on the properties of viewed as a functional on a space of financial positions X.

Definition 4.45. Fix some level λ ∈ (0, 1). For a financial position X, we define its Value at Risk at level λ as

In financial terms, V@Rλ(X) is the smallest amount of capital which, if added to X and invested in the risk-free asset, keeps the probability of a negative outcome below the level λ. However, Value at Risk only controls the probability of a loss; it does not capture the size of such a loss if it occurs. Clearly, V@Rλ is a monetary risk measure on X = L0, which is positively homogeneous; see also Example 4.11. The following example shows that the acceptance set of V@Rλ is typically not convex, and so V@Rλ is not a convex risk measure. Thus, V@Rλ may penalize diversification instead of encouraging it. As a matter of fact, V@Rλ creates an incentive to concentrate risk on an event of small probability.

Example 4.46. Consider an investment into two defaultable corporate bonds, each with return > r, where r ≥ 0 is the return on a riskless investment. The discounted net gain of an investment w > 0 in the ith bond is given by

If a default of the first bond occurs with probability p ≤ λ, then

Hence,

This means that the position X1 is acceptable in the sense that is does not carry a positive Value at Risk, regardless of the possible loss of the entire investment w.

Diversifying the portfolio by investing the amount w/2 into each of the two bonds leads to the position Y := (X1 + X2)/2. Let us assume that the two bonds default independently of each other, each of them with probability p. For realistic , the probability that Y is negative is equal to the probability that at least one of the two bonds defaults: P[ Y < 0] = p(2 − p). If, for instance, p = 0.009 and λ = 0.01 then we have p < λ < p(2 − p), hence

Typically, this value is close to one half of the invested capital w. In particular, the acceptance set of V@Rλ is not convex. This example also shows that V@R may strongly discourage diversification: It penalizes quite drastically the increase of the probability that something goes wrong, without rewarding the significant reduction of the expected loss conditional on the event of default. Thus, optimizing a portfolio with respect to V@Rλ may lead to a concentration of the portfolio in one single asset with a sufficiently small default probability, but with an exposure to large losses.

◊

Exercise 4.4.2. Let (Yn) be a sequence of independent and identically distributed random variables in L1(Ω,F, P). Show that

for any λ ∈ (0, 1). Then choose the common distribution in such a way that convexity is violated for large n, i.e.,

◊

In the remainder of this section, we will focus on monetary measures of risk which, in contrast to V@Rλ, are convex or even coherent on X := L∞. In particular, we are looking for convex risk measures which come close to V@Rλ. A first guess might be that one should take the smallest convex measure of risk, continuous from above, which dominates V@Rλ. However, since V@Rλ itself is not convex, the following proposition shows that such a smallest V@Rλ-dominating convex risk measure does not exist.

Proposition 4.47. For each X ∈ X and each λ ∈ (0, 1),

Proof. Let so that P[ X < q ]≤ λ. If A ∈ F satisfies P[ A ] > λ, then P[ A ∩ {X ≥ q} ] > 0. Thus, we may define a measure QA by

It follows that EQA[ −X ]≤ −q = V@Rλ(X).

Let Q := {QA | P[ A ] > λ}, and use this set to define a coherent risk measure ρ via

Then ρ(X) ≤ V@Rλ(X). Hence, the assertion will follow if we can show that ρ(Y) ≥ V@Rλ(Y) for each Y ∈ X . Let ε > 0 and A := {Y ≤ −V@Rλ(Y) + ε}. Clearly P[ A ] > λ, and so QA ∈ Q. Moreover, QA[ A ] = 1, and we obtain

Since ε > 0 is arbitrary, the result follows.

For the rest of this section, we concentrate on the following risk measure which is defined in terms of Value at Risk, but does satisfy the axioms of a coherent risk measure.

Definition 4.48. The Average Value at Risk at level λ ∈ (0, 1] of a position X ∈ X is given by

◊

Clearly, Average Value at Risk is a positively homogeneous monetary risk measure, since it inherits these properties from Value at Risk. Sometimes, the Average Value at Risk is also called the “Conditional Value at Risk” or the “Expected Shortfall”, and one writes CV@Rλ(X) or ESλ(X). These terms are motivated by formulas (4.47) and (4.45) below, but they are potentially misleading: “Conditional Value at Risk” might also be used to denote the Value at Risk with respect to a conditional distribution, and “Expected Shortfall” might be understood as the expectation of the shortfall X −. For these reasons, we prefer the term Average Value at Risk. Note that

by (4.44). In particular, the definition of AV@Rλ(X) makes sense for any X ∈ L1(Ω,F, P) and we have, in view of Lemma A.23,

Lemma A.23 also implies that, in the two preceding identities, can be replaced by any other quantile function of X.

Exercise 4.4.3. Recalling the results from Example 4.11 and Exercise 4.1.5, compute AV@Rλ(−X) when X is

(a) uniform,

(b) normally distributed,

(c) log-normally distributed, i.e., X = eσZ+μ with Z ∼ N(0, 1) and μ, σ ∈ ℝ,

(d) an indicator function, i.e., X = A for some event A ∈ F.

Then compare the behavior of V@Rλ(X) and AV@Rλ(X) as the parameter λ increases from 0 to 1.

◊

Remark 4.49. Theorem 2.57 shows that the partial order ≽uni of second-order stochastic dominance can be characterized in terms of Average Value at Risk:

where Xμ and Xν are random variables with distributions μ and ν that have finite mean.

◊

Remark 4.50. For X ∈ L∞, we have

Hence, it makes sense to define

which is the worst-case risk measure on L∞ introduced in Example 4.39. Recall that it is continuous from above but in general not from below.

◊

Proposition 4.51. For λ ∈ (0, 1) and any λ-quantile q of X,

Proof. Let qX be a quantile function with qX(λ) = q. By Lemma A.23,

This proves the first identity. The second one follows from Lemma A.26. It also follows from Exercise 4.4.1, since

due to the put-call parity (1.11).

Exercise 4.4.4. Use the representation (4.45) to show that AV@Rλ is subadditive.

◊

Since AV@Rλ is positively homogeneous, the preceding exercise, combined with Exercise 4.1.3, implies that AV@Rλ is a coherent risk measure. Alternatively, coherence is implied by the following representation (4.46).

Theorem 4.52. For λ ∈ (0, 1], AV@Rλ is a coherent risk measure which is continuous from below. It has the representation

where Qλ is the set of all probability measures Q P whose density dQ/dP is P-a.s. bounded by 1/λ. Moreover, Qλ is equal to the maximal set Qmax of Corollary 4.38.

Proof. Since Q1 = {P}, the assertion is obvious for λ = 1. For 0 < λ < 1, consider the coherent risk measure ρλ(X) := supQ∈Qλ EQ[ −X ]. First we assume that we are given some X < 0. We define a measure by d/dP = X/E[ X ]. Then

Clearly, the condition E[ φ ] = λ on the right can be replaced by E [ φ ] ≤ λ. Thus, we can apply the Neyman-Pearson lemma in the form of Theorem A.35 and conclude that the supremum is attained by

for a λ-quantile q of X and some κ ∈ [0, 1] for which E[ φ0 ] = λ. Hence,

Since dQ0 = λ−1φ0 dP defines a probability measure in Qλ, we conclude that

where we have used (4.45) in the last step. This proves (4.46) for X < 0. For arbitrary X ∈ L∞, we use the cash invariance of both ρλ and AV@Rλ. In particular, the representation (4.46) shows that AV@Rλ is a coherent risk measure.

It remains to prove that Qλ is the maximal set of Corollary 4.37. This follows from Exercise 4.3.4 and Example 4.40, but we also give a different argument here. To this end, we show that

for Q / ∈ Qλ. We denote by φ the density dQ/dP. There exist λʹ ∈ (0, λ) and k > 1/λʹ such that P[ φ ∧ k ≥ 1/λʹ ] > 0. For c > 0 define X(c) ∈ X by

Since

we have V@Rλ(X(c)) = 0, and (4.45) yields that

On the other hand,

Thus, the difference between EQ[ −X(c) ] and AV@Rλ(X(c)) becomes arbitrarily large as c ↑ ∞.

Finally, to show continuity from below, let q be a λ-quantile of X ∈ X . For any sequence (Xn) in X that increases to X, dominated convergence implies that

using the first identity in (4.45) in the first step and the second identity in (4.45) in the third step. Since AV@Rλ(X) ≤ AV@Rλ(Xn) by monotonicity, we have shown continuity from below.

Exercise 4.4.5. Use Corollary 4.38 and the Dunford–Pettis theorem (Theorem A.70) to give an alternative proof of the fact that AV@Rλ is continuous from below.

◊

Remark 4.53. The proof shows that for λ ∈ (0, 1) the maximum in (4.46) is attained by the measure Q0 ∈ Qλ, whose density is given by

where q is a λ-quantile of X, and where κ is defined as

◊

Corollary 4.54. For all X ∈ X ,

where WCEλ is the coherent risk measure defined in (4.41). Moreover, the first two inequalities are in fact identities if

which is the case if X has a continuous distribution.

Proof. If P[ A ]≥ λ, then the density of P[ ·| A ] with respect to P is bounded by 1 /λ. Therefore, Theorem 4.52 implies that AV@Rλ dominates WCEλ. Since

we have

and the second inequality follows by taking the limit ε ↓ 0. Moreover, (4.45) shows that

as soon as (4.48) holds.

Remark 4.55. We will see in Corollary 4.68 that the two coherent risk measuresAV@Rλ and WCEλ coincide if the underlying probability space is rich enough. If this is not the case, then the first inequality in (4.47) may be strict for some X; see [2]. Moreover, the functional

which is sometimes called the tail-conditional expectation of X, does not define a convex risk measure as will be shown in the following Exercise 4.4.6. Hence, the second inequality in (4.47) cannot reduce to an identity in general.

◊

Exercise 4.4.6. In this exercise we will show in particular that TCEλ, as defined in Remark 4.55, is typically not a coherent risk measure.

(a) Compute TCEλ(X) if X is the negative of an indicator function, i.e., X = −A for some event A ∈ F. Then compare the result with Exercise 4.4.3 (d) and Exercise 4.1.5 (c).

(b) Now let A, B ∈ F be two disjoint sets with probability p := P[ A ] = P[ B ] ∈ (0, 1/2). Show that for X := −A , Y := −B , and p ≤ λ < 2p,

◊

Remark 4.56. We have seen in Proposition 4.47 that there is no smallest convex risk measure dominating V@Rλ. But if we restrict our attention to the class of convex risk measures that dominate V@Rλ and only depend on the distribution of a random variable, then the situation is different. In fact, we will see in Theorem 4.67 that AV@Rλ is the smallest risk measure in this class, provided that the underlying probability space is rich enough. In this sense, Average Value at Risk can be regarded as the best conservative approximation to Value at Risk.

◊

4.5Law-invariant risk measures

Clearly, V@Rλ and AV@Rλ only involve the distribution of a position under the given probability measure P. In this section we study the class of all risk measures which share this property of law-invariance.

Definition 4.57. A monetary risk measure ρ on X = L∞(Ω,F, P) is called law-invariant if ρ(X) = ρ(Y) whenever X and Y have the same distribution under P.

◊

Throughout this section, we assume that the probability space (Ω,F, P) is rich enough in the sense that it supports a random variable with a continuous distribution. This condition is satisfied if and only if (Ω,F, P) is atomless; see Proposition A.31.

Remark 4.58. Any law-invariant monetary risk measure ρ is monotone with respect to the binary relation ≽mon of second-order stochastic dominance introduced in Definition 2.67. More precisely,

if X μ and X ν are random variables with distributions μ and ν. To prove this, let q μ and qν be quantile functions for μ and ν and take a random variable U with a uniform distribution on (0, 1). Then μ := qμ(U) ≥ qν(U) =: ν by Theorem 2.68, and μ and have the same distribution as X μ and Xν by Lemma A.23. Hence, law-invariance and monotonicity of ρ imply ρ(Xμ) = ρ(μ)≤ ρ(ν) = ρ(Xν).

◊

We can now formulate our first structure theorem for law-invariant convex risk measures.

Theorem 4.59. Let ρ be a convex risk measure and suppose that ρ is continuous from above. Then ρ is law-invariant if and only if its minimal penalty function αmin(Q) depends only on the law of under P when Q ∈ M1(P). In this case, ρ has the representation

and the minimal penalty function satisfies

For the proof, we will need the following lemma. Here and in the sequel we will write X ∼ to indicate that the two random variables X and have the same law.

Lemma 4.60. For two random variables X and Y,

provided that all occurring integrals are well-defined.

Proof. The upper Hardy–Littlewood inequality in Theorem A.28 yields “≥”. To prove the converse inequality, take a random variable U with a uniform distribution on (0, 1) such that Y = qY (U) P-a.s. Such a random variable U exists by Lemma A.32 and our assumption that the underlying probability space is atomless. Since := qX(U) ∼ X by Lemma A.23, we obtain

and hence “≤”.

Proof of Theorem 4.59. Suppose first that ρ is law-invariant. Then X ∈ Aρ implies that ∈ Aρ for all ∼ X. Hence,

where we have used Lemma 4.60 in the last step. It follows that αmin(Q) depends only on the law of φQ. We have thus also established the first identity in (4.50). For the second one, just note that := X +ρ(X) belongs to Aρ for any X ∈ L∞ and that q−X−ρ(X) is a quantile function for −.

Conversely, let us assume that αmin(Q) depends only on the law of φQ. For the moment, let us write ∼ Q to indicate that φQ and φ have the same law. Then Lemma 4.60 yields

We thus have established (4.49), and the law-invariance of ρ follows.

Exercise 4.5.1. For 0 < λ < 1, start from the definition of Average Value at Risk as

check that the conditions of Theorem 4.59 are satisfied, and deduce from (4.49) that the representation

holds.

◊

Example 4.61. Let u : ℝ → ℝ be an increasing concave function, and suppose that a position X ∈ L∞ is acceptable if E[ u(X) ]≥ c, where c is a given constant in the interior of u(ℝ). We have seen in Example 4.10 that the corresponding acceptance set induces a convex risk measure ρ. Clearly, ρ is law-invariant, and it will be shown in Proposition 4.113 that ρ is continuous from below and, hence, from above. Moreover, the corresponding minimal penalty function can be computed as

where

is the Fenchel–Legendre transform of the convex increasing loss function (x) := −u(−x); see Theorem 4.115.

◊

The following theorem clarifies the crucial role of the risk measures AV@Rλ: they can be viewed as the building blocks for law-invariant convex risk measures on L∞. Recall that we assume that (Ω,F, P) is atomless.

Theorem 4.62. A convex risk measure ρ is law-invariant and continuous from above if and only if

where

Proof. Clearly, the right-hand side of (4.51) defines a law-invariant convex risk measure that is continuous from above. Conversely, let ρ be law-invariant and continuous from above. We will show first that for Q ∈ M1(P) there exists a measure μ ∈ M1((0, 1]) such that

where Then the assertion will follow from Theorem 4.59. Since q−X(t) = V@R1−t(X) and qφ(t) = q+φ(t) for a.e. t ∈ (0, 1),

Since is increasing and right-continuous, we can write for some positive Radon measure ν on (0, 1]. Moreover, the measure μ given by μ(dt) = t ν(dt) is a probability measure on (0, 1]:

Thus,

Conversely, for any probability measure μ on (0, 1], the function q defined by q(t) := μ(ds) can be viewed as a quantile function of the density φ := q(U) of a measure Q ∈ M1(P), where U has a uniform distribution on (0, 1). Altogether, we obtain a one-to-one correspondence between laws of densities φ and probability measures μ on (0, 1].

Theorem 4.62 takes the following form for coherent risk measures.

Corollary 4.63. A coherent risk measure ρ is continuous from above and law-invariant if and only if

for some set M ⊂ M1((0, 1]).

Remark 4.64. In the preceding results of this section, it was assumed that ρ is law-invariant and continuous from above and that the underlying probability space is atomless. Under the additional regularity assumption that L2(Ω,F, P) is separable, it can be shown that every law-invariant convex risk measure is continuous from above; see [167].

◊

Randomness of a position is reduced in terms of P if we replace the position by its conditional expectation with respect to some σ-algebra G ⊂ F. Such a reduction of randomness is reflected by a convex risk measure if it is law-invariant:

Corollary 4.65. Assume that ρ is a convex risk measure which is continuous from above and law-invariant. Then ρ is monotone with respect to the binary relation ≽uni of second-order stochastic dominance introduced in (3.28):

for Y, X ∈ X . In particular,

for X ∈ X and any σ-algebra G ⊂ F, and

Proof. The first inequality follows from Theorem 4.62 combined with Remark 4.49. The second inequality is a special case of the first one, since E [ X |G ] ≽uni X according to Theorem 2.57. The third follows from the second by taking G = {∅, Ω}.

Recall from Theorem 2.68 that μ ≽mon ν implies μ ≽uni ν. Thus, the preceding conclusion for convex risk measures is stronger than the one of Remark 4.58 for monetary risk measures.

Remark 4.66. If G1 ⊂ G2 ⊂ · · · ⊂ F are σ-algebras, then

where ρ is as in Corollary 4.65 and Indeed, Doob’s martingale convergence theorem (see, e.g., Theorem 19.1 in [20]) states that E[ X | Gn ] → E[ X | G∞ ] P-a.s. as n ↑ ∞. Hence, the Fatou property and Corollary 4.65 show that

◊

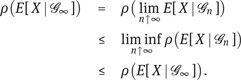
In contrast to Proposition 4.47, the following theorem shows that AV@Rλ is the best conservative approximation to V@Rλ in the class of all law-invariant convex risk measures which are continuous from above.

Theorem 4.67. AV@Rλ is the smallest law-invariant convex measure of risk that is continuous from above and dominates V@Rλ.

Proof. That AV@Rλ dominates V@Rλ was already stated in (4.47). Suppose now that ρ is another law-invariant convex risk measure which dominates V@Rλ and which is continuous from above. We must show that for a given X ∈ X

By cash invariance, we may assume without loss of generality that X > 0. Take ε > 0, and let A := {−X ≥ V@Rλ(X) − ε} and

Since on Ac, we get P[ Y < E[ X | A ] ] = 0. On the other hand, P[ Y ≤ E[ X | A ]]≥ P[ A ] > λ, and this implies that V@Rλ(Y) = E[ −X | A ]. Since ρ dominates V@Rλ, we have ρ(Y) ≥ E[ −X | A ]. Thus,

by Corollary 4.65. Taking ε ↓ 0 yields

If the distribution of X is continuous, Corollary 4.54 states that the conditional expectation on the right equals AV@Rλ(X), and we obtain (4.53). If the distribution of X is not continuous, we denote by D the set of all points x such that P[ X = x ] > 0 and take any bounded random variable Z ≥ 0 with a continuous distribution. Such a random variable exists due to our assumption that (Ω,F, P) is atomless. Note that has a continuous distribution. Indeed, for any x,

Moreover, X n decreases to X. The inequality (4.53) holds for each X n and extends to X by continuity from above.

Corollary 4.68. AV@Rλ and WCEλ coincide under our assumption that the probability space is atomless.

Proof. We know from Corollary 4.54 that WCEλ(X) = AV@Rλ(X) if X has a continuous distribution. Repeating the approximation argument at the end of the preceding proof yields WCEλ(X) = AV@Rλ(X) for each X ∈ X .