Information theory originated in the late 1940s from the seminal papers by Claude Shannon. One of the primary motivations behind Shannon’s mathematical theory of information was the problem of finding a more compact way of representing data. In short, he was concerned with the problem of compression. In this section we briefly touch on the relationship between entropy and compression and introduce Huffman codes as a method for more succinctly representing data.

For more on how to compress data, see [Cover-Thomas] or [Nelson-Gailly].

Example

Suppose we have an alphabet with four letters $a\text{,}b\text{,}c\text{,}d$, and suppose these letters appear in a text with frequencies as follows.

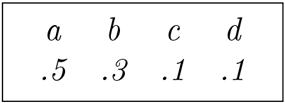
We could represent $a$ as the binary string 00, $b$ as 01, $c$ as 10, and $d$ as 11. This means that the message would average two bits per letter. However, suppose we represent $a$ as 1, $b$ as 01, $c$ as 001, and $d$ as 000. Then the average number of bits per letter is

$$(1)(.5)+(2)(.3)+(3)(.1)+(3)(.1)=1.7$$

(the number of bits for $a$ times the frequency of $a$, plus the number of bits for $b$ times the frequency of $b$, etc.). This encoding of the letters is therefore more efficient.

In general, we have a random variable with outputs in a set $\mathit{X}$. We want to represent the outputs in binary in an efficient way; namely, the average number of bits per output should be as small as possible.

An early example of such a procedure is Morse code, which represents letters as sequences of dots and dashes and was developed to send messages by telegraph. Morse asked printers which letters were used most, and made the more frequent letters have smaller representations. For example, $e$ is represented as $\cdot$ and $t$ as $-$. But $x$ is $-\cdot \cdot -$ and $z$ is $--\cdot \cdot$.

A more recent method was developed by Huffman. The idea is to list all the outputs and their probabilities. The smallest two are assigned 1 and 0 and then combined to form an output with a larger probability. The same procedure is then applied to the new list, assigning 1 and 0 to the two smallest, then combining them to form a new list. This procedure is continued until there is only one output remaining. The binary strings are then obtained by reading backward through the procedure, recording the bits that have been assigned to a given output and to combinations containing it. This is best explained by an example.

Suppose we have outputs $a\text{,}b\text{,}c\text{,}d$ with probabilities $0.5\text{,}0.3\text{,}0.1\text{,}0.1$, as in the preceding example. The diagram in Figure 20.1 gives the procedure.

Figure 20.1 An Example of Huffman Encoding

Note that when there were two choices for the lowest, we made a random choice for which one received 0 and which one received 1. Tracing backward through the table, we see that $a$ only received a 1, $b$ received 01, $c$ received 001, and $d$ received 000. These are exactly the assignments made previously that gave a low number of bits per letter.

A useful feature of Huffman encoding is that it is possible to read a message one letter at a time. For example, the string 011000 can only be read as $bad$; moreover, as soon as we have read the first two bits 01, we know that the first letter is $b$.

Suppose instead that we wrote the bits assigned to letters in reverse order, so $b$ is 10 and $c$ is 001. Then the message 101000 cannot be determined until all bits have been read, since it potentially could start with $bb$ or $ba$.

Even worse, suppose we had assigned 0 to $a$ instead of 1. Then the messages $aaa$ and $d$ would be the same. It is possible to show that Huffman encoding avoids these two problems.

The average number of bits per output is closely related to the entropy.

This result agrees with the interpretation that the entropy measures how many bits of information are contained in the output of $X$. We omit the proof. In our example, the entropy is