In the RSA algorithm, we saw how the difficulty of factoring yields useful cryptosystems. There is another number theory problem, namely discrete logarithms, that has similar applications.

Fix a prime $p$. Let $\alpha$ and $\beta$ be nonzero integers mod $p$ and suppose

The problem of finding $x$ is called the discrete logarithm problem. If $n$ is the smallest positive integer such that $\begin{array}{cc}{\alpha }^n\equiv 1& (\text{mod}p)\end{array}$, we may assume $0\le x<n$, and then we denote

and call it the discrete log of $\beta$ with respect to $\alpha$ (the prime $p$ is omitted from the notation).

For example, let $p=11$ and let $\alpha =2$. Since $2^6\equiv 9(\text{mod}11)$, we have $L_2(9)=6$. Of course, $2^6\equiv 2^{16}\equiv 2^{26}\equiv 9(\text{mod}11)$, so we could consider taking any one of 6, 16, 26 as the discrete logarithm. But we fix the value by taking the smallest nonnegative value, namely 6. Note that we could have defined the discrete logarithm in this case to be the congruence class 6 mod 10. In some ways, this would be more natural, but there are applications where it is convenient to have a number, not just a congruence class.

Often, $\alpha$ is taken to be a primitive root mod $p$, which means that every $\beta$ is a power of $\alpha (\text{mod}p)$. If $\alpha$ is not a primitive root, then the discrete logarithm will not be defined for certain values of $\beta$.

Given a prime $p$, it is fairly easy to find a primitive root in many cases. See Exercise 54 in Chapter 3.

The discrete log behaves in many ways like the usual logarithm. In particular, if $\alpha$ is a primitive root mod $p$, then

(see Exercise 6).

When $p$ is small, it is easy to compute discrete logs by exhaustive search through all possible exponents. However, when $p$ is large this is not feasible. We give some ways of attacking discrete log problems later. However, it is believed that discrete logs are hard to compute in general. This assumption is the basis of several cryptosystems.

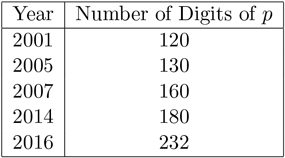
The size of the largest primes for which discrete logs can be computed has usually been approximately the same size as the size of largest integers that could be factored (both of these refer to computations that would work for arbitrary numbers of these sizes; special choices of integers will succumb to special techniques, and thus discrete log computations and factorizations work for much larger specially chosen numbers). Compare Table 10.1 with Table 9.2 in Chapter 9.

Table 10.1 Discrete Log Records

A function $f(x)$ is called a one-way function if $f(x)$ is easy to compute, but, given $y$, it is computationally infeasible to find $x$ with $f(x)=y$. Modular exponentiation is probably an example of such a function. It is easy to compute ${\alpha }^x(\text{mod}p)$, but solving ${\alpha }^x\equiv \beta$ for $x$ is probably hard. Multiplication of large primes can also be regarded as a (probable) one-way function: It is easy to multiply primes but difficult to factor the result to recover the primes. One-way functions have many cryptographic uses.