An elliptic curve $E$ is the graph of an equation

where $a\text{,}b\text{,}c$ are in whatever is the appropriate set (rational numbers, real numbers, integers mod $p\text{,}$ etc.). In other words, let $K$ be the rational numbers, the real numbers, or the integers mod a prime $p$ (or, for those who know what this means, any field of characteristic not 2; but see Section 21.4). Then we assume $a\text{,}b\text{,}c\in K$ and take $E$ to be

As will be discussed below, it is also convenient to include a point $(\text{∞}\text{,}\text{∞})\text{,}$ which often will be denoted simply by $\text{∞}\text{.}$

Let’s consider the case of real numbers first, since this case allows us to work with pictures. The graph $E$ has two possible forms, depending on whether the cubic polynomial has one real root or three real roots. For example, the graphs of $y^2=x(x+1)(x-1)$ and $y^2=x^3+73$ are the following:

21.1-1 Full Alternative Text

21.1-2 Full Alternative Text

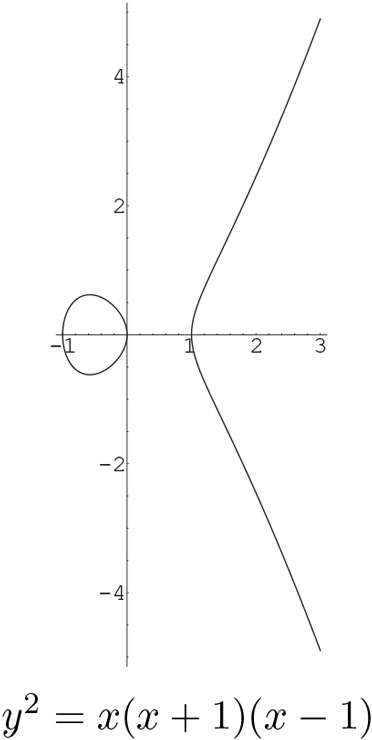
The case of two components (for example, $y^2=x(x+1)(x-1)$) occurs when the cubic polynomial has three real roots. The case of one component (for example, $y^2=x^3+73$) occurs when the cubic polynomial has only one real root.

For technical reasons that will become clear later, we also include a “point at infinity,” denoted $\text{∞}\text{,}$ which is most easily regarded as sitting at the top of the $y\text{-axis}$. It can be treated rigorously in the context of projective geometry (see [Washington]), but this intuitive notion suffices for what we need. The bottom of the $y\text{-axis}$ is identified with the top, so $\text{∞}$ also sits at the bottom of the $y\text{-axis}$.

Now let’s look at elliptic curves mod $p\text{,}$ where $p$ is a prime. For example, let $E$ be given by

We can list the points on $E$ by letting $x$ run through the values $0\text{,}1\text{,}2\text{,}3\text{,}4$ and solving for $y\text{:}$

Note that we again include a point $\text{∞}\text{.}$

Elliptic curves mod $p$ are finite sets of points. It is these elliptic curves that are useful in cryptography.

Technical point: We assume that the cubic polynomial $x^3+a{x}^2+bx+c$ has no multiple roots. This means we exclude, for example, the graph of $y^2=(x-1{)}^2(x+2)\text{.}$ Such curves will be discussed in Subsection 21.3.1.

Technical point: For most situations, equations of the form $y^2=x^3+bx+c$ suffice for elliptic curves. In fact, in situations where we can divide by 3, a change of variables changes an equation $y^2=x^3+a{x}^2+bx+c$ into an equation of the form $y^2=x^3+b^{\prime }x+c^{\prime }\text{.}$ See Exercise 1. However, sometimes it is necessary to consider elliptic curves given by equations of the form

where $a_1\text{,}\dots \text{,}{a}_6$ are constants. If we are working mod $p\text{,}$ where $p>3$ is prime, or if we are working with real, rational, or complex numbers, then simple changes of variables transform the present equation into the form $y^2=x^3+bx+c\text{.}$ However, if we are working mod 2 or mod 3, or with a finite field of characteristic 2 or 3 (that is, $1+1=0$ or $1+1+1=0$), then we need to use the more general form. Elliptic curves over fields of characteristic 2 will be mentioned briefly in Section 21.4.

Historical point: Elliptic curves are not ellipses. They received their name from their relation to elliptic integrals such as

that arise in the computation of the arc length of ellipses.

The main reason elliptic curves are important is that we can use any two points on the curve to produce a third point on the curve. Given points $P_1$ and $P_2$ on $E\text{,}$ we obtain a third point $P_3$ on $E$ as follows (see Figure 21.1): Draw the line $L$ through $P_1$ and $P_2$ (if $P_1=P_2\text{,}$ take the tangent line to $E$ at $P_1$). The line $L$ intersects $E$ in a third point $Q\text{.}$ Reflect $Q$ through the $x\text{-axis}$ (i.e., change $y$ to $-y$) to get $P_3\text{.}$ Define a law of addition on $E$ by

Figure 21.1 Adding Points on an Elliptic Curve

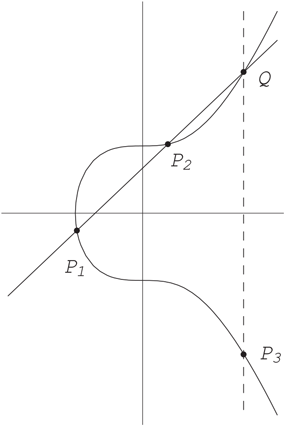
Note that this is not the same as adding points in the plane.

What happens if we try to compute $P+\text{∞}$? We make the convention that the lines through $\text{∞}$ are vertical. Therefore, the line through $P=(x\text{,}y)$ and $\text{∞}$ intersects $E$ in $P$ and also in $(x\text{,}-y)\text{.}$ When we reflect $(x\text{,}-y)$ across the $x\text{-axis}$, we get back $P=(x\text{,}y)\text{.}$ Therefore,

We can also subtract points. First, observe that the line through $(x\text{,}y)$ and $(x\text{,}-y)$ is vertical, so the third point of intersection with $E$ is $\text{∞}\text{.}$ The reflection across the $x\text{-axis}$ is still $\text{∞}$ (that’s what we meant when we said $\text{∞}$ sits at the top and at the bottom of the $y\text{-axis}$). Therefore,

Since $\text{∞}$ plays the role of an additive identity (in the same way that 0 is the identity for addition with integers), we define

To subtract points $P-Q\text{,}$ simply add $P$ and $-Q\text{.}$

Another way to express the addition law is to say that

(See Exercise 17.)

For computations, we can ignore the geometrical interpretation and work only with formulas, which are as follows:

It can be shown that the addition law is associative:

It is also commutative:

When adding several points, it therefore doesn’t matter in what order the points are added nor how they are grouped together. In technical terms, we have found that the points of $E$ form an abelian group. The point $\text{∞}$ is the identity element of this group.

If $k$ is a positive integer and $P$ is a point on an elliptic curve, we can define

We can extend this to negative $k\text{.}$ For example, $(-3)P=3(-P)=(-P)+(-P)+(-P)\text{,}$ where $-P$ is the reflection of $P$ across the $x\text{-axis}$. The associative law means that we can group the summands in any way we choose when computing a multiple of a point. For example, suppose we want to compute $100P\text{.}$ We do the additive version of successive squaring that was used in modular exponentiation:

The associative law means, for example, that $4P$ can be computed as $2P+2P=(P+P)+(P+P)\text{.}$ It also could have been computed in what might seem to be a more natural way as $((P+P)+P)+P\text{,}$ but this is slower because it requires three additions instead of two.

For more examples, see Examples 41–44 in the Computer Appendices.