We eventually want to describe how to attack the above system when it uses four rounds, but we need to start by analyzing three rounds. Therefore, we temporarily start with $L_1{R}_1$ instead of $L_0{R}_0$.

The situation is now as follows. We have obtained access to a three-round encryption device that uses the preceding procedure. We know all the inner workings of the encryption algorithm such as the S-boxes, but we do not know the key. We want to find the key by a chosen plaintext attack. We use various inputs $L_1{R}_1$ and obtain outputs $L_4{R}_4$.

We have

Suppose we have another message $L_1^{\ast }{R}_1^{\ast }$ with $R_1=R_1^{\ast }$. For each $i$, let ${R_i}^{\prime }=R_i\oplus R_i^{\ast }$ and ${L_i}^{\prime }=L_i\oplus L_i^{\ast }$. Then ${L_i}^{\prime }{R_i}^{\prime }$ is the “difference” (or sum; we are working mod 2) of $L_i{R}_i$ and $L_i^{\ast }{R}_i^{\ast }$. The preceding calculation applied to $L_1^{\ast }{R}_1^{\ast }$ yields a formula for $R_4^{\ast }$. Since we have assumed that $R_1=R_1^{\ast }$, we have $f(R_1\text{,}{K}_2)=f(R_1^{\ast }\text{,}{K}_2)$. Therefore, $f(R_1\text{,}{K}_2)\oplus f(R_1^{\ast }\text{,}{K}_2)=0$ and

This may be rearranged to

Finally, since $R_3=L_4$ and $R_3^{\ast }=L_4^{\ast }$, we obtain

Note that if we know the input XOR, namely ${L_1}^{\prime }{R_1}^{\prime }$, and if we know the outputs $L_4{R}_4$ and $L_4^{\ast }{R}_4^{\ast }$, then we know everything in this last equation except $K_4$.

Now let’s analyze the inputs to the S-boxes used to calculate $f(L_4\text{,}{K}_4)$ and $f(L_4^{\ast }\text{,}{K}_4)$. If we start with $L_4$, we first expand and then XOR with $K_4$ to obtain $E(L_4)\oplus K_4$, which are the bits sent to $S_1$ and $S_2$. Similarly, $L_4^{\ast }$ yields $E(L_4^{\ast })\oplus K_4$. The XOR of these is

(the first equality follows easily from the bit-by-bit description of the expansion function). Therefore, we know

1. the XORs of the inputs to the two S-boxes (namely, the first four and the last four bits of $E(L_4^{{}^{\prime }})$);

2. the XORs of the two outputs (namely, the first three and the last three bits of $R_4^{{}^{\prime }}\oplus L_1^{{}^{\prime }}$).

Let’s restrict our attention to $S_1$. The analysis for $S_2$ will be similar. It is fairly fast to run through all pairs of four-bit inputs with a given XOR (there are only 16 of them) and see which ones give a desired output XOR. These can be computed once for all and stored in a table.

For example, suppose we have input XOR equal to 1011 and we are looking for output XOR equal to 100. We can run through the input pairs (1011, 0000), (1010, 0001), (1001, 0010), ..., each of which has XOR equal to 1011, and look at the output XORs. We find that the pairs (1010, 0001) and (0001, 1010) both produce output XORs 100. For example, 1010 means we look at the second row, third column of $S_1$, which is 110. Moreover, 0001 means we look at the first row, second column, which is 010. The output XOR is therefore $110\oplus 010=100$.

We know $L_4$ and $L_4^{\ast }$. For example, suppose $L_4=101110$ and $L_4^{\ast }=000010$. Therefore, $E(L_4)=10111110$ and $E(L_4^{\ast })=00000010$, so the inputs to $S_1$ are $1011\oplus K_4^L$ and $0000\oplus K_4^L$, where $K_4^L$ denotes the left four bits of $K_4$. If we know that the output XOR for $S_1$ is 100, then $(1011\oplus K_4^L\text{,}0000\oplus K_4^L)$ must be one of the pairs on the list we just calculated, namely (1010, 0001) and (0001, 1010). This means that $K_4^L=0001$ or 1010.

If we repeat this procedure a few more times, we should be able to eliminate one of the two choices for $K_4$ and hence determine four bits of $K$. Similarly, using $S_2$, we find four more bits of $K$. We therefore know eight of the nine bits of $K$. The last bit can be found by trying both possibilities and seeing which one produces the same encryptions as the machine we are attacking.

Here is a summary of the procedure (for notational convenience, we describe it with both S-boxes used simultaneously, though in the examples we work with the S-boxes separately):

1. Look at the list of pairs with input $\text{XOR}=E(L_4^{{}^{\prime }})$ and output $\text{XOR}=R_4^{{}^{\prime }}\oplus L_1^{{}^{\prime }}$.

2. The pair $(E(L_4)\oplus K_4\text{,}E(L_4^{\ast })\oplus K_4)$ is on this list.

3. Deduce the possibilities for $K_4$.

4. Repeat until only one possibility for $K_4$ remains.

Suppose now that we have obtained access to a four-round device. Again, we know all the inner workings of the algorithm except the key, and we want to determine the key. The analysis we used for three rounds still applies, but to extend it to four rounds we need to use more probabilistic techniques.

There is a weakness in the box $S_1$. If we look at the 16 input pairs with XOR equal to 0011, we discover that 12 of them have output XOR equal to 011. Of course, we expect on the average that two pairs should yield a given output XOR, so the present case is rather extreme. A little variation is to be expected; we’ll see that this large variation makes it easy to find the key.

There is a similar weakness in $S_2$, though not quite as extreme. Among the 16 input pairs with XOR equal to 1100, there are eight with output XOR equal to 010.

Suppose now that we start with randomly chosen $R_0$ and $R_0^{\ast }$ such that $R_0^{\prime }=R_0\oplus R_0^{\ast }=001100$. This is expanded to $E(001100)=00111100$. Therefore the input XOR for $S_1$ is 0011 and the input XOR for $S_2$ is 1100. With probability 12/16 the output XOR for $S_1$ will be 011, and with probability 8/16 the output XOR for $S_2$ will be 010. If we assume the outputs of the two S-boxes are independent, we see that the combined output XOR will be 011010 with probability (12/16)(8/16) = 3/8. Because the expansion function sends bits 3 and 4 to both $S_1$ and $S_2$, the two boxes cannot be assumed to have independent outputs, but 3/8 should still be a reasonable estimate for what happens.

Now suppose we choose $L_0$ and $L_0^{\ast }$ so that ${L_0}^{\prime }=L_0\oplus L_0^{\ast }=011010$. Recall that in the encryption algorithm the output of the S-boxes is XORed with $L_0$ to obtain $R_1$. Suppose the output XOR of the S-boxes is 011010. Then ${R_1}^{\prime }=011010\oplus {L_0}^{\prime }=000000$. Since ${R_1}^{\prime }=R_1\oplus R_1^{\ast }$, it follows that $R_1=R_1^{*}\text{.}$

Putting everything together, we see that if we start with two randomly chosen messages with XOR equal to $L_0^{{}^{\prime }}{R}_0^{{}^{\prime }}=011010001100$, then there is a probability of around 3/8 that ${L_1}^{\prime }{R_1}^{\prime }=001100000000$.

Here’s the strategy for finding the key. Try several randomly chosen pairs of inputs with XOR equal to 011010001100. Look at the outputs $L_4{R}_4$ and $L_4^{\ast }{R}_4^{\ast }$. Assume that $L_1^{{}^{\prime }}{R}_1^{{}^{\prime }}=001100000000$. Then use three-round differential cryptanalysis with $L_1^{{}^{\prime }}=001100$ and the known outputs to deduce a set of possible keys $K_4$. When $L_1^{{}^{\prime }}{R}_1^{{}^{\prime }}=001100000000$, which should happen around 3/8 of the time, this list of keys will contain $K_4$, along with some other random keys. The remaining 5/8 of the time, the list should contain random keys. Since there seems to be no reason that any incorrect key should appear frequently, the correct key $K_4$ will probably appear in the lists of keys more often than the other keys.

Here is an example. Suppose we are attacking a four-round device. We try one hundred random pairs of inputs $L_0{R}_0$ and $L_0^{\ast }{R}_0^{\ast }=L_0{R}_0\oplus 011010001100$. The frequencies of possible keys we obtain are in the following table. We find it easier to look at the first four bits and the last four bits of $K_4$ separately.

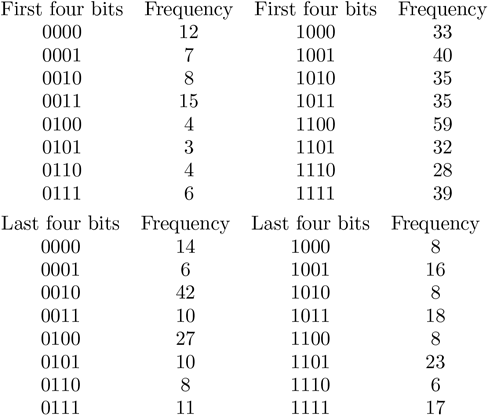
It is therefore likely that $K_4=11000010$. Therefore, the key $K$ is 10*110000.

To determine the remaining bit, we proceed as before. We can compute that 000000000000 is encrypted to 100011001011 using $K=101110000$ and is encrypted to 001011011010 using $K=100110000$. If the machine we are attacking encrypts 000000000000 to 100011001011, we conclude that the second key cannot be correct, so the correct key is probably $K=101110000$.

The preceding attack can be extended to more rounds by extensions of these methods. It might be noticed that we could have obtained the key at least as quickly by simply running through all possibilities for the key. That is certainly true in this simple model. However, in more elaborate systems such as DES, differential cryptanalytic techniques are much more efficient than exhaustive searching through all keys, at least until the number of rounds becomes fairly large. In particular, the reason that DES uses 16 rounds appears to be because differential cryptanalysis is more efficient than exhaustive search until 16 rounds are used.

There is another attack on DES, called linear cryptanalysis, that was developed by Mitsuru Matsui [Matsui]. The main ingredient is an approximation of DES by a linear function of the input bits. It is theoretically faster than an exhaustive search for the key and requires around $2^{43}$ plaintext–ciphertext pairs to find the key. It seems that the designers of DES had not anticipated linear cryptanalysis. For details of the method, see [Matsui].