1.1 Secure Communications
In the basic communication scenario, depicted in Figure 1.1, there are two parties, we’ll call them Alice and Bob, who want to communicate with each other. A third party, Eve, is a potential eavesdropper.
Figure 1.1 The Basic Communication Scenario for Cryptography.
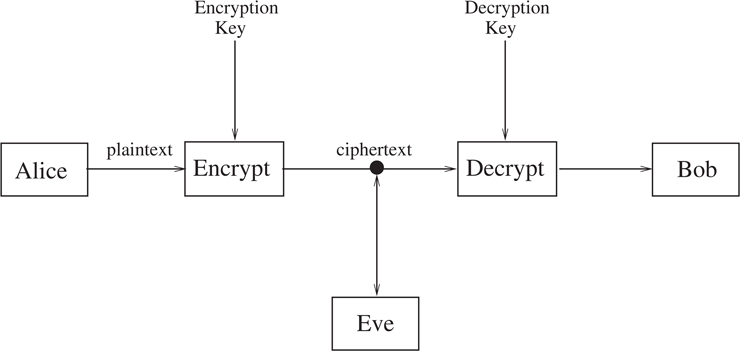
When Alice wants to send a message, called the plaintext, to Bob, she encrypts it using a method prearranged with Bob. Usually, the encryption method is assumed to be known to Eve; what keeps the message secret is a key. When Bob receives the encrypted message, called the ciphertext, he changes it back to the plaintext using a decryption key.
Eve could have one of the following goals:
Read the message.
Find the key and thus read all messages encrypted with that key.
Corrupt Alice’s message into another message in such a way that Bob will think Alice sent the altered message.
Masquerade as Alice, and thus communicate with Bob even though Bob believes he is communicating with Alice.
Which case we’re in depends on how evil Eve is. Cases (3) and (4) relate to issues of integrity and authentication, respectively. We’ll discuss these shortly. A more active and malicious adversary, corresponding to cases (3) and (4), is sometimes called Mallory in the literature. More passive observers (as in cases (1) and (2)) are sometimes named Oscar. We’ll generally use only Eve, and assume she is as bad as the situation allows.
1.1.1 Possible Attacks
There are four main types of attack that Eve might be able to use. The differences among these types of attacks are the amounts of information Eve has available to her when trying to determine the key. The four attacks are as follows:
Ciphertext only: Eve has only a copy of the ciphertext.
Known plaintext: Eve has a copy of a ciphertext and the corresponding plaintext. For example, suppose Eve intercepts an encrypted press release, then sees the decrypted release the next day. If she can deduce the decryption key, and if Alice doesn’t change the key, Eve can read all future messages. Or, if Alice always starts her messages with “Dear Bob,” then Eve has a small piece of ciphertext and corresponding plaintext. For many weak cryptosystems, this suffices to find the key. Even for stronger systems such as the German Enigma machine used in World War II, this amount of information has been useful.
Chosen plaintext: Eve gains temporary access to the encryption machine. She cannot open it to find the key; however, she can encrypt a large number of suitably chosen plaintexts and try to use the resulting ciphertexts to deduce the key.
Chosen ciphertext: Eve obtains temporary access to the decryption machine, uses it to “decrypt” several strings of symbols, and tries to use the results to deduce the key.
A chosen plaintext attack could happen as follows. You want to identify an airplane as friend or foe. Send a random message to the plane, which encrypts the message automatically and sends it back. Only a friendly airplane is assumed to have the correct key. Compare the message from the plane with the correctly encrypted message. If they match, the plane is friendly. If not, it’s the enemy. However, the enemy can send a large number of chosen messages to one of your planes and look at the resulting ciphertexts. If this allows them to deduce the key, the enemy can equip their planes so they can masquerade as friendly.
An example of a known plaintext attack reportedly happened in World War II in the Sahara Desert. An isolated German outpost every day sent an identical message saying that there was nothing new to report, but of course it was encrypted with the key being used that day. So each day the Allies had a plaintext-ciphertext pair that was extremely useful in determining the key. In fact, during the Sahara campaign, General Montgomery was carefully directed around the outpost so that the transmissions would not be stopped.
One of the most important assumptions in modern cryptography is Kerckhoffs’s principle: In assessing the security of a cryptosystem, one should always assume the enemy knows the method being used. This principle was enunciated by Auguste Kerckhoffs in 1883 in his classic treatise La Cryptographie Militaire. The enemy can obtain this information in many ways. For example, encryption/decryption machines can be captured and analyzed. Or people can defect or be captured. The security of the system should therefore be based on the key and not on the obscurity of the algorithm used. Consequently, we always assume that Eve has knowledge of the algorithm that is used to perform encryption.
1.1.2 Symmetric and Public Key Algorithms
Encryption/decryption methods fall into two categories: symmetric key and public key. In symmetric key algorithms, the encryption and decryption keys are known to both Alice and Bob. For example, the encryption key is shared and the decryption key is easily calculated from it. In many cases, the encryption key and the decryption key are the same. All of the classical (pre-1970) cryptosystems are symmetric, as are the more recent Data Encryption Standard (DES) and Advanced Encryption Standard (AES).
Public key algorithms were introduced in the 1970s and revolutionized cryptography. Suppose Alice wants to communicate securely with Bob, but they are hundreds of kilometers apart and have not agreed on a key to use. It seems almost impossible for them to do this without first getting together to agree on a key, or using a trusted courier to carry the key from one to the other. Certainly Alice cannot send a message over open channels to tell Bob the key, and then send the ciphertext encrypted with this key. The amazing fact is that this problem has a solution, called public key cryptography. The encryption key is made public, but it is computationally infeasible to find the decryption key without information known only to Bob. The most popular implementation is RSA (see Chapter 9), which is based on the difficulty of factoring large integers. Other versions (see Chapters 10, 23, and 24) are the ElGamal system (based on the discrete log problem), NTRU (lattice based) and the McEliece system (based on error correcting codes).
Here is a nonmathematical way to do public key communication. Bob sends Alice a box and an unlocked padlock. Alice puts her message in the box, locks Bob’s lock on it, and sends the box back to Bob. Of course, only Bob can open the box and read the message. The public key methods mentioned previously are mathematical realizations of this idea. Clearly there are questions of authentication that must be dealt with. For example, Eve could intercept the first transmission and substitute her own lock. If she then intercepts the locked box when Alice sends it back to Bob, Eve can unlock her lock and read Alice’s message. This is a general problem that must be addressed with any such system.
Public key cryptography represents what is possibly the final step in an interesting historical progression. In the earliest years of cryptography, security depended on keeping the encryption method secret. Later, the method was assumed known, and the security depended on keeping the (symmetric) key private or unknown to adversaries. In public key cryptography, the method and the encryption key are made public, and everyone knows what must be done to find the decryption key. The security rests on the fact (or hope) that this is computationally infeasible. It’s rather paradoxical that an increase in the power of cryptographic algorithms over the years has corresponded to an increase in the amount of information given to an adversary about such algorithms.
Public key methods are very powerful, and it might seem that they make the use of symmetric key cryptography obsolete. However, this added flexibility is not free and comes at a computational cost. The amount of computation needed in public key algorithms is typically several orders of magnitude more than the amount of computation needed in algorithms such as DES or AES/Rijndael. The rule of thumb is that public key methods should not be used for encrypting large quantities of data. For this reason, public key methods are used in applications where only small amounts of data must be processed (for example, digital signatures and sending keys to be used in symmetric key algorithms).
Within symmetric key cryptography, there are two types of ciphers: stream ciphers and block ciphers. In stream ciphers, the data are fed into the algorithm in small pieces (bits or characters), and the output is produced in corresponding small pieces. We discuss stream ciphers in Chapter 5. In block ciphers, however, a block of input bits is collected and fed into the algorithm all at once, and the output is a block of bits. Mostly we shall be concerned with block ciphers. In particular, we cover two very significant examples. The first is DES, and the second is AES, which was selected in the year 2000 by the National Institute for Standards and Technology as the replacement for DES. Public key methods such as RSA can also be regarded as block ciphers.
Finally, we mention a historical distinction between different types of encryption, namely codes and ciphers. In a code, words or certain letter combinations are replaced by codewords (which may be strings of symbols). For example, the British navy in World War I used 03680C, 36276C, and 50302C to represent shipped at, shipped by, and shipped from, respectively. Codes have the disadvantage that unanticipated words cannot be used. A cipher, on the other hand, does not use the linguistic structure of the message but rather encrypts every string of characters, meaningful or not, by some algorithm. A cipher is therefore more versatile than a code. In the early days of cryptography, codes were commonly used, sometimes in conjunction with ciphers. They are still used today; covert operations are often given code names. However, any secret that is to remain secure needs to be encrypted with a cipher. In this book, we’ll deal exclusively with ciphers.
1.1.3 Key Length
The security of cryptographic algorithms is a difficult property to measure. Most algorithms employ keys, and the security of the algorithm is related to how difficult it is for an adversary to determine the key. The most obvious approach is to try every possible key and see which ones yield meaningful decryptions. Such an attack is called a brute force attack. In a brute force attack, the length of the key is directly related to how long it will take to search the entire keyspace. For example, if a key is long, then there are The DES algorithm has a and thus has
In many situations we’ll encounter in this book, it will seem that a system can be broken by simply trying all possible keys. However, this is often easier said than done. Suppose you need to try possibilities and you have a computer that can do such calculations each second. There are around in a year, so it would take a little more than to complete the task, longer than the predicted life of the universe.
Longer keys are advantageous but are not guaranteed to make an adversary’s task difficult. The algorithm itself also plays a critical role. Some algorithms might be able to be attacked by means other than brute force, and some algorithms just don’t make very efficient use of their keys’ bits. This is a very important point to keep in mind. Not all algorithms are created equal!
For example, one of the easiest cryptosystems to break is the substitution cipher, which we discuss in Section 2.4. The number of possible keys is . In contrast, DES (see Chapter 7) has only But it typically takes over a day on a specially designed computer to find a DES key. The difference is that an attack on a substitution cipher uses the underlying structure of the language, while the attack on DES is by brute force, trying all possible keys.
A brute force attack should be the last resort. A cryptanalyst always hopes to find an attack that is faster. Examples we’ll meet are frequency analysis (for the substitution and Vigenère ciphers) and birthday attacks (for discrete logs).
We also warn the reader that just because an algorithm seems secure now, we can’t assume that it will remain so. Human ingenuity has led to creative attacks on cryptographic protocols. There are many examples in modern cryptography where an algorithm or protocol was successfully attacked because of a loophole presented by poor implementation, or just because of advances in technology. The DES algorithm, which withstood years of cryptographic scrutiny, ultimately succumbed to attacks by a well-designed parallel computer. Even as you read this book, research in quantum computing is underway, which could dramatically alter the terrain of future cryptographic algorithms.
For example, the security of several systems we’ll study depends on the difficulty of factoring large integers, say of around 600 digits. Suppose you want to factor a number of this size. The method used in elementary school is to divide by all of the primes up to the square root of . There are approximately less than . Trying each one is impossible. The number of electrons in the universe is estimated to be less than . Long before you finish your calculation, you’ll get a call from the electric company asking you to stop. Clearly, more sophisticated factoring algorithms must be used, rather than this brute force type of attack. When RSA was invented, there were some good factoring algorithms available, but it was predicted that a 129-digit number such as the RSA challenge number (see Chapter 9) would not be factored within the foreseeable future. However, advances in algorithms and computer architecture have made such factorizations fairly routine (although they still require substantial computing resources), so now numbers of several hundred digits are recommended for security. But if a full-scale quantum computer is ever built, factorizations of even these numbers will be easy, and the whole RSA scheme (along with many other methods) will need to be reconsidered.
A natural question, therefore, is whether there are any unbreakable cryptosystems, and, if so, why aren’t they used all the time?
The answer is yes; there is a system, known as the one-time pad, that is unbreakable. Even a brute force attack will not yield the key. But the unfortunate truth is that the expense of using a one-time pad is enormous. It requires exchanging a key that is as long as the plaintext, and even then the key can only be used once. Therefore, one opts for algorithms that, when implemented correctly with the appropriate key size, are unbreakable in any reasonable amount of time.
An important point when considering key size is that, in many cases, one can mathematically increase security by a slight increase in key size, but this is not always practical. If you are working with chips that can handle words of 64 bits, then an increase in the key size from 64 to 65 bits could mean redesigning your hardware, which could be expensive. Therefore, designing good cryptosystems involves both mathematical and engineering considerations.
Finally, we need a few words about the size of numbers. Your intuition might say that working with a 20-digit number takes twice as long as working with a 10-digit number. That is true in some algorithms. However, if you count up to , you are not even close to ; you are only one 10 billionth of the way there. Similarly, a brute force attack against a 60-bit key takes a billion times longer than one against a 30-bit key.
There are two ways to measure the size of numbers: the actual magnitude of the number , and the number of digits in its decimal representation (we could also use its binary representation), which is approximately The number of single-digit multiplications needed to square a , using the standard algorithm from elementary school, is , or approximately The number of divisions needed to factor a number by dividing by all primes up to the square root of is around . An algorithm that runs in time a power of is much more desirable than one that runs in time a power of . In the present example, if we double the number of digits in , the time it takes to square increases by a factor of 4, while the time it takes to factor increases enormously. Of course, there are better algorithms available for both of these operations, but, at present, factorization takes significantly longer than multiplication.
We’ll meet algorithms that take time a power of to perform certain calculations (for example, finding greatest common divisors and doing modular exponentiation). There are other computations for which the best known algorithms run only slightly better than a power of (for example, factoring and finding discrete logarithms). The interplay between the fast algorithms and the slower ones is the basis of several cryptographic algorithms that we’ll encounter in this book.
