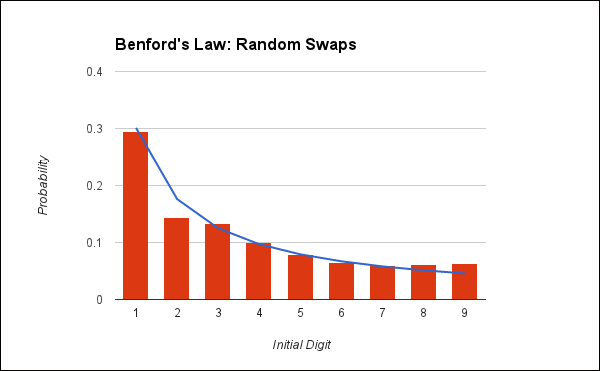
So far, we've seen several datasets, all of which conform to Benford's Law, most of them quite strongly. We haven't yet seen a dataset that does not conform to this distribution of initial digits. What would a failing dataset look like?

There are many ways in which we could get data that doesn't conform. Any linear data, for example, would have a more uniform distribution of the initial digits. However, we can also simulate fraudulent data easily, and in the process, we can learn just how much noise a dataset can handle before Benford's Law begins to have trouble with it.

We'll start this experiment with the population data that we looked at earlier. We'll progressively introduce more and more junk into the dataset. We'll randomly replace items in the dataset with a random value and re-run incanter.stats/benford-test on it. When it finally fails, we can note how many items we've replaced and how far off the new distribution is.

The primary function is shown as follows. There are a few utilities, and you can look into the code download for their definitions:

(defn make-fraudulent
  ([data] (make-fraudulent data 1 0.05 1000))
  ([data block sig-level k]
   (let [get-rand (make-rand-range-fn data)]
     (loop [v (vec (sample data k)), benford (s/benford-test v),
            n 0, ps [], swapped #{}]
       (println n . (:p-value benford))
       (if (< (:p-value benford) sig-level)
         {:n n, :benford benford, :data v, :p-history ps,
          :swapped swapped}
         (let [[new-v new-swapped]
               (swap-random
                 v swapped #(rand-int k) get-rand block)
               benford (s/benford-test new-v)]
           (recur new-v benford (inc n)
                  (conj ps (:p-value benford))
                  new-swapped)))))))

This function is primarily a loop. At each step, it checks whether the p-value is low enough to declare the job as finished. If so, it returns the information it has collected so far.

If this isn't done, it swaps out block indexes, recomputes a new p-value, and stores the information it tracks.

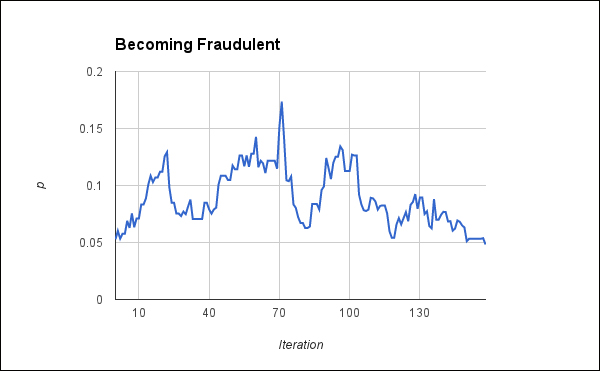
This isn't a particularly efficient process. It is essentially a random walk over the data space. Sometimes, it actually improves the sequence's fit. However, because there's more space that isn't close to the probabilities that Benford's Law predicates for the digits, the values eventually wander off into areas with worse fit and lower p-values. The following is a graph from one run that began with a p-value around 0.05. Instead of immediately dropping below 0.05, it goes up to about 0.17 before finally and gradually, dropping below 0.05 around the iteration number 160.

Looking at the final data from this process is also interesting. It's really not as different from the regular Benford's curve as you might expect it to be. It appears that the problem has too few twos and too many eights and nines.