6
Addition and Subtraction: Basic Facts/Number Combinations
One of our key beliefs is that interventions must have mathematical structure and credibility.
Introduction
If you ask dyslexic or dyscalculic children, or indeed any child, to add 8 and 7 and explain how they reached their answer you will get a selection of methods, depending on each child’s experiences and own idiosyncratic ideas. Ackerman et al. (1986) call them ‘inconsistent’, for example:
- Counting all: the child counts to 8 and then counts on the 7 (probably counting on fingers or on objects in the room).
- Counting on: the child holds 8 in his head and counts on 7 counting through 9 to 15 (again, probably counting on fingers or on objects in the room). This strategy is prone to the common error where the child starts counting at 8.
- Using 10: the child breaks 7 into 2 + 5, uses the 2 with the 8 to make 10, then adds 5, or works via 7 + 3.
- Using doubles: the child uses (2 × 8) − 1 or (2 × 7) + 1.
- Straight recall: the child ‘just knows’.
Carpenter and Moser, quoted in Thompson (1999) identify five levels of sophistication of addition strategies used by young children when solving simple word problems:
- Count all.
- Count on from the first number.
- Count on from the larger number.
- Recall/retrieval of a known fact.
- Deriving the fact from a known fact (as in using 5 + 5 to access 5 + 6).
In their research on basic addition, Gray and Tall (1994) observed that children rated as above average in maths by their teachers either accessed facts by direct recall or used ‘mathematical’ strategies to work them out, often very quickly. The children rated as below average had poor recall and little or no use of these compensatory strategies. The above average group rarely used counting. Counting was the only resort for the below average group.
More recently there has been an increased interest from researchers such as Torbeyns et al. (2004) and Smith and Teague (2014) in children’s use of strategies, although some have only looked at a limited range of strategies. Generally speaking, these studies suggest that children with learning difficulties in maths, not surprisingly, continue to use the counting‐on strategy longer than their age equivalent ‘normal’ peers. Torbeyns et al. comment on the potential benefits that: ‘early and frequent intervention directed toward facilitating the development of these children’s procedural skills might reduce the difference in the rate of development.’ If children are left to devise their own survival strategies, then we must not be surprised if these lack mathematical sophistication; nor must we be surprised if it is very difficult to replace these established methods with new ones. In other words, the intervention should start before it is needed. It should be pre‐emptive and based on what we know about the reasons for children to start to fail in maths.
It is of note that, increasingly in the USA, the term arithmetic, or number combinations is replacing the term number facts (Gersten et al., 2005) recognising that the ‘facts’ are not always accessed by simple retrieval.
In this chapter we will look at strategies for working out basic facts efficiently and in ways that enhance and interrelate numbers, number concept, concept of ten and place value and facility with number and number operations. We are assuming that a child will have great difficulty in rote learning the facts and, even if he should succeed, difficulty in holding those facts in memory for more than a few hours. Threlfall and Frobisher (1999) argue that ‘the short‐term gains that give rote learning its appeal are illusory and are less efficient in the longer term’ and we should note that Threlfall and Frobisher are not referring to a special needs population, where their comments are even more apposite. Children will be able to access more facts if they have strategies to use when memory fails them and leaves them with no way to obtain an answer, that is, helpless. Some strategies will be used in their entirety by a child, but others will be mastered to the stage where they become memory ‘hooks’ and are only used in part to supplement a half‐known fact and give a security in the validity of the answer. Since the strategies involve the same key facts each time, this procedure automatically rehearses these key facts over and over again. However, just because we choose to label them ‘key’ facts does not mean they are guaranteed a secure place in long‐term memory.
The strategy of counting on is an ineffective strategy beyond counting on one or two or maybe three. It is a method that requires too much time to operate and it tends therefore, to be susceptible to poor short‐term memory and may overload working memory. It is also susceptible to counting errors. Furthermore, it does not support number concept or the relationships between numbers; neither does it encourage seeing patterns in numbers. We advocate strategies that use number relationships wherever possible. Chinn (1994) looked at the knowledge of basic addition facts presented at four‐second intervals and twelve‐second intervals to a dyslexic population of 11–13‐year‐old students and found that, although dyslexic pupils scored significantly less well than a mainstream population in the four‐second addition task, their scores in the twelve‐second addition task were virtually equivalent. This is not surprising, as one would expect any of the facts asked to be accessible in twelve seconds by finger counting (although other strategies were used by both groups).
The relative ease, and accuracy, of counting on in ones as a strategy for accessing addition facts may be a major contributor to addition being the default operation for many learners (Chinn, 2013). Counting back in ones is often done for subtraction, less efficiently. Counting forwards and backwards in other numbers, say three, is even less efficient for multiplication and division facts.
It is easy to underestimate just how much early experience and information a dyslexic or dyscalculic student has missed, which makes it difficult to know how far back to go when starting a teaching programme. One of the key ideas that this chapter advocates is the breaking down and building up of numbers. So, if a child did not receive and absorb work such as looking at 6 as in Figure 6.1, then strategies which suggest that 8 + 6 can be added as (8 + 2) + 4 will be less easy to teach (or learn). As ever, you have to ‘read’ the child to know how much material to provide. Ashlock (2010) provides an excellent range of teaching ideas to develop and reinforce algorithms and concepts.
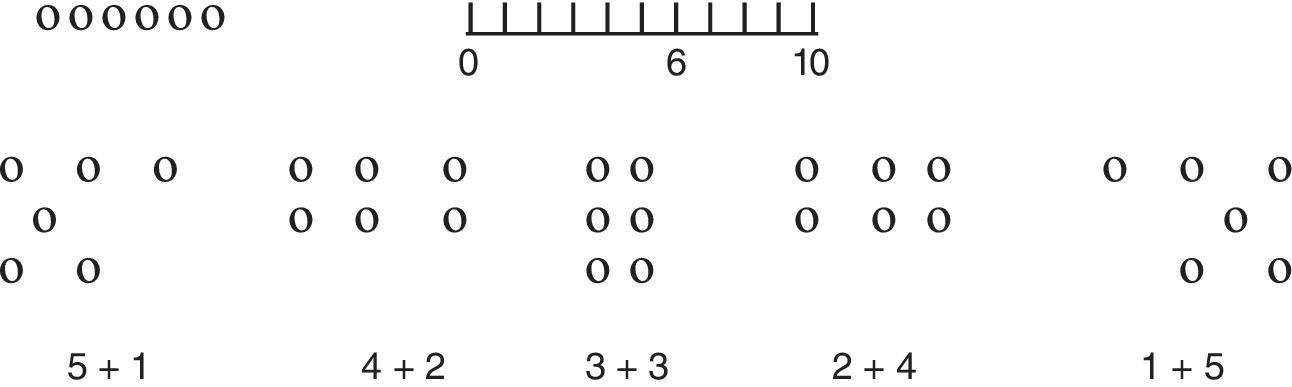
Figure 6.1 Visual images for six.
Strategies for Learning/Remembering the Addition and Subtraction Facts
The basic addition facts, which convert to the basic subtraction facts, from 0 to 10 can be arranged in a square (Figure 6.2; see also the times table facts square). This gives the child a task of rote learning 121 addition and 121 subtraction facts or developing strategies for as many of these facts as possible. Viewing this statement in isolation makes it seem a daunting task. Indeed, viewing that density of information as presented in the square at one time can be a daunting task. One of the great characteristics of maths is that you can use the interrelationships between facts and operations to significantly reduce the size of tasks such as this one.

Figure 6.2 The addition and subtraction facts square.
The procedure for addressing the addition/subtraction facts task is similar in technique to the one that will be used for times tables. It uses patterns, the interrelationships between numbers and operations and the ability to break down and build up numbers, using the core/key numbers (0, 1, 2, 5, 10). It builds on strategies that the children themselves sometimes use, but organises and rationalises idiosyncratic ideas. It adds structure and pattern. The presentation as a square of facts gives some motivation in that initial gains can be shown convincingly and as quickly achieved, by shading in ‘known’ facts. The strategies are widely applicable and mathematical rather than being a collection of one‐off ‘tricks’, rhymes or mnemonics. It is not the purpose to overwhelm the learner by presenting all this information in such a concentrated way at one time. It is to provide motivation by demonstrating progress.
Even though we discuss subtraction after working on the addition aspect of these facts, we feel it is most important to emphasise the subtraction ‘side’ of the addition fact as each fact is discussed. As ever, teachers use their judgement to decide what constitutes a counterproductive overload of information. However, this has a developmental attribute, for example leading to early experiences of algebra:
The zero facts: n + 0 and 0 + n
Many years of experience in the classroom has taught us that zero will create problems.
The collection of facts, n + 0 and 0 + n, can be demonstrated using, for example, counters in boxes.
- An empty box is shown to the child and, after discussion about the contents and zero, the symbol 0 is written on the screen, white board or a sheet of paper.
- Five counters are added to the box. + 5 is written on the screen/board/paper, giving 0 + 5.
- The child counts the number of counters in the box, 5.
- The written form now is 0 + 5 = 5.
A similar procedure may be used to deduce 5 + 0 = 5. Careful and appropriately focused use of language is needed if later confusion with × 0 facts is to be pre‐empted.
Much of ‘early’ maths is better taught when the need to pre‐empt future confusion is addressed.
This establishes 21 facts, though, as is ever the case, an unusual or new presentation of a ‘known’ fact may confuse the child. A typical error occurs in addition sums such as
The subtraction of zero should be demonstrated, discussed and presented in symbols.
Adding on 1 and 2
This can be introduced by asking the child to look at a number line and handle counters or a bead string (Figure 6.4), so that he sees, say, 4 + 1 as one move on the number line, that is, a move to the next number, one counter added (Figure 6.3), one bead moved. For adding one, the child has to ‘see’ the process as simply moving to the next number by adding one object each time and the reverse by subtracting/taking away one object each time.

Figure 6.3 The number patterns for 1–10.

Figure 6.4 The bead string set up to show 8 + 2.
A very similar argument applies to adding 2, although the child may have to physically and orally count on the two numbers. This should still be quick and accurate. A knowledge of the even and odd numbers will support this operation and encourage the appraisal of answers. The child can practise counting in twos, starting from different numbers. The child will then need to spend some time looking at facts such as 1 + 9 and 2 + 5, with the teacher leading him into the commutative properties of 1 + n = n + 1 and n + 2 = 2 + n and teaching that it is quicker, less prone to error and more effective to count the smaller number onto the bigger number.
If this can be accomplished, then 36 more fact squares can be shaded in on the addition square, a total of 57, leaving 64 to go.
Adding to ten; adding on ten
It is often the case when working with dyslexics and dyscalculics that a lesson has more than one goal. The subsidiary goal is usually a review of a previously ‘learned’, and often ‘forgotten’, fact or concept. In this case the forgotten concept is likely to be place value. If this is re‐established, then adding on to 10 is taking the learner back to the first family of basic addition facts, that is, n + 0 and 0 + n and extending it to n + 10 and 10 + n partly as a reminder of the place value of digits in numbers.
A teaching idea is to use a place value card and base ten blocks or coins and discuss, do and write the addition in symbols. Number lines and bead strings can be used to offer further illustrations of the procedure.
The pattern in symbols (digits) is:
| 10 + 1 = 11 |
| 10 + 2 = 12 |
| 10 + 3 = 13 |
| 10 + 4 = 14 |
| 10 + 5 = 15 |
| 10 + 6 = 16 |
| 10 + 7 = 17 |
| 10 + 8 = 18 |
| 10 + 9 = 19 and 10 + 10 = 20 |
The tens digit (1) does not change, but the ones digit becomes the same as the added number, 10 + d = 1d (not an algebra term). An extra difficulty sometimes arises from the inconvenient situation that the names of the numbers from 13 to 19, unlike subsequent decades, have the ones digit named first, for example 17. This makes the oral pattern inconsistent in comparison to the next decades. This is a chance to remind learners to be ready for this inconsistency.
If this series of facts is understood and absorbed then the task has reduced to 49 facts.
Use of doubles
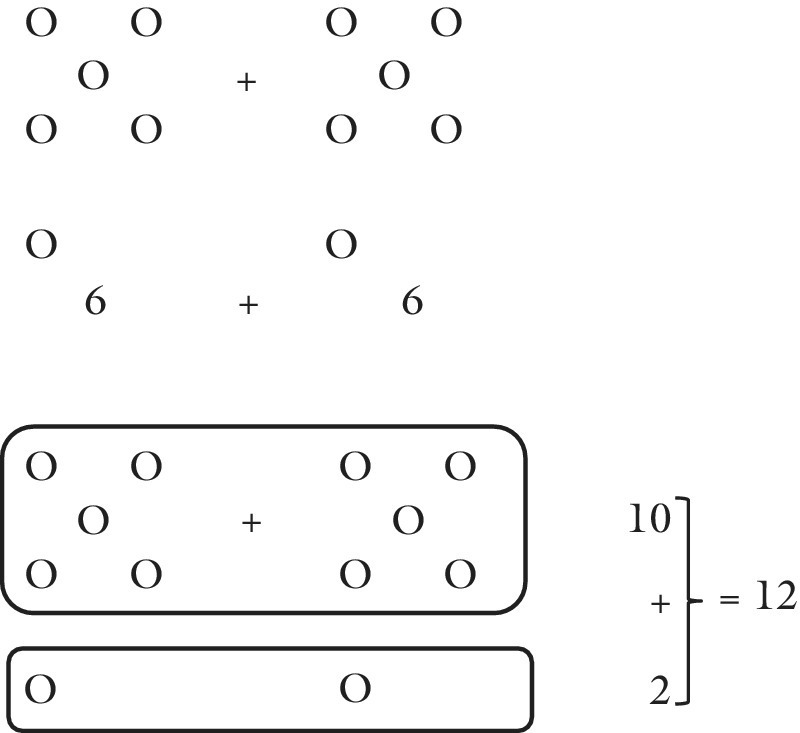
For addition facts, children often know the doubles. Similarly, in multiplication they often know the squares. Many children also use them to derive other addition facts, for example, 8 + 7 is often seen as double 8 less 1 or as double 7 plus 1.
Two sets of counters provide a good representation of the derivation of these facts, using the core patterns for the arrangements, for example, 6 + 6.
Cuisenaire rods are also useful, for example two seven rods are placed side by side and 7 + 7 is written and discussed as being equal to 14. A one rod is placed on the end of a seven rod, increasing the sum to 15 (adding on 1 takes you to the next number). The seven and one rods are exchanged for an eight rod and the addition 7 + 8 = 15 can be discussed, maybe using the ever‐useful question, ‘Is this bigger or smaller?
| (2 + 2) + 1 = 2 + 3 = 3 + 2 = 5 |
| (3 + 3) + 1 = 3 + 4 = 4 + 3 = 7 |
| (3 + 3) − 1 = 3 + 2 = 2 + 3 = 5 |
| (4 + 4) + 1 = 4 + 5 = 5 + 4 = 9 |
| (4 + 4) − 1 = 4 + 3 = 3 + 4 = 7 |
| (5 + 5) + 1 = 5 + 6 = 6 + 5 = 11 |
| (5 + 5) − 1 = 5 + 4 = 4 + 5 = 9 and so on. |
This gives 7 facts for the doubles and 12 facts for doubles ±1. The total task is down to 30 facts, half of which are commutative, so there are 15 different facts to go.
Again there is an opportunity here to look at the concept of odd and even numbers and at the basic rules about combining numbers.
The doubles are core basic facts.
Number bonds/combinations for ten
This family of facts has significant uses in other situations to solve other problems. They are therefore important and are core facts to learn. To put this in another way, if a child has difficulty in rote learning facts, then let him focus his learning on the facts that are going to be of most use.
There are a variety of concrete images which can be used to illustrate the number bonds to ten.
- Cuisenaire rods (Figure 6.5) give a colourful image of the linear relationship and the commutative property.
- A ten‐bead bead‐string is excellent for the concept of the conservation of ten and also for the commutative property, simply by turning the string around.
- The number bonds/combinations can be written graphically, as in Figure 6.6. This was also shown in Chapter 5 (Figure 5.12).
Figure 6.5 Cuisenaire rods.

Figure 6.6 Different font sizes to illustrate the number combinations for ten.
Note: A learner can be taught to write a normal sized digit version of this series quite quickly, 0 to 10 on top of 10 to 0, with 5 and 5 having to be aligned as a check, at the top of an exam paper, removing stress when the facts are needed within the exam.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Whatever materials the child handles, or visual images he sees, you must make sure that the digits are presented with each aid so that the link is made between the material or the visual representation and the symbols.
Although this section collects together the number bonds/combinations for 10, only 6 + 4, 4 + 6, 7 + 3 and 3 + 7 are ‘new’ facts, so, 26 to go out of the 121.
The number bonds/combinations for ten are core facts.
Number bonds/combinations for nine
It is valuable to link these to the number bonds for ten. They are important as part of the strategy for the nine times table facts and for continuing the processes of learning to interrelate numbers and estimation. The child is guided to see that nine is one less than ten, so the two sets of number bonds need to be compared and the consistent relationship and pattern emphasised.
The example below shows 6 + 4 compared to 6 + 3 and 5 + 4

Adding on nine
Adding on nine also follows on from the facts for ten. This collection of facts is also useful as an early example of estimation. The child is learning again that ten is one more than nine and that nine is one less than ten. The question to use when comparing the addition of nine to the addition of ten is again, ‘Is the answer bigger or smaller?’
The child can practise the addition with coins, Cuisenaire rods or base ten blocks, comparing adding ten with adding nine, looking at adding nine by adding ten then subtracting one, or using the added number to provide one to make the nine up to ten and thus making the added number one less, for example:
These two groups of nine facts add twelve more facts, leaving fourteen to go.
Sharing doubles
Algebra can be an easy and illustrative way of writing a generalisation, though we are not saying this is a good idea for seven‐year‐old pupils.
So n + n is the same as (n − 1) + (n + 1). There are six of these facts left that have not been dealt with elsewhere:

Again these facts can be experienced by moving counters between two initially equal patterns. The strategy is an example of the conservation of number and is worth inclusion for this learning objective alone.

There are eight facts to go. The commutative property reduces this to four: 8 + 3, 8 + 4, 8 + 5, 7 + 4.
Adding onto 8 can be achieved via 10, for example 8 + 5 becomes (8 + 2) + 3.
7 + 4 can be seen as one more than the number bond 7 + 3.
Overview
Some of the facts/combinations described in this chapter fall into more than one strategy group. As flexibility is important, this gives the child some choice of method. Shading squares on the addition fact table for families of strategies can emphasise the pattern of each relationship.
In each strategy there is ample scope to enable the child to use concrete manipulative materials and visual images. These materials and images must be used, as ever, in conjunction with the written numbers. The materials and images are of no use if they are not automatically linked in the child’s mind to the symbols for the quantities they represent. Also, the child has to learn to progress from the concrete to the visual to the symbolic.
When writing and talking about the addition facts, you must use more than one format and vary the vocabulary without creating confusion, for example, 4 + 6 = 10 can be phrased as:
- What is 4 add 6?
- What adds on to 4 to make 10?
- Can you find the ‘right’ number to fit into the boxes?
The latter two examples are leading the child to see subtraction as ‘adding on’. So, 4 + 6 = □ is a straight addition fact. The child is, however, learning that ten can be split into two constituent parts, in this case four and six. With 4 + □ = 10 and □ + 6 = 10 the child still has to know that we are looking at two parts, but he now knows the total and only one of the parts. We are changing the frame of reference, not the knowledge. The child is learning the adaptability of mathematics facts.
Subtraction Facts
Although the subtraction facts should be discussed alongside the addition facts, there will probably be a need to reinforce this material. From informal surveys when lecturing to adults on teaching arithmetic, we know that the perception of subtraction is that it is a harder operation than addition. This has been confirmed with analysis of the data collected to standardise Chinn’s (2017a) ‘15 minute test’ from More Trouble with Maths.
Further examples and the introduction of the vocabulary of subtraction (minus, subtract, take away, etc.) should help the child to translate his addition facts into subtraction facts. The idea of a total or sum and two parts or addends will be used in ‘harder’ subtraction problems in the next chapter.
The child needs to learn that addition and subtraction are variations of the same process (Chinn and Ashcroft, 1992; 2004). The ideas above provide the framework which you can use and develop into an instructional format.
Extension
We (Chinn and Ashcroft, 1992; 2004) have long been advocates for the use of patterns and sequences to support memory. For example, the addition fact 4 + 7 can be extended to the sequences/patterns:
| 4 + 7 = 11 | 4 + 7 = 11 |
| 4 + 17 = 21 | 14 + 7 = 21 |
| 4 + 27 = 31 | 24 + 7 = 31 |
| 4 + 37 = 41 | 34 + 7 = 41 |
| 4 + 47 = 51 | 44 + 7 = 51, etc. |
These patterns show the consistent contribution of 4 + 7 to a sequence of additions. We have found that our dyslexic learners often need the aspects of this pattern (and similar patterns) pointing out. In doing this, you are also leading the child towards more challenging addition problems, where he will be using the addition facts and, it is hoped, reinforcing his knowledge of these facts.
