3
Cognitive (Thinking) Style in Mathematics
Introduction
We use the term cognitive (or thinking) style in mathematics to refer to the way a person thinks through a problem. Allport (1937, quoted in Riding and Rayner, 1998) describes cognitive style as a person’s typical or habitual mode of problem solving, thinking, perceiving and remembering. We have the optimistic attitude of many teachers and would challenge the word ‘habitual’. Mathematically, its history can be dated back as far as Descartes (1638, cited in Krutetskii, 1976), who described two styles of problem solver. The first solves problems by a succession of logical deductions, whilst the second uses intuition and immediate perceptions of connections and relationships. These two contrasting styles are described again in later literature. Boltevskii (1908, cited in Krutetskii, 1976) and Harvey (1982) labelled the two styles geometers and algebraists, where the algebraist links most closely to the logical, sequential thinker and the geometer to the intuitive style. Kovalev and Myshishchev (in Krutetskii, 1976) used the term ‘intuitive’ to describe a person who is not conscious of every step in his thought processes, but who perceives essential connections more clearly and quickly than his complementary stylist, the ‘discursive’ thinker. Skemp (1981 and 1986, also Choat, 1982) describes relational and instrumental understanding. Marolda and Davidson (2000) describe ‘Mathematical Learning Profiles’ looking at how students learn and how teaching can be differentiated to meet preferred profiles
Although in his classic book How to Solve It, Polya (1990) identified four styles of problem‐solver, the four can readily be combined in pairs, reducing them to two distinct styles. Polya called the four styles groping, bright idea, algebra and generalisation. The first two describe intuitive thinkers and the last two describe sequential thinkers. This reduction down to two distinct styles seems a possibility for all models of thinking styles.
More recently, Kahneman (2011) described two modes of thinking: ‘System 1 operates automatically and quickly, with little or no effort and no sense of voluntary control. System 2 allocates attention to the effortful mental activities that demand it, including complex computations. The operations of System 2 are often associated with the subjective experience of agency, choice and concentration.’ Kahneman uses a maths example, working out 17 × 24, to illustrate the modes and provides a further example of the interaction of the many factors that are involved in doing maths: ‘Your muscles tensed up, your blood pressure rose and your heart rate increased. Someone looking closely at your eyes while you tackled this problem would have seen your pupils dilate.’
In terms of learning, Riding and Cheema (1991) provided a good overview of cognitive styles as applied to all areas of learning. Duffin and Simpson (2006) suggested four types of mathematical learners: alien (preference for absorbing new information without trying to link it with the existing knowledge), natural (preference for integrating new and old knowledge in a coherent ‘global’ structure), coherence (preference for finding a ‘local’ structure in the new knowledge) and flexible (preference for adopting different ways of thinking depending on the situation).
There is an obvious overlap here with meta‐cognition. Returning to How People Learn (Bransford et al., 2000), the third key finding is: ‘A “metacognitive” approach to instruction can help students learn to take control of their own learning by defining learning goals and monitoring their progress in achieving them.’ Taking a perspective that is broader than just thinking style Mortimore (2008) provides an excellent overview of learning styles and dyslexia.
We believe that the reality is that people use flexible cognitive styles. This belief is not rocket science.
Qualitative and Quantitative Style
Sharma (1986; 1989) identified and labelled two extreme styles of learning personalities (again taking a broader construct than thinking style) as quantitative and qualitative. The characteristics of the quantitative style are essentially sequential/logical and those of the qualitative are intuitive and holistic. Sharma also suggested that most personalities lie on a continuum between these two extremes. He used the order in which the Rey Osterrieth Complex Figure is copied as one of the instruments to diagnose the preferred learning personality. This figure (Figure 3.1) is detailed and Sharma looks to see if the detail takes precedent over the outline, or vice versa, when the figure is reproduced.
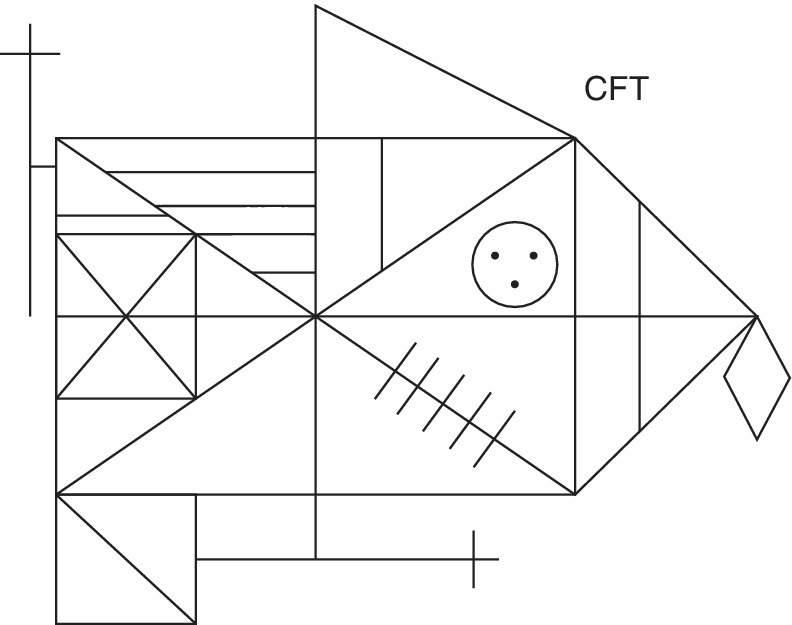
Figure 3.1 The Rey Osterrieth Complex Design Test.
Sharma’s qualitative learner approaches problems holistically and is good at recognising patterns. He uses an intuitive approach, tends not to show his working and does not like practice exercises. This contrasts with the quantitative learner, who processes information sequentially, looking for formulae, methods and ‘recipes’. This learner attempts to classify problems into types and to identify a suitable process to use in solving the problem.
It is worth noting that the intuitive style is not always viewed favourably. For example, Skemp (1971) considered it a hit‐and‐miss method, a method that is not always reproducible. Most people have experience of the teacher who says, ‘I am not marking that mathematics until I can see some method written down.’ (Whilst there are some very valid reasons for this to be a reasonable comment, it can indicate a lack of understanding of thinking style.)
The brain
The rapid and dramatic advances in ways that the brain can be studied have changed much of what we thought we knew in the earlier editions of this book. The broad characterisation of behaviours as left brain and right brain may well have to be abandoned. So we will take what we wrote in those editions as an historical introduction.
Some writers have linked cognitive style to hemispheric specialisation. Kane and Kane (1979) suggested the roles played by each hemisphere in a variety of different modes. For thinking, the right brain is described as deductive, divergent, intuitive, holistic, relating to concepts, simultaneity and geometry, whilst the left brain is described as inductive, convergent, segmented, logical and algebraic. Wheatley (1977) and Wheatley et al. (1978) linked problem‐solving styles with left and right brain specialisations. He described the right brain as all‐at‐once and gestalt and the left as one‐at‐a‐time and serial. Wheatley also concluded that a good problem solver achieves a smooth integration of the two modes of thinking.
The interpretation (or speculation) as to what the brain is doing is of interest, in that it gives a neurological perspective on different thinking styles. It seems somewhat dismissive to describe the ‘global’ thinker as intuitive, which seems to infer little conscious thought (though see Kahneman’s System 1), when the intuitive process is probably based on rapid consideration of possibilities, experiences and knowledge rather than being a sort of inspired, unconsidered guess.
Even when our knowledge of the brain was in its infancy Springer and Deutsch (1993) added notes of caution to those who claim that schools fail to educate the right side of the brain: ‘But are these right‐hemisphere functions? We do not think it is as simple as that and there is certainly no conclusive evidence to that effect. Our educational system may miss training or developing half of the brain, but it probably does so by missing out on the talents of both hemispheres.’ Pioneering work by cognitive neuroscientists such as Bugden and Ansari (2015) is now offering the possibilities of detailed and accurate studies of the brain at work and the scope of neuronal plasticity.
Although the location of brain activity is a fascinating area which modern technology is making more accessible to investigation, the way the student presents in class, his observable behaviours, may provide enough information for a teacher when planning appropriate responses and interventions. Cognitive style is often easy to identify if teachers just take time to observe the student as he works and possibly to reinforce those observations with some carefully chosen diagnostic questions and comments.
Cognitive (Thinking) Style in the Classroom
The work of Bath and Knox (1984) and Bath et al. (1986) on cognitive style arose from work and observations in the classroom, more specifically from teaching dyslexic (and probably dyscalculic) children of secondary school age. It therefore has its roots in the observation of children with specific learning difficulties as they studied mathematics. Bath et al. labelled the two extremes of the continuum of cognitive styles as grasshoppers, basically intuitive and answer oriented, and inchworms, basically step by step and formula oriented. The characteristics of the two styles are summarised in Table 3.1 (Chinn, 2004) by looking at the three stages of solving a problem: identification, solving and verification.
Table 3.1 Cognitive styles of the inchworm and the grasshopper.
| Inchworm | Grasshopper | |
| First approach to a problem (identification) | 1. Focuses on the parts and details. | 1. Overviews, holistic, puts together. |
| 2. Looks at the numbers and facts to select a suitable formula or procedure. |
2. Looks at the numbers and facts to estimate an answer, or narrow down the range of answers. Uses controlled exploration. This is far more cerebral than guessing. |
|
| Solving the problem | 3. Formula, procedure oriented. | 3. Answer oriented. |
| 4. Constrained focus. Uses one method. | 4. Flexible focus. Uses a range of methods. | |
| 5. Works in serially ordered steps, usually forward. | 5. Often works back from a trial answer. | |
| 6. Uses numbers exactly as given (numerically literal). | 6. Adjusts, breaks down/builds up numbers to make the calculation easier. | |
| 7. More comfortable with paper and pen. Documents method. | 7. Rarely documents method. Performs calculations mentally (and intuitively). | |
| Checking and evaluating answers (verification) | 8. Unlikely to check or evaluate answers. If a check is done it will be by the same procedure/method. | 8. Likely to appraise and evaluate answers against original estimate. Checks by an alternate method/procedure |
| 9. Often does not understand procedures or values of numbers. Works mechanically. | 9. Good understanding of number, methods and relationships. |
The teacher’s role
Bath et al. (1986) investigated cognitive style by classifying answers to a series of carefully designed mathematics questions, thus directly taking into account how a child actually does mathematics. One of the main recommendations of our book is the necessity for teacher and child to be flexible in their approach to mathematics – Krutetskii (1976) uses the wonderful word ‘harmonious’ to describe the blending of styles – yet to be aware that learners (and teachers) may not always achieve this goal. Sharma (1989) commented on the need for teachers to be aware of cognitive style:
All of us show and use different and unique mixtures of the two (personalities) but one approach is more dominant than the other in different individuals. And that is what the teacher should be aware of almost constantly. Since you, the teacher, are usually in the controlling role, then the source and sanction for this flexibility must come predominantly from you.
This situation is well expressed by Cobb (1991): ‘We do not mean to imply that the teacher’s beliefs are simply transferred to the student. Rather, the teacher has the authority to legitimise what is acceptable and to sanction what is not acceptable.’
The structure of mathematical abilities
Krutetskii (1976), in presenting a broad outline of the structure of mathematical abilities during school age, specifies a need for flexible thinking and some other skills which dyslexics and dyscalculics may find difficult. He specifies:
- The ability for logical thought in the sphere of quantitative and spatial relationships, number and letter symbols; the ability to think in mathematical symbols.
- The ability for rapid and broad generalisation of mathematical objects, relations and operations.
- Flexibility of mental processes in mathematical activity.
- Striving for clarity, simplicity, economy and rationality of solutions.
- The ability for rapid and free reconstruction of the direction of a mental process, switching from a direct to a reverse train of thought.
- Mathematical memory (generalised memory for mathematical relationships), and for methods of problem solving and principles of approach.
- These components are closely interrelated, influencing one another and forming in their aggregate a single integral syndrome of mathematical giftedness.
Although Krutetskii makes these observations concerning giftedness in mathematics, they are equally apposite for competence and for avoiding failure. The reader can see within these observations where dyslexics and dyscalculics may typically be at a disadvantage and where learning difficulties may create problems.
There are other sources of support for different learning styles (e.g. and in more general terms, de Bono, 1999), but the emphasis of the remainder of this chapter is to paint a clearer picture of the background reasons for, and consequences of, different cognitive styles in mathematics.
Thinking styles
To expand and clarify the picture of the two extremes of the cognitive style continuum, consider some mathematics problems and the solutions which an inchworm and a grasshopper might use. There is no implied value judgement on the two (extremes) of style. Indeed Kubrick and Rudnick (1980) suggested that teachers should encourage a wide variety of approaches, ideas and solutions. As has been already quoted, Krutetskii looks for a ‘harmonious’ approach. If for no other reason, the ability to generate more than one way of solving a problem allows the student to be more effective when checking his own work.
Examples
Some of the questions below are taken from the Test of Cognitive Style in Mathematics (Bath et al., 1986) now included in Chinn’s (2017a) book on diagnosing and assessing mathematical learning difficulties. When using questions such as these with learners, the key diagnostic question is, ‘How did you work that out?’ or, ‘How did you do that?’ A supplementary question that explores the flexibility in problem solving skills is, ‘Can you think of another way of doing this problem?’
An inchworm will see first the 2 and the times sign. He tends not to overview the problem. Also he tends to take the problem ‘literally’, that is, if it says 2 × 4 × 3 × 5, then that is the order and it is not to be changed, and since 2 is an easy times table, he will begin: 2 × 4 = 8.
The next stage may be a little more challenging for times table facts, but 8 × 3 = 24.
The last stage (24 × 5) may be too much of a challenge because of the load on working memory in multiplying 4 by 5, remembering that the ones digit is 0, carrying the 2, holding it in memory while multiplying 2 by 5, remembering the 2, knowing where to incorporate it, remembering the ones digit 0 and putting it all together to give 120. Some children will just say ‘That’s as far as I can get.’
A grasshopper, especially if he knows he has limited times table knowledge, will overview the problem, reading through to the end to see if there are any short cuts or easy strategies or rearrangements. He may also be trying to get an estimate of the value of the answer.
He is likely to rearrange the problem to (3 × 4) × (2 × 5), that is, 12 × 10 = 120. Thus he has taken a more global and flexible view of the question. In doing so he has reduced the demand on his times table knowledge and the load on his working memory.
An inchworm with some algebra skills will develop an equation:
Let the first number be n:
- then the second number is n + 1
- and the third number is n + 2.
So n + (n + 1) + (n + 2) = 60 which is then solved:
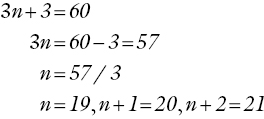
The three numbers are 19, 20 and 21. The process is logical and sequential and is (effectively) independent of the value of the numbers involved; it will work for any similar problem. It takes the solution almost directly from the way the question is presented.
An inchworm without algebra skills will find it difficult to make a reasonable guess at a starting number. His subsequent adjustments to his guess will most probably be step by step, one at a time. So if his first guess is 10, his next guess is likely to be 11, irrespective of and without any appraisal of the answer generated with 10.
A grasshopper will start with a controlled exploration, leading to an estimate. He will see that the three numbers are approximately equal and that a good estimate of their value is given by 60/3 = 20. It is only a short and easy step (easy for the grasshopper, but not necessarily as easy for the numerically literal inchworm) to 19, 20, 21. Again the strategy is holistic/global and peculiar to these numbers. It is an answer‐oriented strategy.
How many squares in Figure 3.2 are black?

Figure 3.2 The squares.
The pattern of 7 × 7 squares in Figure 3.2 is not equally divisible into black and white squares, which makes the problem less straightforward.
The inchworm will probably resort to counting each square, thus focusing on the parts of the square.
In a formula mode, an inchworm may see a square, count the number of black squares on each side as 4, multiply 4 × 4 and say ‘16’. Sometimes if the tester says, ‘49 squares and 16 are black?’ hinting that 16 does not match the almost half relationship. The inchworm will feel secure in the use of the formula (4 × 4 = 16) for a square and not see the obvious inaccuracy of the solution.
The grasshopper is holistic in his initial overview. The 7 × 7 squares make 49 and ‘half’ will be seen to be 25 since observation (of the corners or number of black rows) shows that the larger number of squares are black.
This problem illustrates the ‘whole to parts’ against the ‘part to whole’ contrast in the two styles.
The inchworm will rewrite the sum in vertical form:
The addition may be carried out with tallies to mark progress and help the child keep count as he moves down the numbers. The child is unlikely to use a pre‐estimate or a check.
The inchworm will work in the order in which the numbers are given.
The grasshopper is likely to look for pairs and clusters of numbers which add to 10 or 20, for example in the ones column there is 7 + 3 = 10 and 9 + 6 + 5 = 20. In the tens column there is 3 + 3 + 4 = 10 and from 8 + 1 + 3 (carried from units) he can extract 8 + 2, leaving 2. Answer 220.
The grasshopper will probably have already grouped 85 and 19 as a little over 100 and 36, 37 and 43 as a bigger bit over 100, estimate 200 and a bit. He is using numbers as parts of a whole, where the whole is 10 or 100 or 1000. He is taking the numbers out of the order in which they are presented.
Inferences from the examples
These examples are used to show how learners with the two styles approach problems. Our experience of teaching dyslexic and dyscalculic students leads us to some observations:
- There are some learners at the extremes of the continuum.
- An individual learner may (and should) use both styles sometimes for different questions and sometimes for the same question.
- The style an individual learner uses can depend on the type of question or even on the level of difficulty of the same type of question.
- The type of compensatory strategy (e.g. finger counting or inter‐relating facts) that is used relates to cognitive style.
- Prescriptive curricula create more inchworms than grasshoppers.
- Inchworms with a poor memory for basic facts and procedures are at risk in mathematics.
- Inchworms with a poor working memory are at risk in mathematics.
- Insecure learners are more likely to favour the inchworm style.
- Grasshoppers in the school system need to learn how to document their work.
- Inaccurate grasshoppers are at high risk in mathematics.
- Some questions favour grasshoppers, others favour inchworms, particularly multiple choice questions for grasshoppers.
- Having a dominant style does not mean that the learner is successful in using that style.
- Inchworms want to know ‘How?’ Grasshoppers want to know ‘Why?’
Chinn et al. (2001) in a European study of dyslexic pupils found that, overall, there is a greater tendency for dyslexics to use the inchworm strategies, not because they relate to this thinking style better, but for security and for a perceived minimisation of risk in another manifestation of the tendency to try and avoid errors and thus negative feedback. The study also showed that at that time, before the new Primary Curriculum was introduced in Ireland, the prescriptive nature of the maths curriculum gave the Irish sample a heavy inchworm bias. This would suggest that children can be indoctrinated towards an inchworm thinking style in mathematics by a prescriptive, formula‐oriented curriculum.
You, the teacher, have to be aware of these different styles and the fact that the child may not use the style he has been taught (Hart, 1978) or may, as Duffin (1991) observed, use his own method first and then diligently reproduce for the teacher the standard method he has been taught. Some children may have their enthusiasm for maths crushed if an inflexible cognitive style approach is demanded by the teacher or the curriculum. This is yet another characteristic of learners as individuals, which should warn us that there is no such thing as one method for all.
We could speculate which of the sub‐skill deficits listed in Chapter 2 affect the way a child would solve such problems. For example, poor long‐term memory for basic facts could contribute to a grasshopper style, in that a child may have to overview and combine data in order to avoid facts that he cannot recall. What is clear is that the way a child (or adult) solves a question depends on the blend of deficits and strengths he brings to the problem. You can usually go a long way to finding out how a child solves a problem by asking the simple question, ‘How did you do that?’ This question also encourages meta‐cognition. An interest in how the student is working, rather than a judgement, will be a major source of help for many learners, especially when combined with an awareness of what the child brings to the question.
Contrary to their natural inclination, particularly for examinations, grasshoppers need to learn to know and communicate how they achieved an answer, not just what the answer is. Contrary to their natural inclination, inchworms need to learn, where appropriate, the appropriateness of an answer and why a procedure works.
Zarzycki (2001) explains that almost all school students in Poland are taught only one written method for dealing with the addition, subtraction, multiplication and division of whole numbers. His research supports the claim that there can be detrimental side effects stemming from this restriction in instruction and learning. As mentioned above, our own research with regard to a similar situation in Ireland pre‐1999 also supports this. There is, however, a benefit in having consistency over the years in that parents are not alienated from the way their children are taught mathematics.
Cognitive style and problems
Cognitive style can be used to compensate for some of the difficulties mentioned in Chapter 2. It also can be used to reinforce the connections and links between number facts and between operations and help students interpret word problems. For example, in the question below:
‘Sam wins £96 at bingo and decides to share it equally between his six grandchildren. How much does each child receive?’
At the least sophisticated level of analysis, the word ‘share’ implies that the operation to use is divide. Most children will assume from previous experience that divide will infer a big number divided by a small number, so they will arrive a 96 ÷ 6.
This has now changed a (contrived) real‐life problem into an abstract number statement. An inchworm will try to divide the numbers as they are. It is unlikely to occur to him that both numbers can be divided by 2, making the problem 48 ÷ 3, and, indeed, this may not have made the problem any easier for him.
It is likely that the numbers will be re‐written in the bus stop form 6)96 and a short division attempted (or not attempted, if anxiety takes over). However, if the student has all these skills and facts at his disposal, then the method is effective.
A grasshopper may picture the problem, the £96 being shared out between the six children, visualising the notes and coins being given out in six piles. So, if six £10 notes are given out, then 6 × £10 has been distributed, so £96 − £60 leaves £36 to distribute. Now six £5 notes can be given out, so 6 × £5 has gone, with £36 − £30 leaving £6 to share. So each grandchild has received £10 and £5 and £1, a total of £16. This may be done by variations on this theme, such as sharing £6 as £1 each, which leaves £90 which shares as £15.
The ‘division’ question has been changed into a question about the subtraction of chunks or partial products. It has been re‐interpreted linguistically and mathematically. The student has been able to use facts within his memory bank. An inchworm is highly unlikely to tackle a division problem by involving multiplication.
Teachers and cognitive style
A learner may not have the same cognitive style as his teacher. If neither party is aware of this there are likely to be consequences, not least in communication and in judgement of work. For example, the marks awarded for a method could be affected. Chinn (1995) has carried out a survey of teachers’ marks for three very different methods, which all resulted in a correct answer, used to solve a word problem. The range of marks for each answer varied from 0 to 10 (out of 10), so a child could be with one teacher and receive an encouraging 10 or be with another teacher and score 0 out of 10. The awarding of a particular mark can usually be rationalised by the teachers concerned. This could be a very good reason for a mathematics department to meet and discuss marking policies. Mackay (1994) noted the restricted range of methods accepted for mathematics tests at Key Stage 2 (age 7–10 years) of the English National Curriculum at that time.
Teachers should be aware of their own cognitive style. If they are towards the extreme ends of the continuum, then they will need to make a conscious effort to ensure they are communicating with learners from the other end of the spectrum. This mismatch of cognitive style between learner and teacher could be one of the reasons why students say, ‘I could understand algebra the way Mrs Jones explained it last year, but I can’t understand the way Mrs Smith explains it this year.’
Sometimes when we lecture for teachers we may ask them to try some questions which can identify their own cognitive style. It is interesting to note in that almost every group that we have done this with, internationally, there is no dominant style within the group, rather a close to even split between the two styles.
Sharma (1989) and Marolda and Davidson (2000) have noted that quantitative and qualitative personalities prefer different learning materials, distinguishing between discrete or quantitative materials (e.g. number lines, bead strings) and continuous or qualitative materials (e.g. Cuisenaire rods, empty number lines). This is just one of the factors teachers have to take into account when choosing concrete materials to illustrate a mathematics concept. Choosing appropriate materials is another teaching skill with, once again, a range of responses from the learners.
Summary
If you are to teach effectively and diagnostically then you must be aware of and respond to the nature, variety and consequences of the child’s strengths, weaknesses and cognitive style. An awareness that there is a range of cognitive styles in any teaching group can help the teacher present a lesson more effectively and to a broader spectrum of learners.
The inchworm needs to learn how to overview a problem before embarking on a procedure and how to appraise and evaluate an answer, preferably by using an alternative approach. He needs to move towards knowing ‘Why?’ The grasshopper needs to learn how to document his methods and how to focus on the detail as one way of checking the validity of his answers. He needs to move towards knowing ‘How?’ Krutetskii’s advice of harmonious use of both styles makes for good problem solvers.
