12
Operating with Fractions
Introduction
Work with simple fractions epitomises the assertion that, ‘Mathematics is easy, only writing it down is hard’. For example, as we shall show, it is very easy to make 3
+ 1
into 4
using the paper‐folding model advocated in this book for introducing fractions, but the written version, which carries with it a complex and thus difficult to explain algorithm, seems very difficult indeed by comparison. The work in this chapter is designed to link the ‘doing’ with the ‘writing down’ with the aim of making them equally easy. The paper‐folding model also provides a visual and kinaesthetic image to help the student recall and use the algorithm correctly.
As in Chapter 11, the ideas illustrated and validated by using paper folding show the student what the written version should be, so that the written version of the problem relates directly to the concrete and visual demonstrations. Thus, whenever the written problem proves to be difficult there will be a parallel paper‐folding procedure or visual image to support understanding and thus memory.
Here, as elsewhere in this book, the structure brought out by these models and procedures is intended to contribute towards the pupil’s overall understanding of the algorithms and concepts. The use of folded‐paper fractions is usually a clear enough method for understanding the examples and thus only a minimum amount of explanatory text is needed. As in other chapters, you must use your experience with your students to blend the work to suit each individual. We suggest that the basic structure is, however, best left intact.
Making Segment Sizes the Same
It will become apparent during the course of this chapter that if two or more fractions are to be compared, added, or subtracted, their segments must be the same size. In mathematical terminology, this is expressed as, ‘the denominators must be the same’. Generally, their segments will not be the same size, but there is a method of making them so, which is fully consistent with the philosophy of this book. It depends on the argument that, for segments to be made the same size, the same paper‐folding steps must be used for all the fractions involved. Each fraction must be given the folds it does not already share with the others. The folding can be real, drawn, imagined, or written, but the objective will be a situation where for all fractions the same folding steps have been used. The experience gained earlier, in actually making fractions, will be valuable here.
Examples
Consider the fractions 
(Figure 12.1a).
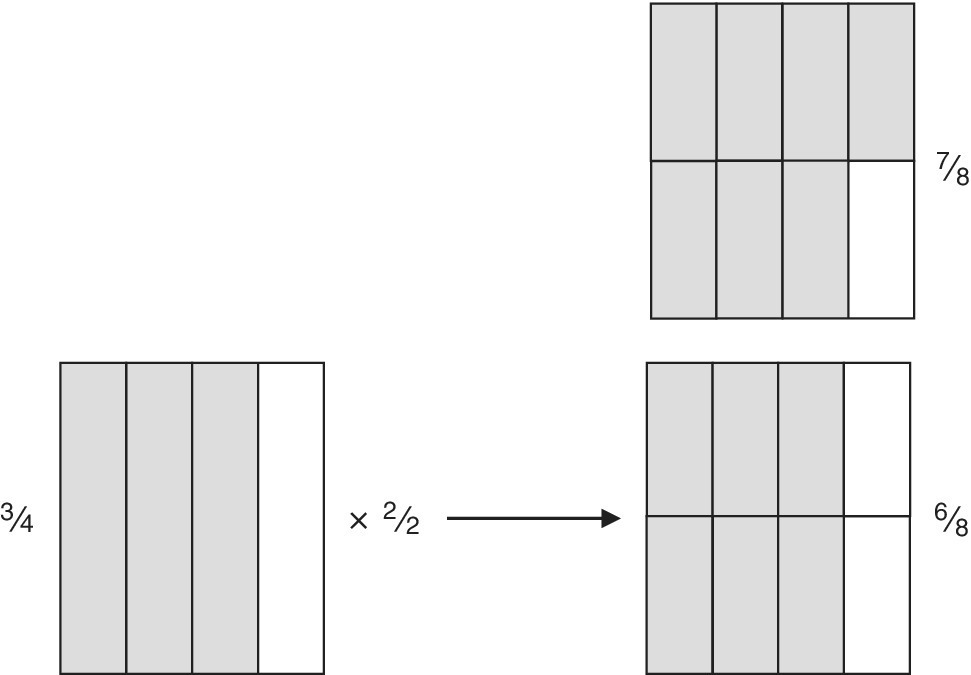
Figure 12.1a
¾ is changed to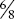 
, which can now be added to ⅞.
| The folding to make the fraction | Extra folding to create the same denominator (name) | |
| ⅞ | halved then halved then halved | none |
| ¾ | halved then halved | halved |
The written/symbols version is shown in Figure 12.1b. The folded‐paper diagram and the written version are now showing eighths as the segment size for both fractions.
Figure 12.1b Renaming one fraction to create the same denominator.
Consider the fractions and 
(Figure 12.2a). has been through halving and halving and has been through thirding. now needs thirding; now needs halving and halving.
Figure 12.2a Adding fractions with different denominators: ¾ + ⅔.
The written/symbols version that gives this outcome is shown in Figure 12.2b. Now the segment size for both fractions is twelfths. With this procedure it is unnecessary to know in advance that the shared segment size will be twelfths.
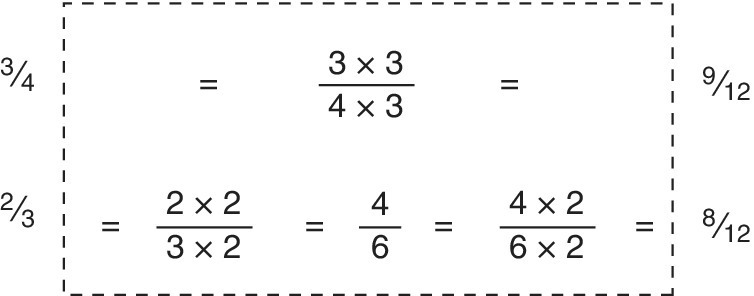
Figure 12.2b Renaming both fractions to create the same denominator.
Consider the fractions 
and 
. After analysing how they are formed:
| The folding to make the fraction | Extra folding to create the same denominator (name) | |
 |
halved then thirded | fifthed |
 |
halved then fifthed | thirded |
it is evident that now needs fifthing and needs thirding. Now by using the written form only, we have:
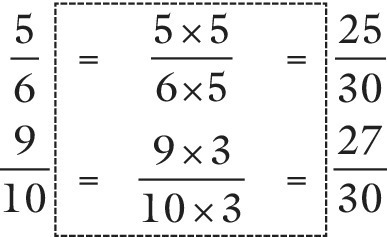
In later examples, where this calculation is done, the region of working will be highlighted within a dotted rectangle as it has been in these examples. Of course, this is not necessary beyond this book.
Comparing Fractions
Examples
Which fraction is bigger: 
or ?
Some students would say , because there are more segments, whereas others would say because the segments are bigger. Even a picture of the folded‐paper version leaves some doubt (Figure 12.3a).
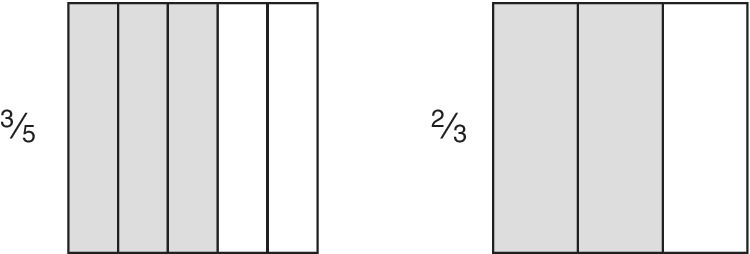
Figure 12.3a Comparing fraction values.
Fractions can be compared best when their segments are the same size. This can be achieved by the procedure detailed in the previous section, which involves further folding: real, drawn, imagined or written. Again, the objective is a situation where both fractions have been through the same folding procedure. has been through fifthing. has been through thirding.
Therefore, now needs thirding and needs fifthing (Figure 12.3b).
Figure 12.3b Adding fractions with different denominators: ⅗ + ⅔.
The written version of this would be as shown in Figure 12.3c. Both the folded and written versions show to be bigger (by 
).
Figure 12.3c Adding fractions with different denominators; written version.
Which fraction is bigger, 
or 
?
After considering how the paper would have been folded to make these fractions, it is evident that the needs to undergo another halving process. Using only the written form:
which makes bigger (by 
).
Converting mixed fractions to top‐heavy fractions
2 is called a mixed fraction, because it has a whole‐number part and a fraction part. It is frequently necessary to convert the mixed fraction into segments (in this case quarters). Figure 12.4 shows the paper and written/spoken versions. The result is known as a top‐heavy fraction for obvious reasons. The careful use of words in the written/spoken version is deliberate and necessary at first. This is because many students who have seen this work before remember incorrect methods. This will inhibit the learning of new methods for the same problems. They remember a rule that says something along the lines of, ‘Multiply something by something and add something’, but unfortunately mix up their somethings. Until they understand why they are multiplying and adding, they are likely to confuse the steps and write 2 × 1 + 4 (giving 5) or 4 × 1 + 2 (giving 6) rather than 2 × 4 + 1 (giving 9).
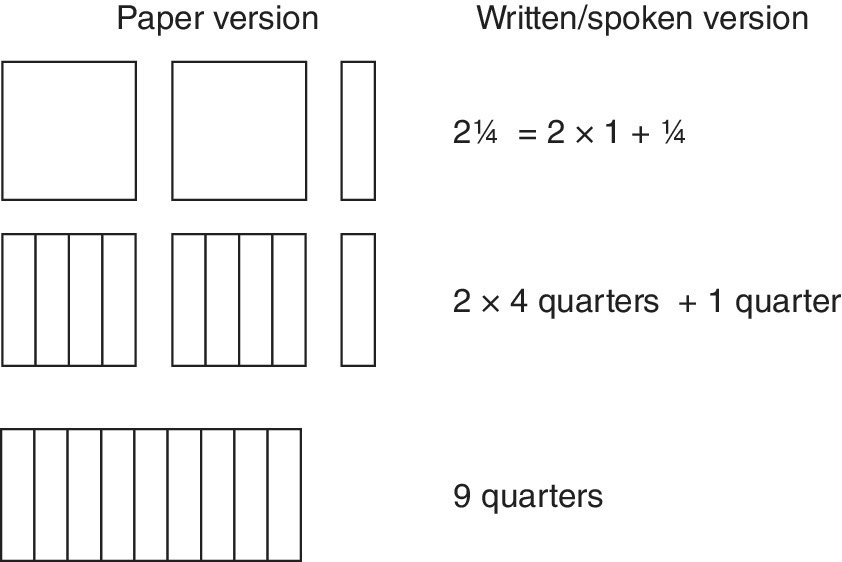
Figure 12.4 2 s a ‘top heavy’ fraction: 
.
Converting top‐heavy fractions to mixed fractions
Top‐heavy fractions are also called ‘improper’ fractions, a name that suggests it maybe undesirable to leave them in this form. They can be converted into mixed fractions as follows.
Example
As the segments are thirds, they must be grouped in threes to form whole numbers (Figure 12.5). Any remainders will stay as thirds. The essential working is a division by three:
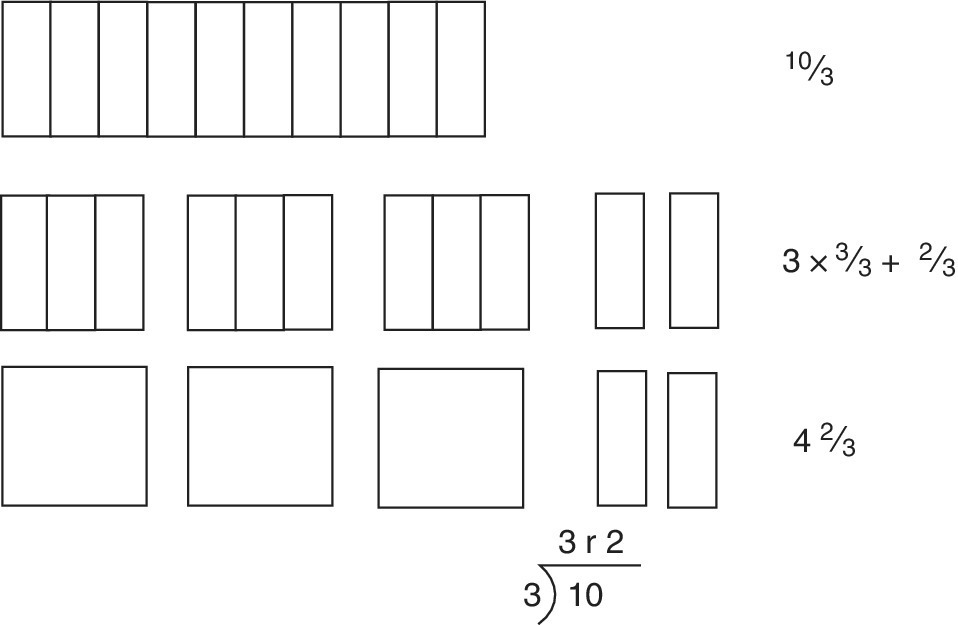
Figure 12.5 Converting 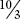to 3.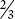
The results may be interpreted as follows:
Spoken version:
- ‘Ten thirds
- There are three lots of three thirds in ten thirds, with two thirds remaining.
- Three lots of three thirds make three ones.
- Two thirds left over makes 3 and ⅔.’
Written version =3 × +
=3 × 1 + =3
Combining Fractions
Caleb Gattengno (Brown et al., 1989) in his farewell address to the ATM in 1988 spoke of adding fractions:
Once at my desk in Addis Abbaba in 1957, I blushed. I was so ashamed of myself. 1957, twenty years after I got my doctorate in mathematics, I understood what we do when we add two fractions…I did not know that to add two fractions involves addition. I said it but I didn’t know it. I could write it, I could get the answer, but I didn’t know what it meant to add two fractions. And suddenly, I realised that, whenever I have pears and apples, two pears and three apples, I don’t have five apples or five pears. I have something altered, I have five pieces of fruit. So why did I do that? Because I wanted to find how to get them together, I had to raise myself to another level where pears, pearness and appleness are replaced by fruitness. And at that moment I can say five. And I never realised that ‘common denominator’ meant ‘give the same name’ to both. And in the middle of the word ‘denominator’ I see a French word ‘nom’ which I knew very well. It didn’t strike me, ever, that it is addition that forces me to get denominators, common denominators, not fractions. That was my shame…
There are so many messages in that paragraph, not least, that true understanding of a topic may come after many years of illusory success.
Vertical and horizontal presentations of fraction problems
We believe that a major cause of misunderstanding and confusion with fractions derives from the radical differences between the procedures used for addition and subtraction and those used for multiplication (and division). These differences are summarised in Table 12.1.
Table 12.1 Combining fractions using paper folding.
| Addition/subtraction | Multiplication |
| Addition and subtraction cannot take place until there are common denominators (i.e. equal segment sizes). | Multiplication can take place without common denominators. |
| The denominators are neither added nor subtracted. | The denominators (and numerators) are multiplied. |
| Simplification is done at the end. | Simplification is done as early as possible. |
| Whole numbers are treated separately. | Whole numbers are combined with fractions (to make mixed fractions). |
Paper folding is used as the (two‐dimensional) model to illustrate the combining of fractions. This demonstration can be shown to relate directly to the written algorithm. It simplifies each operation and provides a solution to the problem summarised in Table 12.1. It leads naturally to a vertical layout for addition and subtraction, which contrasts with the horizontal presentation suggested for multiplication. Further advantages of this will be discussed later in this chapter.
The difficult concept of division of and, especially, division by fractions is discussed later in the chapter. The ‘normal’ algorithms that are used to solve division problems for fractions must seem totally irrational and bizarre to many students (and adults). Some explanation is given, along with two methods, one vertical and the other horizontal.
Adding Fractions
This section starts with using paper folding to provide a concrete image of the operation. The explanation then moves to a more conceptual/symbolic level to extend the student’s performance and streamline his work. The initial descriptions progress from the easiest operation on fractions with the same denominator (segment size) to problems that involve mixed fractions.
Fractions where the segments (denominators) are the same size
Example
+ 
Paper, written and spoken versions are given in Figure 12.6. The reference to a ‘spoken version’ introduces another two senses, oral and aural, and emphasises that adding fifths to fifths produces fifths, that is, there is no change in segment size (or name), just as adding a number of marbles to another set of marbles still produces marbles. Thus, examples of this type are used to establish that segments must be the same size before addition can proceed. You can judge how many examples of this type are needed to establish this fundamental precept.
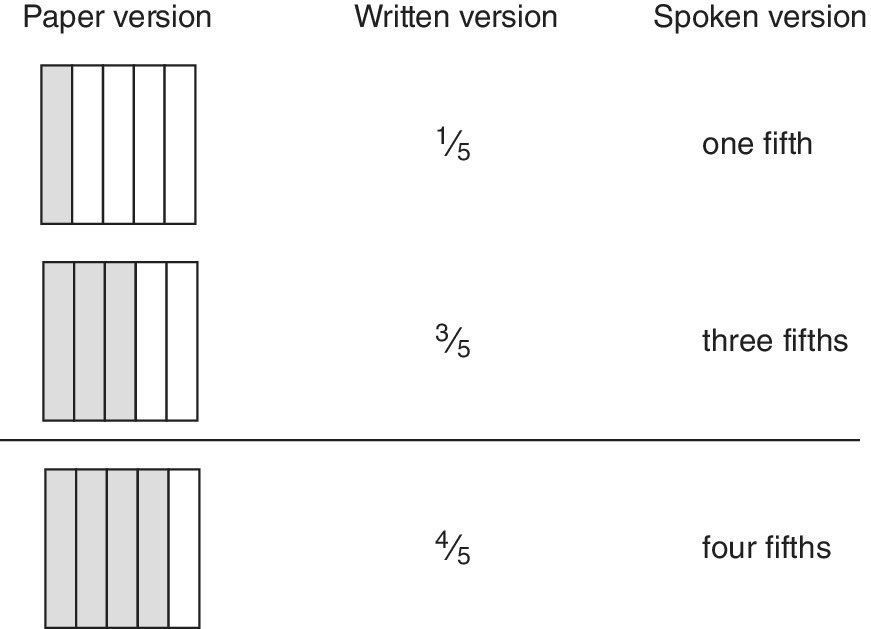
Figure 12.6 Adding fractions with the same denominator.
Adding fractions where the segments are of different size
Example
+
Again the different versions are given (see Figure 12.7). The paper‐folding version signals a problem since the segments of the two pieces of paper in this type of problem are of different sizes. The spoken version confirms that like is not being added to like. You could discuss this problem with the student, ‘What would be the segment size of the result?’ if such an addition were to proceed.
Figure 12.7 How do we add fractions with different denominators?
The student’s attention should be focused on the segments, which are not the same size (and do not have the same name). This is the reason addition cannot proceed without some modification to one or both of the segment names. The modification is to make the segments the same size (or give them the same name). So, the half is fifthed to make tenths and the fifths are halved to make tenths. In this example, the new segment size is tenths, because both halves and fifths can be modified to this segment size (see Chapter 11). Both existing segments can be folded again. The written version is given below:
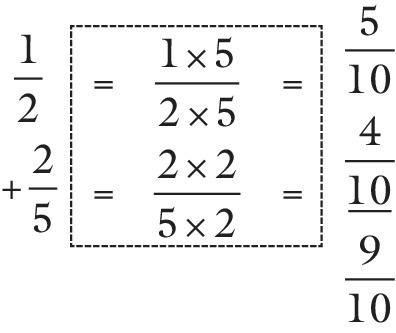
This follows the steps with the paper folding and extends the method described in Chapter 11, which made segments the same size.
Adding more than two fractions
The same method, of making segment sizes the same, can be extended. Again the principle is to obtain the same segments (names) for each fraction. Since more fractions are being added there is a likelihood of larger answers, possibly resulting in a top‐heavy fraction.
Example
+ 
+ 
The common segment size is twelfths (Figure 12.8).
Figure 12.8 Adding fractions resulting in a ‘top heavy’ fraction.
The written version is as follows:
Adding mixed fractions
Mixed fractions with segments that are the same size
The procedure is similar to the addition of simple fractions, but the student is learning to treat the whole numbers and fractions separately.
Example
2
+ 3
The folded‐paper version (Figure 12.9) shows the answer clearly and also relates well to the written version:
Figure 12.9 Adding mixed numbers: 2 
+ 3 
.
It demonstrates the need to deal separately with the whole numbers and the fractions in the same way that tens and units are dealt with separately in whole‐number addition.
Mixed fractions with different segment sizes
Once again, the student has to focus on the size of the segments and remember from the example above to deal with the whole numbers and fractions separately. Thus, the exercise can be used to reinforce previously learnt skills.
Example
21/4 + 12/3
The written version is:
It would be simple to use paper folding to demonstrate the above steps, confirming the algorithm and the answer:
Subtracting Fractions
The basic principle is the same as for addition. The student has to learn that the segments have to be the same size (same name) before subtraction can proceed. As with addition, a series of progressively more complex examples is given.
Fractions where the segments are the same size
Example
−
Paper, written, and spoken versions are given in Figure 12.10. The spoken version confirms that the segments are the same size (have the same name) for the subtraction process.
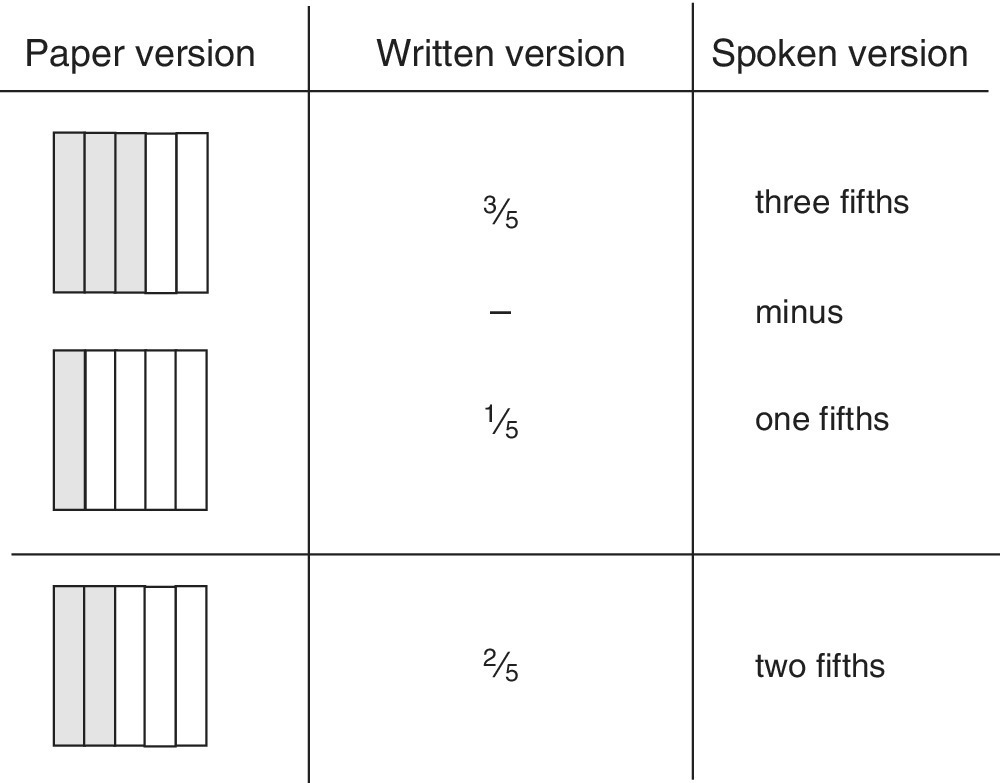
Figure 12.10 Subtracting fractions with the same denominator.
Fractions with different segment sizes
Example
− 
The paper version (Figure 12.11) shows that the problem is impossible to complete in this form (by showing different segment sizes). The spoken version confirms this because the segments have different names. The problem requires, as with addition, that the segments should be made the same size, in this case, fifteenths. Again, the concrete example of paper folding focuses on the critical part of the algorithm, the need to work with segments that are the same size:
Figure 12.11 How do we subtract fractions with different denominators?
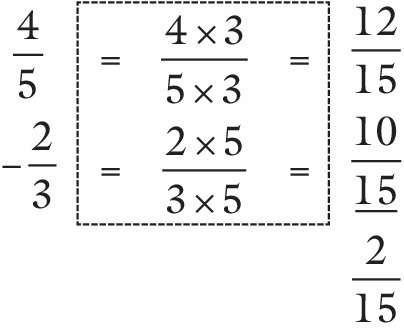
Subtracting mixed fractions
Mixed fractions where the segments are the same size
Example
3
− 2
The paper version is shown in Figure 12.12. The answer is clearly 1, and it is also clear that the whole numbers should be treated separately. The written version is as follows:
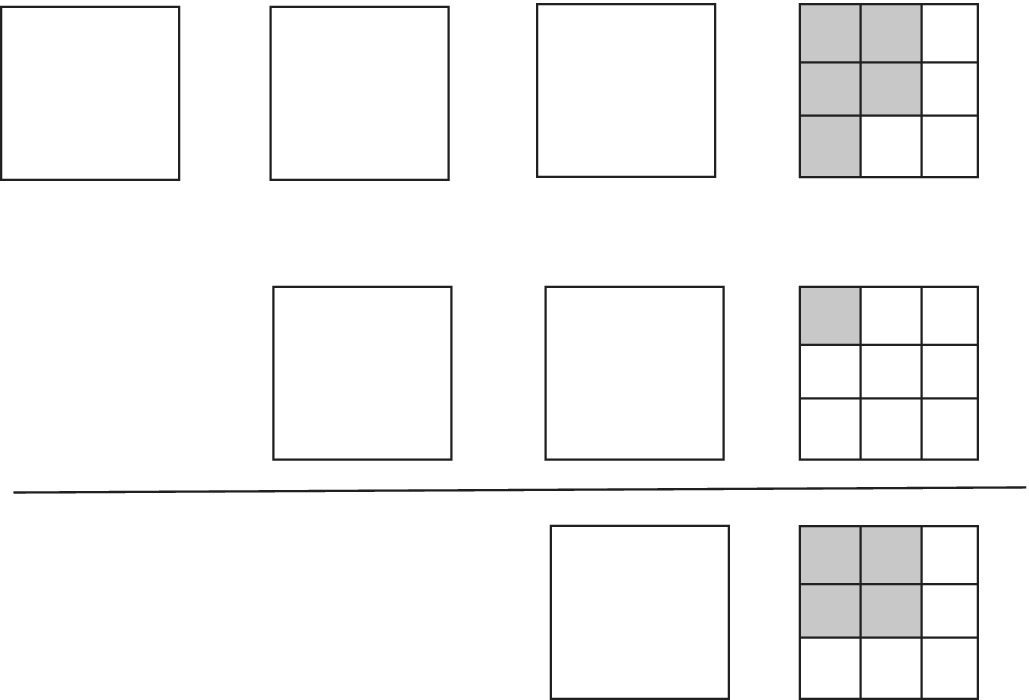
Figure 12.12 Subtracting mixed numbers: 3 + 2 .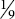
Mixed fractions with different segment sizes
Again, the student has to focus on the segment sizes. The segments must be adjusted to be the same size (and to have the same name) and the whole numbers and parts must be dealt with separately. The student can use paper folding for all parts or just the fraction part of this problem. For the convenience of brevity only the written version is shown for this example:
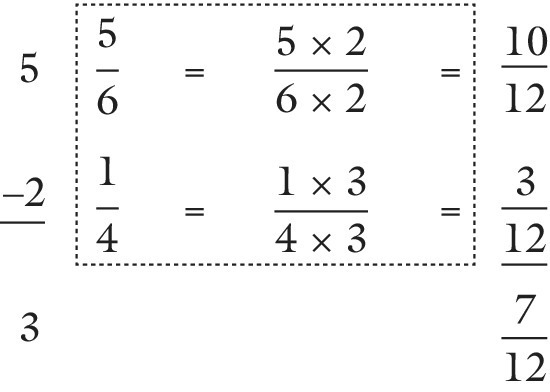
Mixed fractions where a bigger fraction part is subtracted from a smaller fraction part
Example
3
− 1
Since is bigger than , the problem requires an adjustment not dissimilar to a whole‐number subtraction such as 374 − 158, where 8 is bigger than 4. The solution to this difficulty with fractions is very similar to that used with whole numbers. The student has to use a whole number and convert it to a fraction in the same way as a student doing a whole‐number subtraction has to use the tens column to obtain ones.
Thus, the algorithm is not another new, unrelated idea to learn. You are showing the student the wide applicability of mathematical procedures. The action of paper folding provides a concrete model for the algorithm and a multisensory input to the memory. The paper‐folding procedure also confirms for the student that is bigger than . The paper version is given in Figure 12.13.
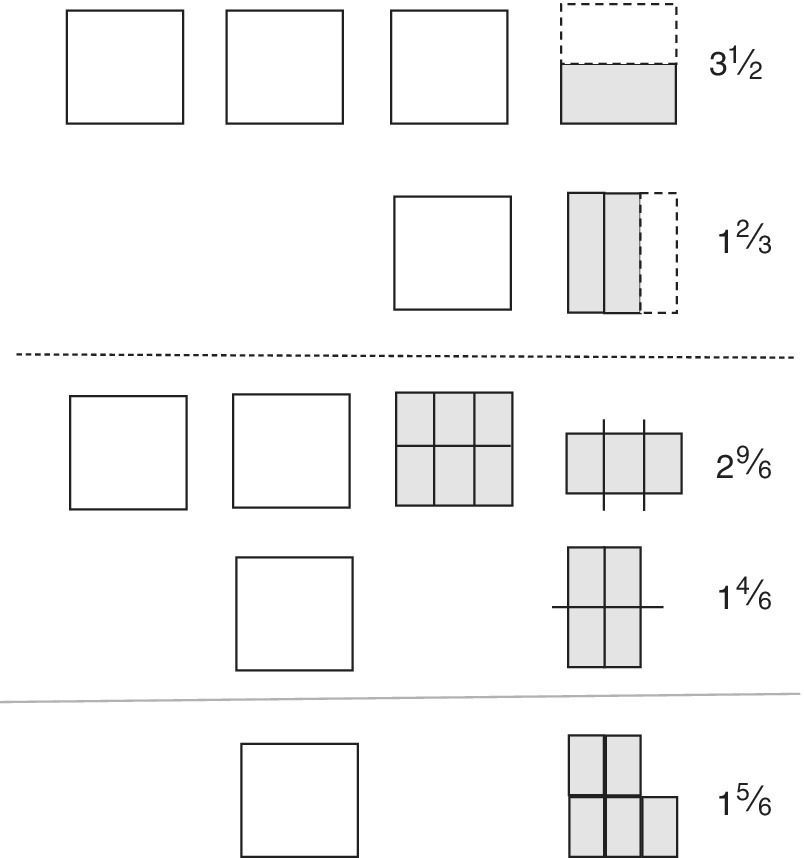
Figure 12.13 Subtracting mixed numbers where the fractions have different denominators.
The written version is as follows:
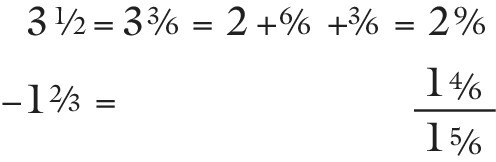
Combined Additions and Subtractions
Both addition and subtraction of fractions require:
- Segments of the same size (same name) and
- Whole numbers to be treated separately from parts.
Consequently, it is possible to perform both operations in the same calculation without a change of procedure. The student may need to use paper folding, but by now he may be able to move straight to the written algorithm.
Example
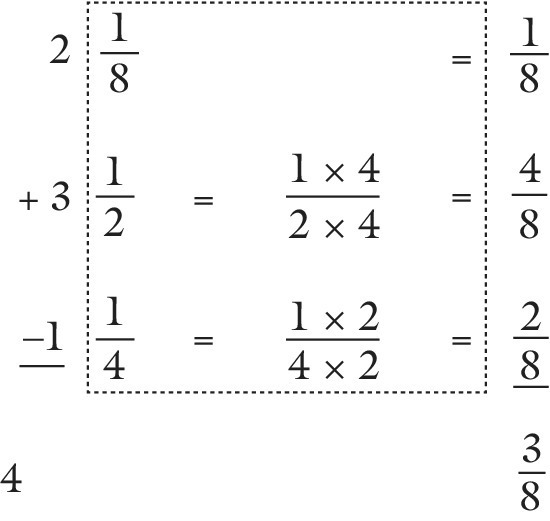
It may be advantageous to explain to the student why the addition and subtraction of fractions have been presented in a vertical format. The following summarises the advantages.
Advantages of the vertical layout for addition and subtraction of fractions
- It signals the need to make segment sizes the same.
- There is less likelihood of adding or subtracting the denominators.
- It allows room horizontally to change the segment sizes.
- It lines up fractions and whole numbers separately and encourages the student to deal with them separately.
- Numbers are added and subtracted vertically, which is a more familiar and easier method for most students.
Multiplying by Fractions
The language of multiplication should be established first. As with percentages, the word ‘of’ is frequently used to denote multiplication. For example of 8 means × 8. If the student needs to be convinced of this use, then refer back to whole‐number examples such as, ‘How many sweets are there in seven packets of ten?’ or, ‘If one pen costs 20p, how much do I pay for eight of them?’
The question, ‘Is the answer going to be bigger or smaller?’ is particularly useful when evaluating the answers for fraction questions.
Fraction times fraction
For multiplication of a whole number by a whole number (Chapter 8) area was used as a model. Area is a two‐dimensional model. The paper‐folding model for fraction times fraction does the same.
The method of finding the fraction of a square of paper was explained earlier. Multiplication repeats the process in a second dimension. So, one dimension represents a and the other dimension represents b in a × b.
Example 1
½ × ⅓
This multiplication is carried out by using a square of paper to find one‐half of one‐third of the square.
Figure 12.14 shows 
shaded. A vertical fold gives one‐half of this third. The part shaded twice is one‐half of one‐third. There are six segments in all, so one segment is 
.
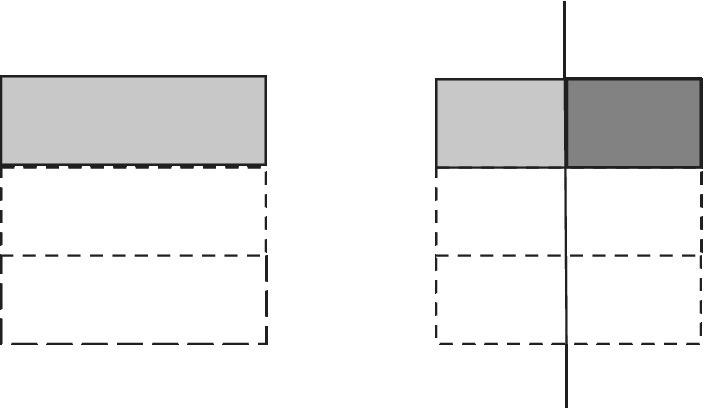
Figure 12.14 Multiplying fractions: ⅓ × ½.
The application of two fraction operations to the same square has two major implications:
- The change in segment size is seen to be inevitable. It should be obvious to the student that the answer will have a new segment size (and that it will be smaller).
- The horizontally written layout of this multiplication reflects the difference between this operation and its model to that used for addition and subtraction.
The written form of the example above is as follows:
Example 2
2/3 of
The square is folded into fifths in one direction and four of these fifths are shaded (Figure 12.15). The square is then folded into thirds in the opposite direction to give a grid with 
, shaded twice.
Figure 12.15 Multiplying fractions: ⅘ × ⅔ = .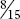
The concrete operation of folding and shading the square relates directly to the written form:
The student is multiplying the top and bottom parts of the fractions, which is easier to remember if the fractions are written side by side. The folding shows why three and five are multiplied together to make fifteen segments and why two and four are multiplied together to give eight of these segments.
Example 3
of
This results in an answer that can be simplified or reduced. The paper‐folding procedure is the same as in Example 2, leading to an answer of 
. Although this is not wrong, it would be more elegant to obtain 
.
The written version may be used to explain cancelling before and after the multiplication. This offers an opportunity to remind the student that fractions are about division and that a fraction may have more than one ‘name’.
Fraction times whole number
Example 1
¼ of 1 (Figure 12.16a)
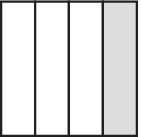
Figure 12.16a
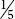× 1.
Example 2
¼ of 3 (Figure 12.16b)
Figure 12.16b
× 3.
The student should see that of 3 is three ‘times’, relating ‘times’ and ‘of’ once again. The written version relates exactly to fraction times fraction if 3 is written as 
:
Example 3
of 2 (Figure 12.16c)
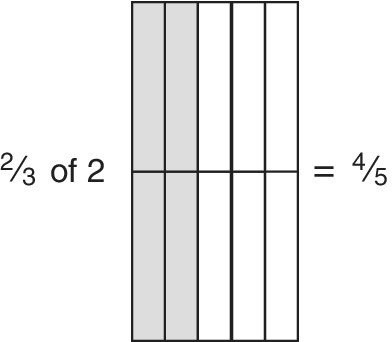
Figure 12.16c 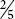× 2.
The written version is:
Multiplying Mixed Fractions
Example
3 × 2
The most probable error in this type of calculation arises when the student separates the fractions from the whole numbers, following an addition algorithm, and simply multiplies 3 × 2 and × .
A consistent application of the area model for multiplication shows the need for four separate multiplications (see Chapter 9).
3 × 2 gives four areas, A, B, C and D (Figure 12.17).
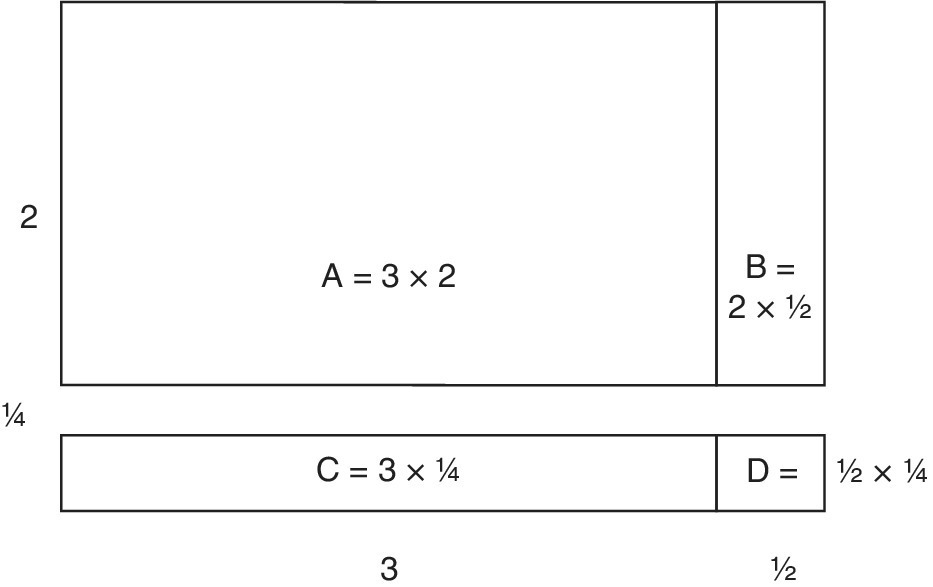
Figure 12.17 Multiplication using the area model.
This multiplication could be written as:
- A is 3 × 2 = 6 (which provides a simple estimate)
- B is 2 ×
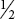= 1 - C is 3 ×
= 
= 
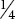- D is
× = 
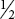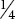- Total = 7
Although this provides a method consistent with that used for two‐digit times two‐digit whole‐number multiplications, it is more complex for fractions. So a procedure that is usually less open to errors is recommended. The mixed fractions are converted to top‐heavy fractions, which can then be multiplied together as for simple fractions:
A new diagram can be drawn to illustrate this written method (Figure 12.18). This rectangle shows there are halves (seven of them) and that there are fourths (nine of them). The unit square shows the answer will be in eighths and the 7 × 9 grid shows there are 63 of these eighths.
Figure 12.18 Multiplication using the area model.
With these larger numbers, cancellation may be done prior to multiplication in examples where this is possible.
Example
2
× 2
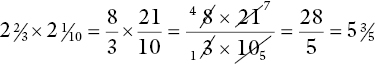
The advantages of a horizontal layout for multiplication
- It prompts the student to multiply in two steps: the top numbers first and then the denominators.
- It encourages simplifying by cancelling at the beginning.
- There is less temptation to treat whole numbers in isolation.
- It distinguishes between addition/subtraction and multiplication.
The advantages of different presentations for addition/subtraction and multiplication are best illustrated with an example that combines addition and multiplication.
Some students want to begin by an inappropriate separation of the portions of the problem. You should encourage the student to read the problem through and analyse its demands. The layout shown presents the problem clearly and logically.
The structured layout for the operations has extra advantages in this type of problem. It also follows the rules for the sequence of operations BODMAS (Brackets Order Divide Multiply Add Subtract), where multiplication precedes addition. Order refers to powers.
Example
Multiplying with fractions, an overview
This brief overview makes use of the question, ‘Is the answer smaller or bigger?’ In this case we also need, ‘Is the answer the same value?’
When we multiply a number by a fraction whose value is smaller than one, then the answer will be smaller than the number, but bigger than the fraction.
When we multiply a fraction that is smaller than one by another fraction that is smaller than one, then the answer will be smaller than either fraction.
When we multiply a fraction by one it stays the same value. This seemingly obvious statement is less obvious when renaming fractions, for example:
The outcome, 
does not look the same as 
, but it does have the same value.
Dividing with Fractions
A sequence of divisions may be used to introduce the student to this difficult concept (Ashcroft and Chinn, 1992):
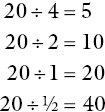
This may help the student to rephrase the question, a strategy that has quite extensive value. Thus, 20 ÷ can be re‐phrased as ‘How many halves are there in 20?’ A square of paper may be folded to make two halves, followed by the question ‘How many halves are there in one?’ It can be halved again, leading to the question ‘How many quarters are there in one?’ The process can be continued through 
, 
, 
to show the answer becoming bigger as the fraction becomes smaller.
Division by fractions
Two methods are described here. The first deals with simple examples and establishes a concrete image for this difficult concept. It is harder to explain the second method in this way, but it is an expedient way for those who progress to algebra.
The first method is set out vertically, whereas the second method is presented horizontally (it being more akin to multiplication).
Division by making the segments the same size
Example
÷ 
The spoken version of this problem needs flexibility for mathematical vocabulary again. It could be read as ‘seven‐tenths divided by one‐tenth’, but the student is more likely to understand, ‘How many one‐tenths are there in seven‐tenths?’ Again, the ability to rephrase a question can take the student a long way towards the answer of seven.
Example
÷ 
The use of the same spoken version leads to, ‘How many one eighths are there in three‐quarters?’ This makes about as much sense as, ‘How many cars are there in a pencil?’ However, the alternative interpretation: ‘Divide three‐quarters into eighths’ indicates more clearly that the segment sizes (denominators) should be made the same. So, that is the first step. Figure 12.19 shows the paper, written, and spoken versions.
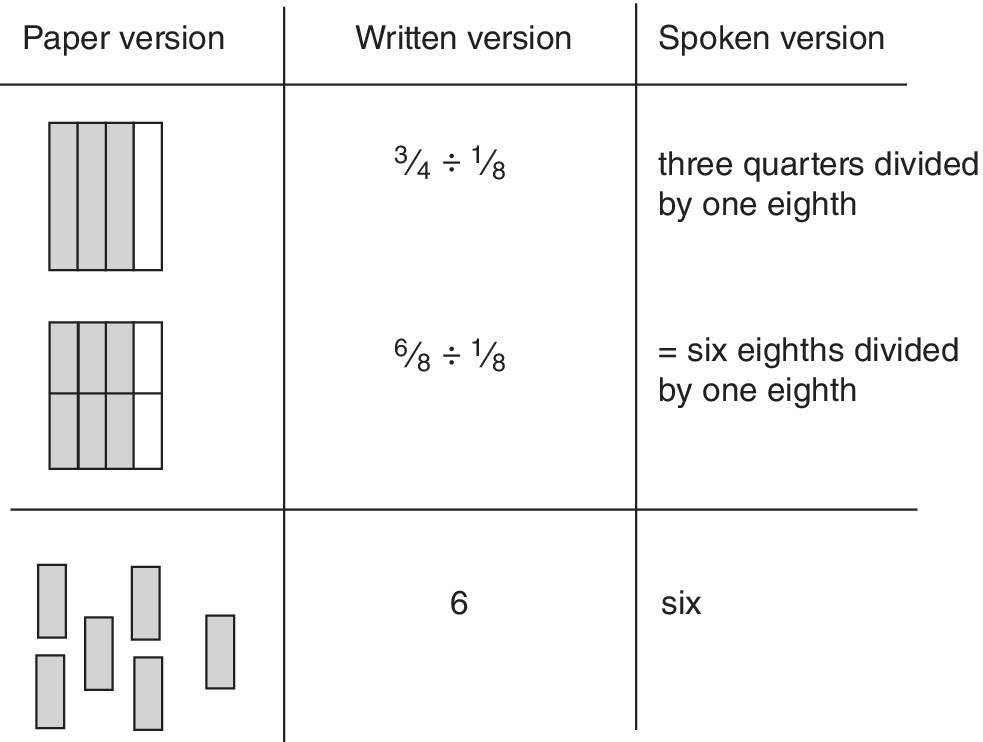
Figure 12.19 Dividing with fractions by changing denominators.
Example
÷
This is shown in the written version only:
Examples with mixed fractions
The initial step for the method advocated is to convert the mixed fraction into a top‐heavy fraction.
Example
3
÷
Since the segments are already the same, the division can be done immediately. The three versions are shown in Figure 12.20. The question is interpreted and illustrated as, ‘How many groups of three quarters are there in fifteen quarters?’
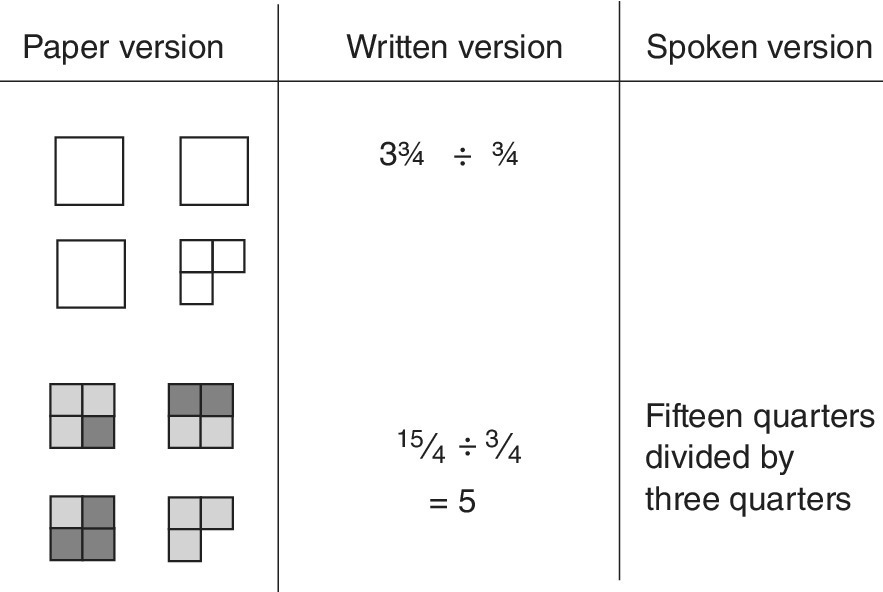
Figure 12.20 Comparing the visual, symbol and written versions of division with fractions.
Example
5 ÷ 2
This is shown in written version only, for the student who has a well‐established model of fractions:
Dividing fractions by inverse multiplication
This method is quicker, but requires the student to remember a seemingly inexplicable rule. So 4 ÷ is calculated as 4 × 
. In our experience this is one of the best recalled ‘rules’ of maths, even by adults who have long since left the maths classroom. Perhaps it is the seemingly bizarre instruction to ‘Turn upside down and multiply’ that makes it so. Some students will be happy enough to accept the explanation, or rationalisation, that since multiplication is the opposite of division then there is a need to do an opposite thing with the fraction, that is, to turn it upside down.
An explanation for the algorithm can be developed for the student by a series of paper‐folding exercises.
- 1 ÷
By definition, one whole number divided into thirds gives 3 (Figure 12.21a).
- 3 ÷
Figure 12.21a Whole numbers divided by a fraction.
Four whole numbers divided into thirds will give 3 × 3 = 9 (Figure 12.21b).
- 4 ÷
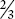
Figure 12.21b Whole numbers divided by a fraction.
Four divided into groups of two‐thirds will give (Figure 12.21c):
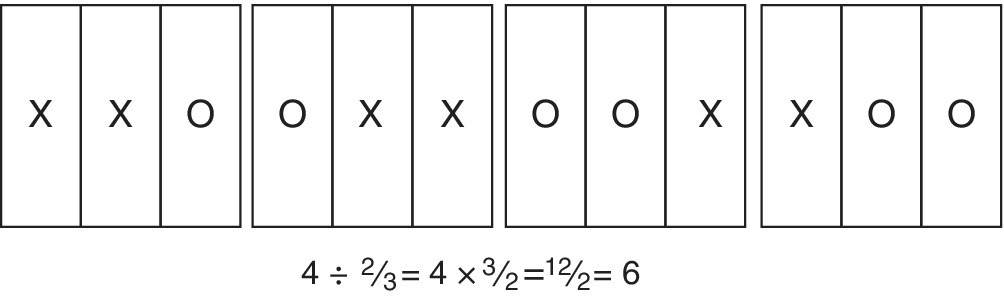
Figure 12.21c Whole numbers divided by a fraction.
Since 2/3 is twice as big as 1/3, the student should expect the answer to be half that of the previous example, that is, the previous answer has to be divided by two. However you choose to justify the rule, the pragmatics are that the fraction is inverted and then multiplied:
