13
Decimals
Introduction
Decimal numbers are an extension of the place value of our base ten system. They follow the same logic, but often the perceived inconsistencies block understanding. The processes of addition, subtraction, multiplication and division are identical to those covered for whole numbers in Chapters 8–10, but the decimal point confuses learners. This is not helped by books that suggest, for some calculations, ‘Move the decimal point.’
As with all chapters in this book, we will try to encourage an understanding of the work, partly by relating it to and building on previous concepts and knowledge.
Addition and Subtraction
Addition
Common errors tend to be due to misalignment of the decimal point, that is, incorrectly lining up the place values of the numbers involved (Ashlock, 2010). The tendency persists to line up the numbers from the right, irrespective of place value. Reinstating place value column headings can help.
An example of a common error pattern is:
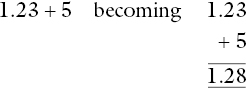
The correct process can be illustrated by using Dienes base ten blocks or similar apparatus. Effective help can also be provided with the use of money. For example, students who begin by adding £1.23 + £5 with coins will rarely try to add the 5 and the 3, as in the written version above. Reinforcement can be by using the suggestion that £5 may be written as £5.00, writing the .00 because it has no pence, and so the written version becomes:
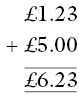
If written examples are linked with the student handling the equivalent money, then generally it becomes clear that pounds are added to pounds, pence are added to pence, and so on. The student can then be guided to write them under each other, a step which automatically puts the decimal points, which separate the pounds and pence, under each other. This gives the student a focus so that £0.09 + £0.5(0) is written as:
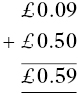
Coins provide the concrete memory hook for the student. The pragmatics are to use the decimal point as the marker of place value and to line up the numbers based on lining up the decimal points.
Another common error with decimal addition, 3.97 + 1.04 is shown below:

A student who makes this error has been content to carry a 1 from the hundredths to the tenths column, but has not carried a 1 from the tenths to the ones column, which requires him to cross over the decimal point. There is a lack of understanding here that the decimal columns are simply an extension of the whole‐number columns, that they are related in the same way, that is, increasing and decreasing in powers of ten and that they must follow the same rules. This problem was anticipated in Chapter 11, where the issue was clarified by the use of decimal number sequences. A demonstration with money can be used to provide further reinforcement. The example above can be viewed as £3.97 + £1.04 and written as:
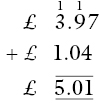
Thus 7 + 4 is 11 pence, which is changed (traded) for a single ten pence, carried to the ten‐pence column, and one penny which is retained as the answer in the one pence column. Similarly, in the ten pence column, the carried over one (a ten pence coin) is added to the nine and zero to give ten lots of ten pence. These can be traded for £1, which is carried into the pounds column.
Subtraction
Subtraction of decimal numbers presents students with virtually the same problems as addition. For example 24.38 − 0.6 might generate the error:

Here, the tendency, again, is to line up numbers from the right regardless of place value, compounded by the fact that 6 is easier to subtract from 8 than 3. The pragmatic solution to this problem is, as for addition, to use the decimal points as markers of place value and to line up the decimal points. Once again, a good manipulative material to illustrate and develop this procedure is coins.
Another common error pattern is illustrated by the example 48.5 − 2.36. This tends to generate two types of errors:
- Lining up from the right:

- Setting up correctly, but:

The 6 is just transferred to the answer line, before the rest of the calculation is completed correctly.
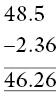
The use of an optional zero to ‘square off’ the calculation reminds the student that the 6 has to be subtracted, and gives him something to subtract from.

This can be practised with coins and place‐value columns.
Errors in the addition and subtraction of decimals can be reduced by reminding students of the ever‐present need to preview and review a question; to absorb some meaning and value for the numbers, and produce an estimate; and then check their answers against the estimate. This is likely to reduce the incidence of errors due to misalignment.
Multiplication and Division by Powers of Ten
Multiplication by ten
As with so much work in mathematics, place value is important here, so a review of the topic may be an advisable precursor to the next work.
Confronted by the question 4.62 × 10, if the student can remember that 4 × 10 = 40 then this can help him to see that 4.62 × 10 (as ‘4 and a bit’ times 10) should be forty‐something. Focusing on one digit from the number can reduce confusion and generate security. Alternatively, 4.62 × 10 can be interpreted as ten lots of 4.62 and can be evaluated the ‘long’ way (as a repeated addition):

Many students will notice that the digits 4, 6 and 2 have not changed, nor has their sequence in the number. This observation is, of course, an extension of the ten times table pattern. The digits have moved along one place value, so that each digit now represents a value that is ten times bigger. Most students can appreciate this pattern when it is pointed out to them. Base ten blocks or money can be used for manipulative work. The pattern and the procedure can be shown by considering each of the digits separately, using the base ten blocks or money.
As always, a multiplication is more efficient, quicker and less prone to error than the repeated addition of ten numbers.
When the calculation is written as 4.62 × 10 = 46.2, some students will imagine that the decimal point has moved rather than the digits. While this is mathematically incorrect, it is a simplification that is often the only way some students can remember what to do, especially if the computation is part of a longer calculation, when dual tasking can create problems. Actually, the digits move relative to the decimal point in order to have new place values. We would rather that this understanding preceded any pragmatic short cuts.
Multiplication by hundred
There are students who will be able to predict the effect of multiplying by hundred and they will conclude that the digits will move two place values.
As with multiplying by ten, an example that relates to known facts can provide an initial understanding of the operation, as well as a valuable estimation procedure (also useful when calculators are used). For example, if it is known that 2 × 100 = 200, then 2.375 × 100 (which is two and a bit times one hundred) should be expected to be two hundred and something. Then, if the digits and their sequence are not to change, then the two hundred and a bit must be 237.5. This result can alternatively be justified by treating × 100 as × 10 × 10 in two stages (compare with × 4 as × 2 × 2 in Chapter 7), and by using the same materials to demonstrate this.

Multiplication by thousand
At about this stage, students will usually see the pattern that the number of zeros in the (10n) multiplier dictates the number of places moved:
| Multiplying by ten | one place value |
| Multiplying by hundred | two place values |
| Multiplying by thousand | three place values |
For example, 27.1875 × 1000 = 27187.5. For justification, ×1000 is equivalent to × 10 × 10 × 10. Again a focus on a digit, say seven, which is seven ones, tells the student that it will become seven thousands. Again the other digits retain their sequence.
Multiplication by other powers of ten
The pattern can be extended, using similar arguments, illustrations and materials.
Division by ten
The initial goal is to show that division by ten is the opposite of multiplication by ten. The answer becomes ten times smaller rather than ten times bigger. The topic could be introduced using money or base ten blocks and the student asked to show coins or blocks that are ten times bigger or ten times smaller. The answers can be written on place value column cards.
For an example of the inverse relationship, 3p × 10 becomes 30p and conversely 30p ÷ 10 becomes 3p. The movement of the numbers is demonstrated by their place values on the card. A good demonstration of the required rule uses the argument that a division by ten and a multiplication by ten will cancel each other out, because they are opposites:
The second line above shows that division by ten causes a movement of one place, a movement which is in the direction opposite to that caused by a multiplication by ten.
Direction of movement
A decision about convention is now needed for describing the direction of a movement. Referring to the direction as left or right would be ambiguous, because if the digits move left, the decimal point moves right, and vice versa. Furthermore, terms such as left and right, forwards and backwards, in front and behind are all likely to confuse dyslexics, if they have laterality problems (Miles, 1983). We suggest that a safer and more meaningful practice is to describe the movement of the digits in accordance with whether the answer is bigger or smaller than the original number.
- Multiplication by powers of ten produces answers that are bigger than the original number.
- Division by powers of ten produces answers that are smaller than the original number.
This convention encourages overviews, estimates and reviews.
Division by hundred, thousand and other powers of ten
Divisions follow the same pattern as multiplications, in that the number of zeros in the divisor dictates the number of places moved, but now in a direction that produces smaller answers:
- Division by ten causes a movement of one place value
- Division by hundred causes a movement of two place value,
- Division by thousand causes a movement of three place values, and so on
This work can be justified, if necessary, by arranging divisions as repeated divisions by ten, or as reverse multiplications.
Examples
| 46.2 ÷ 10 = 4.62 | 40 becomes 4 |
| 346.5 ÷ 100 = 3.465 | 300 becomes 3 |
| 1872.3 ÷ 1000 = 1.8723 | 1000 becomes 1 |
| 985.3 ÷ 1000 = 0.9853 | 900 becomes 0.9 |
The last example illustrates inserting a leading zero and the need to explain this to a student. Again, there is the importance of using and appreciating place value.
Rationalisation (1)
It is worth anticipating student’s potential problems when trying to apply these procedures to whole numbers – only decimal numbers have been used so far in this chapter. Whole numbers do not display a decimal point, so three is written as 3 and not 3.0. Many calculators will change an entry of 3.0 to 3 as soon as an operation key is pressed. Students often tend to simplify the multiplication and division of whole numbers by powers of ten into a process of gaining or losing zeros. For example:
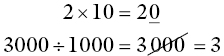
It is important that students do not see the treatment of whole numbers and decimals as two different processes. The two situations can be rationalised by again focusing on a digit:
Here there is a movement of one place value to make the answer bigger:
Here, there is a movement of three place values to make the answer smaller.
These procedures should rationalise all multiplications and divisions by powers of 10.
Multiplication of decimals by decimals
There is an expectation that multiplying a whole number will produce an answer that is bigger than the original number. Multiplying by powers of ten has been an example of this. However, for the example 0.6 × 0.8 this will not be the case (see Chapter 12 Summary). Often such outcomes are very difficult for students, still in the earlier stages of developing this concept, to understand unless they apply the procedure of focusing on a digit as well as recognising that 0.6 and 0.8 are smaller than 1.
The outcome can be first established using the area model (Figure 13.1) for multiplication, as in other chapters of this book. Within the unit square, divided into hundredths, as in the figure, the answer is shown by the area of the shaded rectangle. The small squares, each ![]() , show the answer to be
, show the answer to be ![]() or 0.48, which is less than either of the original numbers, 0.6(0) and 0.8(0). Of course, this is because the answer represents part of a part.
or 0.48, which is less than either of the original numbers, 0.6(0) and 0.8(0). Of course, this is because the answer represents part of a part.
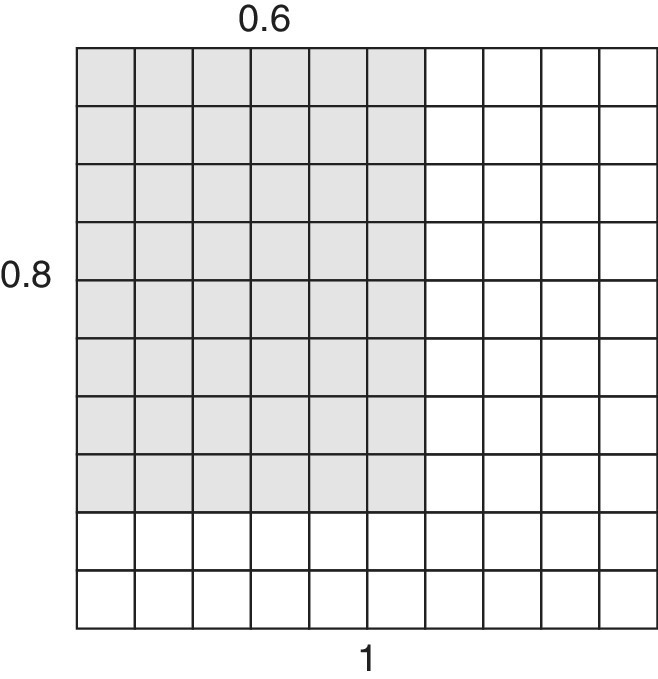
Figure 13.1 The area model for 0.6 × 0.8.
With or without the area model shown in Figure 13.1, the rule is best presented through fractions (Chapter 11 deliberately interrelated fractions, decimals and percentages), so 0.6 × 0.8 becomes:
In this example, the decimal places for 0.6 and 0.8 are treated as tenths. The tenths become, by multiplication, hundredths, so any rule for the decimal places must reflect this progression. A pragmatic rule for overviewing the process is:

The rule for the position of the decimal point can be stated as follows: ‘The number of decimal places in the answer is equal to the total number of decimal places in the numbers of the question’. The digits in the answer (48) are the result of multiplying together the numbers in the question (6 and 8), and are obtained independently of the decimal places. Therefore, the digits in the answer and the position of the decimal point are two separate considerations.
Examples

The final example shows that multiplication of a decimal by a whole number does not increase the number of decimal places. Quoting a special example such as this too early may lead to the over‐generalisation that the decimal points do line up. Taken with other examples, this can be shown to occur only when there is whole‐number multiplier.
Rationalisation (2)
In this chapter, it has been suggested that students are taught to expect a larger answer after multiplying by a power of ten or indeed any number greater than one, but to expect a smaller answer after multiplying by a decimal number with a value less than one. There is no ambiguity here, and the following explanation can be used to rationalise the situation, and also to encourage good estimations and checking strategies. A sequence such as the following is used:

The pivotal value of the multiplier is one, because any number times one remains unchanged in value. A multiplier bigger than one gives an answer bigger than the original number, whereas a multiplier less than one gives an answer less than the original number. This leads to the basic estimate/check procedure: ‘If the multiplier is bigger than one, expect the answer to be bigger, and if the multiplier is less than one, expect the answer to be smaller’. The overview is, once again, an important ingredient of the procedure.
An interesting sidetrack concerns students’ intuitive estimation of questions such as 0.4 × 0.002. Given that the choice of the answer may be:
- Bigger than 0.4,
- A middle value between 0.4 and 0.002, or
- Smaller than 0.002,
many students choose the middle value. A discussion as to the correct answer, with further examples, helps students understand the concept of multiplication by numbers less than one and acts as a useful reference/estimate for similar problems.
Division of Decimals
Division by a whole number
This work builds on the work of Chapter 10, with the added dimension of a decimal point, so a comparison with a whole‐number example is a good lead‐in. The traditional presentation for the problem 81 ÷ 3 is
A pre‐estimate of 81.6 ÷ 3 might be ‘less than 30, but more than 25’. The calculation could then be presented as:
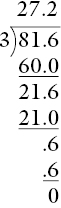
The result compares well with the pre‐estimate. For division by a whole number, the decimal points and place values line up with each other. The place value rules continue into the decimal digits. This algorithm sets the model for other decimal divisions.
Division by a decimal
A question such as 8.64 ÷ 2 follows the procedure above, because it is a division by a whole number. The question 8.64 ÷ 0.2 will often be set out (erroneously) in the same way, as follows:

Of course, division by 0.2 should produce a different answer to division by 2 and thus there will need to be a modification to the method for division by 2. It could be worth discussing why the answer is ten times bigger.
A rephrasing of the language of the question can help. Instead of ‘8.64 divided by 0.2’, the question can be understood as ‘How many 0.2 s are there in 8.64?’ or ‘How many £0.20s are there in £8.64?’ with the extra help of examining the value of 0.2(0) and of using money to set up the question. A pre‐estimate is then unlikely to suggest anything like four for the answer. As a lead into this argument, the student could ask ‘How many 0.2 s in 1?’ Since the answer is 5, the answer 4.32 cannot be correct.
For the written, exact version, a solution to the problem lies in modifying the question so that it becomes a division by a whole number. This can be explained using the procedure used for equivalent fractions: 8.64 ÷ 0.2 may be written as:
Multiplying the top and bottom of the fraction alters the division to 86.4 ÷ 2, without changing the final result (as in renaming fractions).
The division can then proceed as in earlier whole number examples:

Further examples
- 0.695 ÷ 0.05 becomes 69.5 ÷ 5 (moving the digits in both numbers two place values by multiplying both by hundred). The traditional algorithm follows:
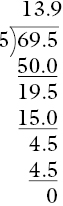
- 13.2 ÷ 0.006 becomes 13200 ÷ 6 (multiplying both numbers by a thousand and thus moving the digits in both numbers three places).
- 0.13 ÷ 0.8 becomes 1.3 ÷ 8 (moving the digits in both numbers one place value).

Note that in the final example 1.3 was written as 1.3000. The extra zeros are optional (see Chapter 11) and do not affect the value, but do help with the setting out of the question and lining up the digits in the correct places.
Approximations/rounding
Sometimes it is desirable to give an approximate answer in round figures. For example, £8.28 might be described as ‘nearly £8.30(£8.3)’, or ‘about £8’.
- For rounding to one decimal place (tenths) view 8.28 as being between 8.20 and 8.30. It is nearer to 8.30, because it is above the halfway position of 8.25. Therefore, rounded to 1 decimal place, 8.28 would be written as 8.3.
- For rounding to the nearest whole number, an analysis of 8.28 shows that it lies somewhere between 8 and 9. It is nearer to 8, because it is below the halfway position of 8.50. Therefore, rounded to the nearest whole number, 8.28 would be written as 8.
- A number line (Figure 13.2) shows quite clearly which approximation is nearer.

Figure 13.2 Using a number line to round decimal numbers.
A numerical policy is more readily applicable, however. The accepted policy is demonstrated in Table 13.1 through rounding a complete set of numbers to 1 decimal place (nearest tenth). The place to be retained is separated by a line from the place to be removed.
Table 13.1 Rounding decimal numbers.
| Nearer to | Rounded to | ||
| .60 = .6 | 0 | .60* | .6 |
| .61 = .6 | 1 | .60 | .6 |
| .62 = .6 | 2 | .60 | .6 |
| .63 = .6 | 3 | .60 | .6 |
| .64 = .6 | 4 | .60 | .6 |
| .65 = .6 | 5 | .70* | .7 by convention |
| .66 = .6 | 6 | .70 | .7 |
| .67 = .6 | 7 | .70 | .7 |
| .68 = .6 | 8 | .70 | .7 |
| .69 = .6 | 9 | .70 | .7 |
- When the place to be removed contains a five or more, the number retained is rounded up. This is a convention and thus a rule.
- When the place to be removed contains a four or less, the number retained is rounded down 0.
This is the policy that is normally applied, because it is even‐handed: half of the numbers are rounded up and half are rounded down.
Sometimes a division will produce an answer that is too long, and will have to be shortened, by rounding off excess/unnecessary places. Indeed, some divisions, such as 39.5 ÷ 7 would carry on forever. The early part of this calculation is shown:
The answer to this division is now given in various approximations:
- 6 to the nearest whole number, because a 6 creates a rounding up
- 5.6 to 1 decimal place, because a 4 creates a rounding down
- 5.64 to 2 decimal places, because a 2 creates a rounding down
- 5.643 to 3 decimal places, because an 8 creates a rounding up
Some decimals are particularly awkward to round. For example, approximating 9.999 to two decimal places. When rounding off the 9 in the second decimal place, then it is affected by the 9 in the third decimal place. This dictates that the 9 in the second decimal place, the hundredths now becomes ten hundredths, one tenth.
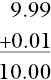
The act of rounding up has a knock‐on effect for the other digits. The two zeros after the decimal point must be retained even though they are normally regarded as optional. They are needed here to show the approximation to the required number of decimal places.
Rounding must be performed in a single step, for accuracy. Rounding in stages can produce errors. For example:
- 6.247 becomes 6.2 correct to 1 decimal place
But, using stages:
- 6.247 becomes 6.25 to 2 decimal places and then
- 6.25 becomes 6.3 to one decimal place, which is incorrect.
Converting harder fractions to decimals
In this chapter, it is possible to cover the types of example like ![]() , which were beyond the scope of the methods used in Chapter 11. The diagrams in Figure 13.3 are intended to show that
, which were beyond the scope of the methods used in Chapter 11. The diagrams in Figure 13.3 are intended to show that ![]() is the same as 5 ÷ 9.
is the same as 5 ÷ 9.

Figure 13.3 Converting fractions to decimals.
The conversion of ![]() to a decimal can now be achieved by calculating 5 ÷ 9 as a decimal division, and rounding the answer to, say, three decimal places. It will be necessary to work out four decimal places, so that the size of the fourth decimal place, and its consequent effect on the third decimal place, can be determined.
to a decimal can now be achieved by calculating 5 ÷ 9 as a decimal division, and rounding the answer to, say, three decimal places. It will be necessary to work out four decimal places, so that the size of the fourth decimal place, and its consequent effect on the third decimal place, can be determined.
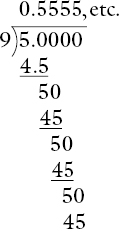

This method of conversion works for any fraction, even the earlier easy examples. Furthermore, in Chapter 11, it was seen that the conversion of ⅞ to a decimal requires some special knowledge. Now it can be carried out mechanically as 7 ÷ 8.
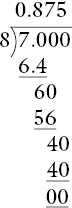
Of course, such divisions can be carried out using by calculators, with the ever‐present caveat, that the student can find an approximate answer beforehand.
Summary
In this chapter we have tried to explain and rationalise the methods used. We have also given some pragmatic rules to remember. Our hope is that the underlying understanding supports the memory for the rules.
- For addition or subtraction, all the decimal points of the question and the answer line up vertically.
- Modify the numbers in a division by making the divisor a whole number. This is achieved by multiplying both numbers by the same appropriate power of ten.
- The decimal points in a multiplication do not line up. The number of decimal places in the answer is given by the total number of decimal places from the numbers in the question. Then the actual numbers can be multiplied together in the normal way.
- Multiplication and division of decimals by ten, hundred, thousand, and so on, never changes the digits, nor their sequence – they merely move them to new place values. The number of places moved is dictated by the power of the ten used, whereas the direction of movement gives a bigger answer for multiplication, and a smaller answer for division.
Because addition, subtraction and multiplication ultimately follow the same rule, some teachers prefer to teach them first, in the given order. Division, often perceived as the odd one out, is then dealt with last.
Finally, and leaving out much of the detail, the policy for approximating when rounding is summarised by the following:
- Five or more means round up.
- Four or less means round down.
