9
Multiplication
Introduction
This topic will be used to illustrate the use of a full programme of instruction. The principles of this structure are applicable to other topics. The work moves from a manipulative aid, which is a direct representation of the problem, to a visual model (in this case, area), to purely written symbols and an algorithm which links back to the concrete model. Whenever possible the structure acknowledges different cognitive styles. The multisensory introduction is used to encourage flexible cognitive processes and to provide an overview.
There are some other methods that are used by some teachers and thus by some children. These include the Napier’s Bones method. An overview of the data from the standardisation of Chinn’s 15‐minute test (Chinn, 2017a) suggests that this method is often only partially remembered. The method makes for an interesting exercise for teachers, that is, to analyse all the prerequisite skills a student needs to make a particular method work, for example here, from spatial organisation to retrieval of basic facts. A failure in even one of the steps will result in a wrong answer. It is hard for a student to understand this method and thus hard to support memory without that understanding. It is also of note from the standardising data that the success rate for a three‐digit times three‐digit example (541 × 203) in this test was very low, with 15.2% of the 13‐year‐old cohort and 38.2% of the 15‐year‐old cohort achieving correct answers.
The key concepts
Learners need to know and understand that multiplication is about repeated addition of the same number. They also need to understand the role of place value, especially when multiplying by powers of ten.
Multiplying by Ten and Powers of Ten
This procedure is also needed to underpin estimation skills. Estimation skills in multiplication as used, for example, to back up calculator work, centre on an ability to multiply by tens, hundreds, thousands, etc. In our experience this relatively basic skill needs frequent review. It is a skill that depends on an understanding of place value.
The pattern for multiplying by ten must be explained in terms of the basic concept and the implication on place value, rather than solely in terms of the purely mechanical action of ‘adding on zeros’ or ‘moving the decimal point’, procedures which generate horror in the minds of many mathematicians, yet are readily adopted by children, who tend to act pragmatically, and are illustrated in some textbooks.
The objective is to explain that multiplying by 10, 100, 1000, and so on, moves numbers up in place value, but that the digits themselves do not change their sequence. To illustrate this, consider 536 × 10.
- 6 × 10. Use a place value card and put six ones cubes in the ones column. Remind the child of the ten times table and the exchanging of tens blocks for ones cubes. Then ask the child to exchange each ones cube for a tens block, placing the tens blocks in the tens column. Give the child a sheet of paper with place value columns on it and ask him to write in numerals the 6 and the 60. Discuss the 60 being ten times bigger than the 6 and emphasise that the 6 has moved to a higher place value, that is, from the ones column to the tens column and that this requires writing a zero in the ones column (Figure 9.1a).
- 30 × 10. Repeat the process, but exchange three tens blocks in the tens column for three hundreds blocks (squares) in the hundreds column (Figure 9.1b).
- 200 × 10. Repeat the process again exchanging two hundreds squares for two thousands blocks (Figure 9.1c).
- 236 × 10. Repeat the process all in one example (Figure 9.2). Then discuss what has happened to each digit, the relevance numerically, the pattern, what has changed and what has not changed in the process. The procedure can be illustrated with place value number arrows (Figure 9.3) as a further reinforcement of the concept.

Figure 9.1a Multiplying by 10. 6 × 10 = 60.
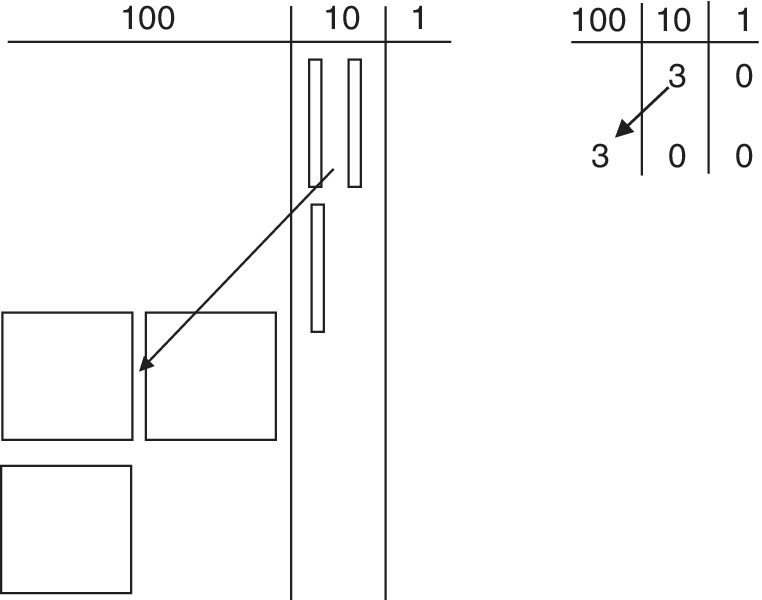
Figure 9.1b Multiplying by 10. 30 × 10 = 300.
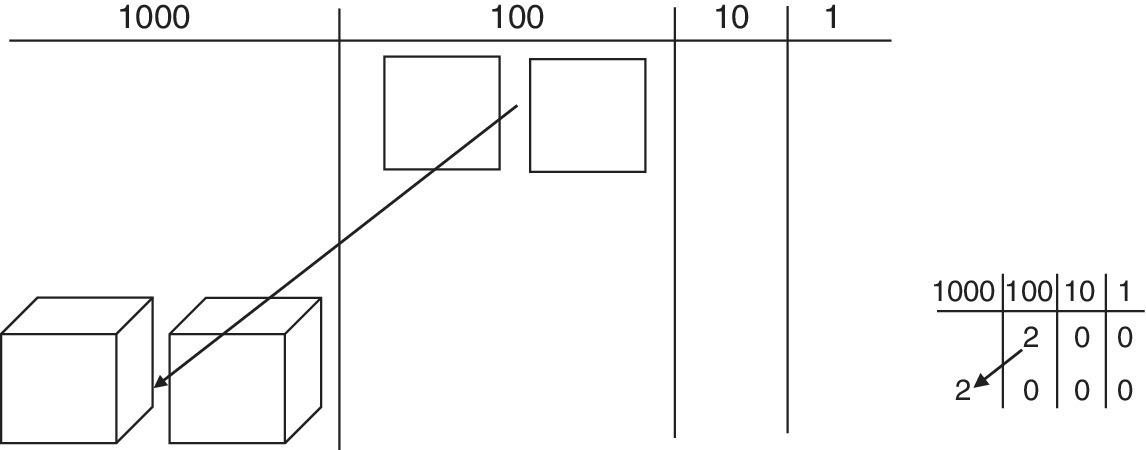
Figure 9.1c Multiplying by 10. 200 × 10 = 2000.

Figure 9.2 Multiplying by 10. 236 × 10 = 2360.
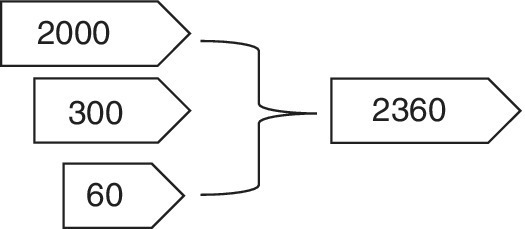
Figure 9.3 2360 = 2000 + 300 + 60
It should now be possible for the child to explain other calculations such as 849 × 10 = 8490, including the significance of the zero in the ones column, and to restate that the order of digits remains the same. As ever, this work includes a significant element of revisiting previous work and ideas.
A similar process can be used to teach × 100 and × 1000 and other powers of ten. One way of checking the answer is to focus on just one digit, for example in 849 × 100, focus on nine, which will be changed from nine ones to nine hundreds and the remaining digits follow in sequence:
The child should practise the work, using the base ten blocks for some examples, place value columns and (squared) paper for others. He should be encouraged to articulate his work and to review the underlying significance of the procedure.
It may be useful to extend multiplication by powers of ten to examples such as × 20, ×50, ×200 and so on. The method advocated is a two‐stage process, so that × 20 is done as × 2 then × 10 (or × 10 then × 2). The child should compare the results of × 2 with × 20 by using base ten blocks, for example 21 × 20:

giving:
The child needs to realise that, if the multiplier is ten times bigger, then the result of the multiplication is ten times bigger. This two‐step procedure is, of course, similar to the times table strategy of using × 2 twice for × 4.

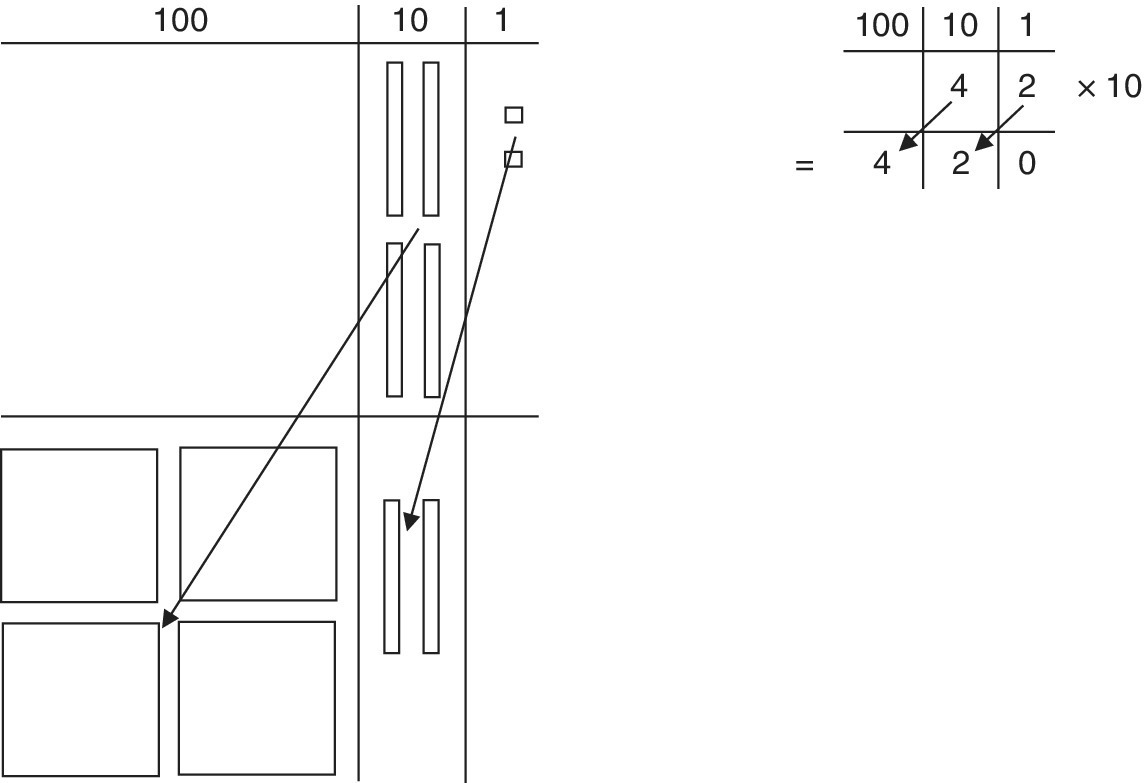
Multiplication
Times table facts are predominantly one‐digit times one‐digit operations, but also include × 10. This chapter extends this progressively to two digit times one digit and then to two digit times two digit and thus, by using the same models, to any multiplication. The model of multiplication used is area. This model is advocated because it can be extended into other aspects of multiplication, such as a fraction times a fraction and algebra.
Introducing the model
The child needs some square counters (Figure 9.5). The three piles illustrate three lots of four. This can be discussed as repeated addition, 4 + 4 + 4 leading to the more economical representation 3 × 4. The counters are then rearranged to represent area.
Figure 9.5 Square counters used to show 3 × 4 as three piles of 4 and as area 3 × 4.
The concept of a × b, that is, ab, as area can be discussed in real‐life terms, such as floor tiles, areas of walls for painting, etc.
Two‐digit numbers times one‐digit numbers
Consider the example 23 × 4. The child is going to learn a two‐stage procedure. This procedure was used in the times table chapter (Chapter 7), for example, where 7 × 6 was treated as (5 × 6) + (2 × 6), a process of breaking down followed by building up again.
Set up the multiplication with base ten blocks (Figure 9.6a). The area divides up into two sub‐areas. One area is made up from tens blocks and the other area from ones blocks. The two areas can be physically separated to show 20 × 4 (Figure 9.6b) and 3 × 4 (Figure 9.6c). The two areas can then be brought back together to show 23 × 4 (Figure 9.6a).

Figure 9.6 Base ten blocks to show the breakdown of 23 × 4.
At each step the written symbols are shown to the child. The demonstration shows and separates the two partial products. The child should set up some areas for himself and show the partial products both as blocks and as written digits.
Two digit times two digit
The model is again area. Consider the example 22 × 31. The inefficiency of repeated addition could be reviewed for this example:
Indeed, this overwhelming presentation would suggest some grouping, or chunking, which could be another route into the area model and the final algorithm.
- Set up the multiplication in base ten blocks (Figure 9.7a). The blocks illustrate area. They are movable, so that the four sub‐areas can be separated (Figure 9.7b). These partial products allow a difficult problem to be broken down into smaller, easier steps. The child can handle the blocks and physically break down the problem with the blocks, as well as with the written digits.
- The four constituent areas are discussed, starting with the largest area, the area formed by the ‘hundred squares’. This offers a first estimate. The blocks provide a very real model of this (Figure 9.7c). The estimation sum is written by the child in digits (30 × 20 = 600).
- The four areas are examined (Figure 9.8). They are: 30 × 20 1 × 20 30 × 2 1 × 2
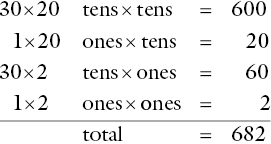
This algorithm is (a + b)(c + d) = ac + ad + bc + bd.
The child needs to see and handle each partial product in order to see that the area does break down into constituent parts. Each partial product should be written down in digits.
- The problem is drawn to scale on squared paper by the child. This will look like Figure 9.8b. The sub‐divisions are drawn in, and the relationship between the areas and the numbers in the partial products is explained.
- A problem is presented as numbers, for example 22 × 31. The partial products are written down and calculated. The child is asked to identify the ‘estimate’ partial product.
- The problem is drawn to scale again on squared paper and only one sub‐division is made, leaving two areas (Figure 9.9). In numbers the two areas are 20 × 31 and 2 × 31. The algorithm is based on (a + b)c = ac + bc.

Figure 9.7 Base ten blocks to show 22 × 31.
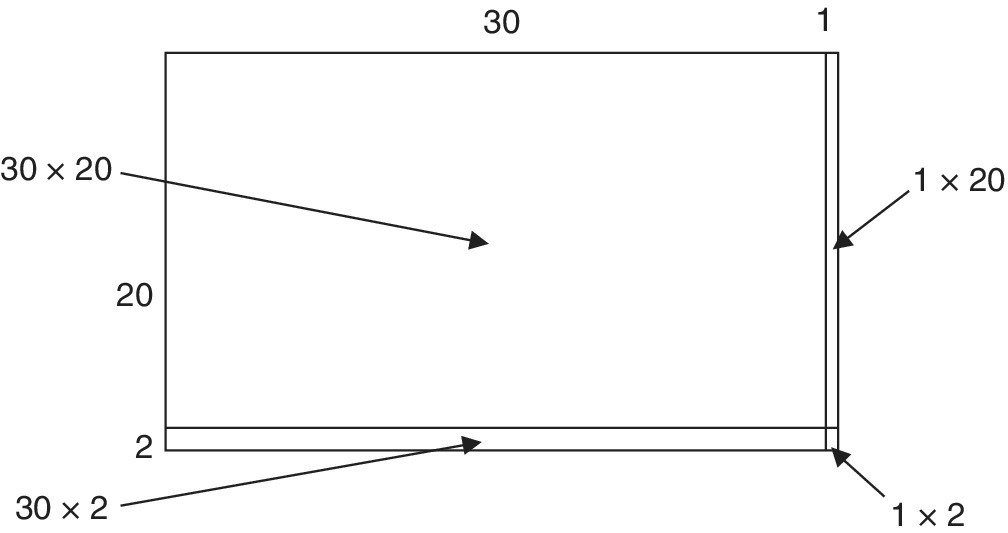
Figure 9.8 An area model for 22 × 31 as four partial products.
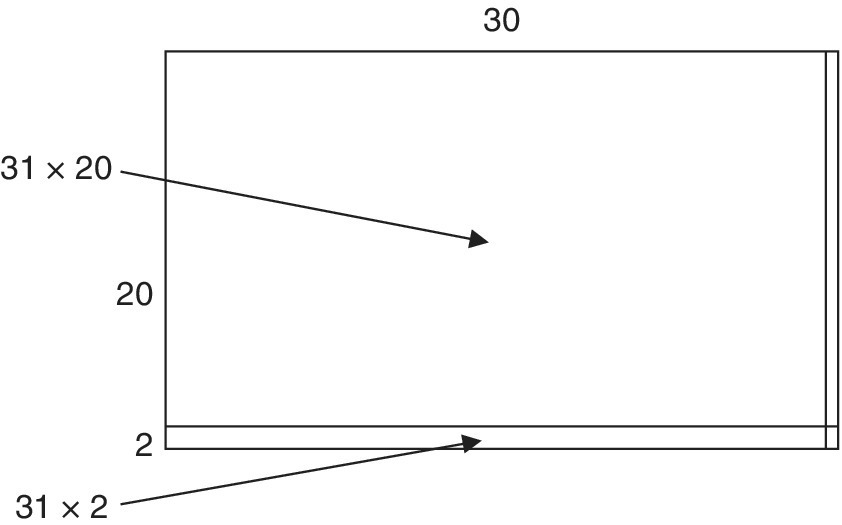
Figure 9.9 An area model for 22 × 31 as two partial products.
The calculation becomes:
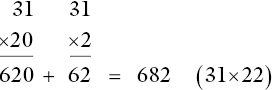
The child is still doing four multiplications as before, but he is combining two on each line of the calculation.
Compare the two methods as used for another example, 54 × 23:

There is a procedure, still using partial products, but as with the times table facts, using the core numbers to create the partial products. For example 247 × 77.
Seventy‐seven breaks down into 50 + 20 + 5 + 2 for the partial products. In this example, ×5 and × 50 are connected as are × 2 and × 20. Thus place value can be used to check the products.
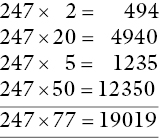
Einstein is purported to have said, ‘Everything can be made as simple as possible, but not simpler than that.’ This method restricts multiplications to the core facts. The interrelationships help with place value. However, there are now more partial products and thus more to add.
The same approach as used above will be adopted for division, where the additions of the partial products are replaced by subtractions.
The child should chose the method which best helps his particular strengths and weaknesses, for example organisation of work on the page, knowledge of basic facts and knowledge of place value.
Mnemonics
Mnemonics may help the child with a two‐digit times two‐digit computation. These will be used again for algebra expressions of the type, (x + a)(y + b). It is hoped that these will only be used once understanding is embedded and not as a substitute for comprehension.
FOIL (Figure 9.10)
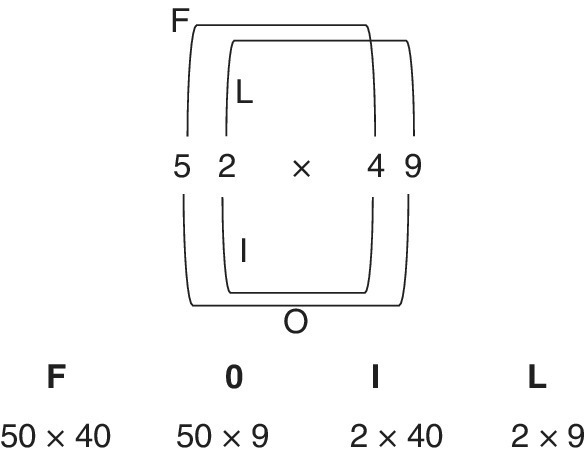
Figure 9.10 The FOIL acronym.
The First two digits are multiplied together: 50 × 40.
The Outer two digits are multiplied together: 50 × 3.
The Inner two digits are multiplied together: 2 × 40.
The Last two digits are multiplied together: 2 × 3.
There can, however, be place value problems with this mnemonic.
To reiterate, this ‘trick’ is merely a mnemonic and is not developing any understanding of the algebra involved. However, a limited use of mnemonics may be a survival skill for some students.
Estimation
Whilst calculators provide a relatively stress‐free way of multiplying, dyslexics and dyscalculics have a tendency to press the wrong number keys, get the numbers in the wrong order, use the wrong operation key or use the right operation key at the wrong time. A pre‐calculation estimate and a post‐calculation evaluation/appraisal are, therefore, important.
The area model provides a good picture of how to estimate, based on the biggest sub‐area, plus or minus the other sub‐areas. It also allows the child to evaluate his estimate and see if it is high, low or fairly accurate. Some examples will explain this.
- 33 × 54 (Figure 9.11a). This is estimated at 30 × 50 = 1500 and can be seen to be an underestimate, but reasonably close to the accurate answer.
- 42 × 78 (Figure 9.11b). Note that the 78 has been rounded up to 80 so that the length of the rectangle drawn is longer. This, then, is estimated at 40 × 80 = 3200 and can be seen to be very close to the accurate answer with the extra 2 × 40 not quite compensating for the 2 × 78.
- 51 × 92 (Figure 9.11c). Subtract to refine the estimate. Note that the 92 has been rounded up to 100. This is estimated at 50 × 100 = 5000 and can be seen to be an overestimate with 8 × 50 (which has to be subtracted) bigger than 1 × 92 (which has to be added).

Figure 9.11 Area models to illustrate estimation.
Extension
The principle of the algorithm for a two‐digit times two‐digit calculation can be readily extended to a three‐digit times three‐digit calculation and so on. The spatial organisation problems may require the child to work on squared paper or paper with vertical lines. In the easier examples the child may benefit from writing or articulating what each partial product means. Equally the principle of developing work from manipulative aids, through visual models, to symbol work is applicable to ‘harder’ examples.
These procedures integrate multisensory experiences with sound mathematical algorithms and provide the child with some concrete experiences and visual images that will help him to remember what might otherwise seem to him to be a meaningless random process. The structure provided by the identification of the partial products, and the number of partial products involved, helps the child and should help you, the teacher, with the diagnosis of errors and subsequent remedial input.
The area model will be used again in algebra with examples such as (x + 4)(2x − 6). Much of mathematics has a developmental structure and thus the foundations must be secure to underpin progression.
