4
Testing and Diagnosis
Teaching and diagnosis are inextricably intertwined. If you are working with an individual student, then a diagnostic approach to teaching must be inevitable. You need to appraise the student’s skills and deficits in mathematics as an ongoing activity. As soon as teaching begins, diagnosis begins.
It is the authors’ experience that children often know more than most tests reveal; for example an algorithm may be almost mastered, but a small misunderstanding causes failure and it is only the failure that is noted. As we have said before, intervention often needs to start further back than one might initially think, but not necessarily always from square one, and testing should bear this in mind and try to find the optimum place to start the intervention.
If you are working with a group of students you can still build in an ongoing diagnostic approach to much of the work you do by designing at least some of the exercises, worksheets and tests you use to give you that diagnostic information. One way of doing this is by examining error patterns (Engelhardt, 1977; Ashlock, 2010).
After considering some theoretical background, this chapter suggests a testing procedure. There could be many other equally valid procedures (e.g. Dowker 2001) and any procedure should be flexible enough in structure to respond to the child’s answers rather than rigidly following a fixed protocol.
Chinn (1992) has discussed the use of testing, in particular the benefits and disadvantages of norm‐referenced and criterion‐referenced tests. Kubiszyn and Borich (2007) provide an interesting overview of performance tests. However, before returning to this discussion, we should step back and ask the obvious and fundamental question, ‘Why test?’ Some of the answers to this question include:
- Parents may wish to know how their child’s achievements compare with those of his/her peers.
- A teacher may wish to monitor the progress of his or her group and/or identify those who need extra help and/or collect data with which to stream groups.
- There may be a need to measure rates of progress of an individual or a group.
- To measure the efficacy of the teaching programme/intervention.
- There may be some mandatory requirement to test.
- The test may be used to assess the ability of the child to progress to higher levels of study or to a new school.
- The test may be used to award a certificate recording a level of achievement.
- It may be used for diagnostic reasons (e.g. to find the child’s strengths, weaknesses, knowledge base and learning style) and thus identify a pupil’s special needs.
It is understandable for a parent, or indeed a concerned educator, to wish to have an idea of the depth of a child’s problems, measured in terms of a direct comparison with his peers. Tests which are ‘normed’ against a large population of children are used for these comparisons, for example the Mathematics Competency Test (Vernon et al., 2002), the Basic Number Screening Test (Gillum et al., 2012), the Wide Range Achievement Test: 4 (Wilkinson and Robertson, 2006) or the 15‐minute Screener Test (Chinn, 2017a) (see the References and Appendix I for details). It is not the function of these tests to provide a diagnosis of ‘dyslexic’ or ‘dyscalculic’ problems. If the examiner wishes to derive a diagnostic profile of the child’s strengths, weaknesses and learning style, additional testing will have to be done. The standardised test only sets the baseline for the diagnosis.
Criterion‐referenced tests are more diagnostic (by design) than norm‐based tests. Interpretation of a criterion‐based test can identify particular tasks that the child can and cannot do, but not necessarily his error patterns (Young and O’Shea, 1981; Ashlock, 2010) or why he can or cannot do a particular task. Such tests can be lengthy if they are designed to be thorough and/or cover much ground (see Wilson and Sadowski, 1976).
If these tests are used with groups, say as a class test, then the accurate interpretation of an individual child’s errors can be uncertain and relies heavily on how much of his method the child has documented. Of course, if the test is administered to an individual, then diagnostic questioning can be used to supplement the written evidence. As in the Test of Thinking Style in Mathematics (Chinn, 2017a), the key question is, ‘How did you do that?’ possibly followed by, ‘And can you think of another way it can be done?’ Careful, knowledgeable, well‐timed and informed questioning is usually non‐threatening.
Bryant and Reivera (1997) sum up the assessment structure with four questions:
- When push comes to shove, the following questions should guide our assessment practices:
- Where do students stand in relation to their peers?
- What do students know and what don’t they know?
- Why do students perform as they do (i.e. how on earth did they come up with that answer)?
- Is what I am teaching working?
Gillum (2012) offers guidance on assessment of dyscalculia and maths learning difficulties for educational psychologists, the group that are so often at the front line for diagnosis of specific learning difficulties.
We are avoiding entering the debate on the use of labels. It is an interesting debate. The stakes are high for some children and adults and there are many arguments and counter‐arguments for their use. We believe that key considerations are the child (adult) and the situation. It is a very real issue for the person concerned and academic theorising may sometimes overlook the realities.
A Diagnostic Test Protocol
In our ideal world the diagnosis/assessment would be carried out by a skilled and experienced person rather than a computer. So much of the information gathered comes from the nuances.
This diagnostic procedure, structured for a dyslexic or dyscalculic child, links back, as does all the work in this book, to a knowledge of the child and what he brings to the subject. The procedure is designed to be appropriate to the child and to the mathematics he is likely to encounter. It also relates to the teaching strategies described in this book, indicating which are likely to be more effective for the child. Although the test items suggested here have been carefully selected, they are by no means meant to be definitive and thus should be modified to suit the individual. The structure and rationale of the test should, however, act as a guide.
The diagnostic procedure will examine the child’s knowledge of basic facts, his levels of understanding of fundamental concepts (such as place value), his use of strategies and his thinking style, and it should provide the examiner with enough information to construct a teaching programme appropriate to the child’s needs.
The basic structure of the test protocol suggested below is designed to measure the child’s present level of achievement and to ascertain why and in what ways the child is having difficulty. Although the basic premise must be that each child is a unique individual, there are certain common areas that are likely to create difficulty for the dyslexic or dyscalculic learner (see Chapter 2). The protocol is designed to investigate these areas and to provide the examiner with a profile of the child’s mathematical abilities. The test is aimed at early mathematics and therefore concentrates on numeracy. It is primarily designed for an age range from around 8 to about 15 years, depending on the extent of the deficit, but it should be easy to modify some of the content to extend this range upwards. The test need not be given in one session, but may be spread over whatever time the examiner considers manageable for the child. Some items will be easier than others (which is information in itself). The examiner should unobtrusively encourage the child to try his best and certainly avoid any pressure with regard to speed of working.
Structure of the Diagnostic Protocol
The test structure includes most or all of the following components:
- A norm‐based (standardised) test (see Appendix 1)
- Counting/adding on tasks
- Number bonds (combinations)
- Times table and division facts
- Place‐value tasks
- Mathematics vocabulary and language
- The four operations
- Money
- Word problems
- Anxiety
- A thinking style test
- Working and short‐term memory
There are several standardised tests to choose from (see Appendix 1 for suggestions). The individual requirements of each examiner will probably reduce the choice. It is worth having several tests at the ready as many dyslexic children have a long history of being tested and may well have done your first choice recently.
Counting and adding on tasks
A good starting point is to scatter about 30 one pence coins or chunky counters on a table top and ask the child to estimate how many are there and then ask the child to count them. The test is looking at sense of number (estimation), one‐to‐one correspondence, speed of counting, accuracy and whether or not the child groups the counters/coins and in what size of group.
This is a good introductory item since there is not a right or wrong answer.
The examiner can also ask the child to count a (smaller) number of dots on a card, a task where he cannot handle and move the items he is counting. The dots can be presented in a regularly spaced line and then at random.
A series of fact cards may be made (on index or blank playing cards) and used to check basic addition and subtraction skills. When testing for basic addition and subtraction fact knowledge and strategies, the examiner should also be aware of the Einstellung effect (Luchins, 1942), which is the lack of flexible interchange between operations (add, subtract, multiply and divide) and which is observed when a child stays with the original operation even after the operation sign has changed (a behaviour that is different to misreading signs).
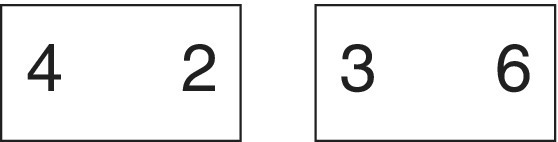
- 4 + 2 checks a basic, low number addition fact and whether the child counts on to 4, counts from 1 to 4 and then on to 6 or just knows the answer.
- 3 + 6 checks as above and to see if the child changes the order to the easier counting on task of 6 + 3.
- 4 + 3 = □ introduces the child to the ‘box’ for an answer, a number to make the question right. The examiner says, ‘What number goes in the box to make the right answer?’
- 5 + □ = 9 checks if the child is flexible enough in his knowledge of addition (and subtraction) to understand what is required, that is, does he count on or subtract 5 from 9 to obtain 4. The examiner asks ‘What number goes in the box to make this sum right?’
- 6 + 4 = □. The number bonds for 10 are an important set of data to learn, so the child’s level of knowledge of these facts needs to be checked.
- ‘Can you write three more pairs of numbers that add up to 10, like 6 and 4?’ Does the child immediately give you 4 + 6, or does he have a strategy such as the sequence 9 + 1, 8 + 2, 7 + 3?
- Give the child two 5p, six 2p and ten 1p coins and ask him to show you some ways of making 10p. Here the test is examining how many ways he produces 10p and whether he works to a system, for example 5 + 5 to 5 + 2 + 2 + 1 to 5 + 2 + 1 + 1 + 1, etc.
- 10 = 7 + □. Can the child use his number bonds for 10 in a different (subtraction) format?
- 8 + 7 = □. Many children, even if they say they ‘just know’ the answer, can be gently persuaded to tell you exactly how they worked it out. Some children will simply count on, using their fingers or objects in the room. The finger movements may be very slight, so the examiner will have to be observant. Some children extend their limited lexicon of facts by interrelating number facts. So 8 + 7 becomes 1 less than 2 × 8, or 2 less than 10 + 7.
- 9 + 8 = □, 9 + 6 = □, 9 + 4 = □. In asking this sequence (one at a time) the examiner is trying to see if the child has a consistent strategy for adding onto 9. Has the child started to see patterns?
- 17 − 8 = □. Checks a problem similar to those above, but presented as a subtraction.
- 60 − 6 = □. Can the child extend his number bonds for 10 to other ‘ten’ situations?
Times table facts
Pritchard et al. (1989) found that dyslexics had better retrieval of the two times, five times and ten times tables, so the protocol can acknowledge this. The examiner can resort to straightforward questions, especially if he has established a good rapport with the child. He can simply ask, ‘Which of your times tables do you know? ’ and maybe prompt, ‘The twos?’ The most frequent response is, ‘The 2s, the 5s and the 10s’ with some ‘smart’ kids adding on ‘The 1s and the 0s’.
If the child says he does know the two times table the examiner should ask, ‘What are seven twos, what is seven times two?’ The examiner must observe whether the child has instant recall or if he counts up 2, 4, 6, 8, 10, 12, 14 or if he uses a strategy, such as 5 × 2 and 2 × 2, added to make 7 × 2. Similar, careful diagnostic questioning can be used to establish a broad picture of the child’s times table knowledge.
The examiner may also wish to determine how many (if any) strategies the child uses to work out times table (and addition) facts. For example, if he knows that 2 × 8 = 16, does he add on a third 8 for 3 × 8, or if he knows 5 × 8 = 40, does he add another 8 to obtain 6 × 8? This can be checked by some leading questions. Another common strategy is to halve ten times table facts to obtain five times table facts. A child who has developed his own strategies is more likely to be aware of the interrelationships between numbers.
The commutative property is expressed as a × b = b × a, or in numbers, 7 × 8 = 8 × 7, that is, it does not matter whether a rectangle is 9 × 4 or 4 × 9, the area is the same (36). The commutative property is useful knowledge and worth including in a test procedure. If nothing else, it effectively halves the number of facts the child needs to remember. So a child may be asked to give the answer to 4 × 8 if he is told 8 × 4 = 32.
Formal, low‐stress, norm‐referenced tests for each of the four operations can be found in More Trouble with Maths (Chinn, 2017a).
Place value
The child is asked a series of questions. The numbers should be written on cards and shown to the child.
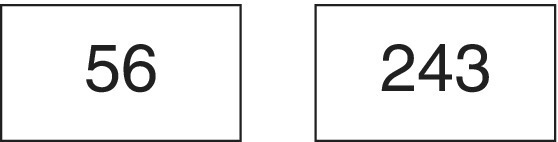
- If this number is fifty‐six (56), what is this number? 243.
- What is this number? 8572. Which digit tells us how many hundreds in the number?
- What is this number? 4016.
- Write (as digits) the number four thousand, two hundred and thirty‐three.
- Write the number sixteen thousand and seventeen in digits.
- What is the value of each digit in this number? 5656
- Work out 14 × 2, 14 × 20, 14 × 200
The vocabulary and language of mathematics
- The examiner needs two sets of cards, one set with each of × ÷ + − = the other set with add, divide, subtract, times, multiply, share, minus, plus, equals, same as, take away, more, less, difference. The child is asked to match the sign to the name. He can be told that there may be more than one name per sign. Make sure that the child can read the words. This checks the ability to relate the word to the symbol.
One of the most severely mathematically handicapped students we have ever assessed had significant speech and language difficulties.
- Ask the child to make up an addition (and possibly subtraction, multiplication and division) problem. The examiner may need to talk the child into this (e.g. ‘If we had 5 + 6, can we make that into a problem that uses words?’)
Concepts/understanding
- ‘Explain what you understand by the word divide (or multiply). Tell me how you would explain to someone what divide is.’ The examiner will have different levels of expectation for this depending on the child and may find that discussion can lead to a clearer picture of the child’s understanding of these deceptively simple concepts.
- ‘Give me an estimate, an easier number to use, for 97.’ The child may be bold enough to go to 100, but many will only go as far as 98. I have even known an answer of 76. The examiner is looking to see if the child has understood the need to make the estimate a number that is easy to use in calculations.
- Make up a word problem using in a mathematical way the word ‘share’.
The four operations (+ − × ÷)
Ashlock’s (2010) book Error Patterns in Computation introduces the idea of analysing a child’s errors and then providing appropriate remedial instruction. Careful selection of computation items should give useful diagnostic information, although it may not be possible to identify every error a student makes. This stage of the protocol also allows the examiner to introduce some criterion‐referenced items.
Chinn (1995b) has studied the errors made by 11–13‐year‐old dyslexic students. The one error type that dyslexic students made at a rate far above that of non‐dyslexics was the error of the ‘No attempt’. If there is no answer to a question then, obviously there can be no diagnostic information. This is a very important reason to keep the whole test protocol low stress. Smith (1996) also makes some interesting observations on errors, as do Young and O‐Shea (1981).
Some examples of basic criterion‐referenced tests are given below, but a teacher should set up their own criterion test battery based on their own circumstances, such as the type of student, the syllabus and the requirements for record keeping.
Addition
These questions can be presented on a worksheet. The questions must be well spaced out and preferably ruled off from each other. The child can be asked to make an estimate for each question first. The use of a worksheet format does not preclude the continued use of the question, ‘How did you do that?’
Checks two digit plus two digit with no ‘carrying’
Checks adding to a zero
Checks three digit plus three digit with two ‘carries’- 8 + 5 + 7 + 5 + 1 + 9 + 2 checks if the child uses number bonds for ten and pairs the numbers, rewrites the problem vertically, finger counts, tries to use memory as he adds in order, uses tallies, either to count each unit or as ‘carries for tens’. In other words, does the child overview the question or simply start adding at the first two numbers.
Subtraction
Another example of helping the examiner to look at methods and errors instead of just whether the answers are right or wrong. Indeed both sets of questions were chosen to investigate the typical errors a dyslexic or dyscalculic student may make.
Checks two digit minus two digit with no renaming (renaming refers to changing 46 to 30 and 16)
Checks two digit minus two digit with renaming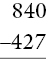
Checks three digit minus three digit with subtraction from zero
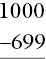Checks use of the renaming algorithm as opposed to rounding up the 699 to 700 and then adjusting the (interim) answer
Again the questions are designed to investigate the typical errors dyslexics, dyscalculics and many other children may make.
Multiplication
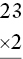Checks two digit times one digit with no carrying (using easy number facts)
Checks two digit times one digit with carrying
Relates to the first example to see if child can extend times 2 to times 20
Checks two digit times two digit
Checks three digit times three digit; also if the middle line of the ‘traditional’ method is written as 000, that is, unthinking/mechanical use of an algorithm
Note that, although these examples are ‘easy’ they allow the child to demonstrate his ability to solve the problem without failing because he does not know times table facts beyond two, five and ten. They also provide the examiner with information about the way the child solves basic multiplication problems and his error patterns beyond not retrieving basic facts.
Division
- 2)46 Checks two digit divided by one digit with no carrying
- 2)74 Checks two digit divided by one digit with one carry
- 5)56 Checks two digit divided by one digit with remainder (or decimal
- 2)4008 Checks dividing into numbers which include zeros
Again the information required centres on methods and number concepts rather than basic fact knowledge.
Word problems
Word problems should not be solely a test of reading ability, although the examiner needs to know if this is another barrier to success in mathematics. Again, the worksheet should be designed to be clear, uncluttered and accessible. The following examples are progressively more challenging.
The child is asked to read and solve the problems.
- What is 7 add 3?
- What is 49 minus 7?
- Take 12 from 25.
- If six boxes contain 2 pens each, how many pens altogether?
- Mike has ten red pens, three paper clips and seven pencils. How many things can Mike use for writing?
- Pat goes to the shop and buys two sweets at 5p each and ten sweets at 3p each. How much does she pay?
- Sally and Kath have twenty‐two model cars to share equally between them. How many do they each get?
- Questions 1 and 2 are the simplest and most straightforward.
- Question 3 reverses the order in which the numbers are to be subtracted.
- Question 4 mixes numbers as digits and numbers as words.
- Question 5 contains extraneous information.
- Question 6 has more than one stage.
- Question 7 is asking the child to divide and does not include any digits, the numbers are written as words.
Thus, each question probes a different aspect of the child’s knowledge and abilities. His answers should give the examiner a good picture of the child’s expertise with basic word problems. Although the questions are presented as a written exercise, once again the examiner can ask, ‘How did you do that?’ It is worth noting that word problems that require two stages/steps are often very problematic for dyslexics, dyscalculics and indeed many other learners, too.
Money
Knowledge of money is a survival skill. It is also interesting to see how a child’s ability to solve money problems compares with his ability to solve equivalent number problems. Later, the child’s knowledge of money problems can be used, for example, to work with decimal fractions (see Chapter 10).
- How many pence in one pound?
- How much is half of a pound?
- Show the child a card with £1.00 − 24p and ask him ‘How much change is there from a pound if a bar of chocolate costs 24p?’
- Show the child a card with £100 and £19 written on it and ask, ‘If you have £100, how many computer games can you buy if each game costs £19? Do you have any change? How much?’
- You have £5 and you want to buy four things that cost (show the child a card with £1.50, £2.50, 75p, 70p). Have you enough money to buy all four things?
- Question 1 checks basic knowledge (essential to complete the other questions).
- Question 2 is asking if the child has absorbed what 50p is.
- Question 3 is ‘real’ life mathematics and looks at subtraction.
- Question 4 is asking if the child has a concept of the value of money. Does he know that £100 is an identifiable amount of money.
- Question 5 is looking at another typical ‘shopping’ exercise and requires two stages.
Attitude and Anxiety
It may also help and encourage the child if he is asked questions such as the following:
- ‘How do you like mathematics?’
- ‘Do you think you are any good at mathematics?’
- ‘Are there any bits you are quite/especially good at?’
- ‘Which bits of maths do you like best?’
- ‘Are there any areas where you think you could do with a little extra help?’
Of course, the child may have given many clues during the interview, such as, ‘I could never do division.’ The teacher should be particularly observant of any comments that give clues as to the child’s attributions (see Chapter 2).
Note that there is a standardised test of maths anxiety in secondary age students in More Trouble with Maths (Chinn, 2017a).
Thinking Style or Cognitive Style
For diagnostic ideas see Chapter 3.
Tests for Dyscalculia
Currently this remains an area where there is little choice of tests. Butterworth’s (2003) Dyscalculia Screener is exactly that, a screener, administered individually via a computer and based on Butterworth’s model of dyscalculia. Emerson and Babtie’s (2010) The Dyscalculia Assessment offers a comprehensive collection of diagnostic activities for primary‐aged children.
As the concept evolves, as it will, as new researchers follow Butterworth’s pioneering work, then the testing is likely to evolve, too.
More Trouble with Maths. A Complete Guide to Identifying and Diagnosing Mathematical Difficulties (Chinn, 2017a) contains a number of tests, some standardised, covering many of the factors that will contribute to dyscalculia (and mathematical learning difficulties) so that a decision is based on a range of data. It is closely structured around the test protocol outlined in this chapter.
Summary of the Test Protocol
The answers to the questions from the various strands of the protocol, combined with a knowledge of the way the child solves each question, should provide the examiner with a comprehensive picture of what the child can do and how he does it, so that the examiner has a measure of the child’s number and operation sense, basic knowledge and his appropriate use of numeracy skills. The child’s cognitive style can be deduced from such behaviours as to whether he finger counts to solve 8 + 7 or if he uses (2 × 8) – 1 or 7 + 7 + 1, his estimate for 97, or how he solves 1000 − 699. As well as providing a picture of the child’s strengths and weaknesses, the protocol helps you as the teacher to obtain a clearer idea as to what strategies the child is likely to find easy to adopt and which he will find hard to absorb.
The protocol described here is a guide to a structure for diagnosis. As a tester gains experience he will adapt these ideas and introduce new questions, which enable him to follow where the child’s responses lead. It should be the goal of the teacher/tutor to construct a diagnostic protocol that is appropriate to their own educational environment.