11
Fractions, Decimals and Percentages: An Introduction
Introduction
The mathematics dealt with in the previous chapters has been concerned with using numbers to describe things. This chapter is about describing parts of things with numbers. There are three ways mathematics goes about this task, fractions, decimals and percentages, with important differences and similarities between the three forms. Each form is dealt with in a chapter of its own, but this chapter describes the essential characteristics of each and how they interrelate.
‘Fractions’ is a topic which causes difficulty for learners across the world and considerable anxiety for adults. In developing the Test of Cognitive Style (1986), we had to take out an item on fractions because it caused so much anxiety in the trials. Subjects would just stop at that item and not attempt any more items, even though they were not about fractions.
However, we do use some fractions, mainly half and quarter, in everyday life; decimals, mainly for money, for example £4.63 or $13.99; and percentages for example, as interest rates for money and for discounts, for example ‘up to 70% off’ at sale time in shops.
This chapter will explore the relationship between these formats in an attempt to strengthen an understanding of each format. As ever, we will work from the familiar to the new, so our key relationship will be:
All three are fractions, but that is only clear when the student knows the code. So, ½ means ‘one divided by 2’ or ‘one of two (equal) parts’. 0.5 requires a knowledge of place value. The 5 has a place value of five tenths, that is ‘five out of ten (equal) parts’. 50% requires an awareness that % means ‘out of 100’, so that 50% means ‘50 out of 100 (equal) parts’.
Fractions
Fractions are the most informative way of describing parts of things, but only if you understand the concept. For example, ⅝ tells you that the whole (of something) has been divided into 8 equal parts and that you have 5 of those parts. They are introduced in primary schools with an expectation from teachers and parents that children should be able to understand and work with fractions. Memories tend to be selective here since, as said above, we know that many adults have difficulties dealing with fractions. One of the main reasons for this is that fractions do not appear to do what numbers have previously done. They challenge the learner’s sense of consistency.
Fractions use two numbers to describe one quantity, but in a way that is a challenge to previous experiences with numbers. Thus, a half is written as ½, a quarter as ¼ and three‐quarters as ¾. The/in effect ‘hides’ the division sign. Similarly for a two‐digit number such as 67, the place value of the 6 ‘hides’ the × 10.
As an example of another apparent inconsistency, the addition of fractions challenges earlier experiences of addition (Skemp, 1971), as is illustrated below:
The addition sign operates on the ‘top’ numbers of the two fractions to be added, but not on the two ‘bottom’ numbers.
A further apparent inconsistency is with the series of fractions:
In this series, as the ‘bottom’ number gets bigger, the fraction value gets smaller.
For the first stage of teaching using concrete materials, we use paper folding to help to illustrate how fractions work. The folded‐paper methods described in this book are structured to guide the learner towards understanding fractions and the way we use symbols to represent them. Drawings of folded fractions provide a means of recording and communicating the processes explained by the paper version. They form the intermediate step between folded‐paper fractions and written fractions.
We recommend that square or close‐to‐square shapes be folded and drawn in all cases. We advocate folding in two dimensions, mainly to comply with our ongoing model of using area for (a times b) calculations.
Terminology
A fraction such as ⅘ will be referred to as ‘part’ of a whole thing. The fraction is made up of equal fifths, which will be referred to as ‘segments’, rather than as parts of the fraction. This avoids the duplicate use of the word ‘parts’, and children should be familiar with the notion of segments of an orange.
The terms ‘denominator’ and ‘numerator’ are confusing for many dyslexic and dyscalculic students. However, if students do wish to have a way of knowing which word means what, then it may help to see the structure of ‘denominator’ as having ‘nom’ or ‘name’ included (Brown et al., 1989). Denominators such as fifth or tenth or quarter can be seen as the name of the fraction, that is, the name that tells you how many segments.
What is a fraction?
Part of a whole thing
Start by discussing with students what they know about fractions, in particular, the ones they are familiar with in everyday life, which are usually a half and a quarter. Include in the discussion observations and questions such as the following:
Half of this square (or any object that can be divided exactly into halves and quarters) is bigger than a quarter, yet we write a half as ½ and a quarter as ¼.
Are there other ways we can write the fraction ½? For example, half of a pound (£) could be written as
or half of an hour as
.
What do we get when we add a half and a quarter?
What do we get when we halve a half?
How many halves are there in a whole, that is, in one?
How many quarters are there in a half?
How many quarters are there in a whole, that is, in one?
Can you have a bigger half (of a cake or pizza)?
Can you cut an exact half of a pizza or an apple?
These discussions set the basic rules for fractions and can be revisited for checking a procedure or an answer, possibly using the question, ‘Is it bigger or smaller?’
- The piece of paper in Figure 11.1a has one‐fifth shaded in. It is divided into five equal segments and one is shaded, so the fraction is written as ⅕, one segment out of five segments.
- The fraction in Figure 11.1b shows three‐quarters. The written version is ¾, three segments out of four segments.
Children can be asked to give the written form for other fractions, such as those shown in Figure 11.1c.
Figure 11.1 Folded paper/area models for fractions.
Whole things divided into equal segments
- Figure 11.2a shows a whole square of paper is ten tenths (that is why they are called tenths). This is written as
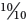= 1 whole square. The number at the bottom of the fraction indicates both the number of segments and the size of the segments. - The square in Figure 11.2b has been left as a whole. It can be written as
= 1 and called one whole.
Children can be asked to write down the fraction for given examples, such as those shown in Figure 11.2c.
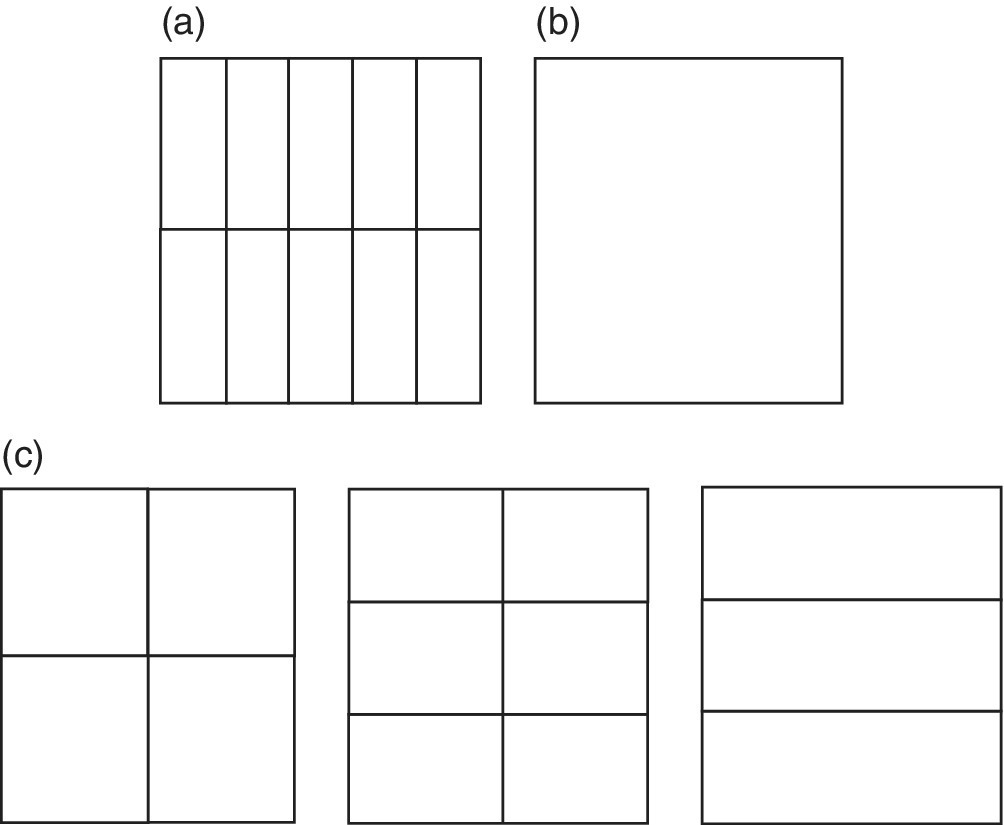
Figure 11.2 Folded paper/area models for fractions.
- The special name for the segments in Figure 11.3a, halves, should be highlighted.
- The segments in Figure 11.3b are usually known as quarters, but calling them fourths as well at the beginning tells children more about them. A third is also a linguistic exception.
- The version of fourths/quarters shown in Figure 11.3c should also be recognised by the children.
Figure 11.3 Folded paper/area models for fractions.
More than one whole thing
- Figure 11.4a shows two squares left as a whole. This can be written as
. - Figure 11.4b shows two whole squares divided into quarters. This can be written as 2 ×
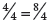. - The square in Figure 11.2b has been left as a whole. It can be written as 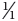= 1 and called one whole.
Figure 11.4 Equivalent fractions for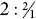 
and 
.
Making fractions
It is important that children make fractions themselves by folding paper squares. This will help to avoid fundamental misconceptions such as the idea that halving, halving and halving again will produce sixths. Demonstrably, it produces eighths. It will also help in case of any future difficulties if children can recall how the fractions were made.
The ‘halving’ procedure, making halves
Figure 11.5a shows the folding procedure that produces halves. If the procedure is repeated, then it shows that halving and halving again makes quarters (Figure 11.5b). Repeated halving produces a family of fractions, whose subsequent members are eighths, sixteenths, and so on.
Figure 11.5 Folding paper to show halves and quarters.
The ‘thirding’ procedure, making thirds
The procedure shown in Figure 11.6a produces thirds. Repeating the procedure will produce a family of fractions, the next member of which is ninths.
Figure 11.6a Folding paper to show thirds.
The ‘fifthing’ procedure, making fifths
The procedure shown in Figure 11.6b produces fifths and repeats to produce twenty‐fifths, and so on.
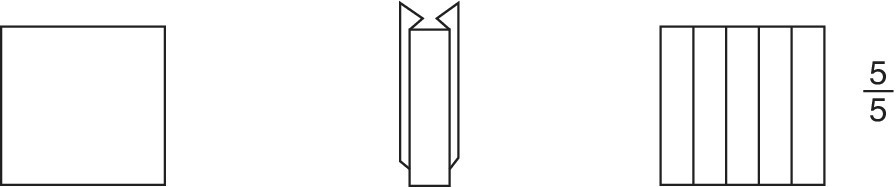
Figure 11.6b Folding paper to show fifths.
Other procedures
A new procedure is required every time the number of segments is prime: 
, and so on.
In practice, halves, thirds and fifths are sufficient, because sevenths, elevenths, and so on, are very rarely needed, and are undesirable in the early learning stages.
Some teachers refer to these folding procedures as ‘machines’, for example the ‘halving machine’.
Other fractions
Other important fractions can be made using a combination of folding procedures.
- Sixths – made by halving and thirding in either order.
- Tenths – made by halving and fifthing in either order.
- Twelfths – made by halving, halving and thirding in any order.
- Twentieths – made by halving, halving and fifthing in any order.
Table 11.1 summarises how to make all the fractions that are likely to be relevant at this stage
Table 11.1 How to use folding to make the basic fractions.
| Fraction | half | half | half | half | third | third | fifth |
| half | * | ||||||
| third | * | ||||||
| quarter | * | * | |||||
| fifth | * | ||||||
| sixth | * | * | |||||
| eighth | * | * | * | ||||
| ninth | * | * | |||||
| tenth | * | * | |||||
| twelfth | * | * | * | ||||
| sixteenth | * | * | * | * | |||
| twentieth | * | * | * | ||||
| thirtieth | * | * | * |
Equal or equivalent fractions
Fractions are equal (or equivalent) if they cover the same amount/area of a paper square, that is, they have the same value. For example, Figure 11.7 shows that:
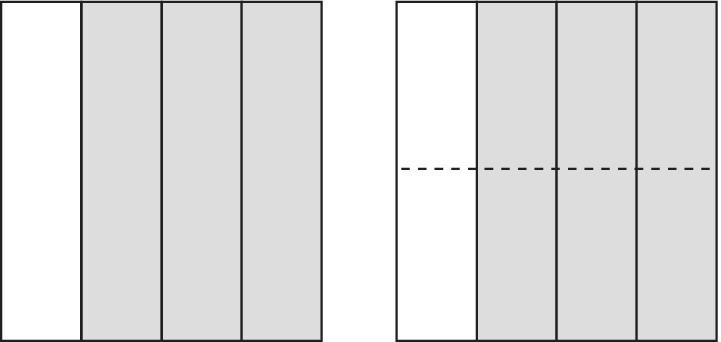
Figure 11.7 Equivalent fractions 
and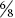 
.
The extra (horizontal) fold has produced twice as many segments, though the new segments are smaller (half the size). The written format that gives the same effect is:
The image shows that the number of segments has doubled, from four to eight, and the number of shaded parts has doubled, from three to six. The size or value of the fraction, as shown visually, has remained the same.
The top and bottom numbers of the fraction can be multiplied by the same number without changing the value of the fraction. The procedure is actually multiplying by one. Multiplying by one does not change the value of the fraction. All of the fractions below have a value of 1.
There are many different types of exercise for establishing this concept.
Children can be asked the following questions;
- Give the written form for the two equal/equivalent fractions shown in Figure 11.8a.
- Draw in the extra fold lines in Figure 11.8b to show that
. -
Write the correct numbers in the empty boxes:
Figure 11.8a Equivalent fractions 
and 
.
Figure 11.8b Fold to show that 
.
Simplifying fractions
Example
In the example shown in Figure 11.9, it is possible to combine the tenths into groups of two, as shown, reducing the number of segments to five. Consequently, the four shaded parts (tenths) are reduced to two (fifths). The written format that gives this effect is:
Figure 11.9 Simplifying fractions: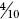 
= ⅖.
If the top and the bottom of a fraction are divided by the same number it does not change the value of the fraction. This is dividing by one and that operation does not change the value of the fraction, even though it is now composed of different numbers.
A practical problem, here, is to decide what number to use for dividing the top and the bottom, that is, into what size groups can the segments be divided. Prime factors can be used, or trial and error (based on a knowledge of the multiplication/division facts), but the method consistent with the philosophy of this book is to try the numbers used in forming the original segments by folding.
In the example above, tenths would have been formed by folding into halves and fifths. Therefore, dividing into groups of two or five should be tried. Of these, only the groups of two work for the shaded segments, to give the fraction in its ‘lowest terms’.
Example
Simplify 
. For this example, if the pupil recognizes that twelfths would be formed by folding into halves, halves and thirds, then dividing by 2, 2 and 3 should be attempted:
Alternatively, since 8 and 12 are even numbers then dividing by two is possible. This gives 
where again the numbers are even, so division by two is again possible.
Once ⅔ has been reached, further dividing of top and bottom numbers by 3 or 2 is not possible, so the fraction is as simple as it can be made.
Since halving and halving again produces quarters, a short cut would be to try dividing directly by four, as illustrated in Figure 11.10.
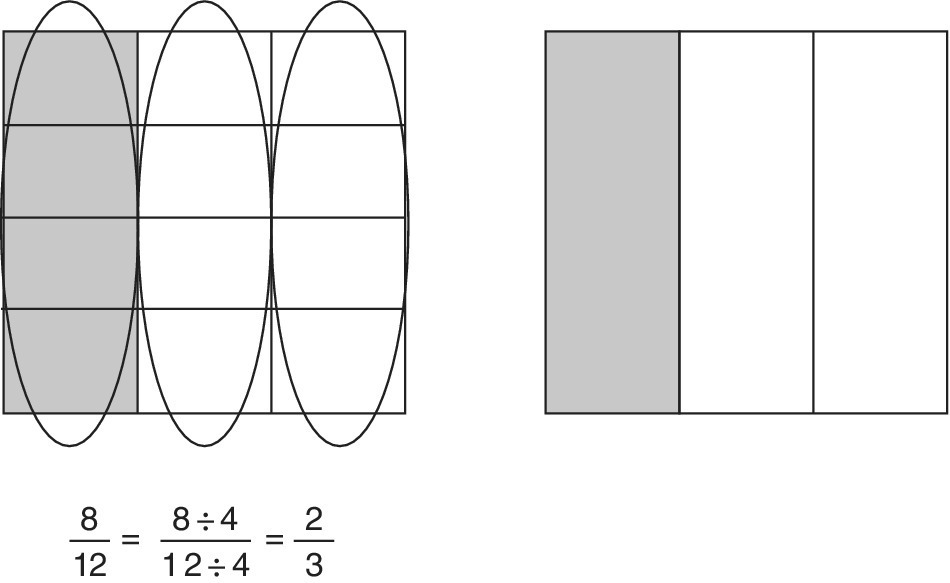
Figure 11.10 Writing
in its simplest form.
There are many different types of exercises that can be used for establishing this concept, for example:
- What are the folding steps that would make the fraction in Figure 11.11?
- Write the correct numbers in the empty boxes:
Figure 11.11 What folding is needed to make this fraction pattern?
Another strategy is to use the times tables square. In Figure 11.12 the columns for four and seven have been italicised. Horizontal pairs show equivalent fractions:
Figure 11.12 The times tables square and equivalent fractions.
Decimals
Decimals are also used to represent parts of a whole thing.
Where a number is composed of whole and parts, the decimal part is separated by a decimal point, for example 37.651.
Basically decimals are just specific fractions – the first column after the decimal point representing tenths, the second representing hundredths, the third representing thousandths and so on. However, because of this, each column (tracking right to left) is ten times the place value of the previous column, making decimals a continuation of the place value system. This property is apparent, for example, when a number is carried in an addition, or when a decimal is multiplied by ten.
First decimal place as tenths
This can be demonstrated well with a measuring exercise. Consider the length AB marked against a scale (Figure 11.13).
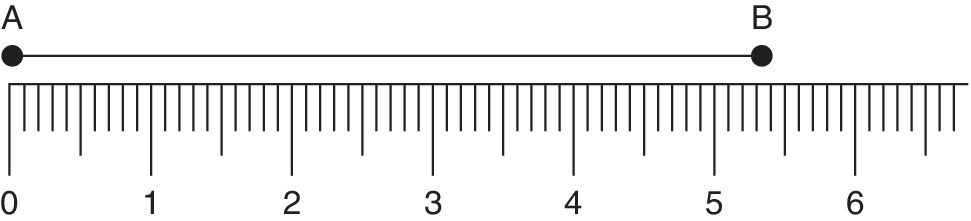
Figure 11.13 Using a rule to show 5.3.
- Each large unit on the number line is divided into ten smaller units.
- Each smaller unit will be
of a large unit. - The length AB is 53 small units and 5
large units. - If AB is written as 5.3 large units, then .3 means and the first number after the decimal point represents tenths.
- 5.3 is five units and three tenths of a unit.
Second decimal place as hundredths
This can be demonstrated with examples using money/coins.
Almost all children will accept and understand the above equivalents for money units. The amount of money illustrated in Figure 11.14 is written in pence at the top and pounds at the bottom.
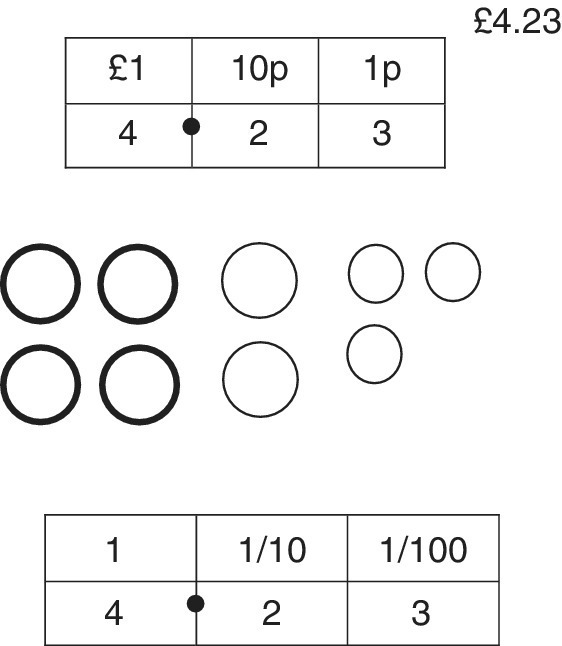
Figure 11.14 Ways to visualise 4.23.
When the amount of money is in pounds and pence, the decimal point takes up the position we see in prices. Figure 11.14 shows that the first column after the decimal point is for tenths and shows that the second column is for hundredths.
Further decimal places
Once the fraction equivalents are established for the first and second decimal places, it is relatively easy for children to accept the next place as thousandths, and so on. A practical illustration could use a metre rule with millimeter markings. A reminder that the familiar whole‐number column headings are: thousands, hundreds, tens, ones is usually helpful. It is worth explaining that the decimal point is not the centre of symmetry in:
Thousands hundreds tens ones. tenths hundredths thousandths
The centre of symmetry is ‘ones’.
If the numbers are shown as powers of ten, this puts 1 as 100 in the centre of the series.
| 103 | 102 | 101 | 100 | 10−1 | 10−2 | 10−3 |
| 1000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1000 |
In the early stages of developing an understanding of decimal numbers and decimal place value, difficulties will be reduced if children can be persuaded to write their examples down in place value columns with headings.
Converting decimals to fractions
As was outlined earlier, decimals are composed of the specific fractions 
and so forth, depending on the place value column(s) in which they are written. To convert them back to fractions, read off which of these columns in which the digits are placed. Examples are given in Figure 11.15.
Figure 11.15 Linking decimal numbers to tenths, hundredths and thousandths.
Examples that can be simplified
After some decimals have been converted into fractions, they can be simplified.
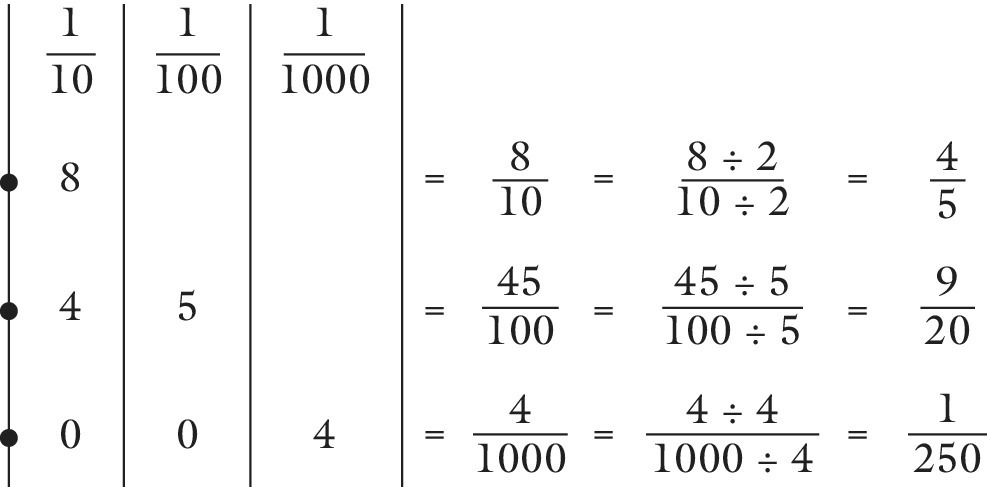
Use of the number 25
In many cases where decimals have been converted into fractions and are to be simplified, the ability to divide (top and bottom) by 25 is a useful short cut. There are two in 50, three in 75, four in every 100 and so 40 in every 1000. For example:
Special decimals
A few decimals can be converted and simplified to very important fractions. It is useful if these can be memorised:
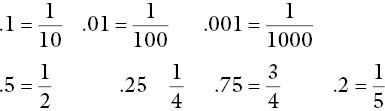
The significance of zeros
Zeros are used to hold digits in their place value position in a number. With decimals, zeros are sometimes used in situations where they have no impact on the value of the number, for example 0.50. Neither zero in 0.50 has an impact on the place value of the five. In the number 0.05, the second zero (after the decimal point) has ‘pushed’ the five into a hundredths place value position. It does have an effect on the value of the five.
With whole numbers the equivalent situation would be, for example, 8, 08 and 80. We rarely write 08. The zero has no impact on the place value of the 8, but with 80, it moves the 8 from the ones place to the tens place.
When a decimal, such as .92 has no whole‐number part, it is usually written in the form 0.92, with an optional zero at the front, as a matter of style and to draw attention to the decimal point. As long as children are having difficulty with decimals, simplicity is more important than style, so it could be argued that this should be avoided. In this chapter, such zeros have been omitted for this reason.
In general, just as for whole numbers, the significant zeros are located between other digits, or between a digit and the decimal point. The unnecessary or optional zeros are to be found beyond those numbers furthest from the decimal point.
The following examples demonstrate the role of zero in decimals:
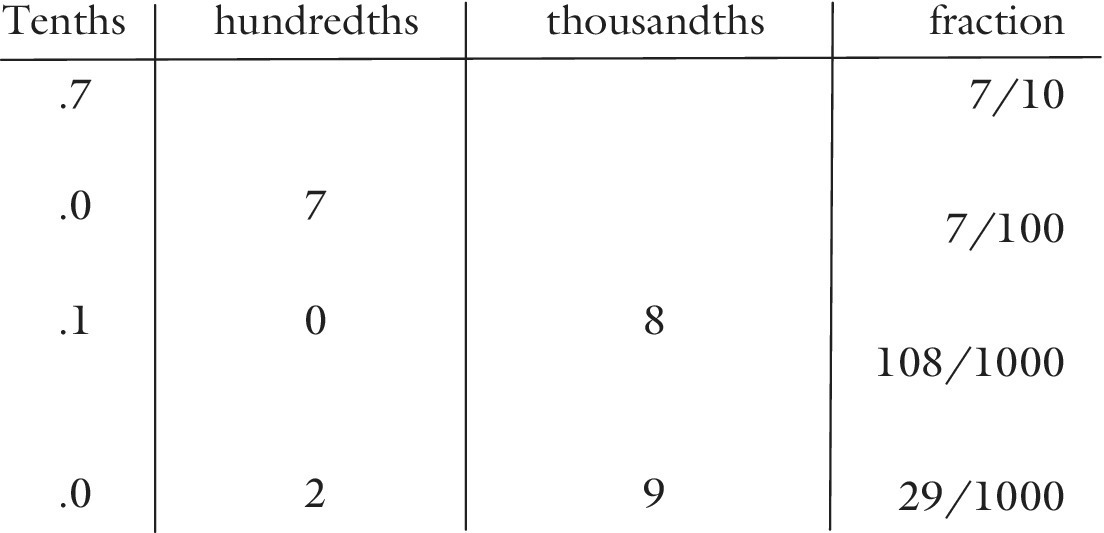
Comparing decimals
‘Which decimal is bigger, .87 or .135?’ In answer to this question, many children will give the answer .135, because they see 135 as being bigger than 87. Of course, they are not comparing like with like, because the 135 are thousandths whereas the 87 are hundredths. The decimal numbers have challenged their sense of consistency. For whole numbers a three‐digit number is bigger, has greater value than a two‐digit number. By way of explanation, write the decimals in their place value columns and give them the same number of digits by using zeros that have no influence on value:
This process has the same effect as making segment sizes the same for fractions. Now 870 is clearly bigger than 135.
Some children have a similar problem understanding why .25 is halfway between .2 and .3, both of which may seem smaller. The column headings and optional zeros can help again:
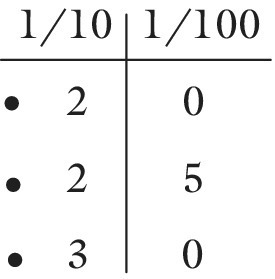
This shows that 25 hundredths is halfway between 20 hundredths and 30 hundredths.
This can also be modelled with Dienes blocks. The thousand cube becomes one, the flat becomes a tenth, the long becomes a hundredth and the small cube becomes a thousandth. If, despite explanations, this new interpretation confuses the learner then it will not help.
Another approach to these and other similar problems is to explain with a decimal number line, such as is shown in Figure 11.16. This number line shows that .87 is bigger than .135. The equivalent fractions above the line provide further justification. It also shows that .25 lies halfway between .2 and .3, another such situation being observable at .865, which is halfway between .86 and .87.
Figure 11.16 A number line for decimals.
Decimal number sequences
Decimal number sequences can be regarded as extracts from a number line, such as in Figure 11.16. If the examples are selected carefully, they can provide a very convincing alternative way of looking at problem areas that may not have been fully understood. One such problem area is tackled below. Consider the following sequence:
Those children who have not properly taken on board the message that decimals follow place value rules, just as whole numbers do, may make the mistake of assuming that the next decimal in the sequence is .100. They have not understood that the 1 digit from 100 has to move up in place value to produce 1.00.
Another explanation can be provided by approaching the sequence from the other direction, working downwards, for example:
This also reminds students about using working backwards as a way of checking answers and about the relationship between addition and subtraction.
Each of the following sequences straddles a potentially awkward region, where the numbers in italics would be left out for the student to find:
| 1.7 | 1.8 | 1.9 | 2.0 | 2.1 | 2.2 | 2.3 | |
| 7.3 | 7.2 | 7.1 | 7.0 | 6.9 | 6.8 | ||
| 8.8 | 8.6 | 8.4 | 8.4 | 8.0 | 7.8 | 7.6 | 7.4 |
| 19.7 | 19.8 | 19.9 | 20.0 | 20.1 | 20.2 | 20.3 | |
| 20.03 | 20.02 | 20.0 | 20.00 | 19.99 | 19.98 | 19.97 |
Converting fractions to decimals
Some fractions are very simple to convert into decimals, because they are already tenths, hundredths or thousandths. They slot into the decimal columns immediately, like the examples below:
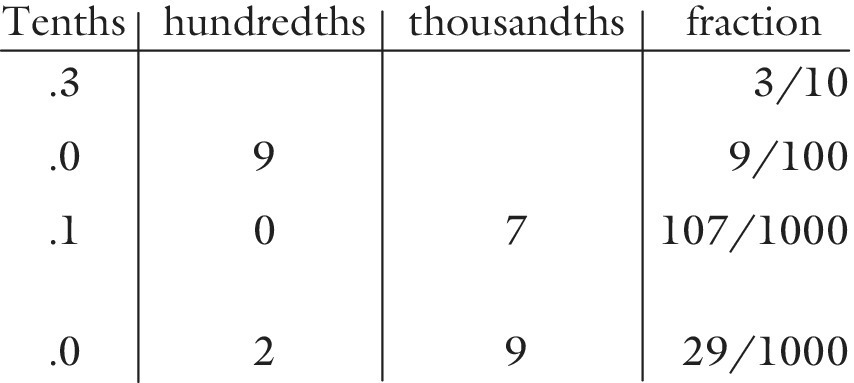
There are other fractions that can easily be made into tenths, hundredths or thousandths, as shown with the following examples:
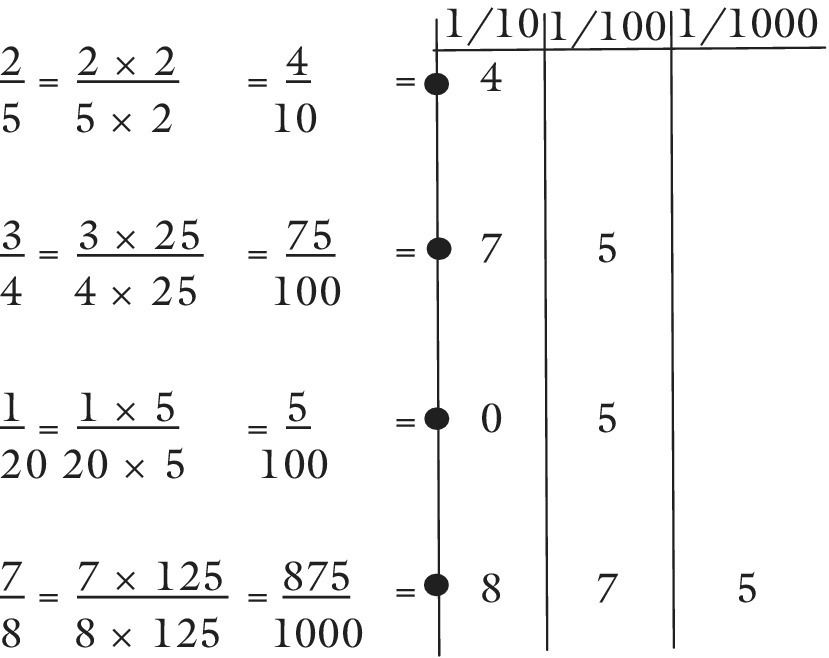
The final example, 
in the table above, depends, for its conversion, on the knowledge that 8 × 125 = 1000. Lack of this knowledge would push this conversion into the most difficult category, along with fractions such as 
. For such an example, it is necessary to regard as 5 ÷ 9, and to perform a decimal division, which is beyond the scope of this chapter, so such conversions are covered in Chapter 13.
Percentages
Percentages are another way of describing parts of whole things. ‘Percent’ means ‘out of a hundred’. For example, 1 percent means 1 out of a 100, which can also be written as 
. In essence, percentages are hundredths. The sign for percent, %, seems to be constructed from a 1, a 0 and another 0, so it behaves as a perpetual and valuable reminder of the importance of 100. Clearly, since percentages are hundredths, it is a simple matter to convert between percentages and fractions. Moreover, since hundredths constitute one of the decimal column headings, it is also easy to convert between percentages and decimals.
Percentages and whole things
Writing down whole things in terms of percentages is slightly more difficult with fractions or decimals, where whole numbers are just written separately, in front. However, there is subsequently much less need to manipulate the percentages, so the difficulty is not carried further. A whole thing is 
, which is 100%. Every whole thing is 100%, and so, for example, a whole number such as 5 is 500%.
An inclusive model for percentages, fractions and decimals
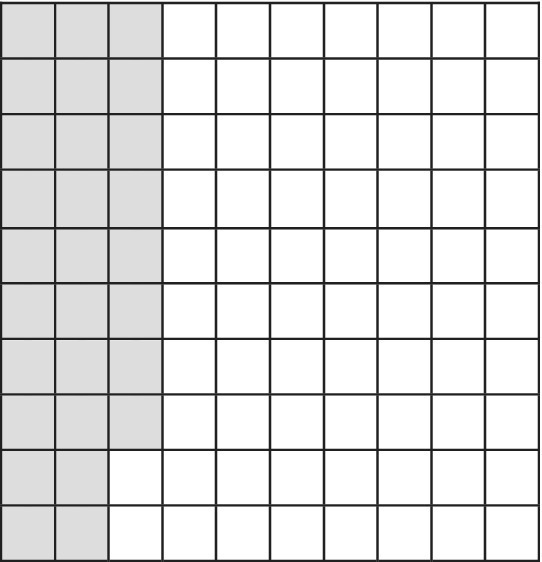
Figure 11.17 shows a whole square divided into 100 equal segments. Each segment is , or 1%, or .01 (1 in the hundredths place value column). These can be represented physically by the ones bricks in Dienes apparatus. Each column of ten ones is , or 10%, or .1 (1 in the tenths place value column). These can be represented by ‘longs’. The whole square is 100%, or 1 whole number, and could be represented by a ‘flat’.
Figure 11.17 A hundred square.
Percentages are a rather more palatable or accessible way of expressing parts of whole things for most people, perhaps because it seems easier for most people to visualise, for example, 39% as 39 out of their visual image of 100, rather than the symbols 
or .39.
Also, the values of percentages are much easier to compare.
Comparing percentages
Unlike fractions, which can have segments of any size, or decimals, which can be tenths, hundredths, thousandths, and so on, percentages all have the same segment size – they are all hundredths. Their numerical values can therefore be compared in a straightforward way – the bigger the number, the bigger the percentage (and the bigger the part that it represents).
Examples
- 38% is bigger than 26% (by 12%) (Figure 11.18).
- 19% is smaller than 22% (by 3%).
- 31.5% is bigger than 31%.
- 135% is bigger than 125%.
Figure 11.18 A hundred squares used to compare 28% and 26%.
Converting percentages to fractions
If percentages are understood to be hundredths, converting them to fractions is simply a matter of writing them as a fraction, with 100 as the bottom number (denominator).
Examples
.Sometimes the fraction obtained can be simplified.
Examples
.Some percentages produce fractions that need many steps to simplify.
Example
(See Chapter 13 for multiplying decimals by 10.)
Example
(See Chapter 12 for multiplication of fractions.)
Converting fractions to percentages
When fractions are hundredths, then a % can replace the denominator.
Examples
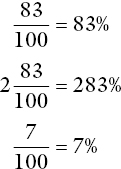
Some fractions have to be first changed into hundredths. (A similar step was necessary in converting fractions to decimals.)
Examples
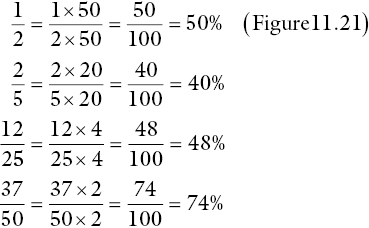
Figure 11.21 Equivalent fractions and percentages ½ = 
= 50%.
At times, children will be unable to change the fraction into hundredths, because they do not know the multiplier that will make the denominator 100. Finding this multiplier becomes the first step. Consider 
:
The question is ‘How many 20s are there in 100?’ This may help the student to realise that the equation needed is 100 ÷ 20 = 5. It is now possible to multiply the top and the bottom numbers by 5 and create hundredths:
Sometimes the numbers that make up the fraction create a division that is sufficiently complex to make the use of a calculator a pragmatic option. This should be backed up by an estimate. For example, 
can be rounded to 6/100 and thus give an estimate of 0.6.
Converting percentages to decimals
Percentages are hundredths, and the second column of decimals is for hundredths. Therefore, it is a relatively simple task to write a whole‐number percentage in the decimal columns of a place value card.
Examples
The final example above shows a harder decimal percentage. The digits go beyond the hundredths column because of the .25%. This needs extra decimal places, as far as ten thousandths, because:
Converting decimals to percentages
The second place value column for decimals is for hundredths. Therefore, any decimal that can be ‘lifted’ entirely out of the first two columns for decimals can be written immediately as a percentage.
Examples
Converting decimals to percentages
The second column of decimals is for hundredths. Therefore, any decimal that can be ‘lifted’ entirely out of the first two columns of decimals can be written immediately as a percentage.
Examples
If the decimal contains more than two places, then the percentage will have to be extended to contain them.
Example
Special percentages
The following list shows the equivalent percentages, fractions and decimals for the most important parts of a whole thing:
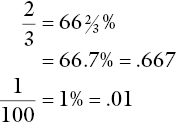
Overview
In order to practise the various conversion processes detailed in this chapter, the learner should convert the shaded parts on diagrams, such as those shown in Figure 11.23, to symbol format. The task should be to write the numbers as percentages, decimals and fractions (simplified where possible).
Figure 11.23 Write each of these as percentages, decimals and fractions.
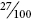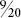