5
Concept of Number
Introduction
When a child has problems learning the basic facts of number, then his problems may be compounded by his consequent failure to develop an understanding of the values and interrelationships of numbers. Of course, it does not automatically follow that a child who successfully rote learns the basic facts will develop an understanding of numbers. It is important that any child should develop a ‘feel’ or ‘facility’ for number, that is, he needs to learn:
- A sense of the size or value of a number (Berch, 2005).
- A recognition of the other numbers which it is near to.
- How near a number is to other numbers, particularly the key/core numbers such as one, two, five, ten, twenty, fifty, hundred, thousand and so on.
- Whether the number is larger or smaller than other numbers, and by roughly how much.
- The relationship of the number to key/core numbers, which infers an understanding of the operations and their effect.
For children with dyslexia/dyscalculia/learning difficulties in mathematics, the development of this last facility is a likely alternative route for coping with the memory demands of early numeracy as suggested in the NRC’s Key Finding 2 (Bransford et al., 2000). An early failure to learn basic number facts from memory or by using efficient strategies can keep them from the range and quality of experiences needed to develop number concept. Of course, memorising the basic facts does not guarantee the development of a concept of number, so the compensatory ideas advocated here may benefit a wider population than just dyslexics and dyscalculics. We are trying to take the child beyond a total reliance on counting on and fallible memory.
The first number test on the NFER‐Nelson Dyscalculia Screener (Butterworth, 2003) is for subitising. This means an ability to look at a random cluster of dots and know accurately how many are there, without counting. It is the direct perceptual apprehension of the numerosity of a group. Most adults can do this with confidence for four items. The sub‐test is about a fundamental knowledge of number. The approximate number system (ANS) is what it says it is, an ability to approximately appraise the magnitude of a quantity or compare the magnitude of quantities without relying on language or symbols.
Using consistent and recognisable patterns for objects enhances the ability to recognise quantity, for example ten:

A person who has to rely entirely on counting for addition and subtraction is severely handicapped in terms of speed and accuracy. Such a person is even more handicapped when trying to use counting for multiplication and division. Often their maths work sheets are covered in endless tally marks and often they are just lined up, neither neatly nor grouped in fives as in the gate pattern 1111. Their maths is done by counting in steps of one. If you show these learners patterns of dots or groups as on dominoes or playing cards, they prefer lines of tallies. This is not just about the ability to ‘see’ and use five as a cluster. It is also the ability to see other number relationships such as nine being one less than ten, to see 5 + 6 as 5 + 5 + 1, to count on in twos, tens and fives, especially if the pattern is not the basic one of 10, 20, 30… but 13, 23, 33, 43…
As teachers we are trying to develop the ability to go beyond counting in ones by seeing the patterns and interrelationships in numbers (Chinn and Ashcroft, 2004).
This chapter looks at the very early stages of number work. These are the stages where a dyslexic or dyscalculic child may have started to fail or is failing to progress conceptually. Thus, even an older child may need to return to these early topics to recover the experiences he had not taken on board earlier. As with much of the material in this book, the work described is not age‐specific, but rather achievement specific. As a tutor/teacher, you need to adjust the style and approaches of your presentation of the work to avoid patronising the learner.
Early Recognition of Numbers and Their Values
To return to ‘subitising’, a small number of objects can usually be recognised instantly by using a visual sense of number, so that a child seeing two different clusters of, say, four spots will recognise them as the same quantity. This ability disappears with larger numbers (though some children and adults have been able to extend the skill to remarkably large numbers).
Slightly larger numbers may be more quickly recognised if:
- The objects are arranged in a recognisable patterns, or
- The number can be seen as a combination of other numbers. Thus, even at this early stage of development, the child can be introduced to the use of patterns and inter‐relationships.
So, for example, ten can be shown as in the two arrangements of five squares (as also shown above).

Teachers (or parents) can also introduce certain special numbers that can be used as landmarks, reference points or stepping stones towards understanding other numbers, for example ten. Then five can be seen as half of ten, nine can be seen as one less than ten, twelve can be seen as two more than ten and twenty as two times ten. Coinage the world over uses key numbers for its values, almost always using 1, 2, 5, 10, 20, 50, 100 and so on. Other numbers and values are constructed from these key coins. For example, the lack of a coin worth 7 does not handicap the manipulation of money for something that costs 7. A 5 coin and a 2 coin can be used.
The Language of Mathematics (see also Chapter 2)
In this chapter, we use the word ‘number’ to mean one of the following:
- The mathematical symbol for the number, for example 8
- The written form of the number word, for example eight
- The sound of a number word, for example ‘ate’
So already we are using three interpretations of even such a basic word as ‘number’.
For most of the dyslexics and dyscalculics we teach, the problem of mathematics as a ‘foreign’ language becomes particularly acute when there is a necessity to write numbers down. The situation is exacerbated by the conventions of place value (base ten). As an example, we have seen 11‐year‐old boys write ‘six hundred and five thousand and twenty’ as:
600500020 and as a slightly less obvious error, but still based on a rationale, 5620.
It is worth remembering the linguistic confusion that surrounds the first two digit numbers, ten to nineteen. Sadly the inconsistencies of these ten numbers confuse many children and act as the first (and thus possibly dominant) experience of a failure to understand a mathematics topic.
Early Number Work
Sorting/classifying
An important mathematical pre‐skill is the ability to differentiate objects and group together those with common attributes, such as colour, size or function. This activity is the first stage towards counting the objects in a set. Piaget emphasised the importance of classification, that is, the ability to sort objects according to a characteristic similarity such as size, colour or shape and seriation, the ability to arrange objects (and numbers) in increasing or decreasing size.
The number zero is an important concept to introduce, even at this early stage. It can be introduced here to represent the complete absence of any objects in the set (or group). This early exposure is important to introduce to a child in a clear way the concepts built around zero.
Correspondence between sets of objects
Understanding that two sets contain the same number of objects can be achieved by matching each object from the first set with each object from the second. If there are any objects left after such a matching process, then one set contains more objects and the other contains fewer objects.
This level of understanding allows sets of objects to be compared, even though the actual number in either set is established. This acts as an early introduction to the concept of ‘more than’ and ‘less than’ and to the question, ‘Is it bigger or smaller?’ The same approach can be extended to compare more than two sets and thus the idea of rank orders.
There are some benefits in using the patterns we use in this book, though they should not be used exclusively. The goal is to get the child to recognise a quantity with absolute consistency. They can also be used to compare two sets without using numbers, for example:

Correspondence between objects and numbers: counting
Stage 1
Introducing the number words and number symbols gives, in effect, abstract sets, which can be matched with sets of actual objects. For example, when the set of three objects is seen to correspond with the symbol ‘3’, we can begin to call the number of objects ‘three’.
It can then be seen that if the objects are counted in any different order, the correspondence shows that there are still three. Furthermore, if other sets of different objects are also seen to correspond with 3, then the relationship of a constant ‘three‐ness’ for the two ‘different’ sets can be developed. Another important move forward comes if the child can be encouraged to explore the arrangement of objects within a set to discover that the number is conserved even though the arrangement is different. In this way the child learns the interrelationship of numbers, for example 3 = 2 + 1 or 1 + 2 and then later 3 as 5 − 2 so that the interrelationships between key numbers, 1, 2, 5, 10 is an early experience.
Stage 2
At this stage the child is starting to relate the objects, the symbol for the number of objects, and the word (sight and sound) for the number, and the ‘break down’ of the number (Table 5.1).
Table 5.1 Tallies, symbols and words representing numbers.
| Objects |

|
|||||
|
Number symbols (Digits) |
1 | 2 | 3 | 4 | 5 | 6 |
|
Words (Sounds) |
one | two | three | four | five | six |
It is necessary for the number symbols and sounds in the above table to be known by heart. The exact spelling of the number words is of less importance (and likely less achievable) for children with dyslexia. The ARROW strategy (Lane, 1992; 2012) may well be of use to help achieve this target. ARROW is a multisensory learning and teaching approach developed in schools and researched under the auspices of Somerset County Council and the University of Exeter. ARROW uses a child’s own voice, the self‐voice, to develop skills central to reading, spelling, speaking and listening. ARROW is an acronym for Aural‐Read‐Respond‐Oral‐Written in which the self‐voice, replayed on audio‐CD or via a PC, is linked to looking, writing, listening and speech skills.
Stage 3
Counting can be used to associate the movement from object to object with a movement to the next number. In the early stages, while counting aloud, a child cannot always synchronise these movements and it may help if he counts against a regular rhythm or beat (e.g. a metronome).
This is also an introduction to addition.
Stage 4
The extension of the skill of counting forwards to the skill of counting backwards is not easy for the dyslexic or dyscalculic child. More practice in the reverse operation of removing one object at a time while counting the numbers backwards (and seeing the digits) will almost certainly be needed.
This is also an introduction to subtraction.
Stage 5
The Number Line (Figure 5.1) is useful at all levels of mathematics. Here it associates each extra mark with the next number and confers regularity and proportionality on the counting process. It also establishes the order of the numbers, as well as the convention for counting of increasing to the right and decreasing to the left. But beware. The converse is true for place value, another of the inconsistencies of early maths.
Furthermore, the regular spacing of the numbers begins the connection between numbers and length. This can be reinforced by using apparatus such as Dienes blocks or Cuisenaire rods. Cuisenaire rods are continuous, that is they do not have any gradations, so they give a different, but supportive perspective.
Number lines act as an intermediate stage between images of materials such as bead strings and Cuisenaire rods and symbols. Counting in both directions along the number line is beneficial for linking addition and subtraction.
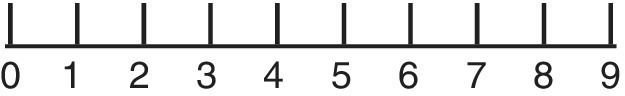
Figure 5.1 The number line.
Visual Sense of Number
Experiments can show that the visual sense of quantity (randomly arranged objects) is limited to about four or five. That is to say, most children will immediately recognise the number of objects in sets of one, two, three, four or five (without time for counting). This seems to imply that children have an in‐built ‘feel’ for the sizes or values of these numbers. Indeed some researchers believe the skill of realising a difference between one object and two objects exists in neonates.
From about six objects onwards, an accurate visual sense of number is less reliable and the objects have to be counted, unless there are other clues in the arrangement of the objects. In other words, the child has to use a one‐to‐one correspondence, treating each number as a separate identity. Thus he begins to relate numbers, build them up and see constituent parts.
Visual Clues to Number Concept
Numbers can more easily be ‘assessed and accessed’ if they form a recognisable pattern or if they can be seen as a combination of simpler numbers (this can be done in the early stages without a formal understanding of addition or multiplication). At this stage such an exercise adds further reinforcement to the idea of breaking down and building up numbers. The work can then be extended to bigger numbers, as shown in Figure 5.2. The numbers should become instantly recognisable through their patterns, familiar from dice and dominoes, though the authors are less happy with the pattern used on dice, dominoes and playing cards for six, that is two rows of three, rather than the 5 + 1 pattern advocated in this book for developing number sense.

Figure 5.2 Breaking down and building up numbers.
Any attempt to ‘standardise’ on a particular version is likely to be counterproductive, because each child will feel happiest with the version that suits him individually. Despite our principle that the best version is the one that works for a particular child, sometimes a little intrusion helps to rationalise and organise the child’s ideas, for example in guiding them towards use of the key numbers, 1, 2, 5 and 10.
Number Bonds/Combinations
The number bonds/combinations (for sums below ten) are fundamental in aiding number concept. The preceding work has built up to this formal presentation of number facts. Knowledge of the number bonds is also important when addition is tackled formally. There are therefore two important reasons why they should be understood and learned at this early stage. The following are likely to be the most useful:
| 2 as 1 and 1 | |||||||
| 3 as 2 and 1 | 1 and 2 | ||||||
| 4 as 3 and 1 | 2 and 2 | 3 and 1 | |||||
| 5 as 4 and 1 | 3 and 2 | 1 and 4 | |||||
| 6 as 5 and 1 | 4 and 2 | 3 and 3 | 2 and 4 | 1 and 5 | |||
| 7 as 6 and 1 | 5 and 2 | 4 and 3 | 3 and 4 | 2 and 5 | 1 and 6 | ||
| 8 as 7 and 1 | 6 and 2 | 5 and 3 | 4 and 4 | 3 and 5 | 2 and 6 | 1 and 7 | |
| 9 as 8 and 1 | 7 and 2 | 6 and 3 | 5 and 4 | 4 and 5 | 3 and 6 | 2 and 7 | 1 and 8 |
Consecutive columns give practice at adding 1, 2, 3, 4, 5, 6, 7 and 8 respectively, show a pattern in the combinations and illustrate the commutative property of addition.
Practice can, for example, be scheduled in the following ways:
- Adding 1 to each number from 1 to 8
- Adding every number from 2 to 7 to the number 2
- Adding the numbers randomly
- Adding numbers in every possible way to make a given sum, such as 7
The practice can be supported by using ‘concrete’ materials:
- Any form of counters that remain separate, so that the child sees the ‘ones’ in each part and the resultant whole, possibly arranged in recognisable patterns.
- Blocks, like centicubes, which can be joined together and separated, so that the child starts to see the numbers holistically.
- Cuisenaire rods, where each number is represented by a rod of different length and colour, so that the child visualises the ‘sizes’ of the numbers, rather than counting in ones. They are a ‘continuous’ material.
- A number line, which links the numbers to a sense of proportionality and sequencing and allows the child to track forwards and backwards.
An important consequence of this work should be the establishment of the commutative law, which states that the order in which the numbers are added does not affect the answer, in other words 2 + 5 = 5 + 2 = 7. This also reinforces what will be an important component of the developmental structure of our philosophy, that is, the learner is encouraged to look and consider before starting to compute. For example, in adding a small number such as 2 to 7, it is better to start with the 7 and count on the 2, than start with the 2 and count on 7. This does require teachers to ease back on the demand for instant answers or instant reactions.
You will need to establish the commutative law by reminding and organising the child to see the logic of the demonstrations he has just undertaken.
This latter concept, plus the actual number bonds/combinations is summarised below:

This table can be used for reference by the child and as a compact source from which to memorise the data. The patterns and sequences help the memorising.
Place Value
Number sense and place value understanding are found to be core numerical abilities for Chinese children learning early mathematics. Deficiencies in these two numerical skills, together with fact‐retrieval and procedural skills could predict Chinese children having difficulties learning mathematics in the first few school years (Ho et al., 2015). (See also Ho and Cheng, 1997.)
The use of base ten and the consequent place value of numbers are conventions that lie at the heart of our number system. The most frequent, and predictable, difficulty that occurs is that the child does not understand that the value of a digit depends on its place in a string of digits. This difficulty is not to be confused with the transposal of numbers (e.g. 34 for 43). There are also some problems with misunderstanding the language of these conventions. For example, a number such as ‘three hundred and fifteen thousand’ could be 30015000. Many problems that appear in later numeracy can be traced back to a lack of understanding of place value. It therefore needs careful attention, particularly when zeros are involved.
Grouping in tens
The number ten owes its significance to the number of fingers we have and their use in counting. This use of ten as a collective unit has significance in the written symbols we use for numbers. We have ten fingers and ten different number symbols. When we ran out of fingers for counting a quantity bigger than ten, we had to use something else, for example a second person's fingers, likewise when we ran out of number symbols we had to use a second, additional symbol. Using this in another column or place was a crucial concept in the history of mathematics.
The following approach attempts to show a logical connection between a number of objects and the symbols used to write the numbers. The approach moves from the concrete to the abstract, ‘foreign language’, written form in progressively more abstract/representative forms.
Step 1 Physically grouping
Objects do not naturally form themselves into groups of ten. Practice in doing this can be the first step towards understanding. The type of exercise here is simply to provide a group of items and let the child group them in tens, possibly as two groups of five. What the child sees are groups of tens which are numerically proportional to their value (Figure 5.3).

Figure 5.3 Physically grouping.
Step 2 Using base ten blocks
Dienes (or base ten) blocks have a different block for ten, which is in direct proportion to the length of ten ones blocks (Figure 5.4).
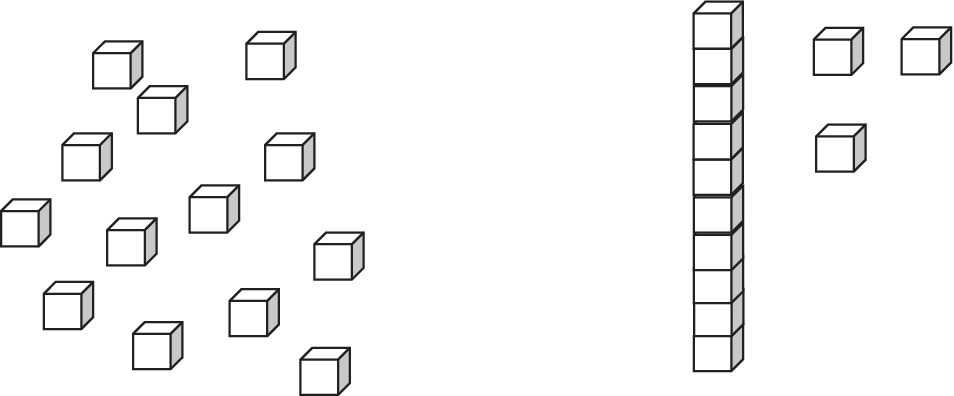
Figure 5.4 Base ten blocks.
Step 3 Using money
Although a 10p coin is physically larger than a 1p coin, it is not proportionally ten times bigger, but it is a different colour. The use of money therefore moves the child towards non‐proportional representation of quantity (Figure 5.5a).

5.5a Using money.
Step 4 Using written tally symbols
The use of different tally symbols for ten and one, such as used in ancient Egypt and for Roman numbers, gives a written symbol version of the money activity above (Figure 5.5b) and shows that grouping into tens has a long history.
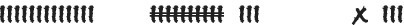
5.5b Using tally symbols.
Another suitable manipulative type of object here is bundles of ten cocktail sticks or straws and single cocktail sticks or straws. The material retains proportionality, but emphasises the ‘collecting together’ of ones into tens.
Step 5 Recording in words
Writing numbers down can be achieved using the words ‘Tens’ and ‘Ones’ as labels (Figure 5.6).
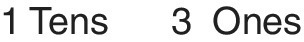
Figure 5.6 Recording in words.
Step 6 Using place value columns
Writing these labels for each number is inefficient and time consuming, but using them as headings (Figure 5.7) saves some of this effort, while leaving a clear reminder of the existence and value of the number places. Later we will use the place value cards to help maintain the concept during addition and subtraction.
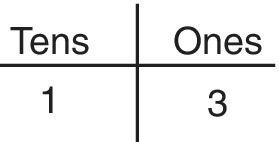
Figure 5.7 Using headings.
Step 7 Omission of the headings
Eventually, the headings can be dropped once their role in defining the place value of the digits is understood (Figure 5.8).

Figure 5.8 Omission of headings.
This is a highly structured progression and care must be taken before leaving any step out. It may be that the teacher simply moves through a particular step more quickly according to the learner’s response.
Tens alone
When we write 10, we are conveying that these two digits represents 1 ten and 0 ones. In some number systems, it would be redundant to mention the 0 ones, because zero means there are no objects there. The Hindu‐Arabic system use of zero is a very sophisticated concept. The Romans did not feel the need for a symbol for nothing. Place value uses fixed relative positions. So an understanding of the role of 0 as marking that a particular ‘place’ is empty is essential, as is its role of maintaining the place and thus value of the other digits. One good way of demonstrating this with children is to make each child a place value and his fingers the digits, so that 30 looks like Figure 5.9. The teacher can discuss with the children why the second (ones) child is needed to demonstrate 30.

Figure 5.9 Hands showing place value.
Figure 5.10 shows three ways of depicting four tens. They must be identified as tens, classified, counted and recorded together. The 0 in the written version 40 makes it quite clear that:
- The 4 objects are tens, and
- * There are no ones
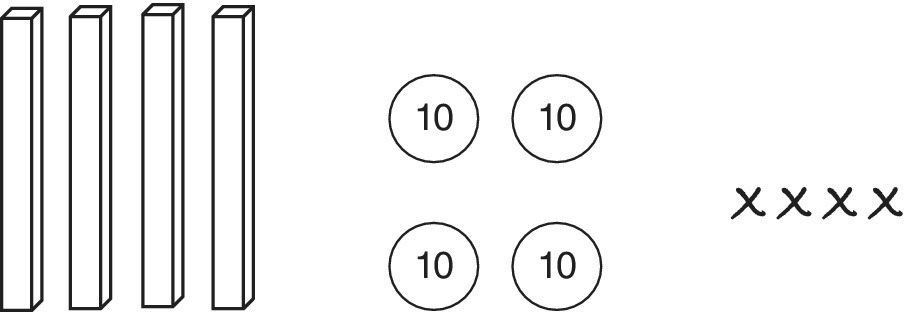
Figure 5.10 Three ways of depicting four tens.
In the spoken form, ten became abbreviated to ‐ty. Hence six tens became sixty, etc. Although it is obviously incorrect and contrived there is some good teaching value in the use of ‘tenty’ for one hundred. For example, it is a logical extension of the pattern of the other ‘‐ty’ numbers and helps the child realise something new is happening if we change the rule/pattern to a new word – hundred. It is also useful if renaming from the hundred column is used.
Grouping in hundreds
After 10, 20, 30, 40, 50, 60, 70, 80, 90, it is, if we understand the use of ten as the base number, impossible to record any more tens in the tens column. We have run out of number symbols again, using all the digits 1–9. If this counting in tens was demonstrated using 10p coins, there could also be an argument against having too many coins. The solutions to the two situations are parallel; we use another collective unit, hundred, in another column, or we use another coin. In each case, the hundred can be seen as 10 tens. Dienes blocks or cocktail sticks may again be used here, especially if the sticks are available in boxes of 100. In Figure 5.11 the number 235 is represented in various ways.

Figure 5.11 Representations of the number 235.
Grouping in thousands
Thousand is the next collective unit, composed of 10 hundreds. The next collective units are ten thousand and hundred thousand. The analogues of money, tally symbols and labels are less effective in contributing to an understanding of numbers above a thousand, although discussions about how many base ten thousand blocks would be needed to construct these higher value numbers are helpful, particularly as they continue to follow a pattern of ‘long’, ‘flat’ and ‘cube’. Usually, if place value has been properly understood up to this point, further extension of the system offers no further fundamental problems.
Certain large numbers with thousands can cause problems because of language, the word ‘ten’ used in ‘ten thousand’ and ‘hundred’ used in ‘hundred thousand’ and the large number of digits, many of which can be zeros. For example, the number two hundred and six thousand and fifty can be incorrectly written as 200600050, 2006050, 20600050, 2060050, 6250, etc. It can be helpful to consider the number in two parts: the thousands separate from the rest, which must fill three places (for hundreds, tens and ones) set aside in advance, for example for the above number the first step would be 206 □□□, then 206 □50, then 206 050.
Millions, billions and trillions
The collective units million, billion and trillion complete the picture. Million is the first new name after thousand. It is a thousand thousands. Again, consideration of the space occupied by a thousand ‘thousand’ blocks can help the concept. This volume is the space occupied by a metre cube. A billion is a thousand millions and a trillion is a thousand billions.
Some children can cope with exercises such as finding how high a pile of a million one pound coins would be or how far a billion millimetres would stretch. Ideas like this make useful investigations that can be used to develop concepts of large numbers.
It is worth noting that base ten blocks follow a repeating pattern in thousands: unit cube (a centimetre cube), long ten, flat hundred, thousand cube, (decimetre cube), long ten thousand, flat hundred thousand, million cube (one metre cube). This continues on again to one billion (a ten metre cube) and makes a good discussion topic. ‘How big is the billion cube? What object do you know that is about this size?’
Reminders and reviews
At any stage residual insecurity about a number can usually be addressed by the reintroduction of column headings.
The goal for the fundamental and vital concept of place value is automaticity. Reinforcement games such as:
Use the place value cards and ask the learner to collect a target number of coins, for example 56p. Dice are used to collect 1p coins which are placed in the ones column. When the ones column contains more than nine 1p coins then trading ten 1p coins for a 10p coin is used until the target is reached. The game then continues taking away 1p coins back to zero, using trading again, but now trading down from a 10p coin to ten 1p coins.
(It is possible to buy six‐sided dice with 1p, 2p, 5p, 10p, 20p, 50p and with 0, 1, 2, 5, 10, 20. See the Resources List.)
Diagnostic ideas
Questions such as the following can be used for practice, and for diagnosing difficulties:
- What is the value of the 7 in the number 4725?
- Write in figures thirty thousand and five.
- Write the numbers seventeen and then seventy‐one.
- Write in words 12,065.
- Write down the largest and smallest three‐digit numbers you can make with the three digits 2, 6 and 9.
Number Bonds/Combinations for Ten
Because of its universal significance, it is essential for a child to have a good understanding of ten (and its role in the base ten system). It is worth making a special study of the number bonds for ten and helping the child to learn these facts. They are core facts and, if rote learning a lot of facts is difficult, these are one of the key collections of facts that do need to be learned. Focus on learning the facts with the most value/mileage. There are several illustrations and exercises that can be used to help the child understand and visualise these facts.

All the different ways of making ten can be found, for example, by:
- Joining together ten centicubes, then breaking them up in various ways
- Using a ten‐bead bead‐string which is an excellent model for emphasising the conservation of 10 as the beads can’t get off, nor can any be added as it breaks down into different number bonds
- Laying down a Cuisenaire rod for ten, then laying down beside it combinations of other rods to give the same length
- Using an abacus
- Using coins or poker chip or chunky counters
- Using the pattern for ten

Diagrams like those in Figures 5.12 can help the memory.

Figure 5.12 Different font sizes to illustrate the number combinations for ten.
The number bonds/combinations for ten can be used and extended into many areas of numeracy, for example when adding a column of numbers by ‘casting out tens’ and the number bonds for 100. They are facts with high usage potential and thus worth a concentrated learning effort.
Numbers Near Ten, Hundred or Thousand
Ten, hundred and thousand are major ‘landmarks’ and reference points in the base ten system.
- From them, steps outwards can give meaning to numbers nearby, above or below. For example, the number 8 is just ‘less than’ 10, and the number 1010 is just ‘more than’ 1000. Later this can be quantified, as in 8 is 2 less than 10 and 1010 is 10 more than 1000.
- A question like 4 × 98 can be seen as just ‘less than’ 4 × 100. This can give the approximate answer ‘just below 400’, or can form the starting point for estimation work and mental calculations in the grasshopper style:
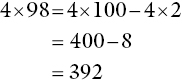
The appraisal question, ‘Is the answer bigger or smaller?’ can be used again in this context.
- Dienes/base ten blocks are designed to give visual, and kinaesthetic perspectives on these quantities and their relative values. It is not safe to assume that children will immediately make the relationship between blocks, symbols and quantities. You will have to demonstrate this.
- There are many examples of carefully chosen and presented visual images within the ‘Maths Explained’ video tutorials (www.mathsexplained.co.uk).
Summary
This chapter has looked at the concept of numbers and their values, concentrating on place value and the importance of key numbers, especially ten. The remaining chapters will continue to develop number concept and facility by extending the child’s experiences into the interrelationships of numbers and operations. What is important at this stage is that the child has some clear ideas as to the values of the low numbers, their relationship to the key numbers and an understanding of number bonds/combinations in the light of the conservation of number and the commutative law, and a clear concept of place value. This knowledge will form a sound base for the remaining development of maths skills and knowledge and thus the foundations for the developmental programme.
