17
Attacking and Checking Questions
Mathematics is an activity that has to be ‘performed’. A certain amount of theory must be committed to memory, but a pupil must be able to apply it to produce methodical solutions to questions asked. This will form the evidence that he is proficient in the subject.
It is now accepted that for dyslexics and dyscalculics the process of acquiring knowledge and understanding in mathematics should be structured to their particular needs and be multisensory. However, the provision of help with the application of the subject needs just as much thought. It would be hazardous at worst, and unproductive at best, to expect dyslexic and dyscalculic pupils to work it out for themselves without guidance and training.
This chapter is concerned with helping pupils cross the barrier between knowing the subject and successfully applying it.
The transitional stage of practicing must, especially in the first stages of practice, make sure the student is not developing incorrect procedures.
Practice Examples
For thorough understanding and preparation, a pupil needs to understand any topic ‘forwards, backwards, sideways, upside down and inside out’, because this is the way questions will be asked, for example:

For reasons such as lack of time and the pupils’ often limited concentration spans, it is probably not possible to cover all these viewpoints when first explaining an idea. Indeed this might actually confuse a pupil. The objective is to give valid, reliable and consistent information that can be picked up on later, as many times as is necessary, as the pupil encounters them again through practice examples.
There is a danger that should be recognised here. The number of questions a pupil completes for practice may be limited, for many reasons, such as lack of motivation or slowness in working. The consequence may be that he reaches only the earliest and the most straightforward examples in the exercises, never seeing the later, more searching questions. The result can be the worst of both worlds. If the simple questions are done correctly, he may think that he understands the topic totally, while the reality is that understanding is only superficial. Part of the teaching structure, the differentiation, for every topic should be a carefully chosen series of practice examples, which would not put all the questions that might enhance understanding at the end. One of the useful activities that maths department teachers and their learning support specialists can undertake is to create a resource of question sheets that have been selected to meet the needs of those students whose pace of work is slower, but whose potential level of achievement is high.
Although they are generally discussed separately in this chapter, attacking questions and checking them are interdependent processes, something best exemplified in the ‘trial and improvement’ methods, mentioned later. Indeed there are some checks that ought to be carried out before a question is attempted.
Preliminary Checks
- Recall/look up the relevant information/formula.
- Use the information given to check proposed/initial working.
- Make a rough estimate. If you can, a mental estimate will probably be the quickest.
1. Recall/look up the correct formula and then check it
Faced with a problem about a circle, many pupils remember the formula:
Unfortunately, they will go ahead and apply it even to questions involving the circumference of the circle, when they should use the (much less frequently remembered) formula:
Some pupils will find the area of a triangle by multiplying base × height. In fact, the answer obtained should then be halved. Since a triangle is not a rectangle it is sensible to assume that the formula for its area will be different to that for the rectangle.
One way to help ensure that the correct formula is chosen is to check its dimensions. Formulae for lengths must contain only one length, one dimension, for example, 4r for the circumference perimeter of a square. Note that because π is a constant, the formula for circumference, 2πr has only one dimension (one variable).
Because areas are two‐dimensional, formulae for areas must contain two lengths, two dimensions, multiplied together. For example, the area of a rectangle of sides a and b is given by A = ab, and the area of an ellipse by πab (again, because π is a constant this is still only two dimensions).
Because volumes are three‐dimensional, formulae for volumes must contain three lengths multiplied together. For example, the area of a cuboid of sides a, b and c is given by A = abc, and the volume of a cone by ⅓πr2h.
2. Use given information to check proposed/initial working
Example
Complete the following table for R = 3 V2 and then draw a curve with the values in the table:
| V | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| R | 0 | 75 |
In the question shown, by using core numbers, pupils should first ensure that:
- when V = 0 they can make the formula produce R = 0, and
- when V = 2 they can make the formula produce R = 12, and
- when V = 5 they can make the formula produce R = 75.
Then they can be confident that their method will be right for the values they have to work out and, therefore, that the graph will be correct.
3. Make a rough estimate first
Later, check that the exact answer is close to the rough estimate.
Example
For 12 × 145, we might estimate 10 × 150 = 1500.
We have decreased the 12 to 10, but roughly compensated by increasing the 145 to 150. This estimate could be done mentally by many pupils. Some examination questions explicitly test pupils’ ability to think this way, because this is often how we calculate in everyday life.
Attacking Questions
After the processes of understanding, learning and practising, there comes the point when maths has to be applied to problem questions, most significantly in test or examination situations. These will be different from practice situations in the level of pressure they bring and in the extraordinary wide variation in the questions that can appear, which rules out the possibility of rehearsing them all.
At this point, a structured approach is even more necessary than before. Dyslexic and dyscalculic students need to be taught the following:
- Not just to take a question at face value, for example in word problems don’t simply seek out an operation word, such as ‘fewer’ and assume the question can be solved correctly by a subtraction.
- How to examine a question, so as to enable the use of their preferred style of working, exploit their strengths and circumnavigate their weaknesses.
- How connections are made between the various techniques and items of knowledge needed for a question to be answered.
- How to draw some sort of illustration to help the comprehension as with the Singapore bar method (Kho et al., 2009).
The variety of approaches needed when attacking a question can be compared to guessing what a present is before you are allowed to unwrap it. You might (using most of your senses):
- Pick it up and feel its weight, squeeze it or shake it
- Turn it over
- Smell it
- Tap it to see what sound it makes
Methods of Attacking Questions
This section will describe a number of practical suggestions for ‘attacking questions’. The idea here is to give the pupil something to do to start. Starting is often the biggest hurdle. Pupils should carry out as many of the following steps as required:
- Use a refined estimate.
- Do not be afraid to take the long way round.
- Do what you are told by the question.
- Draw a diagram.
- Draw a graph.
- Try to interpret (decimal) numbers as money, which everybody understands better.
- Temporarily replace awkward numbers with easy numbers to clarify the method (then replace the actual numbers).
- In multipart questions, answer the later parts even if you cannot answer the earlier parts.
- When using a formula, consider whether you prefer to rearrange it before you substitute your values, or vice versa.
1. Use a refined estimate
After working out a rough estimate, we can often see ways of refining it to calculate the exact answer.
Example

Example
Find the cost of 24 square metres of carpet at £17.60 per square metre.
We might estimate by finding the cost of 25 square metres, because it is close and it is a quarter of 100 at £18 per square metre.
The accurate cost can be worked out by using 2 × 17.6 and 20 × 17.6

2. Do not be afraid to take the long way round
It is worth remembering that a long way is better than no way.
Example 1
Faced with a multiplication like the above, that is 12 × 145, if all else fails it is better to take a long way around than do nothing. It is legitimate to add 145, 12 times. It is highly undesirable to add 12, a 145 times. It is better to do those additions in easy chunks, for example 10 × 145 and 2 × 145.
Example 2
A division such as 5202 ÷ 17 would cause many (or even most) pupils to give up because they do not know the 17‐times table. In these circumstances, the repeated subtractions can be in ‘chunks’ of 17.
Set up some partial products or chunks to get the calculation started:


Set up an extra partial product:

Example 3
Even with a calculator, a longer way around can be beneficial. With a question such as:
it is possible to do the entire sum using the calculator and come out with a single, complete answer (=2.415). However, calculating the top and bottom separately and then putting them together is clearer and shows the working, which will earn marks in case of any errors. It also allows for generating an estimate for this intermediate step.
3. Do what you are told
Apart from the obvious need to avoid doing otherwise, sometimes following the instructions will lead pupils to places they would not have reached themselves.
Example
Complete this pattern, and find the answer for 26 × 16:
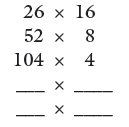
208 × 2 and then 416 × 1 complete the pattern.
Recognition that all the multiplications are equivalent shows that 26 × 16 = 416
Pupils will be led to the answer if they follow the given steps.
Some students would have given up at the beginning, because they think that they cannot work out the answer for 26 × 16.
4. Draw a diagram
If ‘a picture is worth a thousand words’, then there is an (almost) equivalent benefit to be gained in mathematics by using simple diagrams/drawings. The picture will give strong hints about how to move forwards. How many pupils would be stuck, or make errors such as 21 × 21 for the first example, if they drew the diagrams for the following two examples?
Example
What is the perimeter of a square whose side is 21 cm?

The likely mistake here is failure to realise we are talking about a square, although the word is there in the question. The act of drawing is likely to bring this into awareness. The danger of adding two sides instead of four is greatly reduced, as is the lure of multiplying the length by the width.
Example
What is the bearing of a ship travelling south‐east?
While a pupil might feel he knows what direction south‐east is, the picture (Figure 17.1) allows him to ensure that he is measuring ‘from the north, clockwise’, even if he does not use a protractor. It also gives him the reminder that his answer should be between 90° and 180°.

Figure 17.1 Bearing SE.
5. Draw a graph
A graph is another form of picture, of course.
For the effort expended on drawing and joining a few points on a graph, what is gained are all the points in between (an infinite number) and any points where the graph can be extended.
Example
Consider the problem of how to use 24 m of fencing in a rectangular shape to enclose the biggest possible area.
As the length increases (and the width decreases), the area changesone length + one width = 1/2 × perimeter = 1/2 × 24 = 12.
| Length | Width | Area |
| 1 | 11 | 11 |
| 2 | 10 | 20 |
| 3 | 9 | 27 |
| 4 | 8 | 32 |
| 5 | 7 | 35 |
| 6 | 6 | 36 |
| 7 | 5 | 35 |
| 8 | 4 | 32 |
| 9 | 3 | 27 |
| 10 | 2 | 20 |
| 11 | 1 | 11 |
From the table, it is evident that the biggest area is obtained with a square whose sides are 6 m, but consider the situation if we were forced to deal with decimal sides. In an examination, we might be asked to prove we have found the biggest arrangement. The graph of length against area are (Figure 17.2), especially with its symmetry, shows that no other value will give a greater area (even if the key decimal values are not calculated).

Figure 17.2 Graph for area versus length for rectangular shapes.
6. Try to interpret (decimal) numbers as money, which is usually understood better
Example
Put the following decimals in order, smallest first:
Pupils who do not fully understand place values will have the tendency to see 0.102 as bigger than 0.95, because ‘102 is bigger than 95’. Seeing the numbers as amounts of money can help, especially if they are lined up one below the other and zeros added to make them all three‐digit numbers:
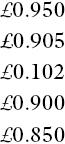
They can then recognise the correct order as:
7. Temporarily replace awkward numbers with easy numbers to clarify the method (then replace the actual numbers)
Given the problem:
many pupils would be put off by the numbers rather than by the concept.
If the problem is temporarily changed to:
then the method becomes obvious and the answer is clearly seen to be 80 ÷ 2, that is, 40 km/hour.
Pupils can now see that the distance must be divided by the time, and careful steps can now be taken to divide with the more awkward figures of the original problem.
8. In multi‐part questions, answer the later parts even if you cannot answer the earlier parts
Example
Using the following diagram
- Write down a formula for the area of the triangle
- Given that the area of the triangle is 35, show that
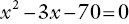
- Solve the equation


It may be impossible for pupils to write down the required formula for (a) or form the equation for part (b), but that need not prevent them from solving the more mechanical equation in (c) and earning the marks available for that part of the question.
9. When using a formula, consider whether you prefer to rearrange before you substitute your values, or vice versa
Example
Use the formula v = u + at, to find the value of a when v = 40, u = 30 and t = 5.
Rearranging the formula first:

Now substitute the numbers:
Checking
Pupils should recognise the need to check for mistakes, so it is important to emphasise how easily and frequently mistakes are made, and how costly they are. Left to their own devices, or, worse still, forced to check their work, many pupils will begin a desultory, and perhaps ill‐humoured, process of repeating their work. This is probably the least effective method of checking, and it is so boring that most will discontinue it, long before all their answers are checked.
Some mistakes are obvious and will stimulate an immediate check. Other errors are less obvious, but pupils should assume they are present, unless they can guarantee that all their work is always perfectly correct. There are many different kinds of mistakes that can be made, and there need to be just as many ways of checking for them. Some mistakes are random and can be corrected by repeating the same process, perhaps a little more carefully. Other mistakes are systematic and are caused by using incorrect procedures. To locate these takes more than just repetition.
Dyslexics and dyscalculics cannot be expected to work out how to do all this on their own. There is a need to structure the process or it will be confusing, tedious, ineffective and consequently omitted.
Methods of checking
- Ask, ‘Is the answer sensible?’
- Repeat the operations.
- Reverse the operations (work back from the answer).
- Use an entirely different method.
- Substitute the answer back into the question, especially if it is an equation.
- Some questions are self‐checking, for example pie charts.
1. Is the answer sensible?
Sometimes pupils are very confident about their answers, especially if they found the question easy to work out or were able to use a calculator. However, if they have worked out that a budgie weighs 10 tonnes, or that a car costs 34p, then they should be alert enough to see something is wrong.
2. Repeat the operations
Repeating the operations carries with it the risk of repeating errors made the first time, even with a calculator. Of course, some errors will be found, and this method is certainly better than not checking at all.
3. Reverse the operations
Example
To check a subtraction, we might add back the number subtracted.


4. Use an entirely different method
This ensures that none of the same errors will be made.
Example
A train journey begins at 10:20 and finishes at 12:05. How long does the journey take?
This could be calculated by subtracting the start time and the end time, remembering that time is not expressed in decimals (base ten), and that there are 60 minutes in an hour.
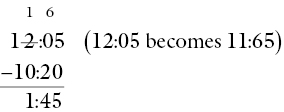
A completely different method could use a ‘time line’ (Figure 17.3).

Figure 17.3 A time line for “A train journey begins at 10:20 and finishes at 12:05”.
5. Substitute the answer back into the question, especially when using an equation
This method checks whether the answer really ‘works’.
Example
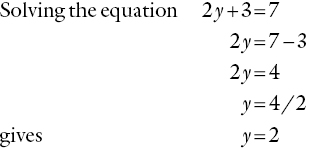
If y is really equal to 2, then the 2 should fit back into the equation instead of the y.
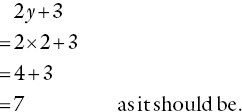
This idea forms the basis for iterative or ‘trial and improvement’ methods to solve equations. A first guess is made at the answer, perhaps from a hint in the question, and this is checked by substituting it back into the equation. This will not only identify a wrong guess, but it will indicate whether it is too big or too small, and possibly by how much.
Example
The equation 5x + 3 = 15 has a solution close to 2. Find the exact solution by trial and improvement.
Starting with a guess of 2 (from the estimate), the procedure is best set out in a table:
| Guess for x | Calculate 5x+3 | Should be 15 |
| 2 | 13 | Too small |
| 3 | 18 | Too big |
| 2.5 | 15.5 | Too big |
| 2.3 | 14.5 | Too small |
| 2.4 | 15 | Correct |
The correct answer is 2.4. Of course, it is possible to use a calculator to achieve an answer.
This method will be even more useful for harder quadratic and cubic equations.
6. Some questions are self‐checking
Example 1
Members of the public were asked to say which of the five TV channels, BBC1, BBC2, ITV1, Channel 4 and Channel 5 was their favourite. The responses are shown in the table.
Draw a pie chart to show the information in the table.
| Channel | Percentage | Angle |
| BBC 1 | 25 | 90 |
| BBC 2 | 10 | 36 |
| ITV 1 | 50 | 180 |
| Channel 4 | 10 | 36 |
| Channel 5 | 5 | 18 |
A pupil produced the pie chart in Figure 17.4.
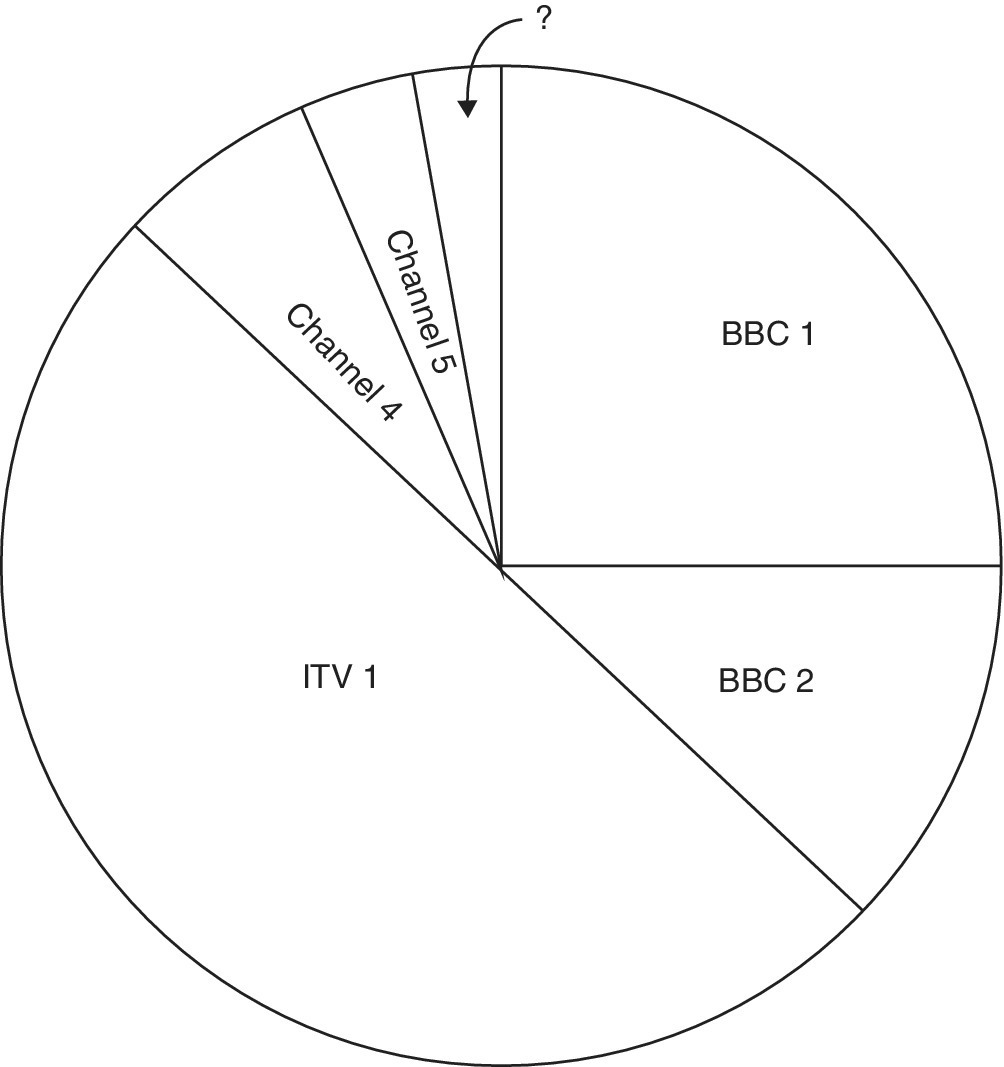
Figure 17.4 An inaccurate pie chart for the TV question.
Inaccurate drawing of the first four angles (slightly too small) implies that there was space left over after the Channel 5 sector. This is a signal that should not be ignored. For another pupil, drawing the angles slightly too big would leave insufficient space for the Channel 5 angle. Gross errors like using the percentage figure as the angle (e.g. 25 degrees for BBC1) would reveal a more dramatic amount of unused space, and should signal an error in the method.
Example 2
Using the example described earlier in the chapter, that is, requiring a curve to be drawn for R = 3 V2, if the points plotted do not form a perfect curve, then the error is with either the plotting or, more likely, the calculations. This should not be ignored, even for one point. It will be fairly easy to guess where the point should be, and correct the mistake accordingly.
