18
Important Elements of a Teaching Programme
Introduction
In this final chapter, it is our intention to show how we, as teachers and organisers, put our ideas into practice. If in many instances we seem to repeat what has been written earlier, this is because we regard it as sensible to take our own advice. However, we have avoided the repetition of examples at every point in order to reduce the amount of text, while attempting to make this chapter a useful summary of the whole book.
We hope that some of our ideas are applicable in all of the different environments where dyslexic and dyscalculic pupils are taught mathematics. However, it is the principal aim of this chapter to help in the complex situation where they are taught inclusively in classes with similar students, following a mainstream curriculum that is as normal as possible.
Consider the Pupils’ Needs
It is almost certain that the mathematical achievements of pupils diagnosed as dyslexic or dyscalculic will not match their potential. They may be from a wide range of backgrounds: social, economic and educational. In many cases, a child will present with significant problems in the affective domain. Although it is hard to prioritise interventions, the need to address anxieties, motivation and negative beliefs will be at least as important as intervention for cognitive development.
The curriculum should be directed towards creating a relaxed, encouraging, empathetic and low‐stress atmosphere, where children can take learning risks. When this is achieved, the pupils should start to feel confident that they can communicate their difficulties and have their questions answered sensitively. Setting up an ethos where the fear of negative evaluation is minimised is a worthy challenge.
The early stages of the course should provide work that is relatively easy, in order to restore a sense of success in pupils who may have experienced many failures, or indeed may have been labelled as failures. It is equally important that the work must not be perceived as too easy and patronising. It must be developmental and efficient if these vulnerable learners are not to fall further behind their peers. Catch‐up is another major challenge.
Pupils may have varying abilities and levels of achievement. There is not one common profile of difficulties. In their previous years of education, many will have survived by adopting idiosyncratic methods and/or an impressive range of avoidance strategies and may possess only a piecemeal understanding and knowledge of the subject. The aim is to build upon pupils’ strengths and extend what they do know and understand, trying to avoid imposing arbitrary changes, which will only add to their confusion. Teaching should provide the structure, pattern and organisation that their learning difficulty denies them and enable the full spectrum of learning styles to function and, it is hoped, broaden.
Against this background of intentions, it is crucial to maintain the rigour and integrity of the subject. Mathematics is a precise means of communication across the curriculum and in everyday life. It is important to resist the temptation to try and reduce it to a set of tricks. Even within the constraints of a national curriculum and the pressures for success in public examinations (and the PISA tables), it is possible to build a sound base for the further studies many pupils will pursue.
The Structure of the Course
In a world that would suit these learners, a structure based on a spiral with a small pitch allows regular revisits to the same topics (see Figure 18.1). This provides opportunities for essential over‐learning and acknowledges the difficulty in achieving mastery of some topics. A spiral with numeracy as its axis recognises the importance of numerical concepts as building blocks for the whole subject and as obstacles when they are not well understood. Topics should be changed frequently to promote and sustain interest. It is the objective that each topic is revisited before it has been forgotten. At each revisit, the topic is reviewed and then pushed to a slightly higher level, allowing for progress and giving time for ‘digestion’, but moving on before the pupil loses interest.
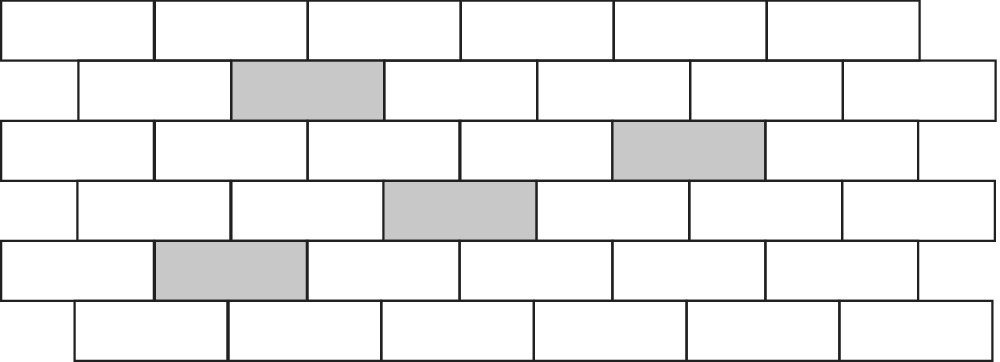
Figure 18.1 The missing bricks in the wall.
Numeracy
The vertical axis of the course begins with the following topics:
- Sorting and classifying
- Counting with whole numbers and using them to measure and draw
- Adding with whole numbers
- Subtracting with whole numbers
- Multiplying with whole numbers
- Dividing with whole numbers
- Understanding about parts of whole numbers
- The four operations for money
- The four operations for decimals
- The four operations for fractions
The axis of the spiral of progress is regarded as a continuum, rather than sets of skills to be acquired separately. The pupils’ own characteristic approaches are encouraged. For example, a pupil is encouraged to view a division such as 24 ÷ 4 as:
- A reverse multiplication, giving 6, because 6 × 4 = 24
- A repeated subtraction down to zero:

- Repeated subtraction in chunks:
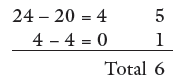
- Repeated additions up to the right answer:

Note that special attention should be given to the number facts for single‐digit addition, subtraction, multiplication and division, since knowing these facts, or having quick and reliable strategies with which to work them out, reduces the load on working and short‐term memories during calculations. This knowledge helps not only computation but also understanding of numbers.
General mathematical topics
Topics such as perimeter, area, equations, angle sums and graphs are introduced only when an appropriate level of numeracy has been reached. By using core numbers, this can be achieved relatively soon.
The mathematical variety needs to be as wide as possible as early as possible in order to maintain motivation and extend experience. It is particularly useful to introduce algebra very early, in the form of simple formulae at the conclusions of pieces of fully understood work. Algebra is a useful vehicle for developing the generalisation of skills, concepts and knowledge. For example, when working out a perimeter has been grasped for numbers, it is not a large conceptual leap for a pupil to understand that a + b + c is the formula or generalisation for the perimeter of a triangle with sides a, b and c.
Besides maintaining the students’ interest, dealing with a wide variety of topics has an even greater value in helping build foundations that are wide, so that difficult areas can be spanned just as missing bricks can be spanned in a wall (see Figure 18.1). Furthermore, relationships between mathematical topics are revealed and alternative paths are explored and developed. In this way, it becomes possible to put into practice the earlier claim to ‘build upon pupils’ strengths and extend what they do know and understand.
Using and applying mathematics
Investigational and practical work are sometimes viewed as ‘bolt‐ons’ to the curriculum when the student is struggling with the basics, but they are integral to the pupils’ understanding of the reasons for studying the subject and how it all works collectively. These activities help pupils with the organisation of their work and offer experiences with which to strengthen their concepts. Pupils usually respond with strong motivation for this alternative kind of work.
The use of patterns
The authors have long advocated the use of patterns in mathematics, as part of its structure. Patterns act as the mortar that holds the bricks of the subject together (Chinn and Ashcroft, 2004). We consider that patterns and their recognition can help in the following ways:
- Streamline and secure the learning of related facts
- Add interest and motivation (as puzzles and games can)
- Help with conceptual problems, by providing another way of looking at things
- Rationalise idiosyncrasies
- Provide structure
- Encourage generalisation skills
- Help long term memory
Mental arithmetic
Throughout the course, pupils should be encouraged and shown how to develop methods of calculating answers mentally, something most of us need to do in everyday situations. They should not be expected to create these methods by themselves, but any methods they have already adopted should be welcomed and discussed. Whether the expectation is for a correct answer or merely an estimate, pupils should be encouraged to use mental calculations as their first resort and then as their last resort when verifying or checking an answer.
However, the problems of weak short‐term and working memories are likely to make mental arithmetic very challenging. The pupil is likely to need appropriate differentiation if he is not to be seriously demotivated by this activity. One example of differentiation is to show the problem, for example, written on a white board, so that the pupil can at least focus on the computation.
Classroom Management: Making the Lessons Suit the Pupils
In general, the short attention spans and memory deficits of dyslexic pupils require that a lesson should be divided into short subsections, alternating exposition, demonstration, practical work, discussions, practice and so on. Also remember the saying,
‘Tell me and I will forget.
Show me and I will remember.
Involve me and I will understand.’
Perceptual and organisational difficulties dictate the need for clarity of presentation and thorough lesson preparation. Despite the work involved in the latter, there is also a seemingly opposing need for the teacher to be flexible enough to change direction in response to problems or opportunities as they present themselves during the course of a lesson. Hence the need to have a range of manipulative materials on hand for all lessons.
Board/screen work must be clear and uncluttered, preferably without too much information on display at any one time. Work should be presented both orally and visually. Memory overload must be avoided. Teachers should check that work is copied and copied correctly. Some pupils will need handouts.
Teachers should avoid talking (especially about important parts of the work) while the pupils are writing. A dyslexic pupil finds it hard enough to copy without this added distraction, which may be further compounded by worrying about what he is not hearing because he is trying to write. Dual tasking is not always a skill for this population.
Spread of ability
A teacher’s organisation and preparation should enable both faster and slower pupils to make progress. If he is devoting time to slower pupils, then faster pupils should have selected extra work to cover. Pupils can often learn well from each other, so faster pupils can sometimes be given the opportunity to develop their ‘communication level of understanding’ (Sharma, 1988), by helping slower pupils.
Pupils’ mathematical cognitive styles
Chapter 3 explains the two extremes of thinking style. Pupils will lie somewhere on this spectrum. At one extreme is the pupil described as an inchworm learner, who works part‐to‐whole, and at the other extreme is the pupil described as a grasshopper learner, who works whole‐to‐part. The inchworms follow a rigid, step‐by‐step, formula/algorithm‐based style when tackling mathematics. This is usually the way this type of learner is best taught. Conversely, grasshoppers work more intuitively and are very answer‐oriented. They may have been stifled and demotivated by being taught in the first style, to which many mathematics teachers arguably belong. A good mathematician needs to be flexible and make appropriate use of a mixture of the styles, so pupils need to be encouraged to consider more than one method when appropriate.
Pupils can be helped to find their own best way of working if the teacher:
- Begins each lesson with an overall picture of its contents, using both oral and visual stimuli
- Thoroughly explains the logic behind each method (as overview and then detail)
- Offers alternative methods
- Puts the work into a familiar context, or relates it to the pupils’ own experiences and existing knowledge
- Reviews the outcomes of the lesson
Evolving Expectations and Emphases
The nature of a pupil’s difficulties and his previous experiences in a classroom situation have often produced poor levels of achievement and an antipathy for the subject. It is essential to begin by taking the time to help the pupil rebuild confidence and develop a positive attitude. Create experiences of meaningful success for him. These successes, progressively gained, will lead the pupil to recognise his real abilities and raise his expectations, while equipping him with the knowledge and skills that will enable him to fulfil his true potential.
The initial aim of restoring pupils’ belief in their ability to succeed in mathematics is best met by building on what they already know, because they often know much more than they realise. Their knowledge just needs rationalisation and organisation. Much of the work should continue to cover the basics, in a manner that allows the teacher and pupils to:
- Revise important work
- Fill in as many gaps as possible
- Rationalise established ideas, which may be right, wrong, confused or inefficient
As confidence is developed, pupils’ attitudes will become more internalised, positive and motivated. The teacher should encourage the resulting acceleration.
Lesson management
To be taught in a whole class by an empathetic teacher offers some advantages over the individual help some dyslexic pupils receive. The members of the class should work together, share problems and accept mistakes, safe in the knowledge that few learners are perfect. They are encouraged to lose their fear of being wrong and thereby gain confidence. There should be a risk‐taking ethos in the classroom.
As pupils improve their mathematics at different paces, the differences between them will grow and become more evident. Each will have his own expectations and require these expectations to be met. Allowing and guiding them to work individually for some of the time encourages them to fulfil more of their potential. Class lessons may remain the main learning mode, but individual routes can be provided, where pupils choose from the following:
- Help or further practice with troublesome current work
- Revision of recent or seemingly mastered topics
- Extension work at higher levels
Published schemes, texts and carefully chosen work from the Internet are becoming increasingly valuable to support this way of working.
Teaching materials
A relevant teaching philosophy can be summarised simplistically as, ‘Mathematics is easy, only writing it down is hard’. Sometimes we explain by copying Figure 18.2 onto the board and ask pupils what they think it is.

Figure 18.2 ‘Is it a bike?’
Pupils will inevitably guess that it is a bike or a moped or a motorcycle or a scooter, and then become annoyed when this is refuted. It is possible to tease them even further by saying, ‘If it’s a bike, ride it down to the shop’. Eventually they are realise that we are showing something that it is not a bike, but a picture of a bike. In many ways, the mathematics we study is not real life, but only a written representation of a real problem. Sharing money between people is a real problem, which we can all do, while the usual written version of, for example, £12.48 ÷ 4 is just a picture, a theoretical version. If the written version can be shown to mimic the actual processes of dividing up the money, then more pupils will understand. This philosophy suggests the following sequence of steps:
- New topics are introduced through practical work, demonstrations, investigations, discussions and physical experiences. The use of a variety of these will facilitate the development and understanding of each concept. It can put them in a context.
- The next step is to try and translate the concept into a written form, linking the concrete experiences directly to the symbolic representation.
- This will lead into the use of worksheets or textbooks. The worksheets written and used by the authors start with worked examples, which are related to the earlier experiences. Then questions provide practice and revision. The worksheets are thus the third stage of the procedure and not the sole source from which the pupils are expected to learn.
Worksheets can follow a structured course and can be designed to enable the following:
- Present an advance overview of the section of work to be followed
- Eliminate the need for taking down notes, with its inherent risks of slow progress, mistakes, lack of clarity and readability
- Start at the most appropriate point
- Cover only a single concept, so that any point of difficulty can be readily identified, isolated and dealt with (that is, be diagnostic)
- Contain no more information than can be comfortably digested in one bite
- Present work clearly
- Use the fewest possible and simplest words, yet introduce the necessary technical terms carefully
- Incorporate exercises
- Provide a practical revision aid (used as ready‐made and organised notes)
- Carefully relate to other sheets
- Be designed to be criterion referenced, at least with some of the questions
As stated earlier, later on there will be a point when the differences between individual pupils begin to outweigh their similarities. Short worksheets, answered together at the same rate, are no longer ideal. At this point, it is also important for pupils to begin to use mainstream materials, as they must eventually face public examinations. An appropriate textbook or a series of textbooks, which becomes familiar and trusted, can provide help and reassurance, especially at the time of examinations. Textbooks provide different viewpoints and a variety in language, to which pupils must acclimatise when they are ready. The presentation of work in textbooks has become more and more appealing, with good graphics, uncluttered pages and well‐structured sets of examples. Textbooks must be chosen with great care, so as not to risk a reversal of the changes in attitude previously achieved. New approaches, as used in Singapore for example, are now being introduced.
Writing paper
If the responses of younger, newer pupils need more space than a worksheet allows, there are considerable benefits in using squared paper, either in loose form, to file with their worksheets, or in exercise book form. If centimetre squares are too large for many written answers, half‐centimetre (5 mm) squares offer invaluable help with:
- Lining up calculations vertically and horizontally
- Setting out tables and charts
- Doing measurements and diagrams, especially those in centimetres and/or using right angles
- Working out area problems
It is our view that dyslexic and dyscalculic pupils should be coached specifically through the transition from squared paper to lined (vertical lines can help with the alignment of calculations) and blank paper. The transition can take place when the value of the squared paper becomes outweighed by the need to prepare for public examinations, or at a time of the pupil’s choosing.
Calculators
With a course that initially has numeracy as its axis, the use of a calculator would be counterproductive. Unless there is another purpose to the work and it involves repetitive calculations, calculators should be discouraged at first.
Mental arithmetic is necessary for everyday life and for checking answers that are worked out using a calculator. Premature over‐reliance on a calculator could well delay the acquisition of these mental arithmetic skills, particularly estimation skills.
Furthermore, many of the later mathematical processes, such as (a + x)(b + y), are based on the early numerical processes, for example 35 × 24, which therefore need to be thoroughly understood.
There will be a point when pupils have learned all they can about manual calculations. Powerful calculators can be bought cheaply, but some have too many functions that will never be used and that make the machine difficult to operate. A simple solar‐powered calculator can be sufficient, with scientific functions, including fractions, percentages, and degrees/minutes/seconds, and which does not resort to scientific form in unnecessary cases.
A calculator is an ideal aid for the short‐term memory and can help compensate for a pupil’s remaining computational difficulties (which might only be a matter of speed). Logic and keying errors can be filtered out using checking methods (see Chapter 17). Specific calculator functions should be introduced on the basis of need, as with the trigonometric functions, for example. Specific time can be set aside for the exploration of other functions, such as n! (n factorial), which are of investigational interest.
Internal Assessment
Pupils need to be assessed regularly for the following purposes:
- Monitoring progress
- Diagnosis of difficulties
- Distinguishing mathematical cognitive style
Most dyslexic pupils will have a long history of ‘being tested’, but are usually reassured to be told that the results are for the above purposes only, and will have limited circulation. Ironically, yet usefully for examinations, the more the pupils are tested, the less they fear the process, which may be no more distasteful than any other mathematics lesson.
Monitoring progress
Standardised tests are called so because they have been given to a standard sample or population, before publication. The performance of any child can then be compared with this standard population. The results can be expressed in various ways.
Some tests produce a ‘mathematical age’, which can be compared with a child’s chronological age to give an idea of how far behind his attainment is in years and months. The results of subsequent repeat tests will show how much improvement has been made. This can be related to the time that has elapsed to give a ‘value‐added’ factor. For example, 18 months’ progress in a year could be defined as a value‐added factor of 1.5.
Some tests produce a mathematical ‘quotient’, which resembles IQ, and relates performance to an average figure of 100. For example, 96 is just below average, but within an average band.
Other tests produce a ‘centile’ or ‘percentile’ figure, which shows a child’s position in the standard population as a percentage. For example, a percentile figure of 20 would indicate that 20% of the population would be expected to perform at or below the child’s level.
Ideally, standardised tests should be repeated at similar times in the year for comparison purposes. Test results should be considered in conjunction with progress in class, and any other changes that may have occurred, to obtain a real picture of progress. Single test results should be treated with caution, as leaps in progress may not coincide with test dates. There is always the possibility that the test may have occurred on a bad day. Many pupils are labile in their performances.
Diagnosis of difficulties
Some tests are designed to assess mathematical sub‐skills separately, so that particular problem areas can be identified. The results can be used to direct subsequent teaching towards the areas of weakness. In an ideal classroom teaching and diagnosis should go hand‐in‐hand.
Pupils’ mathematical styles
The Test of Cognitive Style in Mathematics (Chinn, 2017a) can be used to determine mathematical learning/cognitive style. It distinguishes between the step‐by‐step ‘inchworm’ and the intuitive, holistic ‘grasshopper’. This test is for use with individual pupils and provides a measure of the pupil’s position on the continuum of styles from extreme inchworm to extreme grasshopper (see Chapter 3). It encourages discussion as to ‘How’.
Summary
Throughout all our years of experience teaching mathematics to dyslexics and dyscalculics, we have tried many things, filtered out what does not work and retained those ideas that have been successful. Therefore, the suggestions in this chapter and elsewhere in the book are included because they have worked for us. The application of the advice should be given careful thought, as other situations involving other factors may require different responses.
It has been our experience that the methods that work for dyslexic and dyscalculic pupils work for all pupils. This has implications for inclusion.
