10
Division: Whole Numbers
Introduction
In this chapter suggestions for teaching the concept of division, then division by single‐digit numbers and by powers of ten are discussed. For more complex divisions an alternative algorithm to the traditional one is discussed once again using core number partial products and interrelating the operations.
The ‘traditional’ procedure for long division is very demanding on many of the skill areas that dyslexic and dyscalculic students find most difficult. The algorithm traditionally used for long division requires good skills in sequencing, memory, knowledge of basic facts and spatial organisation. It is also difficult to model the logic of the traditional algorithm with manipulative materials.
Anghileri (1999) observes that: ‘There is now evidence that the procedural approach encouraged by the traditional algorithm leads pupils to ignore the meaning of the numbers as they try to remember complex procedures they have learned without really understanding.’ It is worth considering the problems dyslexic and dyscalculic learners face in this particularly challenging topic. The extent of these difficulties may be alleviated by referring back to, and building on, other work the student has covered and by interrelating concepts (such as subtraction and division) so as to try and make old and new work mutually supportive. Once again, the student’s existing knowledge makes a good baseline. So, you need to capitalise on this existing knowledge and thus should begin with informal diagnostic work, which is intended to find out what the student knows and which examples and illustrations he relates to.
The language of division can lead to early problems and can be an initial block to understanding of the concept and processes of division. A typical early question could be, ‘divide 36 by 6’ or ‘36 ÷ 6’. The order in which the numbers are stated in these two examples is the opposite to the demands of the traditional ‘bus stop’ algorithm, 6)36.
The instruction ‘divide’ might communicate better if it is used as ‘divide into n equal parts’ which links it more closely to ‘share equally between n people’. ‘Share’ is the better word to use for early, introductory work as it relates more readily to the manipulative materials and their everyday experiences.
The spatial and organisational demands of division algorithms are considerable. The traditional algorithm for 6)378 requires the child to work from left to right, writing the answer at the top, working from the hundreds to the tens and then to the ones and carrying down numbers as the problem proceeds. These requirements are almost directly opposite to those for the standard procedures for addition, subtraction and multiplication. Inconsistencies do not help, though, of course, they cannot always be avoided. Students can, however, be made aware of them.
Furthermore, to help meet these conflicting directional demands, the child may well need support in getting the digits into the correct place values on the answer line. Extra support for this accuracy can be provided by teaching estimating skills and by encouraging the child to overview the question (which may include rephrasing it.)
Introduction to Division
The initial aims are to introduce (or review) division in at least four ways: as sharing out or dividing up into parts; as finding out ‘how many numbers in’; as the converse of multiplication; as repeated subtraction. Each of these has a different vocabulary. An introductory activity of taking (small) numbers of counters and dividing them up into groups helps the child to see the processes of division in action and the interrelationship between division and subtraction. You can then extend the child’s perception of the activity by structured questions and representations of the ‘dividing up’ actions.
Example
Take 12 counters and place them randomly on a table (Figure 10.1). Ask the child to count them. (Some children will group the counters automatically when they do this.) Then ask the child to share/divide them into in three groups.
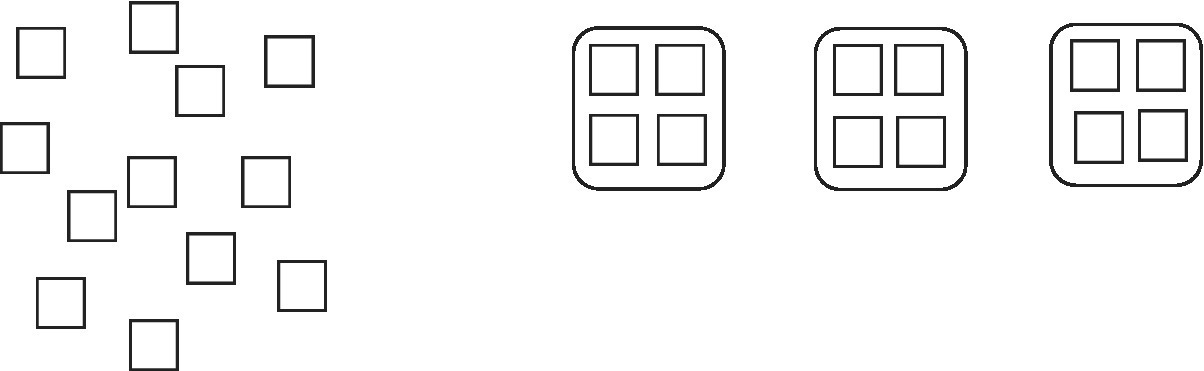
Figure 10.1 Showing twelve as three groups of four.
Ask the child to reorganise the groups into rows and columns. Then the following relationships can be examined as manipulatives and as equations. Again flexibility of language should help strengthen the concept:
Three lots of four (how many fours in twelve?).
Four lots of three (how many threes in twelve?).
Three goes into twelve four times.
Twelve divided by three gives four.
Repeated subtraction, three times, of four from twelve.
This work can be related back to the times table square. Its use as a division square can be taught.
Repeated subtraction relates division to subtraction and acts as a first exposure to a later algorithm. There are a number of ways ‘twelve divided by three’can be represented in symbols:
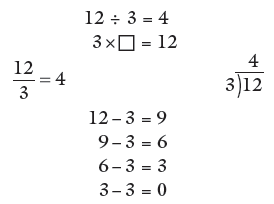
The child is being encouraged to see the relationship between division and multiplication, the idea of dividing up, the phrasing, ‘How many xs in y?’ as well as the concept of division as repeated subtraction and the idea of sharing equally. Simple division facts can be presented as multiplication facts with ‘gaps’ and the child can be shown how to use a table square to obtain division facts. Again, the child is being taught to use the interrelationships between numbers and operations in a way that makes maximum use of known facts, rather than rote learning seemingly unrelated facts.
Obviously many other examples besides 12 should be used, with the possibility of phasing out the multisensory manipulative aids as the child becomes more confident in his knowledge and understanding.
The relationship between the size/value of the divided number, divisor and answer can be shown by examples such as dividing 12 by a series of divisors: 12, 6, 4, 3, 2, 1.
| 12 ÷ 12 | = | 1 |
| 12 ÷ 6 | = | 2 |
| 12 ÷ 4 | = | 3 |
| 12 ÷ 3 | = | 4 |
| 12 ÷ 2 | = | 6 |
| 12 ÷ 1 | = | 12 |
Work of this type (using, as ever, written presentation alongside manipulative work) leads the child towards estimation skills. At the least, the child is learning that the bigger the divisor, the smaller the answer and the smaller the divisor the bigger the answer (setting the groundwork for division by numbers less than one). Once more the question, ‘Is the answer smaller or bigger?’ comes into play as the precursor to any calculation.
Dividing two‐digit numbers by one‐digit numbers, with remainder
Although the work described so far could be used to introduce a child to the topic of division, it is best considered as an early stage of intervention. For these early confidence‐building stages, remainders provide less confusion than decimal or fraction answers. Thus 14 ÷ 4 is presented with counters (Figure 10.2). It is apparent that the answer is 3 and that there are two counters left over or remaining. ‘Remainder’ seems to be a reasonable name for these counters.

Figure 10.2 Showing fourteen as four groups of three with two ‘left over’.
Dividing two and three‐digit numbers with renaming (of tens and hundreds)
Examples
65 ÷ 5
An efficient procedure for dividing 65 into five equal parts requires the student to progress from just counting out 65, sharing one by one, into five groups. He has to learn how to start with: ‘How many tens can I place in each of the five parts?’ then, ‘What do you do with the ten and the five ones left over from the 65?’ This is quite a leap in skill and understanding. The demands of the algorithm on areas of difficulty, for example organisation of work on paper and knowledge of division facts, are significant. Again, the teaching principle is to relate the symbols to the concrete and make the algorithm relate to a manipulative and then visual procedure. We advocate a structured approach that pre‐empts as many of the difficulties as possible and creates the concrete and visual images for the student:
- Sixty‐five is presented in base ten blocks (Figure 10.3a).
- Five tens are taken out, one to each of the five parts (Figure 10.3a).
- The ‘left over’ ten is traded for ten ones cubes and added to the existing five ones cubes.
- The fifteen ones cubes are shared out, adding three ones cubes to each of the five parts making 10 + 3, an answer of 13 (Figure 10.3b).
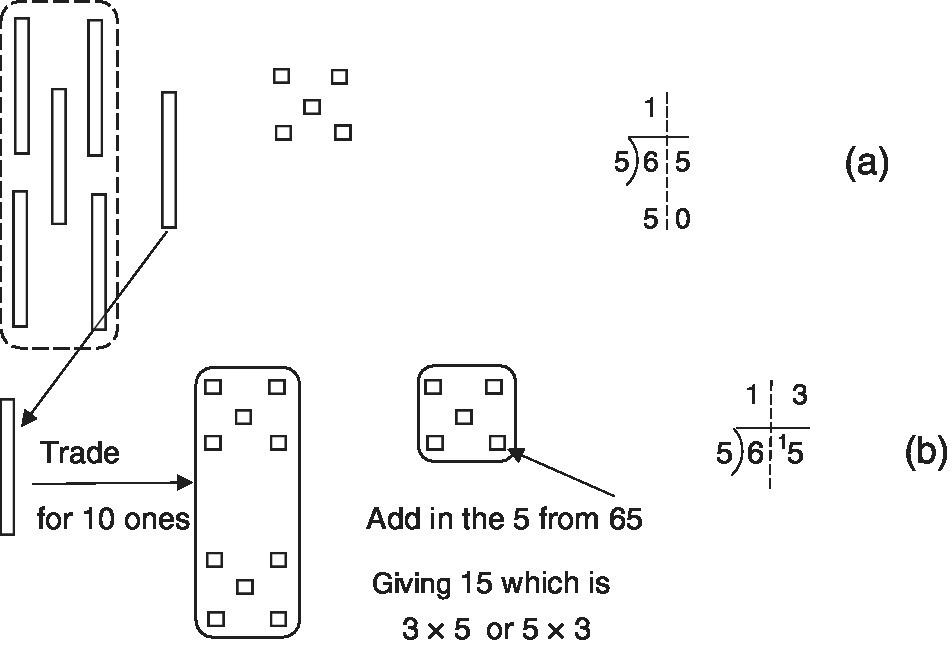
Figure 10.3 Using base ten blocks to demonstrate the division, 65 ÷ 5, as repeated subtraction.
At each stage the written algorithm matches the base ten manipulatives. You can explain the significance of each move and can relate it back to other work. For example, the need to trade tens for ones is used in this subtraction.
504 ÷ 4
- A similar structure is presented, with 504 shown in base ten blocks. This time the first move is to take out four hundreds blocks and place one in each part (Figure 10.4a).
- This leaves one hundreds block, which is traded for ten tens blocks, which are placed in the tens column. This highlights the previously empty tens column and emphasises the need to mark its presence in the answer line. Eight ten blocks are removed, two for each part (Figure 10.4b).
- The two remaining tens blocks are traded for ones cubes, giving twenty‐four ones cubes to share into the four parts, six in each (Figure 10.4c).
- The final answer is 126.

Figure 10.4 Using base ten blocks to demonstrate the division, 504 ÷ 4, as repeated subtraction.
Note the use of place value columns in the written version (given alongside the blocks in the parts of Figure 10.4). (Other suitable manipulative aids are money and bundles of cocktail sticks.)
Other examples should be used to consolidate this method. When the manipulative‐aid stage is phased out, the use of the place value columns should remain as these tends to eliminate the common errors of starting the answer in the wrong place or missing out a place as in 2)408 which is often erroneously answered as 24.
The principle is to share out the biggest place value equally, trade the left‐overs to the next place value down and share those equally, trading down again so that the procedure can be seen as a repeating steps.
Some alternative algorithms
Ashlock et al. (1983) offered two interesting alternatives, both based on repeated subtraction. Both require careful presentation. Chinn has adapted one of these algorithms to utilise the facts dyslexics can calculate readily, that is multiples of 1, 2, 5, 10, 20, 50, 100, etc., followed by repeated subtraction. The algorithm also fits into the developmental aspects of the programme. An example is shown in Figure 10.5.

Figure 10.5 Repeated subtraction of core number partial products.
Set up a table of key multiples (Figure 10.5a). These follow patterns, particularly for place value. An appraisal of thee multiples shows that the answer lies between 200 and 500. So, this procedure also provides an estimate. In this case since 5024 is nearer to 3200 than to 8000, the estimated answer must be closer to 200 than 500. Thus, the procedure encourages the pre‐evaluation of the answer, too.
The division is then tackled by subtraction of these multiples of 16 (Figure 10.5b). The method is related to our addition of partial products procedure advocated for multiplication, showing division to be the inverse operation and as repeated subtraction.
The authors’ experience of this method is that our 11‐year‐old learners can do this procedure with concrete materials (which act as an introduction to the method), but usually find the digits too difficult. By age 13 years the upper groups adapt to it readily. This method provides a good illustration of the ‘readiness’ of students (see ‘Time’) and the teacher should watch the class carefully to ensure understanding is achievable.
The student still has to be able to subtract. This remains a key prerequisite skill. There may well be more subtractions involved than in the traditional algorithm. It is the selection of the partial products that is made easier and less prone to error.
Estimating
The ability to multiply the divisor by powers of ten can be used to act as another useful and consistent estimating aid.
Example
1875 ÷ 15
The divisor is multiplied by increasing powers of ten and core numbers. The products are compared with 1875:
| 15 × 10 | = | 150 |
| 15 × 100 | = | 1500 |
| 15 × 200 | = | 3000 |
By comparing them to 1875, these products tell us that the answer will lie between 100 and 200, but closer to 100. Again, the link between division and multiplication is made and there is another chance for the child to reinforce his ability to multiply by powers of ten and the core numbers.
The ability to judge where the answer will lie is an extension of work with number lines, including empty number lines. It may well be beneficial to quickly revisit the skills associated with using these lines before attacking this new skill.
Division by Powers of Ten
This is the converse of setting up partial products for estimating. It requires an understanding of place value, so a review of this concept can be a precursor to the topic. The child needs to remember that the place a digit holds in a number controls its value by a power of ten (e.g. in 58725, the 7 is the third number in, it is in the hundreds column and its value is 7 × 100 or 700).
Division by powers of ten produces a pattern which can be illustrated by activities where the learner uses base ten blocks to divide numbers into ten parts and thus is drawn to the conclusion that, as with multiplying by powers of ten, the digits do not change, but their place value does change. At this early stage it is advisable to avoid answers that are decimals. A series of base ten block activities leads to series such as:
| 4000 ÷10 | = | 400 |
| 4000 ÷100 | = | 40 |
| 4000 ÷ 1000 | = | 4 |
| 4000 ÷ 10 | = | 400 |
| 4500 ÷ 10 | = | 450 |
| 4560 ÷ 10 | = | 456 |
It will almost certainly be necessary to use place value columns to emphasise the way the numbers move. A structured programme of manipulative aids (base ten blocks and/or money) and written digits should establish the idea of movement and values in the child’s mind and perhaps lead him to some mnemonics once the understanding is established. If this is so, then the move on to quotients that are decimals does not present such a difficult hurdle (see Chapters 11 and 13).
Division by Multiples of Powers of Ten
Examples such as 4000 ÷ 20, 3000 ÷ 2000, 4500 ÷ 50 can be solved by teaching the child to take a two‐stage approach: dividing first by 10 and then by 2; by 1000 then by 2; by 10 then by 5 respectively. This can be a multisensory activity with base ten blocks.
It also relates to the making of fractions such as ⅙ by a two‐stage process: ÷ 2 and ÷ 3 and back to times table strategies where 4× can be accessed by two stages as 2× and 2 × .
Conclusion
Further work may use calculators, providing that the student has an ability to estimate and check the answers. The work outlined in this chapter provides the student with the basic concept and the skills of division by subtraction of ‘chunks’ and the ability to estimate.
