In Chapter 4, Building Good Training Datasets – Data Preprocessing, you learned about the different approaches for reducing the dimensionality of a dataset using different feature selection techniques. An alternative approach to feature selection for dimensionality reduction is feature extraction. In this chapter, you will learn about three fundamental techniques that will help you to summarize the information content of a dataset by transforming it onto a new feature subspace of lower dimensionality than the original one. Data compression is an important topic in machine learning, and it helps us to store and analyze the increasing amounts of data that are produced and collected in the modern age of technology.

In this chapter, we will cover the following topics:

• Principal component analysis (PCA) for unsupervised data compression
• Linear discriminant analysis (LDA) as a supervised dimensionality reduction technique for maximizing class separability
• Nonlinear dimensionality reduction via kernel principal component analysis (KPCA)

Unsupervised dimensionality reduction via principal component analysis

Similar to feature selection, we can use different feature extraction techniques to reduce the number of features in a dataset. The difference between feature selection and feature extraction is that while we maintain the original features when we use feature selection algorithms, such as sequential backward selection, we use feature extraction to transform or project the data onto a new feature space.

In the context of dimensionality reduction, feature extraction can be understood as an approach to data compression with the goal of maintaining most of the relevant information. In practice, feature extraction is not only used to improve storage space or the computational efficiency of the learning algorithm, but can also improve the predictive performance by reducing the curse of dimensionality—especially if we are working with non-regularized models.

The main steps behind principal component analysis

In this section, we will discuss PCA, an unsupervised linear transformation technique that is widely used across different fields, most prominently for feature extraction and dimensionality reduction. Other popular applications of PCA include exploratory data analyses and the denoising of signals in stock market trading, and the analysis of genome data and gene expression levels in the field of bioinformatics.

PCA helps us to identify patterns in data based on the correlation between features. In a nutshell, PCA aims to find the directions of maximum variance in high-dimensional data and projects the data onto a new subspace with equal or fewer dimensions than the original one. The orthogonal axes (principal components) of the new subspace can be interpreted as the directions of maximum variance given the constraint that the new feature axes are orthogonal to each other, as illustrated in the following figure:

In the preceding figure, and are the original feature axes, and PC1 and PC2 are the principal components.

If we use PCA for dimensionality reduction, we construct a -dimensional transformation matrix, W, that allows us to map a vector, x, the features of a training example, onto a new k-dimensional feature subspace that has fewer dimensions than the original d-dimensional feature space. For instance, the process is as follows. Suppose we have a feature vector, x:

which is then transformed by a transformation matrix, :

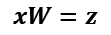
resulting in the output vector:

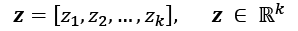
As a result of transforming the original d-dimensional data onto this new k-dimensional subspace (typically k << d), the first principal component will have the largest possible variance. All consequent principal components will have the largest variance given the constraint that these components are uncorrelated (orthogonal) to the other principal components—even if the input features are correlated, the resulting principal components will be mutually orthogonal (uncorrelated). Note that the PCA directions are highly sensitive to data scaling, and we need to standardize the features prior to PCA if the features were measured on different scales and we want to assign equal importance to all features.

Before looking at the PCA algorithm for dimensionality reduction in more detail, let's summarize the approach in a few simple steps:

1. Standardize the d-dimensional dataset.
2. Construct the covariance matrix.
3. Decompose the covariance matrix into its eigenvectors and eigenvalues.
4. Sort the eigenvalues by decreasing order to rank the corresponding eigenvectors.
5. Select k eigenvectors, which correspond to the k largest eigenvalues, where k is the dimensionality of the new feature subspace ().
6. Construct a projection matrix, W, from the "top" k eigenvectors.
7. Transform the d-dimensional input dataset, X, using the projection matrix, W, to obtain the new k-dimensional feature subspace.

In the following sections, we will perform a PCA step by step, using Python as a learning exercise. Then, we will see how to perform a PCA more conveniently using scikit-learn.

Extracting the principal components step by step

In this subsection, we will tackle the first four steps of a PCA:

1. Standardizing the data.
2. Constructing the covariance matrix.
3. Obtaining the eigenvalues and eigenvectors of the covariance matrix.
4. Sorting the eigenvalues by decreasing order to rank the eigenvectors.

First, we will start by loading the Wine dataset that we were working with in Chapter 4, Building Good Training Datasets – Data Preprocessing:

>>> import pandas as pd
>>> df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/'
...           'machine-learning-databases/wine/wine.data',
...           header=None)

df = pd.read_csv(
    'https://archive.ics.uci.edu/ml/'
    'machine-learning-databases/wine/wine.data',
    header=None)

df = pd.read_csv(
    'your/local/path/to/wine.data',
    header=None)

Next, we will process the Wine data into separate training and test datasets—using 70 percent and 30 percent of the data, respectively—and standardize it to unit variance:

>>> from sklearn.model_selection import train_test_split
>>> X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
>>> X_train, X_test, y_train, y_test = 
...     train_test_split(X, y, test_size=0.3,
...                      stratify=y,
...                      random_state=0)
>>> # standardize the features
>>> from sklearn.preprocessing import StandardScaler
>>> sc = StandardScaler()
>>> X_train_std = sc.fit_transform(X_train)
>>> X_test_std = sc.transform(X_test)

After completing the mandatory preprocessing by executing the preceding code, let's advance to the second step: constructing the covariance matrix. The symmetric -dimensional covariance matrix, where d is the number of dimensions in the dataset, stores the pairwise covariances between the different features. For example, the covariance between two features, and , on the population level can be calculated via the following equation:

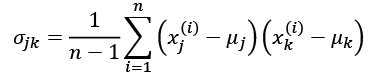
Here, and are the sample means of features j and k, respectively. Note that the sample means are zero if we standardized the dataset. A positive covariance between two features indicates that the features increase or decrease together, whereas a negative covariance indicates that the features vary in opposite directions. For example, the covariance matrix of three features can then be written as follows (note that stands for the Greek uppercase letter sigma, which is not to be confused with the summation symbol):

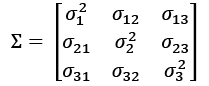
The eigenvectors of the covariance matrix represent the principal components (the directions of maximum variance), whereas the corresponding eigenvalues will define their magnitude. In the case of the Wine dataset, we would obtain 13 eigenvectors and eigenvalues from the -dimensional covariance matrix.

Now, for our third step, let's obtain the eigenpairs of the covariance matrix. As you will remember from our introductory linear algebra classes, an eigenvector, v, satisfies the following condition:

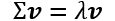
Here, is a scalar: the eigenvalue. Since the manual computation of eigenvectors and eigenvalues is a somewhat tedious and elaborate task, we will use the linalg.eig function from NumPy to obtain the eigenpairs of the Wine covariance matrix:

>>> import numpy as np
>>> cov_mat = np.cov(X_train_std.T)
>>> eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
>>> print('
Eigenvalues 
%s' % eigen_vals)
Eigenvalues
[ 4.84274532  2.41602459  1.54845825  0.96120438  0.84166161
  0.6620634   0.51828472  0.34650377  0.3131368   0.10754642
  0.21357215  0.15362835  0.1808613 ]

Using the numpy.cov function, we computed the covariance matrix of the standardized training dataset. Using the linalg.eig function, we performed the eigendecomposition, which yielded a vector (eigen_vals) consisting of 13 eigenvalues and the corresponding eigenvectors stored as columns in a -dimensional matrix (eigen_vecs).

Total and explained variance

Since we want to reduce the dimensionality of our dataset by compressing it onto a new feature subspace, we only select the subset of the eigenvectors (principal components) that contains most of the information (variance). The eigenvalues define the magnitude of the eigenvectors, so we have to sort the eigenvalues by decreasing magnitude; we are interested in the top k eigenvectors based on the values of their corresponding eigenvalues. But before we collect those k most informative eigenvectors, let's plot the variance explained ratios of the eigenvalues. The variance explained ratio of an eigenvalue, , is simply the fraction of an eigenvalue, , and the total sum of the eigenvalues:

Using the NumPy cumsum function, we can then calculate the cumulative sum of explained variances, which we will then plot via Matplotlib's step function:

>>> tot = sum(eigen_vals)
>>> var_exp = [(i / tot) for i in
...            sorted(eigen_vals, reverse=True)]
>>> cum_var_exp = np.cumsum(var_exp)
>>> import matplotlib.pyplot as plt
>>> plt.bar(range(1,14), var_exp, alpha=0.5, align='center',
...         label='Individual explained variance')
>>> plt.step(range(1,14), cum_var_exp, where='mid',
...          label='Cumulative explained variance')
>>> plt.ylabel('Explained variance ratio')
>>> plt.xlabel('Principal component index')
>>> plt.legend(loc='best')
>>> plt.tight_layout()
>>> plt.show()

The resulting plot indicates that the first principal component alone accounts for approximately 40 percent of the variance.

Also, we can see that the first two principal components combined explain almost 60 percent of the variance in the dataset:

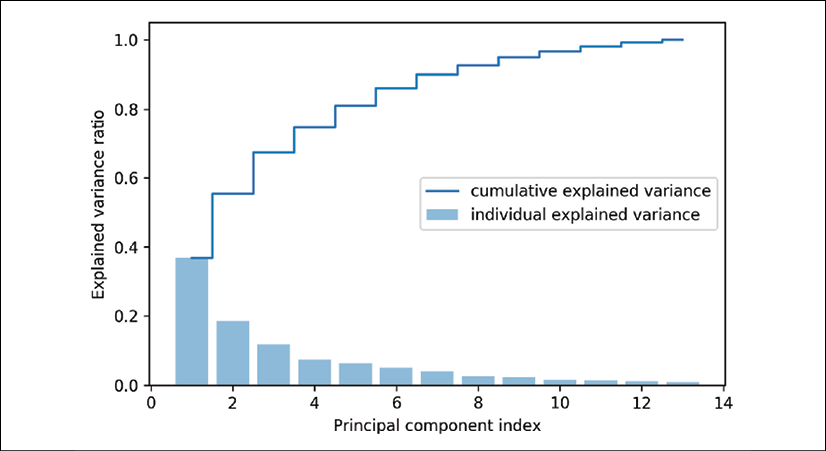
Although the explained variance plot reminds us of the feature importance values that we computed in Chapter 4, Building Good Training Datasets – Data Preprocessing, via random forests, we should remind ourselves that PCA is an unsupervised method, which means that information about the class labels is ignored. Whereas a random forest uses the class membership information to compute the node impurities, variance measures the spread of values along a feature axis.

Feature transformation

Now that we have successfully decomposed the covariance matrix into eigenpairs, let's proceed with the last three steps to transform the Wine dataset onto the new principal component axes. The remaining steps we are going to tackle in this section are the following:

5. Select k eigenvectors, which correspond to the k largest eigenvalues, where k is the dimensionality of the new feature subspace ().
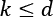6. Construct a projection matrix, W, from the "top" k eigenvectors.

7. Transform the d-dimensional input dataset, X, using the projection matrix, W, to obtain the new k-dimensional feature subspace.

Or, in less technical terms, we will sort the eigenpairs by descending order of the eigenvalues, construct a projection matrix from the selected eigenvectors, and use the projection matrix to transform the data onto the lower-dimensional subspace.

We start by sorting the eigenpairs by decreasing order of the eigenvalues:

>>> # Make a list of (eigenvalue, eigenvector) tuples
>>> eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
...                for i in range(len(eigen_vals))]
>>> # Sort the (eigenvalue, eigenvector) tuples from high to low
>>> eigen_pairs.sort(key=lambda k: k[0], reverse=True)

Next, we collect the two eigenvectors that correspond to the two largest eigenvalues, to capture about 60 percent of the variance in this dataset. Note that two eigenvectors have been chosen for the purpose of illustration, since we are going to plot the data via a two-dimensional scatter plot later in this subsection. In practice, the number of principal components has to be determined by a tradeoff between computational efficiency and the performance of the classifier:

>>> w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
...                eigen_pairs[1][1][:, np.newaxis]))
>>> print('Matrix W:
', w)
Matrix W:
[[-0.13724218   0.50303478]
 [ 0.24724326   0.16487119]
 [-0.02545159   0.24456476]
 [ 0.20694508  -0.11352904]
 [-0.15436582   0.28974518]
 [-0.39376952   0.05080104]
 [-0.41735106  -0.02287338]
 [ 0.30572896   0.09048885]
 [-0.30668347   0.00835233]
 [ 0.07554066   0.54977581]
 [-0.32613263  -0.20716433]
 [-0.36861022  -0.24902536]
 [-0.29669651   0.38022942]]

By executing the preceding code, we have created a -dimensional projection matrix, W, from the top two eigenvectors.

Mirrored projections

Depending on which versions of NumPy and LAPACK you are using, you may obtain the matrix, W, with its signs flipped. Please note that this is not an issue; if v is an eigenvector of a matrix, , we have:

Here, v is the eigenvector, and –v is also an eigenvector, which we can show as follows. Using basic algebra, we can multiply both sides of the equation by a scalar, :

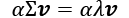
Since matrix multiplication is associative for scalar multiplication, we can then rearrange this to the following:

Now, we can see that is an eigenvector with the same eigenvalue, , for both and . Hence, both v and –v are eigenvectors.

Using the projection matrix, we can now transform an example, x (represented as a 13-dimensional row vector), onto the PCA subspace (the principal components one and two) obtaining , now a two-dimensional example vector consisting of two new features:

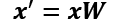
>>> X_train_std[0].dot(w)
array([ 2.38299011,  0.45458499])

Similarly, we can transform the entire -dimensional training dataset onto the two principal components by calculating the matrix dot product:

>>> X_train_pca = X_train_std.dot(w)

Lastly, let's visualize the transformed Wine training dataset, now stored as an -dimensional matrix, in a two-dimensional scatterplot:

>>> colors = ['r', 'b', 'g']
>>> markers = ['s', 'x', 'o']
>>> for l, c, m in zip(np.unique(y_train), colors, markers):
...     plt.scatter(X_train_pca[y_train==l, 0],
...                 X_train_pca[y_train==l, 1],
...                 c=c, label=l, marker=m)
>>> plt.xlabel('PC 1')
>>> plt.ylabel('PC 2')
>>> plt.legend(loc='lower left')
>>> plt.tight_layout()
>>> plt.show()

As we can see in the resulting plot, the data is more spread along the x-axis—the first principal component—than the second principal component (y-axis), which is consistent with the explained variance ratio plot that we created in the previous subsection. However, we can tell that a linear classifier will likely be able to separate the classes well:

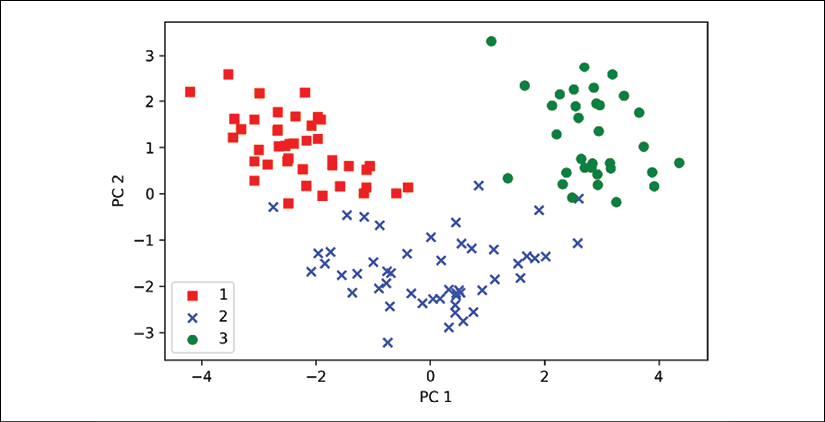
Although we encoded the class label information for the purpose of illustration in the preceding scatter plot, we have to keep in mind that PCA is an unsupervised technique that doesn't use any class label information.

Principal component analysis in scikit-learn

Although the verbose approach in the previous subsection helped us to follow the inner workings of PCA, we will now discuss how to use the PCA class implemented in scikit-learn.

The PCA class is another one of scikit-learn's transformer classes, where we first fit the model using the training data before we transform both the training data and the test dataset using the same model parameters. Now, let's use the PCA class from scikit-learn on the Wine training dataset, classify the transformed examples via logistic regression, and visualize the decision regions via the plot_decision_regions function that we defined in Chapter 2, Training Simple Machine Learning Algorithms for Classification:

from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
    
    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())
    
    # plot examples by class
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0],
                    y=X[y == cl, 1],
                    alpha=0.6,
                    color=cmap(idx),
                    edgecolor='black',
                    marker=markers[idx],
                    label=cl)

For your convenience, you can place the plot_decision_regions code shown above into a separate code file in your current working directory, for example, plot_decision_regions_script.py, and import it into your current Python session.

>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.decomposition import PCA
>>> # initializing the PCA transformer and
>>> # logistic regression estimator:
>>> pca = PCA(n_components=2)
>>> lr = LogisticRegression(multi_class='ovr',
...                         random_state=1,
...                         solver='lbfgs')
>>> # dimensionality reduction:
>>> X_train_pca = pca.fit_transform(X_train_std)
>>> X_test_pca = pca.transform(X_test_std)
>>> # fitting the logistic regression model on the reduced dataset:
>>> lr.fit(X_train_pca, y_train)
>>> plot_decision_regions(X_train_pca, y_train, classifier=lr)
>>> plt.xlabel('PC 1')
>>> plt.ylabel('PC 2')
>>> plt.legend(loc='lower left')
>>> plt.tight_layout()
>>> plt.show()

By executing the preceding code, we should now see the decision regions for the training data reduced to two principal component axes:

When we compare PCA projections via scikit-learn with our own PCA implementation, it can happen that the resulting plots are mirror images of each other. Note that this is not due to an error in either of those two implementations; the reason for this difference is that, depending on the eigensolver, eigenvectors can have either negative or positive signs.

Not that it matters, but we could simply revert the mirror image by multiplying the data by –1 if we wanted to; note that eigenvectors are typically scaled to unit length 1. For the sake of completeness, let's plot the decision regions of the logistic regression on the transformed test dataset to see if it can separate the classes well:

>>> plot_decision_regions(X_test_pca, y_test, classifier=lr)
>>> plt.xlabel('PC1')
>>> plt.ylabel('PC2')
>>> plt.legend(loc='lower left')
>>> plt.tight_layout()
>>> plt.show()

After we plot the decision regions for the test dataset by executing the preceding code, we can see that logistic regression performs quite well on this small two-dimensional feature subspace and only misclassifies a few examples in the test dataset:

If we are interested in the explained variance ratios of the different principal components, we can simply initialize the PCA class with the n_components parameter set to None, so all principal components are kept and the explained variance ratio can then be accessed via the explained_variance_ratio_ attribute:

>>> pca = PCA(n_components=None)
>>> X_train_pca = pca.fit_transform(X_train_std)
>>> pca.explained_variance_ratio_
array([ 0.36951469, 0.18434927, 0.11815159, 0.07334252,
        0.06422108, 0.05051724, 0.03954654, 0.02643918,
        0.02389319, 0.01629614, 0.01380021, 0.01172226,
        0.00820609])

Note that we set n_components=None when we initialized the PCA class so that it will return all principal components in a sorted order, instead of performing a dimensionality reduction.

Supervised data compression via linear discriminant analysis

LDA can be used as a technique for feature extraction to increase the computational efficiency and reduce the degree of overfitting due to the curse of dimensionality in non-regularized models. The general concept behind LDA is very similar to PCA, but whereas PCA attempts to find the orthogonal component axes of maximum variance in a dataset, the goal in LDA is to find the feature subspace that optimizes class separability. In the following sections, we will discuss the similarities between LDA and PCA in more detail and walk through the LDA approach step by step.

Principal component analysis versus linear discriminant analysis

Both PCA and LDA are linear transformation techniques that can be used to reduce the number of dimensions in a dataset; the former is an unsupervised algorithm, whereas the latter is supervised. Thus, we might think that LDA is a superior feature extraction technique for classification tasks compared to PCA. However, A.M. Martinez reported that preprocessing via PCA tends to result in better classification results in an image recognition task in certain cases, for instance, if each class consists of only a small number of examples (PCA Versus LDA, A. M. Martinez and A. C. Kak, IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(2): 228-233, 2001).

The following figure summarizes the concept of LDA for a two-class problem. Examples from class 1 are shown as circles, and examples from class 2 are shown as crosses:

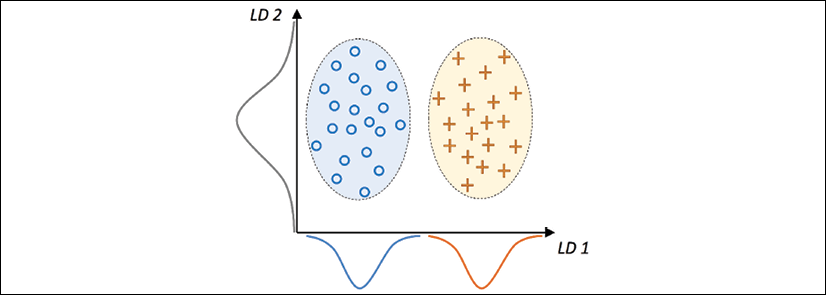
A linear discriminant, as shown on the x-axis (LD 1), would separate the two normal distributed classes well. Although the exemplary linear discriminant shown on the y-axis (LD 2) captures a lot of the variance in the dataset, it would fail as a good linear discriminant since it does not capture any of the class-discriminatory information.

One assumption in LDA is that the data is normally distributed. Also, we assume that the classes have identical covariance matrices and that the training examples are statistically independent of each other. However, even if one, or more, of those assumptions is (slightly) violated, LDA for dimensionality reduction can still work reasonably well (Pattern Classification 2nd Edition, R. O. Duda, P. E. Hart, and D. G. Stork, New York, 2001).

The inner workings of linear discriminant analysis

Before we dive into the code implementation, let's briefly summarize the main steps that are required to perform LDA:

1. Standardize the d-dimensional dataset (d is the number of features).
2. For each class, compute the d-dimensional mean vector.
3. Construct the between-class scatter matrix, 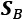, and the within-class scatter matrix, .
4. Compute the eigenvectors and corresponding eigenvalues of the matrix, .
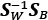5. Sort the eigenvalues by decreasing order to rank the corresponding eigenvectors.
6. Choose the k eigenvectors that correspond to the k largest eigenvalues to construct a -dimensional transformation matrix, W; the eigenvectors are the columns of this matrix.
7. Project the examples onto the new feature subspace using the transformation matrix, W.

As we can see, LDA is quite similar to PCA in the sense that we are decomposing matrices into eigenvalues and eigenvectors, which will form the new lower-dimensional feature space. However, as mentioned before, LDA takes class label information into account, which is represented in the form of the mean vectors computed in step 2. In the following sections, we will discuss these seven steps in more detail, accompanied by illustrative code implementations.

Computing the scatter matrices

Since we already standardized the features of the Wine dataset in the PCA section at the beginning of this chapter, we can skip the first step and proceed with the calculation of the mean vectors, which we will use to construct the within-class scatter matrix and between-class scatter matrix, respectively. Each mean vector, , stores the mean feature value, , with respect to the examples of class i:

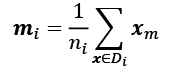
This results in three mean vectors:

>>> np.set_printoptions(precision=4)
>>> mean_vecs = []
>>> for label in range(1,4):
...     mean_vecs.append(np.mean(
...                X_train_std[y_train==label], axis=0))
...     print('MV %s: %s
' %(label, mean_vecs[label-1]))
MV 1: [ 0.9066  -0.3497  0.3201  -0.7189  0.5056  0.8807  0.9589  -0.5516
0.5416  0.2338  0.5897  0.6563  1.2075]
MV 2: [-0.8749  -0.2848  -0.3735  0.3157  -0.3848  -0.0433  0.0635  -0.0946
0.0703  -0.8286  0.3144  0.3608  -0.7253]
MV 3: [ 0.1992  0.866  0.1682  0.4148  -0.0451  -1.0286  -1.2876  0.8287
-0.7795  0.9649  -1.209  -1.3622  -0.4013]

Using the mean vectors, we can now compute the within-class scatter matrix, :

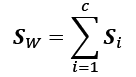
This is calculated by summing up the individual scatter matrices, , of each individual class i:

>>> d = 13 # number of features
>>> S_W = np.zeros((d, d))
>>> for label, mv in zip(range(1, 4), mean_vecs):
...     class_scatter = np.zeros((d, d))
>>> for row in X_train_std[y_train == label]:
...     row, mv = row.reshape(d, 1), mv.reshape(d, 1)
...     class_scatter += (row - mv).dot((row - mv).T)
...     S_W += class_scatter
>>> print('Within-class scatter matrix: %sx%s' % (
...       S_W.shape[0], S_W.shape[1]))
Within-class scatter matrix: 13x13

The assumption that we are making when we are computing the scatter matrices is that the class labels in the training dataset are uniformly distributed. However, if we print the number of class labels, we see that this assumption is violated:

>>> print('Class label distribution: %s'
...       % np.bincount(y_train)[1:])
Class label distribution: [41 50 33]

Thus, we want to scale the individual scatter matrices, , before we sum them up as scatter matrix . When we divide the scatter matrices by the number of class-examples, , we can see that computing the scatter matrix is in fact the same as computing the covariance matrix, —the covariance matrix is a normalized version of the scatter matrix:

The code for computing the scaled within-class scatter matrix is as follows:

>>> d = 13 # number of features
>>> S_W = np.zeros((d, d))
>>> for label,mv in zip(range(1, 4), mean_vecs):
...     class_scatter = np.cov(X_train_std[y_train==label].T)
...     S_W += class_scatter
>>> print('Scaled within-class scatter matrix: %sx%s'
...      % (S_W.shape[0], S_W.shape[1]))
Scaled within-class scatter matrix: 13x13

After we compute the scaled within-class scatter matrix (or covariance matrix), we can move on to the next step and compute the between-class scatter matrix :

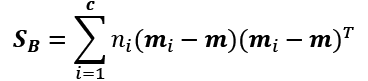
Here, m is the overall mean that is computed, including examples from all c classes:

>>> mean_overall = np.mean(X_train_std, axis=0)
>>> d = 13 # number of features
>>> S_B = np.zeros((d, d))
>>> for i, mean_vec in enumerate(mean_vecs):
...     n = X_train_std[y_train == i + 1, :].shape[0]
...     mean_vec = mean_vec.reshape(d, 1) # make column vector
...     mean_overall = mean_overall.reshape(d, 1)
...     S_B += n * (mean_vec - mean_overall).dot(
...     (mean_vec - mean_overall).T)
>>> print('Between-class scatter matrix: %sx%s' % (
...                S_B.shape[0], S_B.shape[1]))
Between-class scatter matrix: 13x13

Selecting linear discriminants for the new feature subspace

The remaining steps of the LDA are similar to the steps of the PCA. However, instead of performing the eigendecomposition on the covariance matrix, we solve the generalized eigenvalue problem of the matrix, :

>>> eigen_vals, eigen_vecs =
...     np.linalg.eig(np.linalg.inv(S_W).dot(S_B))

After we compute the eigenpairs, we can sort the eigenvalues in descending order:

>>> eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:,i])
...                for i in range(len(eigen_vals))]
>>> eigen_pairs = sorted(eigen_pairs,
...               key=lambda k: k[0], reverse=True)
>>> print('Eigenvalues in descending order:
')
>>> for eigen_val in eigen_pairs:
...     print(eigen_val[0])
Eigenvalues in descending order:
349.617808906
172.76152219
3.78531345125e-14
2.11739844822e-14
1.51646188942e-14
1.51646188942e-14
1.35795671405e-14
1.35795671405e-14
7.58776037165e-15
5.90603998447e-15
5.90603998447e-15
2.25644197857e-15
0.0

In LDA, the number of linear discriminants is at most c−1, where c is the number of class labels, since the in-between scatter matrix, , is the sum of c matrices with rank one or less. We can indeed see that we only have two nonzero eigenvalues (the eigenvalues 3-13 are not exactly zero, but this is due to the floating-point arithmetic in NumPy).

To measure how much of the class-discriminatory information is captured by the linear discriminants (eigenvectors), let's plot the linear discriminants by decreasing eigenvalues, similar to the explained variance plot that we created in the PCA section. For simplicity, we will call the content of class-discriminatory information discriminability:

>>> tot = sum(eigen_vals.real)
>>> discr = [(i / tot) for i in sorted(eigen_vals.real, reverse=True)]
>>> cum_discr = np.cumsum(discr)
>>> plt.bar(range(1, 14), discr, alpha=0.5, align='center',
...         label='Individual "discriminability"')
>>> plt.step(range(1, 14), cum_discr, where='mid',
...          label='Cumulative "discriminability"')
>>> plt.ylabel('"Discriminability" ratio')
>>> plt.xlabel('Linear Discriminants')
>>> plt.ylim([-0.1, 1.1])
>>> plt.legend(loc='best')
>>> plt.tight_layout()
>>> plt.show()

As we can see in the resulting figure, the first two linear discriminants alone capture 100 percent of the useful information in the Wine training dataset:

Let's now stack the two most discriminative eigenvector columns to create the transformation matrix, W:

>>> w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real,
...                eigen_pairs[1][1][:, np.newaxis].real))
>>> print('Matrix W:
', w)
Matrix W:
 [[-0.1481  -0.4092]
  [ 0.0908  -0.1577]
  [-0.0168  -0.3537]
  [ 0.1484   0.3223]
  [-0.0163  -0.0817]
  [ 0.1913   0.0842]
  [-0.7338   0.2823]
  [-0.075   -0.0102]
  [ 0.0018   0.0907]
  [ 0.294   -0.2152]
  [-0.0328   0.2747]
  [-0.3547  -0.0124]
  [-0.3915  -0.5958]]

Projecting examples onto the new feature space

Using the transformation matrix, W, that we created in the previous subsection, we can now transform the training dataset by multiplying the matrices:

>>> X_train_lda = X_train_std.dot(w)
>>> colors = ['r', 'b', 'g']
>>> markers = ['s', 'x', 'o']
>>> for l, c, m in zip(np.unique(y_train), colors, markers):
...     plt.scatter(X_train_lda[y_train==l, 0],
...                 X_train_lda[y_train==l, 1] * (-1),
...                 c=c, label=l, marker=m)
>>> plt.xlabel('LD 1')
>>> plt.ylabel('LD 2')
>>> plt.legend(loc='lower right')
>>> plt.tight_layout()
>>> plt.show()

As we can see in the resulting plot, the three Wine classes are now perfectly linearly separable in the new feature subspace:

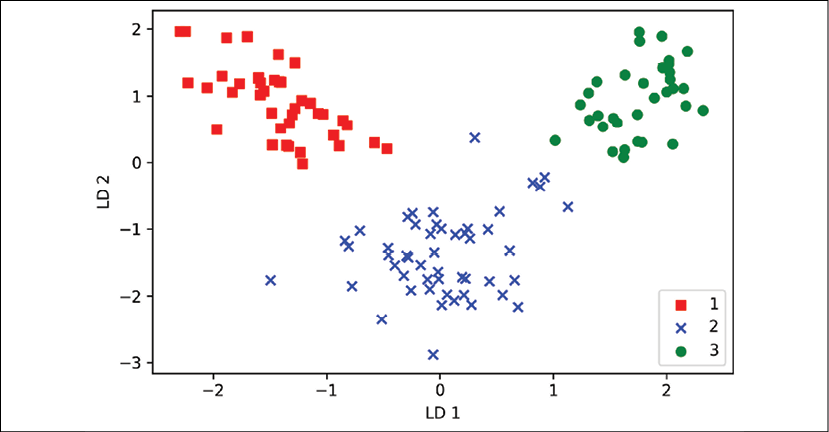
LDA via scikit-learn

That step-by-step implementation was a good exercise to understand the inner workings of an LDA and understand the differences between LDA and PCA. Now, let's look at the LDA class implemented in scikit-learn:

>>> # the following import statement is one line
>>> from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
>>> lda = LDA(n_components=2)
>>> X_train_lda = lda.fit_transform(X_train_std, y_train)

Next, let's see how the logistic regression classifier handles the lower-dimensional training dataset after the LDA transformation:

>>> lr = LogisticRegression(multi_class='ovr', random_state=1,
...                         solver='lbfgs')
>>> lr = lr.fit(X_train_lda, y_train)
>>> plot_decision_regions(X_train_lda, y_train, classifier=lr)
>>> plt.xlabel('LD 1')
>>> plt.ylabel('LD 2')
>>> plt.legend(loc='lower left')
>>> plt.tight_layout()
>>> plt.show()

Looking at the resulting plot, we can see that the logistic regression model misclassifies one of the examples from class 2:

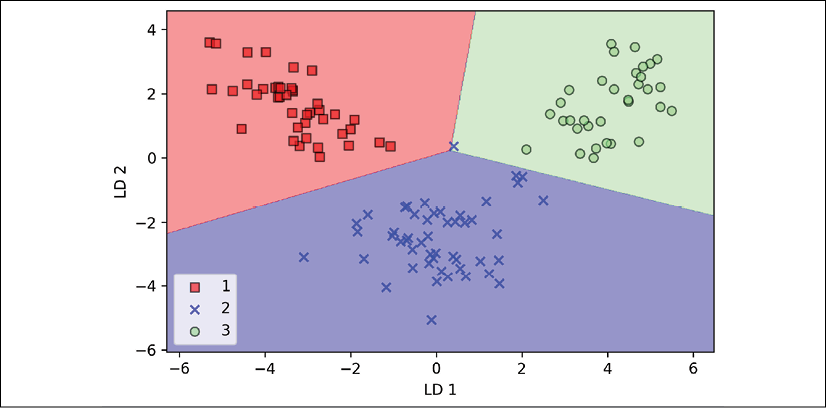
By lowering the regularization strength, we could probably shift the decision boundaries so that the logistic regression model classifies all examples in the training dataset correctly. However, and more importantly, let's take a look at the results on the test dataset:

>>> X_test_lda = lda.transform(X_test_std)
>>> plot_decision_regions(X_test_lda, y_test, classifier=lr)
>>> plt.xlabel('LD 1')
>>> plt.ylabel('LD 2')
>>> plt.legend(loc='lower left')
>>> plt.tight_layout()
>>> plt.show()

As we can see in the following plot, the logistic regression classifier is able to get a perfect accuracy score for classifying the examples in the test dataset by only using a two-dimensional feature subspace, instead of the original 13 Wine features:

Using kernel principal component analysis for nonlinear mappings

Many machine learning algorithms make assumptions about the linear separability of the input data. You have learned that the perceptron even requires perfectly linearly separable training data to converge. Other algorithms that we have covered so far assume that the lack of perfect linear separability is due to noise: Adaline, logistic regression, and the (standard) SVM to just name a few.

However, if we are dealing with nonlinear problems, which we may encounter rather frequently in real-world applications, linear transformation techniques for dimensionality reduction, such as PCA and LDA, may not be the best choice.

In this section, we will take a look at a kernelized version of PCA, or KPCA, which relates to the concepts of kernel SVM that you will remember from Chapter 3, A Tour of Machine Learning Classifiers Using scikit-learn. Using KPCA, we will learn how to transform data that is not linearly separable onto a new, lower-dimensional subspace that is suitable for linear classifiers.

Kernel functions and the kernel trick

As you will remember from our discussion about kernel SVMs in Chapter 3, A Tour of Machine Learning Classifiers Using scikit-learn, we can tackle nonlinear problems by projecting them onto a new feature space of higher dimensionality where the classes become linearly separable. To transform the examples onto this higher k-dimensional subspace, we defined a nonlinear mapping function, :

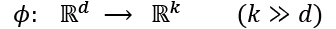
We can think of as a function that creates nonlinear combinations of the original features to map the original d-dimensional dataset onto a larger, k-dimensional feature space.

For example, if we had a feature vector (x is a column vector consisting of d features) with two dimensions (d = 2), a potential mapping onto a 3D-space could be:

In other words, we perform a nonlinear mapping via KPCA that transforms the data onto a higher-dimensional space. We then use standard PCA in this higher-dimensional space to project the data back onto a lower-dimensional space where the examples can be separated by a linear classifier (under the condition that the examples can be separated by density in the input space). However, one downside of this approach is that it is computationally very expensive, and this is where we use the kernel trick. Using the kernel trick, we can compute the similarity between two high-dimension feature vectors in the original feature space.

Before we proceed with more details about the kernel trick to tackle this computationally expensive problem, let's think back to the standard PCA approach that we implemented at the beginning of this chapter. We computed the covariance between two features, k and j, as follows:

Since the standardizing of features centers them at mean zero, for instance, and , we can simplify this equation as follows:

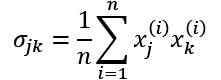
Note that the preceding equation refers to the covariance between two features; now, let's write the general equation to calculate the covariance matrix, :

Bernhard Scholkopf generalized this approach (Kernel principal component analysis, B. Scholkopf, A. Smola, and K.R. Muller, pages 583-588, 1997) so that we can replace the dot products between examples in the original feature space with the nonlinear feature combinations via :

To obtain the eigenvectors—the principal components—from this covariance matrix, we have to solve the following equation:

Here, and v are the eigenvalues and eigenvectors of the covariance matrix, , and a can be obtained by extracting the eigenvectors of the kernel (similarity) matrix, K, as you will see in the following paragraphs.

Deriving the kernel matrix

The derivation of the kernel matrix can be shown as follows. First, let's write the covariance matrix as in matrix notation, where is an -dimensional matrix:

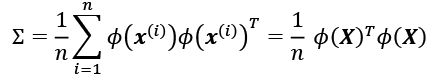
Now, we can write the eigenvector equation as follows:

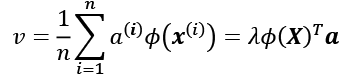
Since , we get:

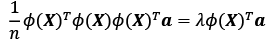
Multiplying it by on both sides yields the following result:

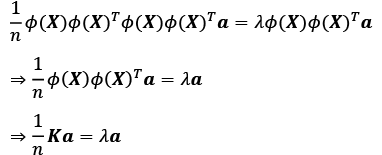
Here, K is the similarity (kernel) matrix:

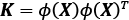
As you might recall from the Solving nonlinear problems using a kernel SVM section in Chapter 3, A Tour of Machine Learning Classifiers Using scikit-learn, we use the kernel trick to avoid calculating the pairwise dot products of the examples, x, under explicitly by using a kernel function, , so that we don't need to calculate the eigenvectors explicitly:

In other words, what we obtain after KPCA are the examples already projected onto the respective components, rather than constructing a transformation matrix as in the standard PCA approach. Basically, the kernel function (or simply kernel) can be understood as a function that calculates a dot product between two vectors—a measure of similarity.

The most commonly used kernels are as follows:

• The polynomial kernel:

  

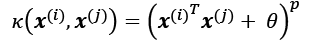
  Here, is the threshold and p is the power that has to be specified by the user.

• The hyperbolic tangent (sigmoid) kernel:

  

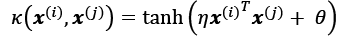
• The radial basis function (RBF) or Gaussian kernel, which we will use in the following examples in the next subsection:

  

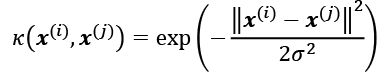
  It is often written in the following form, introducing the variable .

  

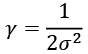To summarize what we have learned so far, we can define the following three steps to implement an RBF KPCA:

1. We compute the kernel (similarity) matrix, K, where we need to calculate the following:

   

   We do this for each pair of examples:

   

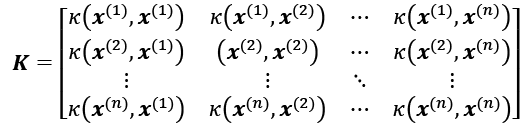
   For example, if our dataset contains 100 training examples, the symmetric kernel matrix of the pairwise similarities would be -dimensional.

2. We center the kernel matrix, K, using the following equation:

   

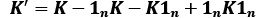
   Here, 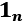is an 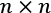-dimensional matrix (the same dimensions as the kernel matrix) where all values are equal to .

3. We collect the top k eigenvectors of the centered kernel matrix based on their corresponding eigenvalues, which are ranked by decreasing magnitude. In contrast to standard PCA, the eigenvectors are not the principal component axes, but the examples already projected onto these axes.

At this point, you may be wondering why we need to center the kernel matrix in the second step. We previously assumed that we are working with standardized data, where all features have mean zero when we formulate the covariance matrix and replace the dot-products with the nonlinear feature combinations via . Thus, the centering of the kernel matrix in the second step becomes necessary, since we do not compute the new feature space explicitly so that we cannot guarantee that the new feature space is also centered at zero.

In the next section, we will put those three steps into action by implementing a KPCA in Python.

Implementing a kernel principal component analysis in Python

In the previous subsection, we discussed the core concepts behind KPCA. Now, we are going to implement an RBF KPCA in Python following the three steps that summarized the KPCA approach. Using some SciPy and NumPy helper functions, we will see that implementing a KPCA is actually really simple:

from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
    """
    RBF kernel PCA implementation.
    
    Parameters
    ------------
    X: {NumPy ndarray}, shape = [n_examples, n_features]
    
    gamma: float
        Tuning parameter of the RBF kernel
    
    n_components: int
        Number of principal components to return
    
    Returns
    ------------
    X_pc: {NumPy ndarray}, shape = [n_examples, k_features]
        Projected dataset
    
    """
    # Calculate pairwise squared Euclidean distances
    # in the MxN dimensional dataset.
    sq_dists = pdist(X, 'sqeuclidean')
    
    # Convert pairwise distances into a square matrix.
    mat_sq_dists = squareform(sq_dists)
    
    # Compute the symmetric kernel matrix.
    K = exp(-gamma * mat_sq_dists)
    
    # Center the kernel matrix.
    N = K.shape[0]
    one_n = np.ones((N,N)) / N
    K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
    
    # Obtaining eigenpairs from the centered kernel matrix
    # scipy.linalg.eigh returns them in ascending order
    eigvals, eigvecs = eigh(K)
    eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
    
    # Collect the top k eigenvectors (projected examples)
    X_pc = np.column_stack([eigvecs[:, i]
                           for i in range(n_components)])
    
    return X_pc

One downside of using an RBF KPCA for dimensionality reduction is that we have to specify the parameter a priori. Finding an appropriate value for requires experimentation and is best done using algorithms for parameter tuning, for example, performing a grid search, which we will discuss in more detail in Chapter 6, Learning Best Practices for Model Evaluation and Hyperparameter Tuning.

Example 1 – separating half-moon shapes

Now, let us apply our rbf_kernel_pca on some nonlinear example datasets. We will start by creating a two-dimensional dataset of 100 example points representing two half-moon shapes:

>>> from sklearn.datasets import make_moons
>>> X, y = make_moons(n_samples=100, random_state=123)
>>> plt.scatter(X[y==0, 0], X[y==0, 1],
...             color='red', marker='^', alpha=0.5)
>>> plt.scatter(X[y==1, 0], X[y==1, 1],
...             color='blue', marker='o', alpha=0.5)
>>> plt.tight_layout()
>>> plt.show()

For the purposes of illustration, the half-moon of triangle symbols will represent one class, and the half-moon depicted by the circle symbols will represent the examples from another class:

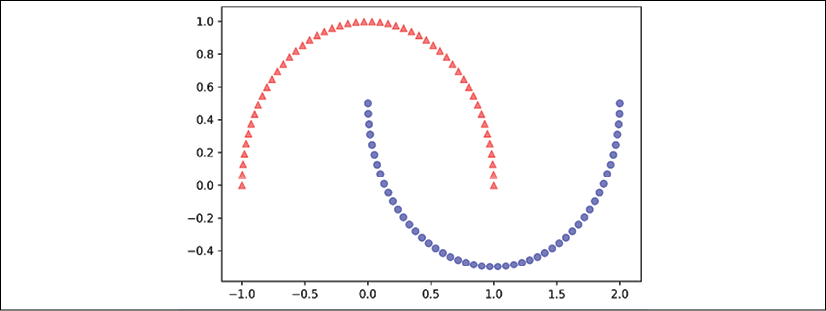
Clearly, these two half-moon shapes are not linearly separable, and our goal is to unfold the half-moons via KPCA so that the dataset can serve as a suitable input for a linear classifier. But first, let's see how the dataset looks if we project it onto the principal components via standard PCA:

>>> from sklearn.decomposition import PCA
>>> scikit_pca = PCA(n_components=2)
>>> X_spca = scikit_pca.fit_transform(X)
>>> fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7,3))
>>> ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1],
...               color='red', marker='^', alpha=0.5)
>>> ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1],
...               color='blue', marker='o', alpha=0.5)
>>> ax[1].scatter(X_spca[y==0, 0], np.zeros((50,1))+0.02,
...               color='red', marker='^', alpha=0.5)
>>> ax[1].scatter(X_spca[y==1, 0], np.zeros((50,1))-0.02,
...               color='blue', marker='o', alpha=0.5)
>>> ax[0].set_xlabel('PC1')
>>> ax[0].set_ylabel('PC2')
>>> ax[1].set_ylim([-1, 1])
>>> ax[1].set_yticks([])
>>> ax[1].set_xlabel('PC1')
>>> plt.tight_layout()
>>> plt.show()

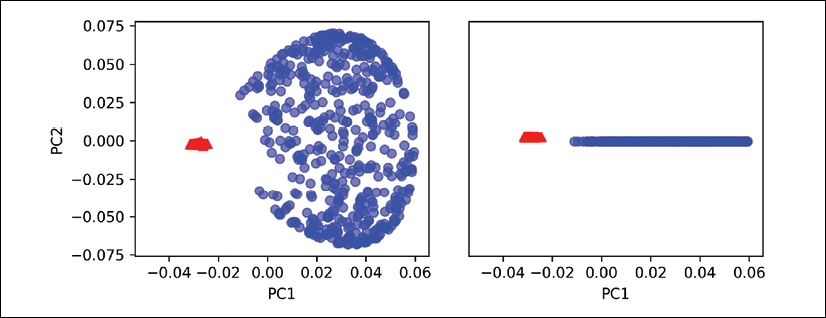
Clearly, we can see in the resulting figure that a linear classifier would be unable to perform well on the dataset transformed via standard PCA:

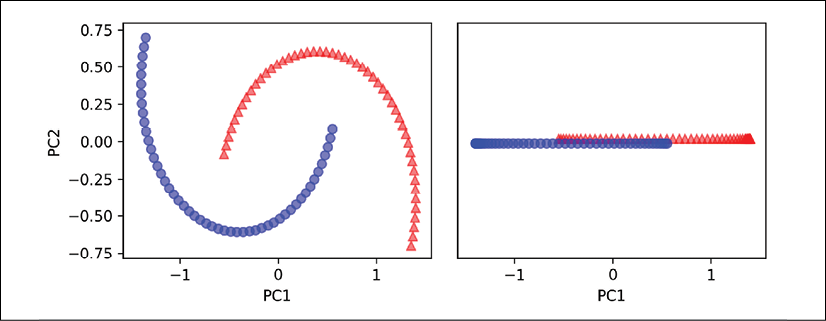
Note that when we plotted the first principal component only (right subplot), we shifted the triangular examples slightly upward and the circular examples slightly downward to better visualize the class overlap. As the left subplot shows, the original half-moon shapes are only slightly sheared and flipped across the vertical center—this transformation would not help a linear classifier in discriminating between circles and triangles. Similarly, the circles and triangles corresponding to the two half-moon shapes are not linearly separable if we project the dataset onto a one-dimensional feature axis, as shown in the right subplot.

Now, let's try out our kernel PCA function, rbf_kernel_pca, which we implemented in the previous subsection:

>>> X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
>>> fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
>>> ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
...               color='red', marker='^', alpha=0.5)
>>> ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
...               color='blue', marker='o', alpha=0.5)
>>> ax[1].scatter(X_kpca[y==0, 0], np.zeros((50,1))+0.02,
...               color='red', marker='^', alpha=0.5)
>>> ax[1].scatter(X_kpca[y==1, 0], np.zeros((50,1))-0.02,
...               color='blue', marker='o', alpha=0.5)
>>> ax[0].set_xlabel('PC1')
>>> ax[0].set_ylabel('PC2')
>>> ax[1].set_ylim([-1, 1])
>>> ax[1].set_yticks([])
>>> ax[1].set_xlabel('PC1')
>>> plt.tight_layout()
>>> plt.show()

We can now see that the two classes (circles and triangles) are linearly well separated so that we have a suitable training dataset for linear classifiers:

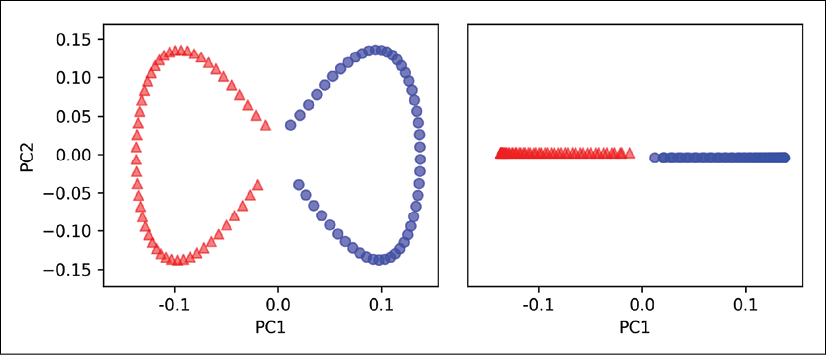
Unfortunately, there is no universal value for the tuning parameter, , that works well for different datasets. Finding a value that is appropriate for a given problem requires experimentation. In Chapter 6, Learning Best Practices for Model Evaluation and Hyperparameter Tuning, we will discuss techniques that can help us to automate the task of optimizing such tuning parameters. Here, we will use values for that have been found to produce good results.

Example 2 – separating concentric circles

In the previous subsection, we saw how to separate half-moon shapes via KPCA. Since we put so much effort into understanding the concepts of KPCA, let's take a look at another interesting example of a nonlinear problem, concentric circles:

>>> from sklearn.datasets import make_circles
>>> X, y = make_circles(n_samples=1000,
...                     random_state=123, noise=0.1,
...                     factor=0.2)
>>> plt.scatter(X[y == 0, 0], X[y == 0, 1],
...             color='red', marker='^', alpha=0.5)
>>> plt.scatter(X[y == 1, 0], X[y == 1, 1],
...             color='blue', marker='o', alpha=0.5)
>>> plt.tight_layout()
>>> plt.show()

Again, we assume a two-class problem where the triangle shapes represent one class, and the circle shapes represent another class:

Let's start with the standard PCA approach to compare it to the results of the RBF kernel PCA:

>>> scikit_pca = PCA(n_components=2)
>>> X_spca = scikit_pca.fit_transform(X)
>>> fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7,3))
>>> ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1],
...               color='red', marker='^', alpha=0.5)
>>> ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1],
...               color='blue', marker='o', alpha=0.5)
>>> ax[1].scatter(X_spca[y==0, 0], np.zeros((500,1))+0.02,
...               color='red', marker='^', alpha=0.5)
>>> ax[1].scatter(X_spca[y==1, 0], np.zeros((500,1))-0.02,
...               color='blue', marker='o', alpha=0.5)
>>> ax[0].set_xlabel('PC1')
>>> ax[0].set_ylabel('PC2')
>>> ax[1].set_ylim([-1, 1])
>>> ax[1].set_yticks([])
>>> ax[1].set_xlabel('PC1')
>>> plt.tight_layout()
>>> plt.show()

Again, we can see that standard PCA is not able to produce results suitable for training a linear classifier:

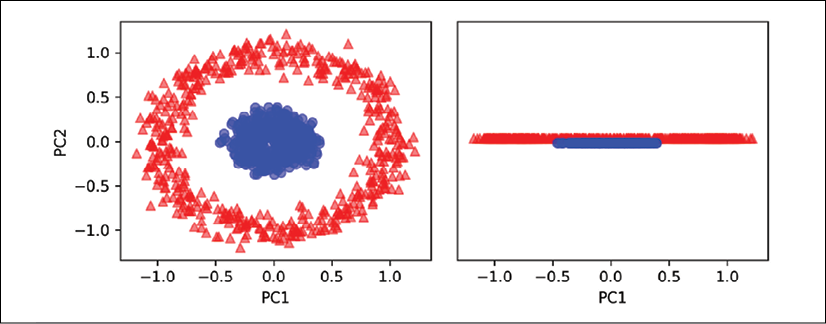
Given an appropriate value for , let's see if we are luckier using the RBF KPCA implementation:

>>> X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
>>> fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))
>>> ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
...               color='red', marker='^', alpha=0.5)
>>> ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
...               color='blue', marker='o', alpha=0.5)
>>> ax[1].scatter(X_kpca[y==0, 0], np.zeros((500,1))+0.02,
...               color='red', marker='^', alpha=0.5)
>>> ax[1].scatter(X_kpca[y==1, 0], np.zeros((500,1))-0.02,
...               color='blue', marker='o', alpha=0.5)
>>> ax[0].set_xlabel('PC1')
>>> ax[0].set_ylabel('PC2')
>>> ax[1].set_ylim([-1, 1])
>>> ax[1].set_yticks([])
>>> ax[1].set_xlabel('PC1')
>>> plt.tight_layout()
>>> plt.show()

Again, the RBF KPCA projected the data onto a new subspace where the two classes become linearly separable:

Projecting new data points

In the two previous example applications of KPCA, the half-moon shapes and the concentric circles, we projected a single dataset onto a new feature. In real applications, however, we may have more than one dataset that we want to transform, for example, training and test data, and typically also new examples we will collect after the model building and evaluation. In this section, you will learn how to project data points that were not part of the training dataset.

As you will remember from the standard PCA approach at the beginning of this chapter, we project data by calculating the dot product between a transformation matrix and the input examples; the columns of the projection matrix are the top k eigenvectors (v) that we obtained from the covariance matrix.

Now, the question is how we can transfer this concept to KPCA. If we think back to the idea behind KPCA, we will remember that we obtained an eigenvector (a) of the centered kernel matrix (not the covariance matrix), which means that those are the examples that are already projected onto the principal component axis, v. Thus, if we want to project a new example, , onto this principal component axis, we will need to compute the following:

Fortunately, we can use the kernel trick so that we don't have to calculate the projection, , explicitly. However, it is worth noting that KPCA, in contrast to standard PCA, is a memory-based method, which means that we have to reuse the original training dataset each time to project new examples.

We have to calculate the pairwise RBF kernel (similarity) between each ith example in the training dataset and the new example, :

Here, the eigenvectors, a, and eigenvalues, , of the kernel matrix, K, satisfy the following condition in the equation:

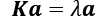
After calculating the similarity between the new examples and the examples in the training dataset, we have to normalize the eigenvector, a, by its eigenvalue. Thus, let's modify the rbf_kernel_pca function that we implemented earlier so that it also returns the eigenvalues of the kernel matrix:

from scipy.spatial.distance import pdist, squareform
from scipy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
    """
    RBF kernel PCA implementation.
    
    Parameters
    ------------
    X: {NumPy ndarray}, shape = [n_examples, n_features]
    
    gamma: float
        Tuning parameter of the RBF kernel
    
    n_components: int
        Number of principal components to return
    
    Returns
    ------------
    alphas {NumPy ndarray}, shape = [n_examples, k_features]
        Projected dataset
    
    lambdas: list
        Eigenvalues
    
    """
    # Calculate pairwise squared Euclidean distances
    # in the MxN dimensional dataset.
    sq_dists = pdist(X, 'sqeuclidean')
    
    # Convert pairwise distances into a square matrix.
    mat_sq_dists = squareform(sq_dists)
    
    # Compute the symmetric kernel matrix.
    K = exp(-gamma * mat_sq_dists)
    
    # Center the kernel matrix.
    N = K.shape[0]
    one_n = np.ones((N,N)) / N
    K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
    
    # Obtaining eigenpairs from the centered kernel matrix
    # scipy.linalg.eigh returns them in ascending order
    eigvals, eigvecs = eigh(K)
    eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
    
    # Collect the top k eigenvectors (projected examples)
    alphas = np.column_stack([eigvecs[:, i]
                             for i in range(n_components)])
    
    # Collect the corresponding eigenvalues
    lambdas = [eigvals[i] for i in range(n_components)]
    return alphas, lambdas

Now, let's create a new half-moon dataset and project it onto a one-dimensional subspace using the updated RBF KPCA implementation:

>>> X, y = make_moons(n_samples=100, random_state=123)
>>> alphas, lambdas = rbf_kernel_pca(X, gamma=15, n_components=1)

To make sure that we implemented the code for projecting new examples, let's assume that the 26th point from the half-moon dataset is a new data point, , and our task is to project it onto this new subspace:

>>> x_new = X[25]
>>> x_new
array([ 1.8713187 ,  0.00928245])
>>> x_proj = alphas[25] # original projection
>>> x_proj
array([ 0.07877284])
>>> def project_x(x_new, X, gamma, alphas, lambdas):
...     pair_dist = np.array([np.sum(
...                 (x_new-row)**2) for row in X])
...     k = np.exp(-gamma * pair_dist)
...     return k.dot(alphas / lambdas)

By executing the following code, we are able to reproduce the original projection. Using the project_x function, we will be able to project any new data example as well. The code is as follows:

>>> x_reproj = project_x(x_new, X,
...            gamma=15, alphas=alphas,
...            lambdas=lambdas)
>>> x_reproj
array([ 0.07877284])

Lastly, let's visualize the projection on the first principal component:

>>> plt.scatter(alphas[y==0, 0], np.zeros((50)),
...             color='red', marker='^',alpha=0.5)
>>> plt.scatter(alphas[y==1, 0], np.zeros((50)),
...             color='blue', marker='o', alpha=0.5)
>>> plt.scatter(x_proj, 0, color='black',
...             label='Original projection of point X[25]',
...             marker='^', s=100)
>>> plt.scatter(x_reproj, 0, color='green',
...             label='Remapped point X[25]',
...             marker='x', s=500)
>>> plt.yticks([], [])
>>> plt.legend(scatterpoints=1)
>>> plt.tight_layout()
>>> plt.show()

As we can now also see in the following scatterplot, we mapped the example, , onto the first principal component correctly:

Kernel principal component analysis in scikit-learn

For our convenience, scikit-learn implements a KPCA class in the sklearn.decomposition submodule. The usage is similar to the standard PCA class, and we can specify the kernel via the kernel parameter:

>>> from sklearn.decomposition import KernelPCA
>>> X, y = make_moons(n_samples=100, random_state=123)
>>> scikit_kpca = KernelPCA(n_components=2,
...               kernel='rbf', gamma=15)
>>> X_skernpca = scikit_kpca.fit_transform(X)

To check that we get results that are consistent with our own KPCA implementation, let's plot the transformed half-moon shape data onto the first two principal components:

>>> plt.scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1],
...             color='red', marker='^', alpha=0.5)
>>> plt.scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1],
...             color='blue', marker='o', alpha=0.5)
>>> plt.xlabel('PC1')
>>> plt.ylabel('PC2')
>>> plt.tight_layout()
>>> plt.show()

As we can see, the results of scikit-learn's KernelPCA are consistent with our own implementation:

Summary

In this chapter, you learned about three different, fundamental dimensionality reduction techniques for feature extraction: standard PCA, LDA, and KPCA. Using PCA, we projected data onto a lower-dimensional subspace to maximize the variance along the orthogonal feature axes, while ignoring the class labels. LDA, in contrast to PCA, is a technique for supervised dimensionality reduction, which means that it considers class information in the training dataset to attempt to maximize the class-separability in a linear feature space.

Lastly, you learned about a nonlinear feature extractor, KPCA. Using the kernel trick and a temporary projection into a higher-dimensional feature space, you were ultimately able to compress datasets consisting of nonlinear features onto a lower-dimensional subspace where the classes became linearly separable.

Equipped with these essential preprocessing techniques, you are now well prepared to learn about the best practices for efficiently incorporating different preprocessing techniques and evaluating the performance of different models in the next chapter.