1.4 Problem-Solving Strategies
Problem solving happens on three different levels:
▶ Strategy: A high-level idea for finding a solution.
▶ Tactics: Methods or patterns that work in many different settings.
▶ Tools: Tricks and techniques that are used in specific situations.
As you progress through this text, you will encounter several different problem-solving strategies. In addition, you will see that computer science uses many different problem-solving tactics. In particular, you will learn to recognize patterns in the problems you solve that lead to patterns in the programs you write. Finally, as you use the Python programming language, you will learn about the tools that Python provides to help you write your solution as a program.
A simple example will illustrate some of what we are talking about. Consider this question: “A class has 12 students. At the beginning of class, each student shakes hands with each of the other students. How many handshakes take place?”
Your first instinct might be to simply say that since each person must shake hands with 11 other people, the answer is 12 × 11 = 132 handshakes. But you would be wrong. To help you make progress toward the correct answer, you can employ a strategy called simplification. Simplification is a strategy that reduces a problem to a trivial size.
Let’s assume that instead of 12 people, only one person is in the classroom. With only a single person, no handshakes will take place. But what happens when a second person enters the classroom? Upon entering the room, the second person must shake hands with the first (and only other) person in the room for one handshake. Now suppose a third person enters the classroom. The third person must shake hands with the first two, making a total of 2 + 1 + 0 = 3 handshakes. The fourth person who enters the room must shake hands with the three people already in the room, so our total handshake count is now 3 + 2 + 1 + 0 = 6. By this time, you should see a pattern of generalization—a technique that enables you to go from some specific examples to a solution that can be implemented as a program.
In our handshaking problem, the pattern tells us that the Nth person to enter the classroom shakes hands with N − 1 other people, and the total number of handshakes is the sum 1 + 2 + 3 + . . . N − 1. At this point, we might simply write a computer program that adds up the numbers from 1 to N − 1. Adding numbers is something that computers are particularly good at. But we will also point out that a general mathematical solution exists for this problem of adding a sequence of numbers:
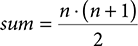
For our handshake problem, we need to add up the numbers from 1 to 1 less than the number of students because as we discovered earlier, with one student, there are no handshakes. Given that there are 12 students, n = 11. Plugging 11 into the formula gives us:
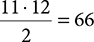
You can verify this result yourself by simply adding the numbers from 1 to 11.
In fact, we can prove that the formula gives us the correct answer by using representation, another important strategy that will solve our problem. Proving that
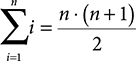
is true for all values of n using mathematical induction would be a daunting task for most people. However, let’s visualize the problem of adding up the numbers from 1 to N as shown in FIGURE 1.1.
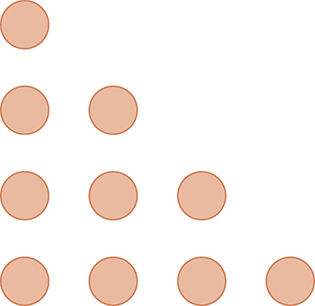
FIGURE 1.1 Representing the sum of the numbers from 1 to N graphically.
In this representation of this slightly simplified problem, we show each of the numbers we want to add as a row of circles, thus representing the addition of 1 + 2 + 3 + 4. Now we could just count the circles to get our answer, but that exercise is not very interesting and does not prove anything. The interesting part comes in FIGURE 1.2, where we have taken all four rows of dots, duplicated them, and flipped them diagonally. The dots now form a rectangle that is 4 rows high and 5 columns wide. It is now easy to see that the total number of dots is just 4 × 5 = 20. But we have twice as many dots as we started with, so the number of dots we started with is 20 ÷ 2 = 10.
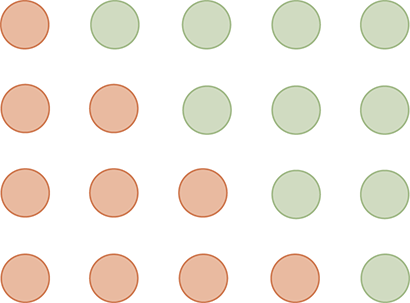
FIGURE 1.2 The sum of the numbers 1 to N is 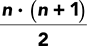 .
.
If you generalize our example a little bit, it is easy to see that this graphical trick works no matter how many rows of dots we use. Therefore, we have shown a proof for an interesting mathematical sequence, but because we chose a good representation for the problem we have not had to do anything more complicated than simple multiplication and division.
