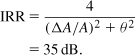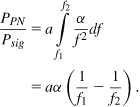Chapter 13. Transceiver Design Example
Having studied the principles of RF architecture and circuit design in the previous chapters, we are now prepared to embark upon the design of a complete transceiver. In this chapter, we design in 65-nm CMOS technology a dual-band transceiver for IEEE 802.11a/g applications. We first translate the standard’s specifications to circuit design parameters and subsequently decide on the architecture and the frequency planning necessary to accommodate the 2.4-GHz and 5-GHz bands. The chapter outline is shown below.

In the circuit designs described in this chapter, the channel length of the transistors is equal to 60 nm unless otherwise stated. The reader is encouraged to review the 11a/g specifications described in Chapter 3.
13.1 System-Level Considerations
In deriving the transceiver specifications, we must bear two points in mind. (1) Since each nonideality degrades the performance to some extent, the budget allocated for each must leave sufficient margin for others. For example, if the RX noise figure is chosen to yield exactly the required sensitivity, then the I/Q mismatch may further degrade the BER. Thus, the overall performance must eventually be evaluated with all of the nonidealities present. (2) Both the TX and the RX corrupt the signal, dictating that each be designed with sufficient margin for the other’s imperfections.
13.1.1 Receiver
For the receiver design, we must determine the required noise figure, linearity, and automatic gain control (AGC) range. In addition, we must decide on the maximum I and Q mismatch that can be tolerated in the downconverted signal.
Noise Figure
As mentioned in Chapter 3, 11a/g specifies a packet error rate of 10%. This translates to a bit error rate of 10−5, which in turn necessitates an SNR of 18.3 dB for 64QAM modulation [1]. Since TX baseband pulse shaping reduces the channel bandwidth to 16.6 MHz, we return to
![]()
and obtain
![]()
for a sensitivity of −65 dBm (at 52 Mb/s). In practice, signal detection in the digital baseband processor suffers from nonidealities, incurring a “loss” of a few decibels. Moreover, the front-end antenna switch exhibits a loss of around 1 dB. For these reasons, and to deliver competitive products, manufacturers typically target an RX noise figure of about 10 dB. Since the 11a/g sensitivities are chosen to require about the same NF for different data rates, the NF of 10 dB must be satisfied for the highest sensitivity (−82 dBm) as well.
Nonlinearity
For RX nonlinearity, we begin with the 1-dB compression point. As computed in Chapter 3, for 52 subchannels, the peak-to-average ratio reaches 9 dB,1 requiring a P1dB of at least −21 dBm so as to handle a maximum input level of −30 dBm. Allowing 2 dB for envelope variation due to baseband pulse shaping, we select a P1dB of −19 dBm for the receiver. This value corresponds to an IIP3 of about −9 dBm. However, the IIP3 may also be dictated by adjacent channel specifications.
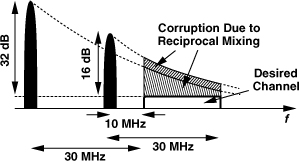
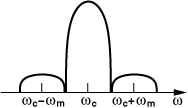
Let us examine the adjacent and alternate channel levels described in Chapter 3. At a sensitivity of −82 dBm, these levels are respectively 16 dB and 32 dB higher, and their intermodulation must negligibly corrupt the desired channel. We represent the desired, adjacent, and alternate channels by A0 cos ω0t, A1 cos ω1t, and A2 cos ω2t, respectively. For a third-order nonlinearity of the form y(t) = α1x(t) + α2x2(t) + α3x3(t), the desired output is given by α1A0 cos ω0t and the IM3 component at ω0 by ![]() (Fig. 13.1). The modulation scheme used with this sensitivity (BPSK) requires an SNR of 4 to 5 dB. Thus, we choose the IM3 corruption to be around −15 dB to allow for other nonidealities:
(Fig. 13.1). The modulation scheme used with this sensitivity (BPSK) requires an SNR of 4 to 5 dB. Thus, we choose the IM3 corruption to be around −15 dB to allow for other nonidealities:
![]()
Figure 13.1 Effect of intermodulation between two blockers.

At this point, we can compute Aj as voltage quantities, substitute their values in the above equation, and determine ![]() . Alternatively, we can maintain the logarithmic quantities and proceed very carefully:
. Alternatively, we can maintain the logarithmic quantities and proceed very carefully:
![]()
Even though the last three terms on the right-hand side are voltage quantities, we replace them with their respective power levels in dBm:2 20 log A1 = −63 dBm, 20 log A2 = −47 dBm, and 20 log A0 = −79 dBm. It follows that
![]()
That is,
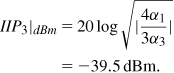
In Problem 13.1, we repeat this calculation for the data rate of 54 Mb/s and sensitivity of −65 dBm, obtaining roughly the same IIP3. Thus, the IIP3 value dictated by adjacent channel specifications is relatively relaxed in 11a/g. Of course, the baseband filters must still sufficiently attenuate the adjacent and alternate channels.
It is important to recognize the different design requirements related to the two IP3 values obtained above. The IP3 corresponding to the 1-dB compression point (sometimes called the “in-channel” IP3) is satisfied if compression by the desired signal is avoided. This can be accomplished by lowering the receiver gain for high input levels. On the other hand, the IP3 arising from adjacent channel specifications (sometimes called the “out-of-channel” IP3) must be satisfied while the desired signal is only 3 dB above the reference sensitivity. In this case, the RX gain cannot be reduced to improve the linearity because the sensitivity degrades.
We now turn our attention to the IP2 of the receiver. In this case, we are concerned with the demodulation of an interferer’s envelope as a result of even-order nonlinearity. Since 64QAM OFDM interferers exhibit about 9 dB of peak-to-average ratio and hence a relatively “deep” amplitude modulation, this effect may appear particularly severe. However, as described in [2], the required IIP2 is around 0 dBm, a value readily obtained in typical designs.
AGC Range
The receiver must automatically control its gain if the received signal level varies considerably. In order to determine the RX gain range, we consider both the 11a/g rate-dependent sensitivities described in Chapter 3 and the compression specification. The input level may vary from −82 dBm (for 6 Mb/s) to −65 dBm (for 54 Mb/s), and in each case the signal is amplified to reach the baseband ADC full scale, e.g., 1 Vpp (equivalent to +4 dBm in a 50-Ω system).3 It follows that the RX gain must vary to accommodate the rate-dependent sensitivities. The challenge is to realize this gain range while maintaining a noise figure of about 10 dB (even at the lowest gain, for 54 Mb/s) and an (out-of-channel) IIP3 of about −40 dBm (even at the highest gain, for 6 Mb/s).
The receiver gain range is also determined by the maximum allowable desired input level (−30 dBm). As explained in the above example, the baseband ADC preferably avoids clipping the peaks of the waveforms. Thus, the RX gain in this case is around 32 dB for BPSK (to raise the level from −30 dBm + 2dB to +4 dBm) signals and 23 dB for 64QAM inputs (to raise the level from −30 dBm + 11 dB to +4 dBm). In other words, the RX gain must vary from (a) 84 dB to 58 dB with no NF degradation and an IIP3 of −42 dBm (above example), and (b) from 58 dB to 23 dB with at most a dB-per-dB rise in the NF and at least a dB-per-dB rise in P1dB.4
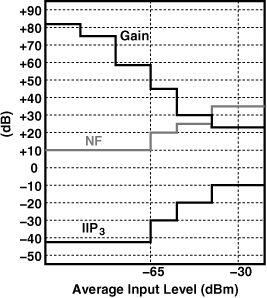
Figure 13.2 sketches the required RX behavior in terms of its gain, NF, and IIP3 variation with the input signal level. The actual number of steps chosen here depends on the design of the RX building blocks and may need to be quite larger than that depicted in Fig. 13.2.
Figure 13.2 Required RX gain switching and NF and IIP3 variations.
I/Q Mismatch
The I/Q mismatch study proceeds as follows. (1) To determine the tolerable mismatch, we must apply in system simulations a 64QAM OFDM signal to a direct-conversion receiver and measure the BER or the EVM. Such simulations are repeated for various combinations of amplitude and phase mismatches, yielding the acceptable performance envelope. (2) Using circuit simulations and random device mismatch data, we must compute the expected I/Q mismatches in the quadrature LO path and the downconversion mixers. (3) Based on the results of the first two steps, we must decide whether the “raw” matching is adequate or calibration is necessary. For 11a/g, the first step suggests that an amplitude mismatch of 0.2 dB and a phase mismatch of 1.5º are necessary [3]. Unfortunately such tight matching requirements are difficult to achieve without calibration.
In light of reported IRR values, the foregoing example suggests that this level of matching is possible without calibration. However, in practice it is difficult to maintain such stringent matching across the entire 11a band with a high yield. Most 11a/g receivers therefore employ I/Q calibration.
13.1.2 Transmitter
The transmitter chain must be linear enough to deliver a 64QAM OFDM signal to the antenna with acceptable distortion. In order to quantify the tolerable nonlinearity, a TX or PA model must be assumed and simulated with such a signal. The quality of the output is then expressed in terms of the bit error rate or the error vector magnitude. For example, the [5] employs the Rapp (static) model [4]:

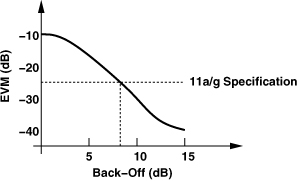
where α denotes the small-signal gain around Vin = 0, and V0 and m are fitting parameters. For typical CMOS PAs, m ≈ 2 [5]. A 64QAM OFDM signal experiencing this nonlinearity yields the EVM shown in Fig. 13.4 as a function of the back-off from P1dB. It is observed that a back-off of about 8 dB is necessary to meet the 11a/g specification, as also mentioned in [3]. Thus, for an output power of 40 mW (= +16 dBm), the TX output P1dB must exceed approximately +24 dBm.5
Figure 13.4 EVM characteritics as a function of back-off.
As explained in Chapter 4, two TX design principles help achieve a high linearity: (1) assign most of the gain to the last PA stage so as to minimize the output swing of the preceding stages, and (2) minimize the number of stages in the TX chain.
The gain of the TX chain from the baseband to the antenna somewhat depends on the design details. For example, a baseband swing of 0.2 Vpp requires a gain of 20 to reach an output swing of 4 Vpp (= +16 dBm).6 As explained in Chapter 4, it is desirable to employ a relatively large baseband swing so as to minimize the effect of dc offsets and hence the carrier feedthrough, but mixer nonlinearity constrains this choice. For now, we assume a differential baseband swing of 0.2 Vpp in each of the I and Q paths.
The I/Q imbalance necessary in the TX is similar to that given for the RX in Section 13.1.1 (0.2 dB and 1.5º), requiring calibration in the transmit path as well. The carrier feedthrough is another source of corruption in direct-conversion transmitters. For 11a/g systems, a feedthrough of about −40 dBc is achieved by means of baseband offset cancellation [5].
13.1.3 Frequency Synthesizer
For the dual-band transceiver developed in this chapter, the synthesizer must cover the 2.4-GHz and 5-GHz bands with a channel spacing of 20 MHz. In addition, the synthesizer must achieve acceptable phase noise and spur levels. We defer the band coverage issues to Section 13.1.4 and focus on the latter two here.
The phase noise in the receive mode creates reciprocal mixing and corrupts the signal constellation. The former effect must be quantified with the adjacent channels present. The following example illustrates the procedure.
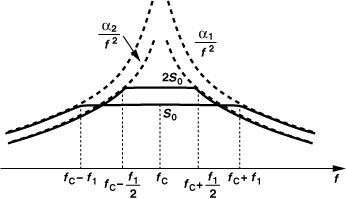
In the absence of reciprocal mixing, the synthesizer phase noise still corrupts the signal constellation. For this effect to be negligible in 11a/g, the total integrated phase noise must remain less than 1º [3]. To compute the integrated phase noise, Pφ, we approximate the synthesizer output spectrum as shown in Fig. 13.6: with a plateau from fc to the edge of the synthesizer loop bandwidth (fc ± f1) and a declining profile given by α/(f − fc)2 beyond fc ± f1. Denoting the value of α/(f − fc)2 at f = fc ± f1 by S0, we have ![]() and
and
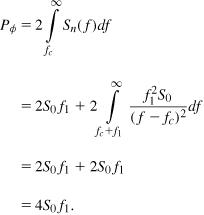
Figure 13.6 Typical phase-locked phase noise profile.
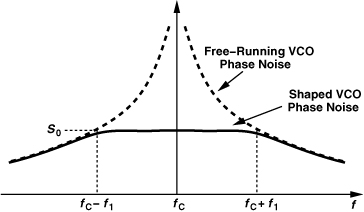
Let us assume that the synthesizer loop bandwidth, f1, is about one-tenth of the channel spacing. For ![]() to be less than 1º = 0.0175 rad, we have S0 = 3.83 × 10−11 rad2/Hz = −104 dBc/Hz. That is, the phase noise of the free-running VCO must be less than −104 dBc/Hz at 2-MHz offset, a more stringent requirement than the phase noise obtained in the above example at 1-MHz offset. The actual phase noise must be 3 dB lower to accommodate the TX VCO corruption as well. We will therefore bear in mind a target free-running phase noise of −104 + 6 − 3 = −101 dBc/Hz at 1-MHz offset.
to be less than 1º = 0.0175 rad, we have S0 = 3.83 × 10−11 rad2/Hz = −104 dBc/Hz. That is, the phase noise of the free-running VCO must be less than −104 dBc/Hz at 2-MHz offset, a more stringent requirement than the phase noise obtained in the above example at 1-MHz offset. The actual phase noise must be 3 dB lower to accommodate the TX VCO corruption as well. We will therefore bear in mind a target free-running phase noise of −104 + 6 − 3 = −101 dBc/Hz at 1-MHz offset.
The synthesizer output spurs must also be considered. For an input level of −82 dBm +3 dB = −79 dBm, spurs in the middle of the adjacent and alternate channels downconvert blockers that are 16 dB and 32 dB higher, respectively. Thus, the spur levels at 20-MHz and 40-MHz offset must be below roughly −36 dBc and −52 dBc, respectively, so that each introduces a corruption of −20 dB. These specifications are relatively relaxed.
The spurs also impact the transmitted signal. To estimate the tolerable spur level, we return to the 1º phase error mentioned above (for random phase noise) and force the same requirement upon the effect of the (FM) spurs. Even though the latter are not random, we expect their effect on the EVM to be similar to that of phase noise. To this end, let us express the TX output in two cases, only with phase noise, φn(t):
![]()
and only with a small FM spur
![]()
For the total rms phase deviation to be less than 1º = 0.0175 rad, we have
![]()
The relative sideband level in xTX2(t) is equal to KVCOam/(2ωm) = 0.0124 = −38 dBc.
13.1.4 Frequency Planning
A direct-conversion transceiver is a natural choice for our 11a/g system. However, it is not obvious how the necessary LO frequencies and phases should be generated. We wish to cover approximately 5.1 GHz to 5.9 GHz for 11a and 2.400 GHz to 2.480 GHz for 11g while providing quadrature outputs and avoiding LO pulling in the TX mode.
Let us consider several different approaches.
• Two separate quadrature VCOs for the two bands, with their outputs multiplexed and applied to the feedback divider chain [Fig. 13.9(a)]. In this case, the four VCO inductors lead to the floor plan shown in Fig. 13.9(b), imposing a large spacing between the 11a and 11g signal paths. This issue becomes critical if the two paths are to share high-frequency circuits (e.g., LNAs and mixers). Also, the 11a VCO must provide a tuning range of about ±15%. Finally, LO pulling proves serious.
• One quadrature VCO serving both bands [Fig. 13.9(c)]. Here, the floor plan is more compact, but the VCO must tune from 4.8 GHz to 5.9 GHz, i.e., by about ±21%. The issue of LO pulling persists for the 11a band and is somewhat serious for the 11g band if the second harmonic of the 11g PA output couples to the VCO. For this reason, it is desirable to implement the 11g PA in fully-differential form [but without symmetric inductors (Chapter 7)].
• One differential VCO operating from 2 × 4.8 GHz to 2 × 5.9 GHz [Fig. 13.9(d)]. This choice allows a compact floor plan but requires (1) a tuning range of ±21%, (2) differential 11a and 11g PAs, and (3) a ÷2 circuit that robustly operates up to 12 GHz, preferably with no inductors. Fortunately, the raw speed of transistors in 65-nm CMOS technology permits such a divider design.
Figure 13.9 (a) Use of two VCOs for 11a and 11g bands, (b) TRX floor plan for (a), (c) use of a VCO and a divider for the two bands, (d) use of a VCO at twice the carrier frequency to avoid injection pulling, and (e) use of two VCOs to relax tuning range requirement.
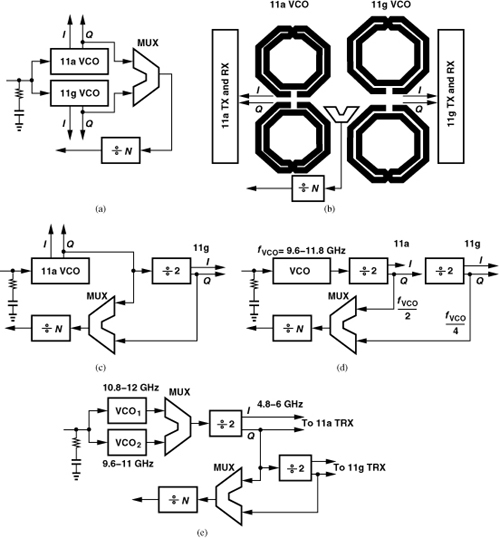
We expect that the relatively high operation frequency and wide tuning range required of the VCO in Fig. 13.9(d) inevitably result in a high phase noise. We therefore employ two VCOs, each with about half the tuning range but with some overlap to avoid a blind zone [Fig. 13.9(e)]. A larger number of VCOs can be utilized to allow an even narrower tuning range for each, but the necessary additional inductors complicate the routing.
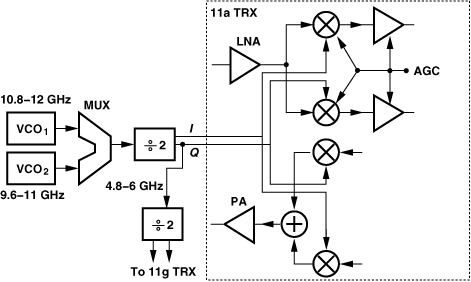
The frequency plan depicted in Fig. 13.9(e) resolves most of the issues that we have encountered, with the proviso that the two PAs are implemented differentially. We must now decide how the synthesizer is shared between the TX and RX paths. Shown in Fig. 13.11 is one scenario where the synthesizer outputs directly drive both paths. In practice, buffers may be necessary before and after the long wires.
Figure 13.11 TRX floor plan with two VCOs running at twice the carrier frequency.
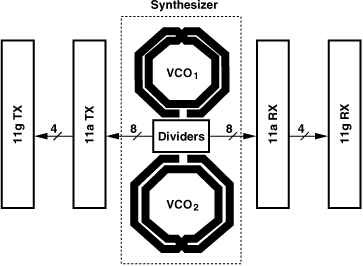
Figure 13.13 shows the overall transceiver architecture developed so far. As seen later, the same RX path can in fact be used for 11a and 11g.
Figure 13.13 Final transceiver architecture.
13.2 Receiver Design
The 11a/g receiver chains are designed for their respective input frequency ranges with the required NF, linearity, gain, and automatic gain control (AGC). The AGC is realized by discrete gain control along the chain and controlled by the digital inputs provided by the baseband processor.
13.2.1 LNA Design
The two 5-GHz design examples described in Chapter 5 are candidates for the 11a receiver. But is it possible to employ only one LNA for the two bands? Let us explore another LNA topology here.
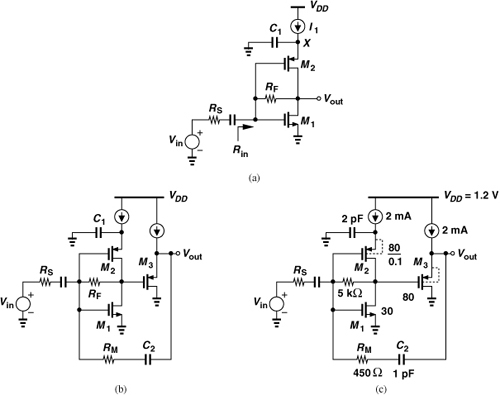
Consider the resistive-feedback LNA shown in Fig. 13.14(a). Here, M2 serves as both a load and an amplifying device, yielding a lower noise figure than if the load is passive. Current source I1 defines the bias of M1 and M2, and C1 creates an ac ground at node X. This circuit can potentially cover the frequency range of 2.4 GHz to 6 GHz. In Problem 13.7, we prove that
![]()
and
![]()
Figure 13.14 (a) LNA with resistive feedback, (b) addition of source follower, (c) complete LNA design.
Equating Rin to RS and making a substitution in the denominator of Eq. (13.27), we have
![]()
We now make two observations based on rough estimates. Suppose (gm1 + gm2) (rO1||rO2) ![]() 1. First, from Eq. (13.28),
1. First, from Eq. (13.28),
![]()
For Rin ≈ 50 Ω, we surmise that the first term should be on the order of 10 to 20 Ω (as it affects the noise figure) and the second, 30 to 40 Ω. That is, RF cannot exceed 300 to 400Ω if (gm1 + gm2)(rO1||rO2) is around 10. Second, from Eq. (13.29), we can compute the gain with gm1 + gm2 ≈ (20Ω)−1, rO1||rO2 ≈ 200Ω,8 and RF = 300Ω, obtaining Vout/Vin = −2.8. In practice, minimum-length devices in 65-nm technology yield a smaller value for (gm1 + gm2)(rO1||rO2) and hence even a lower gain. The circuit thus suffers from a tight trade-off between the input matching and the gain.
In order to achieve a higher gain while providing input matching, we modify the circuit to that shown in Fig. 13.14(b). In this case, RF is large, only establishing proper dc level at the gates of M1 and M2 and allowing a higher voltage gain. The source follower, on the other hand, drives a moderate resistance, RM, to match the input. For a large RF and negligible body effect and channel-length modulation in M3, the input resistance is given by the feedback resistance divided by one plus the loop gain:
![]()
(Why is ![]() included in the numerator?) Lacking the rO1||rO2 term in the numerator of (13.28), this result is more favorable as it permits a larger RM. If Rin = RS and
included in the numerator?) Lacking the rO1||rO2 term in the numerator of (13.28), this result is more favorable as it permits a larger RM. If Rin = RS and ![]() , then the gain is simply equal to 1/2 times the voltage gain of the inverter:
, then the gain is simply equal to 1/2 times the voltage gain of the inverter:
![]()
For example, if (gm1 + gm2)(rO1||rO2) = 10, then a gain of 14 dB is obtained.
Figure 13.14(c) depicts the final LNA design. We should make a few remarks here. First, with a 1.2-V supply, |VGS2| + VGS1 must remain below about 1 V, requiring wide transistors. Second, to increase the gain, the channel length of M2 is raised to 0.1 μm. Third, to minimize |VGS2| and |VGS3|, the n-well of each device is tied to its source.
Figure 13.15 plots the simulated characteristics of the LNA across a frequency range of 2 GHz to 6 GHz. The worst-case |S11|, NF, and gain9 are equal to −16.5 dB, 2.35 dB, and 14.9 dB, respectively. Shown in Fig. 13.16 is the LNA gain as a function of the input level at 6 GHz. By virtue of negative feedback, the LNA achieves a P1dB of about −14 dBm.10
Figure 13.15 Simulated characteristics of 11a/g LNA.
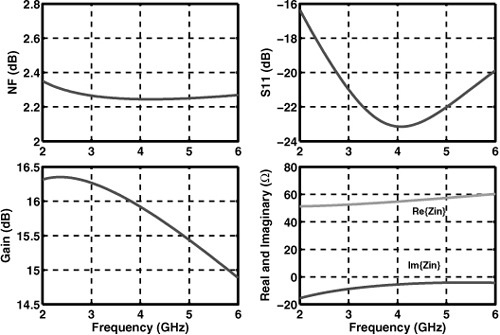
Figure 13.16 LNA compression characteristic.

13.2.2 Mixer Design
The choice between passive and active mixers depends on several factors, including available LO swings, required linearity, and output flicker noise. In this transceiver design, we have some flexibility because (a) 65-nm CMOS technology can provide rail-to-rail LO swings at 6 GHz, allowing passive mixers, and (b) the RX linearity is relatively relaxed, allowing active mixers. Nonetheless, the high flicker noise of 65-nm devices proves problematic in active topologies.
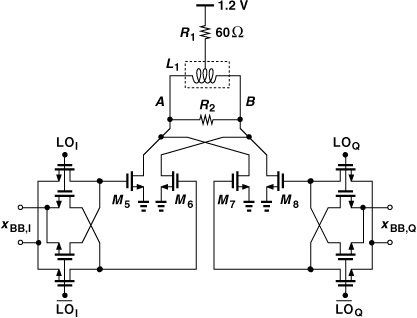
We consider a single-balanced passive mixer followed by a simple baseband amplifier (Fig. 13.17). Here, to minimize the amplifier’s flicker noise, large PMOS devices are employed. The gate bias voltage of the differential pair is defined by Vb and is 0.2 V above ground to ensure M3 and M4 operate in saturation. Note that two instances of this chain are required for quadrature downconversion, drawing a total supply current of 10 mA.
Figure 13.17 Downconversion mixer design.

Using the equations derived for voltage-driven sampling (non-return-to-zero) mixers in Chapter 6, we can compute the characteristics of the above circuit. Transistors M3 and M4 present a load capacitance of CL ≈ (2/3)WLCox ≈ 130 fF to the mixer devices. The differential noise measured between A and B is thus given by
![]()
where R1,2 denotes the on-resistance of M1 and M2 and is about 100 Ω. It follows that ![]() . Assuming a voltage gain of about unity from Vin to VAB, we can determine the noise figure with respect to a 50-Ω source by dividing
. Assuming a voltage gain of about unity from Vin to VAB, we can determine the noise figure with respect to a 50-Ω source by dividing ![]() by the noise of a 50-Ω resistor11 and adding 1 to the result. That is, NF = 11.31 = 10.1 dB at fLO = 6 GHz. Simulations confirm this value and reveal negligible flicker noise at A and B.
by the noise of a 50-Ω resistor11 and adding 1 to the result. That is, NF = 11.31 = 10.1 dB at fLO = 6 GHz. Simulations confirm this value and reveal negligible flicker noise at A and B.
The circuit of Fig. 13.17 entails a number of issues. First, though incorporating large transistors, the differential pair still contributes significant flicker noise, raising the NF by several dB at 100 kHz. The trade-off here lies between the impedance that this chain presents to the LNA and the flicker noise of M3 and M4.
Second, the LNA must drive four switches and their sampling capacitors, thereby sustaining a heavy load. Thus, the LNA gain and input matching may degrade. In other words, the LNA and mixer designs must be optimized as one entity.
Third, the inverse dependence of Vn,AB upon fLO in Eq. (13.33) implies that the mixer suffers from a higher noise figure in the 11g band. This is partially compensated by the higher input impedance of the mixer and hence greater LNA gain.
Figure 13.18 plots the simulated double-sideband noise figure of the mixer of Fig. 13.17 with respect to a 50-Ω source impedance. For a 6-GHz LO, the NF is dominated by the flicker noise of the baseband amplifier at 100-kHz offset. For a 2.4-GHz LO, the thermal noise floor rises by 3 dB. The simulations assume a rail-to-rail sinusoidal LO waveform.
Figure 13.18 Simulated NF of mixer at (a) 2.4 GHz, (b) 6 GHz.

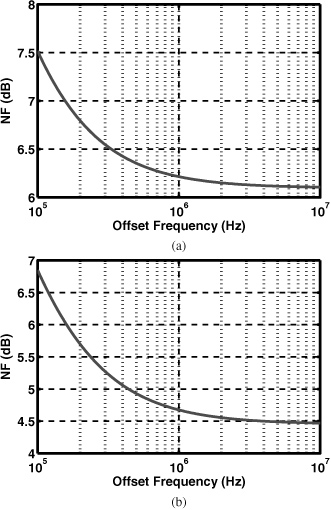
Figure 13.19 shows the overall RX chain, and Fig. 13.20 plots its simulated double-sideband noise figure. The RX noise figure varies from 7.5 dB to 6.1 dB at 2.4 GHz and from 7 dB to 4.5 dB at 6 GHz. These values are well within our target of 10 dB.
Figure 13.19 Overall 11a/g receiver design.

Figure 13.20 Simulated RX NF at (a) 2.4 GHz and (b) 6 GHz.
13.2.3 AGC
As mentioned in Section 13.1.1, the RX gain must be programmable from 23 dB to 58 dB so as to withstand a maximum input level of −30 dBm. The principal challenge in realizing a variable gain in the front end is to avoid altering the RX input impedance. For example, if resistor RM in Fig. 13.14(c) varies, so does the S11. Fortunately, as shown in Fig. 13.16, the LNA 1-dB compression point is well above −30 dBm, allowing a fixed LNA gain for the entire input level range.
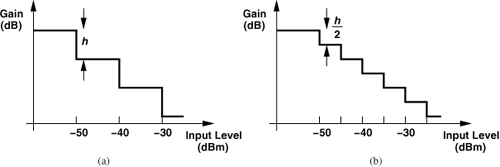
In order to determine where in the receiver chain we must vary the gain, we first plot the overall RX gain characteristic (Figure 13.21), obtaining an input P1dB of −26 dBm. Dominated by the baseband differential pair, the RX P1dB is quite lower than that of the LNA. It is therefore desirable to lower the mixer gain as the average RX input level approaches −30 dBm, especially because the peak-to-average ratio of 11a/g signals can reach 9 dB. As shown in Fig. 13.22, this is accomplished by inserting transistors MG1-MG3 between the differential outputs of the mixer. For an input level of around −50 dBm, MG1 is turned on, reducing the gain by about 5 dB. For an input level of −40 dBm, both MG1 and MG2 are turned on, lowering the gain by 10 dB. Finally, for an input level of −30 dBm, all three transistors are turned on, dropping the gain by 15 dB. Of course, we hope that the RX P1dB rises by approximately the same amount in each case, reaching a comfortable value in the low-gain mode. We call this arrangement the “coarse AGC.”
Figure 13.21 Compression characteristic of 11a/g receiver.

Figure 13.22 Coarse AGC embedded within downconversion mixer.
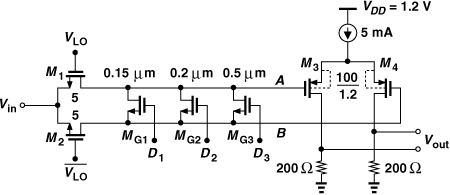
The necessary widths of MG1-MG3 are obtained from simulations to be 0.15 μm, 0.2 μm, and 0.5 μm, respectively (L = 60 nm). Figure 13.23 plots the receiver gain, P1dB, and NF for the different gain settings.
Figure 13.23 Receiver performance as a function of gain setting.
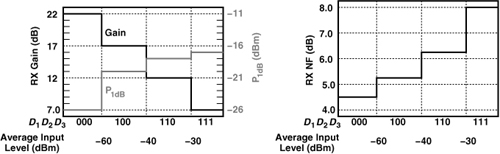
We should make two remarks. First, owing to their small dimensions, MG1-MG3 suffer from large threshold variations. It is therefore preferable to increase both the width and length of each device by a factor of 2 to 5 while maintaining the desired on-resistance. Second, the characteristics of Fig. 13.23 indicate that the RX P1dB hardly exceeds −18 dBm even as the gain is lowered further. This is because, beyond this point, the nonlinearity of the LNA and mixer (rather than the baseband amplifier) dominates.
With a maximum gain of 22 dB provided by the front end, the RX must realize roughly another 40 dB of gain in the baseband (Example 13.2) (the “fine AGC”). In practice, the amplification and channel-selection filtering are interspersed, thus relaxing the linearity of the gain stages.12
In order to minimize the burden on the ADC, the AGC typically employs a gain step of 1 or 2 dB. Of course, in systems with a narrow channel bandwidth, e.g., GSM, the baseband ADC runs at a relatively low speed and can be designed for a wide dynamic range, thereby relaxing the AGC requirements.
Another issue related to AGC is the variation of the baseband DC offset as the gain changes. Since switching the LNA or mixer gain may alter the amount of the LO coupling to the RX input and hence the self-mixing result, the DC offset changes. To deal with this effect, one can (1) perform offset cancellation for each gain setting and store the results in the digital domain so that the offset is corrected as the gain is switched, or (2) increase the ADC dynamic range to accommodate the uncorrected offset.
The baseband gain and filtering stages should negligibly degrade the RX noise and linearity. In practice, however, noise-linearity-power trade-offs make it difficult to fulfill this wish with a reasonable power consumption. Consequently, the linearity of typical receivers (in the high-gain mode) is limited by that of the baseband stages rather than the front end.
We now implement the fine AGC. Figure 13.26(a) depicts a variable-gain amplifier (VGA)13 suited for use in the baseband. Here, the gain is reduced by raising the degeneration resistance: in the high-gain mode, MG1-MGn are on, and to lower the gain, we turn off MG1; or MG1 and MG2; or MG1, MG2, and MG3; etc. Note that as the gain falls, the stage becomes more linear, a desirable and even necessary behavior for VGAs.
Figure 13.26 (a) Simplified and (b) complete VGA circuit diagrams. (The n-wells are connected to VDD.)
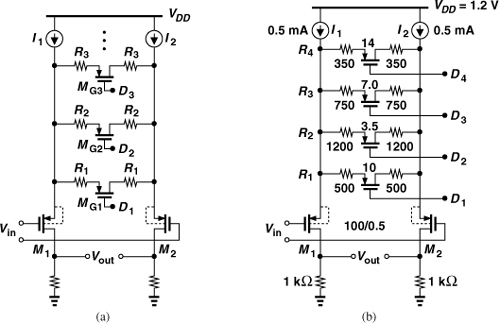
In the circuit of Fig. 13.26(a), the nonlinearity of MG1-MGn may manifest itself for large input swings. For this reason, these transistors must be wide enough that their on-resistance is only a fraction (e.g., one-tenth to one-fifth) of 2Rj. The value of each Rj is chosen so as to provide a linear-in-dB gain characteristic.
Figure 13.26(b) shows the design in detail. For M1 and M2, we employ a long channel, reducing the nonlinearity due to their voltage-dependent output resistance, and tie their source and n-well, allowing a headroom of about 200 mV for I1 and I2 and minimizing their noise contribution (Problem 13.8). The degeneration branches provide a gain step of 2 dB.
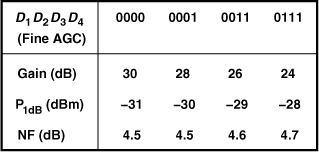
Table 13.1 summarizes the simulated RX performance with the VGA placed after the chain. As with the topology of Fig. 13.22, the switches are driven by a “thermometer” code, i.e., D1D2D3D4 “fills” up by one more logical ONE for each 2-dB gain increase. We observe that (a) the RX P1dB drops from −26 dBm to −31 dBm when the VGA is added to the chain, and (b) the noise figure rises by 0.2 dB in the low-gain mode. The VGA design thus favors the NF at the cost of P1dB—while providing a maximum gain of 8 dB.
Table 13.1 Summary of receiver performance with gain switching.
13.3 TX Design
The design of the TX begins with the power amplifier and proceeds backwards. The need for matching networks makes it extremely difficult to realize a PA operating in both 11g and 11a bands. We therefore assume two different PAs.
13.3.1 PA Design
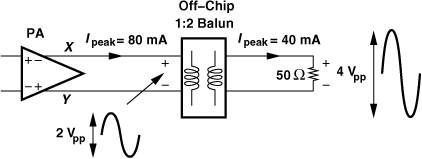
As mentioned in Section 13.1.2, the PA must deliver +16 dBm (40 mW) with an output P1dB of +24 dBm. The corresponding peak-to-peak voltage swings across a 50-Ω antenna are 4 V and 10 V, respectively. We assume an off-chip 1-to-2 balun and design a differential PA that provides a peak-to-peak swing of 2 V, albeit to a load resistance of 50 Ω/22 = 12.5 Ω.14 Figure 13.27 summarizes our thoughts, indicating that the peak voltage swing at X (or Y) need be only 0.5 V.
Figure 13.27 Voltage swings provided by PA.
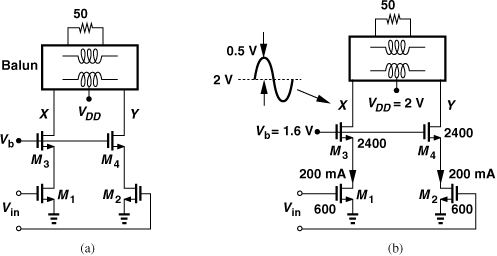
Let us begin with a quasi-differential cascode stage [Fig. 13.28(a)]. As explained in Chapter 12, the choice of Vb is governed by a trade-off between linearity and device stress. If Vb is too high, then the downward voltage swing at X and Y drives M3 and M4 into the triode region, causing the drain voltages of M1 and M2 to change and possibly create compression. If Vb is too low, then the upward voltage swing at X and Y produces an excessive drain-source voltage for M3 and M4.
Figure 13.28 (a) Simplified and (b) complete PA circuit diagrams.
Another key principle in the design of the above stage is that the circuit must reach compression first at the output rather than at the input. To understand this point, suppose, for a given input swing, M1 and M2 experience compression in their ID-VGS characteristic while the output has not reached compression. (Recall that as the gate voltage of either transistor rises, its drain voltage falls, possibly driving the device into the triode region even if M3 and M4 are saturated.) This means that the supply voltage can be lowered without degrading the P1dB. That is, if the input compresses first, then some of the voltage headroom chosen for the output is “wasted.”
Another important principle is that the gain of the above stage must be maximized. This is because a higher gain translates to a lower input swing (for a given output P1dB), ensuring that the circuit does not compress at the input first.
We also recognize that the single-ended load resistance seen at X (or Y) is equal to 50 Ω/22/2 = 6.25 Ω. The circuit must therefore employ wide transistors and high bias currents to drive this load with a reasonable gain.
Figure 13.28(b) shows the resulting design for a gain of 12 dB.15 Fig. 13.29 plots the internal node voltage waveforms of the PA, and Fig. 13.30 depicts the compression characteristic and the (drain) efficiency as a function of the single-ended input level.
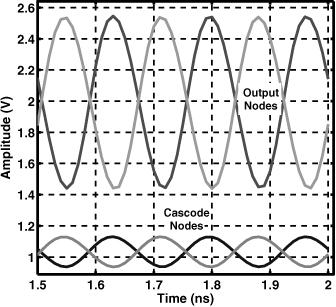
Figure 13.30 PA’s (a) compression characteristic and (b) efficiency.
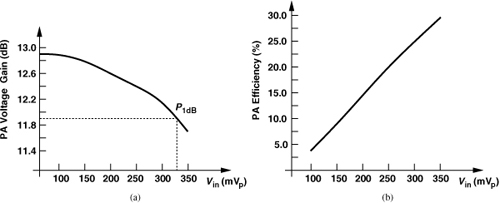
The design meets two criteria: (1) the gain falls by no more than 1 dB when the voltage swing at X (or Y) reaches 2.5 Vpp, (2) the transistors are not stressed for the average output swing, 1 Vpp at X (or Y). The cascode transistors are 2400 μm wide, reducing the voltage swing at the drains of M1 and M2. The input peak-to-peak voltage swing applied at the gate of M1 (and M2) is equal to 0.68 V when the output reaches P1dB.
The above PA stage draws a total current of 400 mA from a 2-V supply, yielding an efficiency of about 30% at the output P1dB and 5% at the average output level of 40 mW. This is the price paid for a back-off of 8 dB. More advanced designs achieve higher efficiencies [7, 8].
Predriver
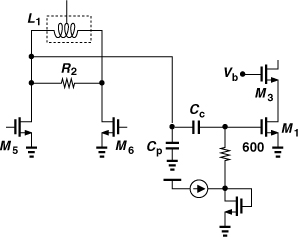
We now turn our attention to the PA predriver stage. The input capacitance of the PA is about 650 fF, requiring a driving inductance of about 1 nH for resonance at 6 GHz. With a Q of 8, such an inductor exhibits a parallel resistance of 300 Ω. The predriver must therefore have a bias current of at least 2.3 mA so as to generate a peak-to-peak voltage swing of 0.68 V. However, for the predriver not to degrade the TX linearity, its bias current must be quite higher.
Figure 13.31 shows the predriver and its interface with the PA. The width and bias current of M5 and M6 are chosen so as to provide a high linearity and a voltage gain of about 7 dB. The load inductor is reduced to 2 × 0.6 nH to accommodate the predriver parasitics. Resistor R1 sustains a voltage drop of 0.5 V, biasing M1 and M2 at their nominal current. In practice, this resistor may be replaced with a tracking circuit to define this current more accurately.
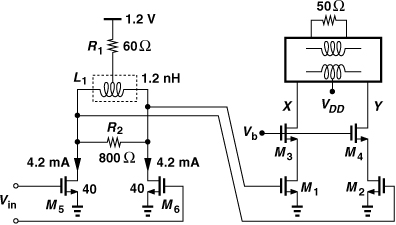
Designed for resonance at 6 GHz with a Q of 8, the predriver suffers from a low gain at 5 GHz. Resistor R2 is added to increase the bandwidth, but a few capacitors must be switched into the tank so as to lower the resonance frequency (Chapter 5). Inductor L1 can also be raised so as to reduce the resonance frequency to about 5.5 GHz.
Common-Mode Stability
Quasi-differential PAs exhibit a higher common-mode gain than differential gain, possibly suffering from CM instability. To understand this point, let us first consider the simple stage shown in Fig. 13.33(a), where a quasi-differential pair drives a 50-Ω load. The circuit is generally stable from the standpoint of differential signals because, as evident from the half circuit in Fig. 13.33(b), the 25-Ω resistance seen by each transistor dominates the load, avoiding a negative resistance at the gate (Chapter 5).
Figure 13.33 (a) Stage driving a floating 50-Ω load, (b) half circuit for differential signals, and (c) half circuit for common-mode signals.
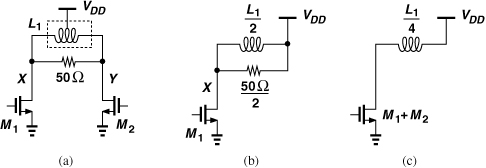
For CM signals, on the other hand, the circuit of Fig. 13.33(a) collapses to that shown in Fig. 13.33(c). The 50-Ω resistor vanishes, leaving behind an inductively-loaded common-source stage, which can exhibit a negative input resistance. To ensure stability, a positive common-mode resistance must drive this stage.
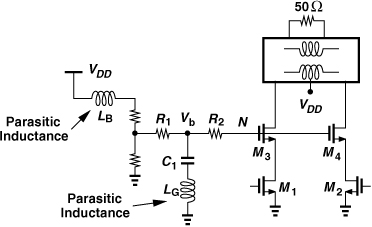
Now consider the circuit of Fig. 13.31 again. For common-mode signals, resistor R1 appears in series with the gate of M1 + M2, improving the stability. Of course, the cascode output stage also helps with the stability, minimizing the negative resistance seen at the gates of M1 and M2—but only if the gates of M3 and M4 are tied to a voltage source with a low impedance. In practice, however, this task proves difficult because of the parasitic inductance in series with VDD or ground. We therefore provide the cascode gate bias through a lossy network as shown in Fig. 13.34. Here, we generate Vb by means of a simple resistive divider, but, to dampen resonances due to LB and LG, we also add R1 and R2. Note that the cascode operation remains intact for differential signals, i.e., node N appears as a virtual ground. This is another advantage of differential realizations.
Figure 13.34 Lossy network used to avoid CM instability.
13.3.2 Upconverter
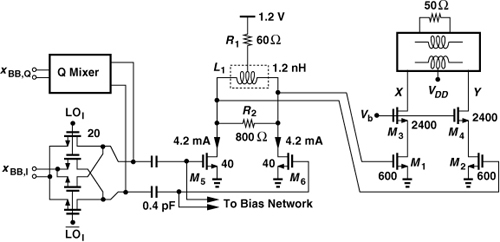
The upconverter must translate the baseband I and Q signals to a 6-GHz center frequency while driving the 40-μm input transistors of the predriver. We employ a passive mixer topology here, assuming that rail-to-rail LO swings are available.
Figure 13.35 shows our first attempt at the upconverter construction and the necessary predriver modification. Each double-balanced mixer output voltage is converted to current, and the results are summed at nodes A and B. This arrangement must deal with two issues. First, since the gate bias voltage of M5-M8 is around 0.6 V, the mixer transistors suffer from a small overdrive voltage if the LO swing reaches only 1.2 V. We must therefore use ac coupling between the mixers and the predriver.
Figure 13.35 Upconverter using passive mixers and V/I converters.
Second, each passive mixer generates a double-sideband output, making it more difficult to achieve the output P1dB required of the TX chain. To understand this point, consider the conceptual diagram in Fig. 13.36(a), where the TX is tested with a single baseband tone (rather than a modulated signal). The gate voltage of M5 thus exhibits a beat behavior with a large swing, possibly driving M5 into the triode region. Note that the drain voltage of M5 has a constant envelope because the upconverted I and Q signals are summed at node A. The key point here is that, to generate a given swing at A, the beating swing at the gate of M5 is larger than a constant-envelope swing that would be used to test only the predriver and the PA [Fig. 13.36(b)]. To overcome this difficulty, we wish to sum the signals before they reach the predriver.
Figure 13.36 (a) Problem of large beat swing at gate of V/I converter transistors, (b) stage without beat component.
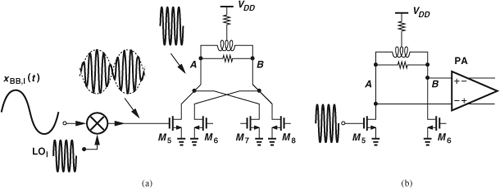
Figure 13.37 shows the final TX design. Here, the mixer outputs are shorted to generate a single-sideband signal and avoid the beat behavior described above. This summation is possible owing to the finite on-resistance of the mixer switches. Simulations indicate that the gain and linearity of this upconverter topology are similar to those of the simple double-balanced counterpart. The baseband dc input of the mixers is around 0.3 V.
In order to determine the TX output P1dB, we can plot the chain’s conversion gain as a function of the baseband swing. The definition of the conversion gain is somewhat arbitrary; we define the gain as the differential voltage swing delivered to the 50-Ω load divided by the differential voltage swing of xBB,I(t) [or xBB,Q(t)].
Figure 13.38 plots the overall TX conversion gain. The TX reaches its output P1dB at VBB,pp = 890 mV, at which point it delivers an output power of +24 dBm. The average output power of +16 dBm is obtained with VBB,pp ≈ 350 mV. The simulations assume a sinusoidal rail-to-rail LO waveform.
Figure 13.38 TX compression characteristic.

The large mixer transistors exhibit a threshold mismatch of 4 to 5 mV, resulting in some carrier feedthrough. A means of offset cancellation may be added to the stages preceding the mixers (usually I and Q low-pass filters) so as to suppress this effect.
13.4 Synthesizer Design
In this section, we design an integer-N synthesizer with a reference frequency of 20 MHz for the 11a and 11g bands. From our analysis in Section 13.1.3, we must target an oscillator phase noise of about −101 dBc/Hz at 1-MHz offset for a carrier frequency of 2.4 GHz or 5 to 6 GHz. Recall from the frequency planning in Section 13.1.4 that the VCOs in fact operate at 10 to 12 GHz and must therefore exhibit a maximum phase noise of −101 + 6 = −95 dBc/Hz at 1-MHz offset.16
13.4.1 VCO Design
We choose the tuning range of the VCOs as follows. One VCO, VCO1, operates from 9.6 GHz to 11 GHz, and the other, VCO2, from 10.8 GHz to 12 GHz. The 200-MHz overlap between the VCOs’ tuning ranges avoids a “blind zone” in the presence of modeling errors and random mismatches between the two circuits. We begin with VCO2.
Let us assume a single-ended load inductance of 0.75 nH (i.e., a differential load inductance of 1.5 nH) with a Q of about 10 in the range of 10 to 12 GHz. Such values yield a single-ended parallel equivalent resistance of 618 Ω, requiring a tail current of about 1.5 mA to yield a single-ended peak-to-peak output swing of (4/π)RpISS = 1.2 V. We choose a width of 10 μm for the cross-coupled transistors to ensure complete switching and assume a tentative load device width of 10 μm to account for the input capacitance of the subsequent frequency divider. Finally, we add enough constant capacitance to each side to obtain an oscillation frequency of about 12 GHz. Figure 13.39(a) shows this preliminary design.
Figure 13.39 (a) Preliminary 12-GHz VCO design, (b) addition of switched capacitors to lower the frequency to 10.8 GHz.

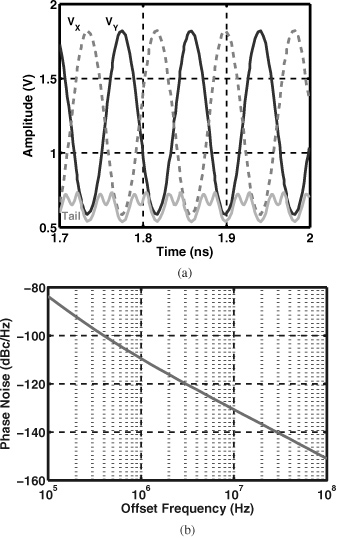
At this point, we wish to briefly simulate the performance of the circuit before adding the tuning devices. Simulations suggest a single-ended peak-to-peak swing of about 1.2 V [Fig. 13.40(a)]. Also, the phase noise at 1-MHz offset is around −109 dBc/Hz [Fig. 13.40(b)], well below the required value. The design is thus far promising. However, as the drain and tail voltage waveforms suggest, the core transistors do enter the deep triode region, making the phase noise sensitive to the tail capacitance (Chapter 8).
Figure 13.40 Simulated (a) waveforms and (b) phase noise of 12-GHz VCO.
Now, we add a switched capacitance of 90 fF to each side so as to discretely tune the frequency from 12 GHz to 10.8 GHz [Fig. 13.39(b)]. As explained in Chapter 8, the size of the switches in series with the 90-fF capacitors must be chosen according to the trade-off between their parasitic capacitance in the off state and their channel resistance in the on state. But a helpful observation in simulations is that the voltage swing decreases considerably if the on-resistance is not sufficiently small. That is, as the switches become wider, the swing is gradually restored.
Figure 13.39(b) depicts the modified design. We simulate the circuit again to ensure acceptable performance. Simulations indicate that the frequency can be tuned from 12.4 GHz to 10.8 GHz, but the single-ended swings fall to about 0.8 V at the lower end. As computed in Chapter 8, this effect arises from the sharp reduction of Rp (the parallel equivalent resistance of the tank) with frequency even if the switched capacitor branch does not degrade the Q. To remedy the situation, we raise the tail current to 2 mA. According to simulations, the phase noise at 1-MHz offset is now equal to −111 dBc/Hz at 10.8 GHz and −109 dBc/Hz at 12.4 GHz. We call S1 a “floating” switch.
In the next step, we add varactors to the VCO and decompose the switched capacitors into smaller units, thus creating a set of discretely-spaced continuous tuning curves with some overlap. Note that the unit capacitors need not be equal. In fact, since at lower frequencies, the effect of a given capacitance change on the frequency is smaller (why?), we may begin with larger units at the lower end. This step of the design demands some iteration in the choice of the varactors’ size and the number and values of the unit capacitors.
After iterations, we arrive at the design in Fig. 13.41(a), where half of the circuit is shown for simplicity. Here, six switched capacitors and a 20-μm varactor provide the necessary tuning range. To reduce the frequency, first Cu6 is switched in, then Cu6+Cu5, etc. We should make two remarks. First, as in Fig. 13.39(b), we still have floating switches even though they are not shown. Ideally, the switch widths are scaled with Cuj, but the minimum width in 65-nm technology is about 0.18 μm and is chosen for the grounded switches. The floating switches have a width of 2 μm for Cu1 and Cu2 and 1.5 μm for Cu3–Cu6.
Figure 13.41 (a) Switched-capacitor array added to VCO for discrete control and (b) coupling capacitor structure.

Second, to obtain a wide continuous tuning range, the gate of the varactor is capacitively coupled to the core and biased at Vb ≈ 0.6 V. As explained in Chapter 8, the “bottom-plate” parasitic of Cc may limit the tuning range. Fortunately, however, our design affords a large constant capacitance on each side, readily absorbing the parasitic of Cc. The coupling capacitor can be realized with parallel plates [Figure 13.41(b)]. The value of Cc is chosen about 10 times the maximum value of the varactor capacitance so as to negligibly reduce the tuning range.
Figure 13.42 shows the VCO’s tuning characteristics obtained from simulations. The control voltage is varied from 0.1 V to 1.1 V, with the assumption that the charge pump preceding the VCO can operate properly across this range. We note that KVCO varies from about 200 MHz/V to 300 MHz/V. Figure 13.43 plots the phase noise with all of the capacitors switched into the tank.
Figure 13.42 VCO tuning characteristics.
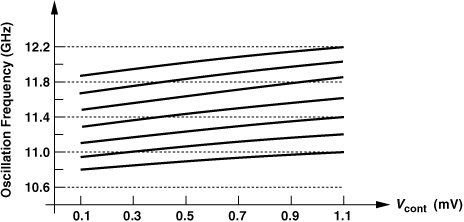
Figure 13.43 VCO phase noise with all capacitors switched into the tank.
In the last step of our VCO design, we replace the ideal tail current source with a current mirror. Shown in Fig. 13.45(a), this arrangement incorporates a channel length of 0.12 μm to improve the matching between the two transistors in the presence of a VDS difference. The width of MSS is chosen so as to create a small overdrive voltage, allowing the VGS to be approximately equal to VDS (≈ 500 mV). This choice makes the transconductance and hence noise current of MSS larger than necessary, but we will thus proceed for now. Note that MREF and IREF are scaled down by only a factor of 2 because the noise of MREF may otherwise dominate.
Figure 13.45 (a) Current mirror used to bias the VCO, (b) modified mirror including a low-pass filter.

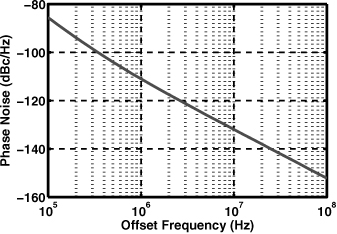
The current mirror drastically raises the phase noise of the VCO, from −111 dBc/Hz to −100 dBc/Hz at 10.8 GHz and from −109 dBc/Hz to −98 dBc/Hz at 12.4 GHz (both at 1-MHz offset) (Fig. 13.46). According to Cadence, most of the phase noise now arises from the thermal and flicker noise of MREF and MSS.
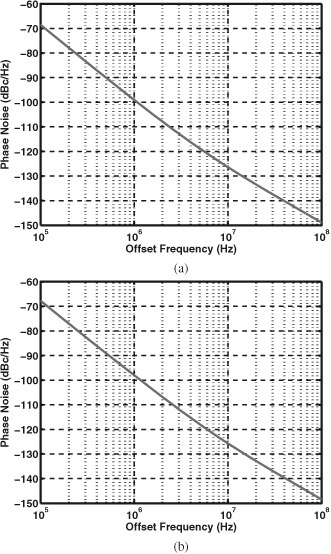
Figure 13.46 VCO phase noise with the current mirror bias at (a) 10.8 GHz and (b) 12 GHz.
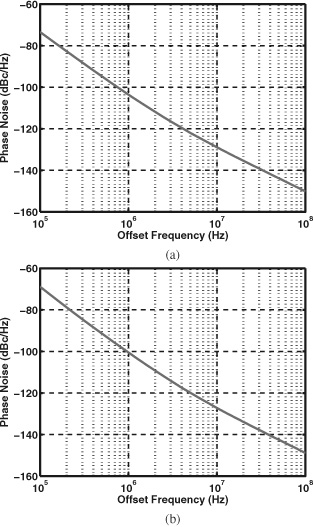
A simple modification can suppress the contribution of MREF. As shown in Fig. 13.45(b), we insert a low-pass filter between the two transistors, suppressing the noise of MREF (and IREF). To obtain a corner frequency well below 1 MHz, we (1) bias MS with a small overdrive voltage, which is provided by the wide diode-connected transistor Mb; (2) select a width of 0.2 μm and a length of 10 μm for MS; and (3) choose a value of 5 pF for Cb. The phase noise at 1-MHz offset is now equal to −104 dBc/Hz at 10.8 GHz and −101 dBc/Hz at 12.4 GHz. Figure 13.47 plots the phase noise of the final design. (The Q of the varactors is assumed to be high.)
Figure 13.47 Phase noise of VCO with low-pass filter inserted in the current mirror at (a) 10.8 GHz and (b) 12 GHz.
Capacitor Cb in Fig. 13.45(b) occupies a relatively large area, even if realized as a MOSFET. One can make MS longer and Cb smaller. Ultimately, however, the drain-source voltage drop of MS due to the gate leakage current of MSS becomes problematic.
While exceeding our phase noise target, the final VCO design still incurs significant noise penalty from the tail transistor, MSS. The reader is encouraged to apply the tail noise suppression techniques described in Chapter 8.
The second VCO must cover a frequency range of 9.6 GHz to 11 GHz. This is readily accomplished by increasing the load inductor from 1.5 nH to 1.8 nH. The remainder of the design need not be modified.
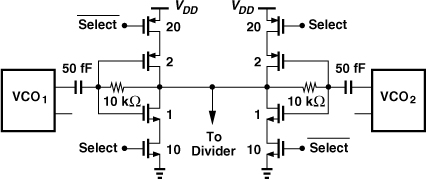
The outputs of the two VCOs must be multiplexed. With rail-to-rail swings available, simple inverters can serve this purpose. As depicted in Fig. 13.49, each inverter is sized according to an estimated fanout necessary to drive the subsequent divide-by-2 circuit. The large transistors controlled by Select and ![]() enable one inverter and disable the other. Also, the feedback resistors bias the enabled inverter in its high-gain region. Note that the VCO outputs have a CM level equal to VDD and are therefore capacitively coupled to the MUX.
enable one inverter and disable the other. Also, the feedback resistors bias the enabled inverter in its high-gain region. Note that the VCO outputs have a CM level equal to VDD and are therefore capacitively coupled to the MUX.
Figure 13.49 Multiplexer selecting output of either VCO.
13.4.2 Divider Design
Divide-by-2 Circuit
The multiplexed VCO outputs must be divided by two so as to generate quadrature outputs. With rail-to-rail swings available at the MUX output, we seek a simple and efficient topology. The favorable speed-power trade-off of the Chang-Park-Kim divider described in Chapter 9 [9] makes it an attractive choice, but this topology does not produce quadrature (or even differential) phases.
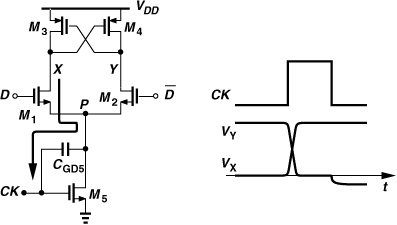
Let us consider a complementary logic style that operates with rail-to-rail swings. Shown in Fig. 13.50(a) is a D latch based on this style. When CK is low, M5 is off and the PMOS devices hold the logical state, when CK goes high, M1 and M2 force the input logical levels upon ![]() and Q.
and Q.
Figure 13.50 (a) Latch topology, and (b) operation when one input goes high.

The above circuit merits two remarks. First, this topology employs dynamic logic; as investigated in Problem 13.10, leakage currents eventually destroy the stored state if CK is low for a long time. Second, the latch is based on ratioed logic, requiring careful sizing. For example, if ![]() is high and CK goes high while D = 1, then, as shown in Fig. 13.50(b), M1 and M5 appear in series and must “overcome” M3. In other words, Ron1 + Ron5 must be small enough to lower VX to slightly below VDD − |VTHP| so that M3 and M4 can begin regeneration. In a typical design, W5 ≈ W1,2 ≈ 2W3,4. Speed requirements may encourage a wider M5.
is high and CK goes high while D = 1, then, as shown in Fig. 13.50(b), M1 and M5 appear in series and must “overcome” M3. In other words, Ron1 + Ron5 must be small enough to lower VX to slightly below VDD − |VTHP| so that M3 and M4 can begin regeneration. In a typical design, W5 ≈ W1,2 ≈ 2W3,4. Speed requirements may encourage a wider M5.
As with other latches, the above circuit may fail if loaded by a large load capacitance. For this reason, we immediately follow each latch in the divide-by-2 circuit by inverters. Figure 13.52 shows the result. The device widths are chosen for the worst case, namely, when the divider drives the TX passive mixers. The inverters present a small load to the latch but must drive a large capacitance themselves, thereby producing slow edges. However, the performance of the TX mixers is no worse than that predicted in Section 13.1.2, where the simulations assume a sinusoidal LO waveform.
Figure 13.52 Divide-by-two stage and its circuit details.

Frequency dividers typically demand a conservative design, i.e., one operating well above the maximum frequency of interest. This is for two reasons: (1) the layout parasitics tend to lower the speed considerably, and (2) in the presence of process and temperature variations, the divider must handle the maximum frequency arriving from the VCO so as to ensure that the PLL operates correctly.
Simulations indicate that the above divide-by-2 circuit and the four inverters draw a total average current of 2.5 mA from a 1.2-V supply at a clock frequency of 13 GHz.
Dual-Modulus Divider
The pulse-swallow counter necessary for the synthesizer requires a prescaler, which itself employs a dual-modulus divider. Such a divider must operate up to about 6.5 GHz.
For this divider, we begin with the ÷3 circuit shown in Fig. 13.53(a) and seek an implementation utilizing the Chang-Park-Kim flipflop. Since this FF provides only a ![]() output, we modify the circuit to that in Fig. 13.53(b), where FF1 is preceded by an inverter.
output, we modify the circuit to that in Fig. 13.53(b), where FF1 is preceded by an inverter.
Figure 13.53 (a) Dual-modulus divider with an explicit AND gate, (b) circuit of (a) with AND gate embedded within second flipflop, and (c) transistor-level implementation of AND and flipflop.
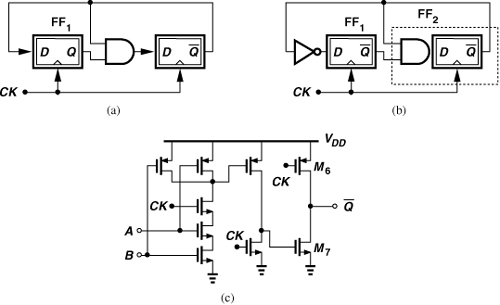
We also wish to merge the AND gate with the second flipflop so as to improve the speed. Figure 13.53(c) depicts this AND/FF combination.
We must now add an OR gate to the topology of Fig. 13.53(a) to obtain a ÷3/4 circuit (Chapter 9). Again, we prefer to merge this gate with either of the flipflops. Figure 13.54 shows the overall ÷3/4 circuit design. The modulus control OR gate is embedded within the AND structure.
Figure 13.54 Transistor-level implementation of dual-modulus prescaler.

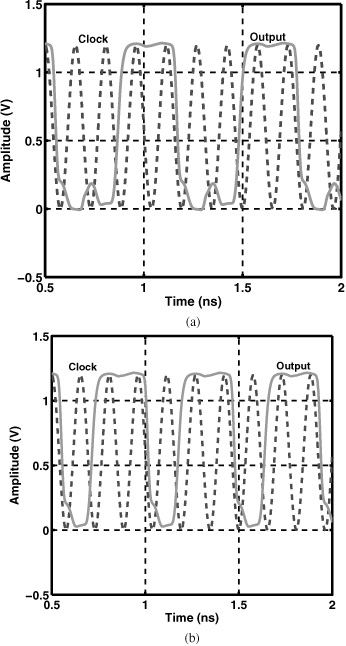
Plotted in Fig. 13.55 are the simulated output waveforms of the circuit in ÷4 and ÷3 modes at a clock frequency of 6.5 GHz. The divider draws 0.5 mA from a 1.2-V supply.
Figure 13.55 Divider input and output waveforms for (a) divide-by-4 and (b) divide-by-3 operation.
The ÷3/4 circuit can now be incorporated in a prescaler as described in Chapter 9. The reader is cautioned that the clock edge on which the asynchronous divide-by-2 stages change their outputs must be chosen carefully to avoid race conditions.
In order to cover a frequency range of 5180 to 5320 MHz in 20-MHz steps, the pulse-swallow counter must provide a divide ratio of NP + S = 259 to 266. If S varies from 9 to 16, then NP = 250 = 53 × 2 and hence N = 10 and P = 25, requiring that the prescaler be designed as a ÷10/11 circuit. Alternatively, one can choose N = 5, P = 50, and a ÷5/6 prescaler.
The high 11a carrier frequencies, namely, from 5745 to 5805 MHz prove troublesome because they are not integer multiples of 20 MHz. An integer-N synthesizer must therefore operate with a reference frequency of 5 MHz, incurring a fourfold reduction in loop bandwidth. Our conservative VCO design in Section 13.4.1 still satisfies the free-running phase noise required of such a loop. The pulse-swallow counter must now provide NP + S = 1149 to 1161. For example, we can choose S = 9–21, N = 10, and P = 114, so that the above prescaler is utilized here as well. A fractional-N loop would be preferable here for accommodating the high band and other crystal frequencies with which the system may need to operate.17 These designs are left as an exercise for the reader.
13.4.3 Loop Design
Let us now design the PFD/CP/LPF cascade and complete the synthesizer loop. The PFD is readily implemented using the NOR-based resettable latch topology described in Chapter 9. The CP and LPF are designed based on the lowest value of KVCO [≈ 2π(200 MHz/V)] and the highest value of the divide ratio, M (=2 × 1161 for a 5-MHz reference).
We begin with a loop bandwidth of 500 kHz and a charge pump current of 1 mA. Thus, 2.5ωn = 2π(500 kHz) and hence ωn = 2π(200 kHz). We have

obtaining C1 = 54.5 pF. Such a capacitor occupies a large chip area. We instead choose Ip = 2 mA and C1 = 27 pF, trading area for power consumption. Setting the damping factor to unity,
![]()
yields R1 = 29.3kΩ. The second capacitor, C2, is chosen equal to 5.4 pF.
For the charge pump, we return to the gate-switched topology described in Chapter 9 as it affords the maximum voltage headroom. Shown in Fig. 13.56, the design incorporates a channel length of 0.12 μm in the output transistors to lower channel-length modulation and wide devices tied to their gates to perform fast switching. To drive these devices, the PFD must be followed by large inverters.
Figure 13.56 Charge pump design.
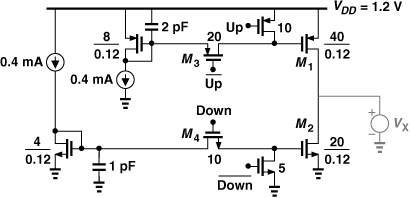
The gate-switched topology still proves rather slow, primarily because of the small overdrive of M3 and M4 in Fig. 13.56. That is, if the up and down pulses are narrow (so as to reduce the effect of mismatch between the up and down currents), then the gate voltages of M1 and M2 do not reach their final values, yielding output currents less than the target.
Figure 13.57 plots the simulated I/V characteristic of the charge pump. As explained in Chapter 9, in this test the Up and Down inputs are both asserted and a voltage source tied between the output node and ground is varied from Vmin (=0.1 V) to Vmax (1.1 V). Ideally equal to zero, the maximum current flowing through this voltage source reveals the deterministic mismatch between the Up and Down currents and the ripple resulting therefrom. In this design, the maximum mismatch occurs at Vout = 1.1 V and is equal to 60 μA, about 3%. If this mismatch creates an unacceptably large ripple, the CP techniques described in Chapters 9 and 10 can be employed.
Figure 13.57 Charge pump I/V characteristic.
Loop Simulation
The simulation of the synthesizer presents interesting challenges. With an input frequency of 5 MHz, the loop takes roughly 20 μs (100 input cycles) to lock. Moreover, for an output frequency of 12 GHz, the transient time step is chosen around 20 ps, requiring about one million time steps. Additionally, even without the discrete tuning logic of Fig. 13.48, the loop contains hundreds of transistors. Each simulation therefore takes several hours!
We begin the simulation by “time contraction” [6]. That is, we wish to scale down the lock time of the loop by a large factor, e.g., K = 100. To this end, we raise fREF by a factor of K and reduce C1, C2, and M by a factor of K (Fig. 13.58). Of course, the PFD and charge pump must operate properly with a reference frequency of 500 MHz. Note that time contraction does not scale R1, Ip, or KVCO, and it retains the value of ζ while scaling down the loop “time constant,” (ζ ωn)−1 = 4πM/(R1IpKVCO), by a factor of K.
Figure 13.58 Scaling loop parameters for time-contracted simulation.

In addition to time contraction, we also employ a behavioral model for the VCO with the same value of KVCO and fout. The PFD, the CP, and the loop filter incorporate actual devices, thus producing a realistic ripple. Figure 13.59(a) shows the simulated settling behavior of the control voltage. The loop locks in about 150 ns, incurring a peak-to-peak ripple of nearly 30 mV [Fig. 13.59(b)]. We observe that our choice of the loop parameters has yielded a well-behaved lock response. This simulation takes about 40 seconds.
Figure 13.59 (a) Simulated transient behavior of scaled PLL design, (b) plot of (a) for a narrower time scale showing the ripple waveform.

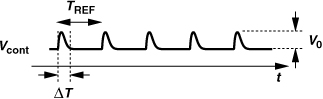
The ripple revealed by the above simulation merits particular attention. Given that the amplitude falls 100-fold in the unscaled loop, we must determine whether the resulting sidebands at ±5-MHz offset have a sufficiently small magnitude. Recall from Chapter 9 that the ripple can be approximated by a train of impulses. In fact, if the area under the ripple is given by, e.g., V0ΔT (Fig. 13.60), then the relative magnitude of the sidebands is equal to V0ΔTKVCO/(2π). In the above simulations, the area under the ripple is roughly equal to 30 mV × 200 ps × 1/2. This value is scaled down by a factor of 100 and multiplied by KVCO/(2π) = 200 MHz/V, yielding a relative sideband magnitude of 6 × 10−4 = −64.4 dBc at the output of the 12-GHz VCO. Thus, the 6-GHz carrier exhibits a sideband around −70 dBc, an acceptable value.
Figure 13.60 Approximation of ripple by impulses.
References
[1] L. L. Kan et al., “A 1-V 86-mW-RX 53-mW-TX Single-Chip CMOS Transceiver for WLAN IEEE 802.11a,” IEEE Journal of Solid-State Circuits, vol. 42, pp. 1986–1998, Sept. 2007.
[2] K. Cai and P. Zhang, “The Effects of IP2 Impairment on an 802.11a OFDM Direct Conversion Radio System,” Microwave Journal, vol. 47, pp. 22–35, Feb. 2004.
[3] I. Vassiliou et al., “A Single-Chip Digitally Calibrated 5.15-5.825-GHz 0.18-?m CMOS Transceiver for 802.11a Wireless LAN,” IEEE Journal of Solid-State Circuits, vol. 38, pp. 2221–2231, Dec. 2003.
[4] C. Rapp, “Effects of HPA-Nonlinearity on a 4-DPSK/OFDM-Signal for a Digital Sound Broadband System,” Rec. Conf. ECSC, pp. 179–184, Oct. 1991.
[5] M. Simon et al., “An 802.11a/b/g RF Transceiver in an SoC,” ISSCC Dig. Tech. Papers, pp. 562–563, (also Slide Supplement), Feb. 2007.
[6] T.-C. Lee and B. Razavi, “A Stabilization Technique for Phase-Locked Frequency Synthesizers,” IEEE Journal of Solid-State Circuits, vol. 38, pp. 888–894, June 2003.
[7] A. Afsahi and L. E. Larson, “An Integrated 33.5 dBm Linear 2.4 GHz Power Amplifier in 65 nm CMOS for WLAN Applications,” Proc. CICC, pp. 611–614, Sept. 2010.
[8] A. Pham and C. G. Sodini, “A 5.8-GHz 47% Efficiency Linear Outphase Power Amplifier with Fully Integrated Power Combiner,” IEEE RFIC Symp. Dig. Tech. Papers, pp. 160–163, June 2006.
[9] B. Chang, J. Park, and W. Kim, “A 1.2-GHz CMOS Dual-Modulus Prescaler Using New Dynamic D-Type Flip-Flops,” IEEE J. Solid-State Circuits, vol. 31, pp. 749–754, May 1996.
Problems
13.1. Repeating the calculations leading to Eq. (13.7), determine the required IIP3 of an 11a/g receiver for a data rate of 54 Mb/s and a sensitivity of −65 dBm.
13.2. Suppose the interferers in Example 13.5 are not approximated by narrowband signals. Is the corruption due to reciprocal mixing greater or less than that calculated in the example?
13.3. Repeat Example 13.5 for the low sensitivity case, i.e., with the desired input at −65 dBm. Assume a noise-to-signal ratio of −35 dB.
13.4. Using the equations derived in Chapter 6 for the input impedance of a single-balanced voltage-driven passive mixer, estimate the load impedance seen by the LNA in Fig. 13.19.
13.5. Two blockers of equal power level appear in the adjacent and alternate adjacent channels of an 11a receiver. If the receiver has a phase noise of −100 dBc/Hz, what is the highest blocker level that allows a signal-to-noise ratio of 30 dB? Neglect other sources of noise.
13.6. Repeat the above problem for only one blocker in the adjacent channel and compare the results.
13.7. Assuming λ > 0, derive the voltage gain and input impedance of the LNA shown in Fig. 13.14(a).
13.8. Determine the noise contribution of I1 and I2 in Fig. 13.26(b) to the input for minimum and maximum gain settings. Neglect the on-resistance of the switches, channel-length modulation, and body effect.
13.9. In the circuit of Fig. 13.44(b), prove that the gain from the noise voltage of each resistor to the VCO output frequency is equal to KVCO.
13.10. Considering the leakage current of the transistors in Fig. 13.50(a), prove that the state eventually vanishes if CK remains low indefinitely. Assuming each output node has a leakage current of I1 and a total capacitance of C1, estimate the time necessary for the state to vanish.