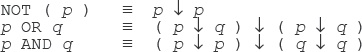First of all, in the body of the chapter I asked which of the following natural language sentences were legal propositions. My own answers are as follows (but some of them might be open to debate):
Bach is the greatest musician who ever lived. Yes.
What’s the time? No. It doesn’t make sense to ask “Is it true that p?” where p is “What’s the time?”
Supplier S2 is located in some city, x. My own answer here is yes, but you might argue reasonably argue that it should be no. In fact, the example is a good illustration of the ambiguity problem discussed earlier in the chapter; my answer is based on the assumption that the phrase “some city, x” could be abbreviated to just “some city” without changing the overall meaning of the sentence,[208] but you might reasonably argue the opposite. Compare and contrast “We both have the same favorite author, x” (see below).
Some countries have a female president. Yes.
All politicians are corrupt. Yes.
Supplier S1 is located in Paris. Yes (though it’s false, given our usual sample values).
We both have the same favorite author, x. No. Here I’m assuming that the phrase “the same favorite author, x” couldn’t be abbreviated to just “the same favorite author” without changing the overall meaning of the sentence (but you could reasonably argue the opposite). If my assumption is correct, then x is a variable (better: a parameter), and until we know what argument is to be substituted for that parameter—i.e., until we know what that x stands for, as it were—we can’t assign a truth value to the sentence. But when we do know—i.e., when we substitute Jane Austen, say, for x—then the sentence does become a proposition.
Nothing is heavier than lead. Yes.
It will rain tomorrow. No. It doesn’t make sense to ask “Is it true that it will rain tomorrow?”—at least, not if you’re expecting an answer (yes or no) that’s guaranteed to be unequivocally correct. Alternatively, we might say that tomorrow here is a variable, and we can’t assign a truth value to the sentence until we know what that variable stands for.
Supplier S6’s city is unknown. Yes. See Appendix C for further discussion of propositions like this one.
10.1 See the answer to Exercise 4.10 earlier in this appendix.
10.2 This is one of De Morgan’s laws. It’s proved in Chapter 11.
10.3 Consider the following truth table:
Since the final column contains T (true) in every position, the given expression is indeed a tautology.
10.4 First of all, it’s easy to see that we don’t need both OR and AND, because
pANDq≡ NOT ( NOT (p) OR NOT (q) )
and
pORq≡ NOT ( NOT (p) AND NOT (q) )
These equivalences are easily established by means of truth tables, as in the answer to Exercise 10.3 above (in fact, the first is the contrapositive of the equivalence—one of De Morgan’s laws—from Exercise 10.2). What they show is that OR and AND can each be defined in terms of the other, together with NOT. It follows that we can freely use both OR and AND in what follows.
Now consider the connectives involving a single proposition p. Let c(p) be the connective under consideration. Then the possibilities are as follows:
c(p) ≡pOR NOT (p)/* always TRUE */c(p) ≡pAND NOT (p)/* always FALSE */c(p) ≡p/* identity */c(p) ≡ NOT (p)/* NOT */
Now consider the connectives involving two propositions p and q. Let c(p,q) be the connective under consideration. Then the possibilities are as follows:
c(p,q) ≡pOR NOT (p) ORqOR NOT (q)c(p,q) ≡pAND NOT (p) ANDqAND NOT (q)c(p,q) ≡pc(p,q) ≡ NOT (p)c(p,q) ≡qc(p,q) ≡ NOT (q)c(p,q) ≡pORqc(p,q) ≡pANDqc(p,q) ≡pOR NOT (q)c(p,q) ≡pAND NOT (q)c(p,q) ≡ NOT (p) ORqc(p,q) ≡ NOT (p) ANDqc(p,q) ≡ NOT (p) OR NOT (q)c(p,q) ≡ NOT (p) AND NOT (q)c(p,q) ≡ ( NOT (p) ORq) AND ( NOT (q) ORp)c(p,q) ≡ ( NOT (p) ANDq) OR ( NOT (q) ANDp)
As a subsidiary exercise, and in order to convince yourself that the foregoing definitions do indeed cover all of the possibilities, you might like to construct the corresponding truth tables (and compare them with those given in the answer to Exercise 4.10 earlier in this appendix).
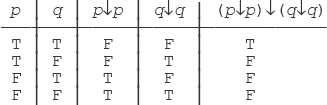
Turning to part (b) of the exercise: Actually there are two such primitives, NOR and NAND, often denoted by a down arrow, “↓” (the Peirce arrow) and a vertical bar, “|” (the Sheffer stroke), respectively. Here are the truth tables:
As these tables suggest, p↓q (“p NOR q”) is equivalent to NOT (p OR q) and p|q (“p NAND q”) is equivalent to NOT (p AND q). In what follows, I’ll concentrate on NOR (I’ll leave NAND to you). Observe that this connective can be thought of as “neither nor” (“neither the first operand nor the second is true”). I now show how to define NOT, OR, and AND in terms of this operator:
For example, let’s take a closer look at the case of p AND q (I’ll leave the NOT(p) and p OR q cases to you):
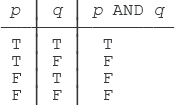
This truth table shows that (p↓p)↓(q↓q) is equivalent to p AND q, because its first, second, and final columns are identical to the corresponding columns in the truth table for AND:
Since we’ve already seen that all of the other connectives can be expressed in terms of NOT, OR, and AND, the overall conclusion follows.
10.5 (a) “The sun is a star” and “the moon is a star” are both propositions, though the first is true and the second false. (b) The sun satisfies the predicate, the moon doesn’t.
10.6 This exercise points up the question of ambiguity once more. If the predicate means x has exactly two moons, then clearly Jupiter doesn’t satisfy it. But if it means x has at least two moons (and maybe more), then Jupiter does satisfy it. Once again, then, we see how logic forces us—or does its best to force us, at any rate—into thinking clearly and saying exactly what we mean.
10.7 A parameter can be replaced by any argument whatsoever, just so long as it’s of the right type. A designator isn’t, and in fact can’t be, replaced by anything at all; instead—just like a variable reference in a programming language, in fact—it simply “designates,” or denotes, the value of the pertinent variable at the pertinent time (i.e., when the constraint is checked, in the case at hand).
10.8 “Get names of suppliers such that there exists a shipment—a single shipment, that is—that links them to every part.” The query probably isn’t very sensible; note that it will return either (a) all supplier names if the cardinality of relvar P is less than two or (b) an empty result otherwise.
10.9 The following SQL expressions are deliberately meant to be as close to their relational counterparts (as given in the body of the chapter) as possible. See Chapter 11 for further discussion.
Example 1: Get all pairs of supplier numbers such that the suppliers concerned are colocated.
SELECT SX.SNO AS SA , SY.SNO AS SB FROM S AS SX , S AS SY WHERE SX.CITY = SY.CITY AND SX.SNO < SY.SNO
Example 2: Get supplier names for suppliers who supply at least one red part.
SELECT DISTINCT SX.SNAME
FROM S AS SX
WHERE EXISTS
( SELECT *
FROM SP AS SPX
WHERE EXISTS
( SELECT *
FROM P AS PX
WHERE PX.COLOR = 'Red'
AND SX.SNO = SPX.SNO
AND SPX.PNO = PX.PNO ) )Example 3: Get supplier names for suppliers who supply at least one part supplied by supplier S2.
SELECT DISTINCT SX.SNAME
FROM S AS SX
WHERE EXISTS
( SELECT *
FROM SP AS SPX
WHERE EXISTS
( SELECT *
FROM SP AS SPY
WHERE SX.SNO = SPX.SNO
AND SPX.PNO = SPY.PNO
AND SPY.SNO = 'S2' ) )Example 4: Get supplier names for suppliers who don’t supply part P2.
SELECT DISTINCT SX.SNAME
FROM S AS SX
WHERE NOT EXISTS
( SELECT *
FROM SP AS SPX
WHERE SPX.SNO = SX.SNO
AND SPX.PNO = 'P2' )Example 5: For each shipment, get full shipment details, including total shipment weight.
SELECT SPX.* , PX.WEIGHT * SPX.QTY AS SHIPWT FROM P AS PX , SP AS SPX WHERE PX.PNO = SPX.PNO
Example 6: For each part, get the part number and the total shipment quantity.
SELECT PX.PNO , ( SELECT COALESCE ( SUM ( SPX.QTY ) , 0 )
FROM SP AS SPX
WHERE SPX.PNO = PX.PNO ) AS TOTQ
FROM P AS PXExample 7: Get part cities that store more than five red parts.
SELECT DISTINCT PX.CITY
FROM P AS PX
WHERE ( SELECT COUNT ( * )
FROM P AS PY
WHERE PY.CITY = PX.CITY
AND PY.COLOR = 'Red' ) > 510.10 The following truth table shows (how, exactly?) that AND is associative; the proof for OR is analogous.
Note: The formal name for AND is conjunction, and its operands (i.e., the terms being ANDed together) are called conjuncts. Similarly, the formal name for OR is disjunction, and its operands are called disjuncts. Further, since (a) AND and OR are commutative as well as associative and (b) they both possess an identity value, we can define n-adic versions, as follows:
AND {p1,p2,...,pn} is defined to be equivalent to
(
p1) AND (p2) AND ... AND (pn) AND TRUEIf none of the p’s involves any ANDs, this expression overall is said to be in conjunctive normal form (CNF).
OR {p1,p2,...,pn} is defined to be equivalent to
(
p1) OR (p2) OR ... OR (pn) OR FALSEIf none of the p’s involves any ORs, this expression overall is said to be in disjunctive normal form (DNF).
10.11 a. Not valid (suppose x ranges over an empty set and q is TRUE; then EXISTS x (q) is FALSE). b. Not valid (suppose x ranges over an empty set and q is FALSE; then FORALL x (q) is TRUE). c. Valid. d. Valid. e. Not valid (suppose x ranges over an empty set; then FORALL x (p(x)) is TRUE but EXISTS x (p(x)) is FALSE, and TRUE ⇒ FALSE is FALSE). f. Not valid (suppose x ranges over an empty set; then EXISTS x (TRUE) is FALSE). g. Not valid (suppose x ranges over an empty set; then FORALL x (FALSE) is TRUE). h. Valid. i. Not valid (e.g., the fact that exactly one integer is equal to zero doesn’t imply that all integers are equal to zero). j. Not valid (e.g., the fact that all days are 24 hours long and the fact there exists at least one day that’s 24 hours long don’t together imply that exactly one day is 24 hours long). k. Valid. Note: (Valid!) equivalences and implications like those under discussion here (and in the next exercise) can be used as a basis for a set of calculus expression transformation rules, much like the algebraic expression transformation rules discussed in Chapter 6. See Chapter 11 for further discussion.
10.12 a. Valid. b. Valid. c. Valid. d. Valid. e. Not valid (e.g., saying that for every integer y there exists a greater integer x isn’t the same as saying there exists an integer x that’s greater than all integers y). f. Valid.
10.13 I give solutions only where there’s some significant point to be made regarding the solution in question. For cross reference purposes, I show the numbers of the original exercises in italics. Exercises from Chapter 6:
6.12 The following relational calculus expressions denote TABLE_DEE and TABLE_DUM, respectively:
{ } WHERE TRUE
{ } WHERE FALSEAnd this expression denotes the projection of the current value of relvar S on no attributes:
{ } WHERE EXISTS ( SX )The relational calculus isn’t usually considered as having a direct counterpart to Tutorial D’s r{ALL BUT ...}, but there’s no reason in principle why it shouldn’t.
6.15 The relational calculus isn’t usually considered as having a direct counterpart to Tutorial D’s D_UNION or I_MINUS, but there’s no reason in principle why it shouldn’t.
10.13 (cont.) Exercises from Chapter 7:
7.1
d. { PX } WHERE SUM ( SPX WHERE SPX.PNO = PX.PNO , QTY ) < 500
e. { PX } WHERE EXISTS ( SX WHERE SX.CITY = PX.CITY )
j. { PX , SCT := COUNT ( SPX WHERE SPX.PNO = PX.PNO ) }
7.8 A relational calculus analog of the Tutorial D expression SP GROUP ({} AS X) is:
{ SPX , X := { } }7.11 { SX , PNO_REL := { SPX.PNO } WHERE SPX.SNO = SX.SNO }
7.12 In practice we need analogs of the conventional INSERT, DELETE, and UPDATE (and relational assignment) operators that are in keeping with a calculus style rather than an algebraic one (and this observation is true regardless of whether we’re talking about relvars with RVAs, as in the present context, or without them). Further details are beyond the scope of the present book, but in any case are straightforward. No further answer provided.
10.13 (cont.) Exercises from Chapter 8: No answers provided.
10.13 (cont.) Exercises from Chapter 9: No answers provided.
10.14 Recall from the body of the chapter that the set over which a range variable ranges is always the body of some relation—usually but not always the relation that’s the current value of some relvar (emphasis added). In this example, the range variable ranges over what is, in effect, a union:
RANGEVAR CX RANGES OVER { SX.CITY } , { PX.CITY } ;
{ CX } WHERE TRUENote that the definition of range variable CX makes use of range variables SX and PX, which I assume to have been previously defined.
10.15 In order to show that SQL is relationally complete, it’s sufficient to show that (a) there exist SQL expressions for each of the algebraic operators restrict, project, product, union, and difference (because as we saw in Chapter 6, all of the other algebraic operators discussed in this book can be defined in terms of these five),[209] and (b) the operands to those SQL expressions can be arbitrarily complex SQL expressions in turn. So let’s try.
First of all, as we know, SQL effectively does support the relational algebra RENAME operator, thanks to the availability of the optional AS specification on items in the SELECT clause.[210] We can therefore ensure that tables do all have proper column names, and hence that the operands to product, union, and difference in particular satisfy the requirements of the algebra with respect to column naming. Furthermore—provided those column naming requirements are indeed satisfied—the SQL column name inheritance rules in fact coincide with those of the algebra as described in Chapter 6.
Here then are SQL expressions corresponding approximately to the five primitive operators mentioned above:
Moreover, (a) R, R1, and R2 in the SQL expressions shown above are all table expressions (in the sense in which I’ve been using this latter term throughout this book up to this point), and (b) if we take any of those expressions and enclose it in parentheses, what results is a table expression in turn.[211] It follows that SQL is indeed relationally complete. Or is it? Unfortunately, the answer is no. The reason is that there’s a slight (?) glitch in the foregoing argument—SQL fails to support projection on no columns at all, because it doesn’t support empty commalists in the SELECT clause. As a consequence, it doesn’t support TABLE_DEE or TABLE_DUM, and therefore it isn’t relationally complete after all ... but it “nearly” is.
10.16 Let TP and DC denote the propositions “the database contains only true propositions” and “the database is consistent,” respectively. Then the first bullet item says:
IFTPTHENDC
The second says:
IF NOT (DC) THEN NOT (TP)
And it’s easy to see that these two propositions are indeed equivalent (in fact, each is the contrapositive of the other).
10.17 No, it isn’t—though textbooks on logic usually claim the opposite, and in practice it’s “usually” achievable. Here’s an example of a relational calculus expression where the predicate in the WHERE clause can’t be replaced by a PNF equivalent:
SX WHERE EXISTS SPX ( SPX.SNO = SX.SNO ) OR SX.CITY = 'Athens'
The paper “A Remark on Prenex Normal Form” (see Appendix G) explains the situation in detail.
[208] In other words, x here is a bound variable, and the sentence could be rephrased thus: “There exists some city, say x, such that supplier S2 is located in city x.”
[209] Except for TCLOSE—but TCLOSE wasn’t included in the original definition of what it meant to be relationally complete, anyway. Note: You might be wondering about some of the other operators from Chapter 7 (e.g., EXTEND, SUMMARIZE, and GROUP and UNGROUP). In fact, Hugh Darwen and I show in our book Databases, Types, and the Relational Model: The Third Manifesto (see Appendix G) that these operators can indeed be defined in terms of restrict, project, etc.
[210] To state the matter a little more precisely: An SQL analog of the algebraic expression R RENAME {A AS B} is the (extremely inconvenient!) SQL expression SELECT X, Y, ..., Z, A AS B FROM R (where X, Y, ..., Z are all of the columns of R apart from A, and I choose to overlook the fact that the SQL expression results in a table with a left to right ordering to its columns).
[211] I choose to overlook the fact that SQL would actually require such a table expression, when used in any of the contexts under discussion, to be accompanied by a pointless range variable definition.