and
Thus, (u∗, w∗) is a critical point of E T(u, w) since it fulfills the Euler–Lagrange equations. Because of the convexity of the functional in one variable whenever the other one is fixed, we have that (u∗, w∗) actually is a local minimizer. The stated space inclusions hold due to the estimates shown in Proposition 4.1 (see Remark 4.5).
4.4.1.4.2 T = 0
For E0, as we have discussed before, and as can be seen in [4, Thm. 2], we are lacking information on the compactness of the iterates. Thus, the convergence of the alternating minimization scheme in the one-to-one correspondence model can not be proven in the continuous case by compactness arguments. One way of regaining compactness is to restrict the model to (finite dimensional) sampled images by means of a proper discretization. We may therefore restrict ourselves to a finite number Nθ of admissible rotation angles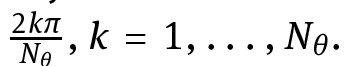 
We define 
For acertain grid constant τ > 0 we set
P ̃ = Õ ∩ τℤ2 ,
P̃ c = Õ c ∩ τℤ2 .
We note that û is considered to be a function on Õ c, such that the evaluation for y ∈Õ c P̃ c still makes sense.
In general, also for the continuous case, we consider the following alternating minimization algorithm:
Algorithm 4.11 (Alternated minimization of E0). Initialization: choose u0 with ‖u0‖∞ ≤ ‖û‖∞ For k ∈ ℕ solve
As discussed before, we can set νk to be the measure which is induced by the measurable one-to-one correspondence map φ: P ̃ → P̃ c × M θthat maps x to (y, θ) such that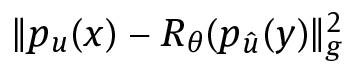 
is minimal for each x ∈ P̃. Further, for x ∈ P ̃ we have the discrete minimizer of (4.46) can be computed by (see also (4.7))
In general, we have the following convergence result, which can be adapted to the discrete and finite dimensional setting where actually compactness is guaranteed.
Proposition 4.12. Assume that the sequence (uk , wk) generated by the algorithm is actually compact in A0.(Let us stress that in the discrete case this assumption is validated, while for the continuous setting the compactness of the sequence is an open issue.) Then its limits are critical points of the energy E 0.
Proof. Since uk and νk are bounded there exists a subsequence (ukj , νkj ) converging to (ū , ν̄). Then clearly, by the definition, ν̄ is a minimizer of ν ↦ E 0(ū, ν). We will now show that ukj+1 − ukj converges to zero.
The sequence (E0(uk , νk))k∈ℕ, obtained from the alternating minimization scheme on E 0(u, ν), is monotonically decreasing and bounded below because E 0(u, w) ≥ 0 for all (u, w) ∈ ?0 and hence a convergent sequence. Furthermore, since E 0(uk , νk) ≥ E0(uk+1, νk) ≥ E0(uk+1, νk+1), we have that
We rewrite E0(uk , νk) − E0(uk+1, νk) with the notation z = (y, θ), ? = Õ × Õ c × [0, 2π], uk = uk(x + h), likewise for uk+1, ûθ = û(y + rθ(h)) and work in the integral notation for better readability:
The first term on the right-hand side is zero due to the fact that uk+1 is the minimizerof E0(u, νk) with νk fixed and since 2 ∫?∫ℝ2 g(h)(ûθ − uk+1)(uk+1 − uk)dhdνk(x, z) isprecisely the variational derivative of E0 at (uk+1, νk) and in direction uk+1 − uk. Wemay proceed as in (3.3) and (3.4) to obtain that for almost every x the following estimateholds:
due to the radial symmetry of g, the fact that ∫ℝ2 g(h)dh = 1, and the fact that νx is a probability density for all x ∈ O. Thus, in view of (4.48) and (4.49), uk+1 −uk converges to zero as k → 0, and in particular ukj+1 − ukj converges to zero as kj → 0. We proceed as in the proof of Proposition 4.10 to obtain equations similar to (4.43) and (4.44) and deduce that ū is a minimizer of E 0(u, ν̄) with ν̄ fixed. Hence (ū, ν̄) is a local minimizer of E0(u, ν).
4.4.2Analysis of E∇,T
We will now analyze the functional E∇,T, for T > 0. We will show the existence of minimizers and examine their properties. Thereafter, we will show convergence of the alternated optimization scheme.
Let us consider the functional of the patch non-local Poisson model
We define the set of admissible function pairs (u, w) based on definition of ? in (4.8) from Section 4.4.1.2:
We recall the Euler–Lagrange equations which were derived in Section 4.3.2.2. The minimizer E∇,T(u, ⋅) for fixed u is given by
where
is the normalization to make w a probability density (to fulfill (4.51)).
For a fixed w and minimizing with respect to u we obtain
where
4.4.2.1Existence of minimizers
In this section we shall prove the existence of minimizers to the following minimization problem:
Proposition 4.13. Assume that u ̂ ∈W2,2(Oc) ∩ W1,∞(Oc) ∩ L∞(Oc) and g ∈ W1,∞(ℝ2, ℝ+) has compact support in Ωp = Br(0) and is radially symmetric, that is g(h) = g(|h|). Then there exists a solution to thevariational problem (4.57). Moreover, for any solution (u, w) of (4.57) we have u ∈ W1,2(O) ∩ 
(O) ∩ L∞(O) for all p ∈ [0,∞) and w ∈ W1,∞(Õ × Õ c × [0, 2π]).
For the proof of Proposition 4.13 we need the following two lemmas.
Lemma 4.14. Assume that u ̂ ∈ W1,∞(Oc) and g as in Proposition 4.13. Let (u, w) ∈ ?∇ and E∇,T(u, w) ≤ C. Then
Proof. Let us first note that for a, b ∈ ℝm and any ε > 0
since 
By assumption, we have that E∇,T(u, w) ≤ C and thus exists C1 = C1(C) > 0 suchthat
We rewrite the term on the left-hand side and use (4.59) with 
to estimate that
where 
dθdydx is bounded by a constant depending on ‖w‖L1 and ‖∇û‖∞.
which concludes the proof.
Lemma 4.15. Assume that û ∈ W2,2(Oc), u ∈ W1,2(O), u|∂O = û|∂Oc and g as above.Then
are bounded in L∞(Õ × Õ c × [0, 2π]).
Proof. Let us write ui(x) = ∂xi u(x), û i(x) = ∂xi û(x), i = 1, 2. Then for i ∈ {1, 2} we have
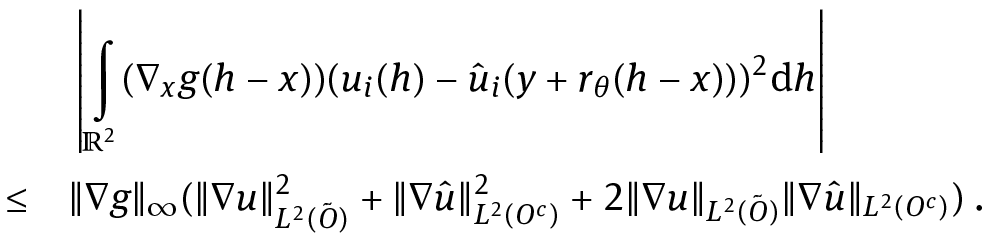
The second term on the right-hand side in (4.64) is estimated as follows:
Finally, for the last term on the right-hand side of (4.64) we have
Now let ξ ∈ {y, θ} and i ∈ {1, 2}. Then
We are now in a position to prove Proposition 4.13.
Proof of Proposition 4.13. Let (un, wn) be a minimizing sequence of (4.57). We proceed as in the proof of Proposition 4.1: Since Ω is a bounded domain, we have that
is bounded. Hence by [2, Prop. 1.27] (wn)n∈ℕ is equi-integrable. Then we apply the Dunford–Pettis theorem to obtain that (wn)n∈ℕ is relatively weakly compact in L1. We deduce a subsequence exists, again denoted by wn, which weakly converges in L1(Õ × Õ c × [0, 2π]) to some w ∈ ?. By Lemma 4.14, we have that un is uniformly boundedin W1,2(Õ ). By Lemma 4.15, we have that ∇ξ ∫ℝ2 |∇hu(x + h) − ∇hû(y + rθ(h))|2g(h)dh, ξ = x, y, θ, are uniformly bounded in L1(Õ × Õ ×[0, 2π]). Hence a subsequence exists, again denoted by un, which is such that un → u almost everywhere and in L2(Õ ), ∇un → ∇u weakly in L2(Õ ) and, by the theorem of Ascoli–Arzelá, ∫ℝ2 g(h)(∇hun(x +h) − ∇hû(y + rθ(h)))2dh converges uniformly to some function W(x, y, θ).
By the same argumentation as in the proof of Proposition 4.1, using Mazur’s Lemma,we obtain an estimate like the one in (4.25) and deduce for n →∞that
Proceeding as in (4.26) we deduce that
To prove that 
and w ∈ W1,∞(Õ × Õ c × [0, 2π]), let (u, w) ∈ ?∇ be a solution to the variational problem (4.57). Then, by Lemma 4.14, u ∈ W1,2(O), and since (u, w) is the minimizer of E∇,T the Euler– Lagrange equations (4.53) and (4.55) are satisfied. Then in particular u is a solution of the Poisson equation:
where
Furthermore, w fulfills
where the normalization factor Z∇,T(u)(x) is given by
As in the proof of Proposition 4.1 we observe that Z∇,T(u)(x) is bounded and bounded away from zero by Lemmas 4.14 and 4.15.With equations similar to (4.29), (4.30), and (4.31) we obtain that w ∈ W1,∞(Õ × Õ c × [0, 2π]). With this result and (4.69) we havethat υ(w) ∈ W1,∞(O)2. Then the solution u of (4.68) is in 
for any p ∈ [0, ∞), cf. [4, 33].
Remark 4.16. Notice that if a pair (u, w) ∈ ?∇ fulfills (4.53) and (4.55) and if E∇,T(u, w) ≤ C < ∞then w ∈ W1,∞(Õ × Õ c × [0, 2π]) and 
for any p ∈ [0, ∞).
4.4.2.2Convergence of the alternated minimization scheme
In this section we shall prove the convergence of the alternated optimization scheme for E∇,T, T > 0, described in Algorithm 4.17. As is the case for ET, T > 0, the presented results hold in the continuous and discrete setting.
Algorithm 4.17 (Alternated minimization of E∇,T). Initialization: choose u0 with ‖u0‖∞ ≤ ‖û‖∞ For k ∈ ℕ solve
Under the assumptions made in Proposition 4.13 one may show the following result:
Proposition 4.18. The iterated optimization algorithm converges (modulo a subsequence) to a critical point (u∗, w∗) ∈ ?∇ of the energy ET. The solution obtained satisfies the regularity properties stated in Proposition 4.13, that is u∗ ∈ W1,2(O) ∩ 
(O) ∩ L∞(O) for all p ∈ [0,∞) and w∗ ∈ W1,∞(Õ × Õ c × [0, 2π]).
Proof. Let us show that wk is bounded and bounded away from zero independently of k: Since wk fulfills the Euler–Lagrange equation we have that
where the normalization factor Z∇,T(uk−1)(x) is given by
By Lemma 4.14 uk is uniformly bounded in W1,2(O) such that 
is uniformly bounded by Lemma 4.15. Therefore exist constants b > a > 0 and c > 0 which are independent of k such that
and for any choice of (x, y, θ) ∈ Õ × Õ c × [0, 2π]
By equations similar to (4.29), (4.30), and (4.31),we have that wk is uniformly boundedin W1,∞(Õ × Õ c × [0, 2π]). Thus, we may extract a subsequence wkj which weakly converges to some w∗ in Lp for all p ∈ [1, ∞] and ukj converges weakly to some u∗ ∈ W1,2(O).
With a similar argument as in the proof of Proposition 4.10 we obtain
where γ > 0, and deduce that 
Hence also wkj+1 weakly convergesto w∗ in Lp for all p ∈ [1, ∞].
As kj →∞we have that
and hence (u∗, w∗) ∈ ?∇ is a critical point of E∇,T, such that u∗ is a solution to the Euler–Lagrange equation (4.55) and w∗ is a solution to the Euler–Lagrange equation (4.53). By Remark 4.16 we have the stated regularity.
4.4.3Conclusion and future perspectives
In this work a variational framework for exemplar-based image inpainting under rotation invariance of the exemplar patches was presented. The framework is both suited to the case of one-to-one correspondences and probabilistic correspondences. For the application to image inpainting problems the one-to-one correspondences model proves to be more relevant. However, the given framework shows the connections to other fields in mathematical imaging, namely image denoising and regularization and provides a basis for unified treatment.
The newly introduced L2-based error functions which incorporate the rotation invariance of the exemplar patches can be computed using tools which were developed in this work and be efficiently implemented by FFT-based convolutions.
Let us now briefly depict possible practical and theoretical extensions to the work presented herein.
4.4.3.1Color images
For the treatment of inpainting problems on color images, one shall define error functions for color patches as the sum of the three scalar components:
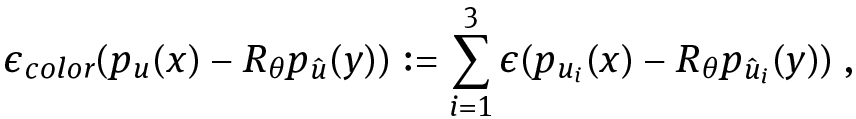
where u : Ω → ℝ3 denotes the color image with three different color channels ui. The scalar error function ϵ can for instance be chosen as one of the rotation invariant patch error functions introduced in Section 4.2.1. This choice of color error function ensures that the image update in the corresponding Euler–Lagrange equation is accomplished with one correspondence map for all three channels at the same time, and hence the inpainting information of the three color channels are matching.
4.4.3.2Combining error functions
Once the rotation invariant inpainting algorithms are implemented, one can try to combine the patch non-local means and the patch non-local Poisson scheme to take advantage of the advantages of both methods. Controlled by a parameter λ one can examine the quality of the results of convex combinations ϵλ of the two error functions ϵNLmeans (2.2) and ϵNLPoisson (2.3), that is
In an analysis of this matter [5] suggest a convex combination parameter of λ ∼ 0.1.
4.4.3.3Multiscale schemes
Exemplar-based inpainting methods heavily depend on the size of the patch which is used for the reconstruction, as we have seen in Section 4.3.3. Also, the critical point to which the alternated optimization scheme converges is in general only a local minimizer. A heuristic to avoid local minimizers is to use a multiscale scheme. The motivation is that this helps to find a good initialization at the finest scale and therefore might even save computational cost (Section 4.3.3). At the same time images often contain structures of different sizes (large structures and detailed textures). The multiscale scheme incorporates the search over matching structures of different scale and thus can reproduce these structures properly. Moreover, multiscale schemes are a common approach in exemplar-based inpainting, cf. [5, 38, 56].
4.4.3.4Analysis
As we have stated before, the ability of exemplar-based inpainting algorithms to reconstruct structures without exemplars is not well understood. Motivated by this problem we have introduced the possible rotation of patches to increase the quality of available patches. Clearly, for certain inpainting problems this helps to nicely reconstruct the image, see Section 4.3.3. In a next step, one should try to quantify the benefit of having the possibility to rotate patches on the capability to reconstruct structures in the image. First steps into this direction could be geared to the approach of comparing different inpainting models in [8, Section 7].
Furthermore, an analysis of the patch non-local Poisson scheme for T = 0 should be finalized. This should include a proof of existence of minimizers and convergence results for following the functional
where
Using similar tools as in the proofs of the functionals E0 and E∇,T, T > 0, it should be possible to prove corresponding results for the above model.
Acknowledgment: The authors acknowledge the support of the START Project “SparseApproximation and Optimization in High-Dimensions”.
The authors thank the Johann Radon Institute for Computational and Applied Mathematics (RICAM) for their hospitality during the preparation of this work.
Bibliography
[1]C. D. Aliprantis and K. C. Border. Infinite dimensional analysis: a hitchhiker’s guide. Springer-Verlag, Berlin, Heidelberg, third edition, 2006.
[2]L. Ambrosio, N. Fusco, and D. Pallara. Functions of bounded variation and free discontinuity problems. Oxford University Press, USA, 2000.
[3]G. Arfken. Convolution Theorem. In Mathematical methods for physicists, §15.5, pp. 810–814, Academic Press, Orlando, Florida, third edition, 1985.
[4]P. Arias, G. Facciolo, and V. Caselles. Analysis of a variational framework for exemplar-basedimage inpainting. Technical Report, University Pompeu Fabra, available at http://gpi.upf.edu/static/vnli/vnli-analysis-preprint.pdf, 2011.
[5]P. Arias, G. Facciolo, V. Caselles, and G. Sapiro. A variational framework for exemplar-based image inpainting. International Journal of Computer Vision, 93:319–347, 2011.
[6]H. H. Arsenault and Y. Sheng. Properties of the Circular Harmonic expansion for rotation invariant pattern recognition. Appl. Opt., 25(18):3225–3229, 1986.
[7]G. Aubert and P. Kornprobst. Mathematical problems in image processing. Partial differential equations and the calculus of variations. Springer, Applied Mathematical Sciences, vol. 147, 2006.
[8]J.-F. Aujol, S. Ladjal, and S. Masnou. Exemplar-based inpainting from a variational point of view. SIAM J. Math. Anal., 42(3):1246–1285, 2010.
[9]S. P. Awate and R. T. Whitaker. Higher-order image statistics for unsupervised, informationtheoretic, adaptive, image filtering. Computer Vision and Pattern Recognition, 2:44–51, 2005.
[10]W. Baatz, M. Fornasier, P. Markowich, and C.-B. Schönlieb. Inpainting of ancient Austrian frescoes. In Conference proceedings of Bridges 2008, pp. 150–156, Leeuwarden, 2008.
[11]C. Barnes, E. Shechtman, A. Finkelstein, and D. B. Goldman. PatchMatch: a randomized correspondence algorithm for structural image editing. In Proc. of SIGGRAPH, pp. 1–11, New York,NY, USA, 2009.
[12]C. Barnes, E. Shechtman, D. B. Goldman, and A. Finkelstein. The generalized PatchMatch correspondence algorithm. In European Conference on Computer Vision, 2010.
[13]M. Bertalmío, G. Sapiro, V. Caselles, and C. Ballester. Image inpainting. In Proc. of SIGGRAPH, 2000.
[14]Z. W. Birnbaum and W. Orlicz. Über die Verallgemeinerung des Begriffes der zueinander Konjugierten Potenzen. Studia Mathematica, 3:1–67, 1931 (in German).
[15]F. Bornemann and T. März. Fast image inpainting based on coherence transport. Journal of Mathematical Imaging and Vision, 28(3):259–278, 2007.
[16]A. Buades, B. Coll, and J.-M. Morel, A review of image denoising algorithms, with a new one. Multiscale Model. Simul., 4(2):490–530, 2005.
[17]V. Caselles, J.-M. Morel, and C. Sbert. An axiomatic approach to image interpolation. IEEE Trans. Image Processing, 7(3):376–386, 1998.
[18]R. Cazzato, G. Costa, A. D. Farra, M. Fornasier, D. Toniolo, D. Tosato, and C. Zanuso. Il progetto Mantegna – storia e risultati. In Andrea Mantegna. La Cappella Ovetari a Padova (A.M. Spiazzi, A. D. N. Salmazo, D. Toniolo eds.), Skira, 2006 (in Italian).
[19]T. F. Chan and J. Shen. Mathematical models for local non-texture inpaintings. SIAM J. Appl. Math., 62(3):1019–1043, 2001.
[20]L. Chanas, J. P. Cocquerez, and J. Blanc-Talon. Simultaneous inpainting and motion estimation of highly degraded video-sequences. Lecture Notes in Computer Science, 2749:11–23, 2003.
[21]A. Criminisi, P. Perez, and K. Toyama. Region filling and object removal by exemplar-based inpainting. IEEE Trans. on Image Processing, 13(9):1200–1212, 2004.
[22]L. Demanet, B. Song, and T. Chan. Image inpainting by correspondence maps: a deterministic approach. Applied and Computational Mathematics, 1100:217–250, 2003.
[23]I. Ekeland and R. Témam. Convex analysis and variational problems. SIAM, Philadelphia, 1999. Republication of North-Holland and American Elsevier, Amsterdamand New York, 1976.
[24]M. Elad, J.-L. Starck, P. Querre, and D. L. Donoho. Simultaneous cartoon and texture image inpainting using morphological component analysis. Applied and Computational Harmonic Analysis, 19(3):340–358, 2005.
[25]M. Eller, Rotation Invariance in Exemplar-based Image Inpainting, Master Thesis, Technische Universität München, August 31, 2013.
[26]G. Émile-Mâle. The Restorer’s Handbook for Easel Painting. Van Nostrand Reinhold, New York, 1976.
[27]A. A. Eufros and T. K. Leung. Texture synthesis by non-parametric sampling. In Proc. of the IEEE Conf. on CVPR, pp. 1033–1038, Corfu, Greece, September 1999.
[28]H. G. Feichtinger and T. Strohmer. Gabor Analysis and algorithms. Birkhäuser Verlag, Basel, 1998.
[29]M. Fornasier. Un metodo per la rappresentatione ed il confronto di immagini a meno di rotazione. Laurea thesis, University of Padova, October 1999 (in Italian).
[30]M. Fornasier. Decomposition of Hilbert spaces: local construction of global frames. In B. Bojanov (Ed.): Proc. of the Int’l Conf. on Constructive theory of functions, Varna 2002, pp. 275–281, DARBA, Sofia, 2003.
[31]M. Fornasier. Function spaces inclusions and rate of convergence of Riemann-type sums in numerical integration. Numer. Funct. Anal. Optim., 24(1–2):45–57, 2003.
[32]M. Fornasier and D. Toniolo. Fast, robust and efficient 2D pattern recognition for re-assembling fragmented images. Pattern Recognition, 38:2074–2087, 2005.
[33]D. Gilbarg and N. S. Trudinger. Elliptic partial differential equations of second order. Springer-Verlag, Berlin, Heidelberg, 2001.
[34]G. Gilboa and S. Osher. Nonlocal operators with applications to image processing. Multiscale Modeling and Simulation, 7(3):1005–1028, 2008.
[35]J.-W. Gu, L. Zhang, G.-Q. Yu, Y.-X. Xing, and Z.-Q. Chen. X-ray CT metal artifacts reduction through curvature based sinogram inpainting. Journal of X-Ray Science and Technology, 14(2):73–82, 2006.
[36]F. Hecht. FreeFem++ Documentation, Version 3.22. Available at http://www.freefem.org/ff++/ftp/freefem++doc.pdf.
[37]H. Igehy and L. Pereira. Image replacement through texture synthesis. In Proc. of the IEEE Conf. on CVPR, October 1997.
[38]N. Kawai, T. Sato, and N. Yokoya. Image inpainting considering brightness change and spatiallocality of textures and its evaluations. In Ad. in Image and Video Tech., pp. 271–282, Springer-Verlag, Berlin, Heidelberg, 2009.
[39]C. Kervrann and J. Boulanger. Local adaptivity to variable smoothness for exemplar-based image regularization and representation. International Journal of Computer Vision, 79(1):45–69, 2008.
[40]S. Kindermann, S. Osher, and P. W. Jones. Deblurring and denoising of images by nonlocal functionals. SIAM Mult. Model. and Simul., 4(4):1091–1115, 2005.
[41]O. Kleinschmidt, T. Brox, and D. Cremers. Nonlocal texture filtering with efficient tree structuresand invariant patch similarity measures. In Int. Workshop on Local and Nonlocal Approximation, 2008.
[42]A. C. Kokaram, R.D. Morris, W. J. Fitzgerald, and P. J.W. Rayner. Detection of missing data in sequences, IEEE Transactions on Image Processing, 11(4):1496–1508, 1995.
[43]M. A. Krasnoselskii and Y. B. Rutickii. Convex functions and Orlicz spaces. P. Noordhoff, Groningen, 1961 (Translation from Russian original).
[44]E. Levina and P. Bickel. Texture synthesis by non-parametric resampling of random fields. Annals of Statistics, 34(4):1751–1773, 2006.
[45]S. Masnou and J. Morel. Level Lines based disocclusion. In 5th IEEE Int’l Conf. on Image Processing, pp. 259–263, Chicago, IL, October 1998.
[46]D. P. Mitchell and A. N. Netravali. Reconstruction filters in computer-graphics. In Proceedingsof ACM SIGGRAPH International Conference on Computer Graphics and Interactive Techniques, 22(4):221–228, 1988.
[47]G. Peyré, S. Bougleux, and L. D. Cohen. Non-local Regularization of Inverse Problems. Inverse Problems and Imaging, 5(2):511–530, 2011.
[48]H. Poppe. Compactness in general function spaces. Dt. Verl. d. Wiss., Berlin, 1974.
[49]C.-B. Schönlieb. Modern PDE techniques for image inpainting. PhD thesis, University of Cambridge, June 2009.
[50]C. E. Shannon. A mathematical theory of communication. The Bell System Technical Journal, 27:379–423, 1948.
[51]C. E. Shannon. Communication in the presence of noise. Proceedings of the IEEE, 86(2):447–457, 1998 (reprint of Proceedings of the IRE, 37(1):10–21, 1949).
[52]A. Szlam, M. Maggioni, and R. R. Coifman. Regularization on graphs on graphs with functionadapted diffusion processes. J. Mach. Learn. Res., 9:1711–1739, 2008.
[53]D. Tschumperlé and R. Deriche. Vector-valued image regularization with PDEs: a common framework for different applications. In Proc. of the IEEE Conf. on CVPR, June 2003.
[54]G. N. Watson. Theory of Bessel functions. Cambridge University Press, Cambridge, 1966.
[55]L.-Y. Wei and M. Levoy. Fast texture synthesis using tree-structured vector quantization. In Proc. of SIGGRAPH, 2000.
[56]Y. Wexler, E. Shechtman, and M. Irani. Space-time completion of video. IEEE Trans. on PAMI, 29(3):463–476, 2007.
[57]K. B. Wolf. Integral transforms in science and engineering. Plenum Press, New York, London, 1979.
[58]X. Zhang, M. Burger, X. Bresson, and S. Osher. Bregmanized nonlocal regularization for deconvolution and sparse reconstruction. CAM Report, 09-03, 2009.