10.1Introduction

The study of periodic trajectories for the Hamiltonian system represents a longstanding problem in dynamical systems and has attracted the interest of many researches, in particular for the N-body problem. The well-known Lyapunov–Poincaré theorem (cf. [6]) establishes, under suitable assumptions, the existence of a one-parameter family of periodic trajectories emanating from a given equilibrium point. The proof is based on the continuation method and leads to obtain periodic trajectories with small amplitudes. A different method to compute periodic trajectories was introduced by Poincaré investigating the N-body problem: this is the so-called direct method. The latter technique consists in finding a particular periodic trajectory which minimizesthe action (here L is a given Lagrangian and [t0, t1] isthe time interval of reference), and which is a limit of a minimizing sequence (cf. [6]). The problem can be recast in the framework of optimal control theory, interpreting the derivative of t → x(t) as a control function u(.). These two methods justify the use of a variational approach to compute periodic trajectories in optimal control, and, more precisely, a family of periodic trajectories depending on parameters such as the periods. The first-order necessary conditions for optimality, expressed in terms of the Euler–Lagrange equation in the context of the calculus of variations, are provided in optimal control by the maximum principle, which, due to the periodic structure of the problem, might detect a (parameterized) family of extremals. In these circumstances, second-order analysis turns out to be an important tool in detecting the minimizers for the reference problem. Since the nonuniqueness of periodic minimizers does not allow, in general, to invoke standard second-order sufficient conditions, the necessity of refined second-order conditions was discussed in a series of articles (see for instance [10, 22, 24]), yielding important results which were tested in some “academic” examples.

In control engineering, the importance of the study of periodic optimal controls is illustrated by the following problem areas: the optimization of the production of photobioreactors over a one-day prescribed time period (see for instance [14]), and, more recently, the search of periodic optimal controls in locomotion problems (e.g., walking, flying, swimming), where the state variable x decomposes into two variables (x′ , x″), where x′ corresponds to the displacement variable and x″ stands for the shape variable (the latter must often satisfy periodic requirements in locomotion modeling). In the swimming problem, a swimmer displacement is produced by the deformation of the body interacting with the fluid and a periodic “strategy of deformation” is called a stroke. In the case of micro-organisms evolving in a fluid, inertia is negligible with respect to the viscous effects, and the locomotion at this scale can be presented as a sub-Riemannian (SR) problem in which the cost functional to minimize represents the power expanded by the swimmer. A simplified mathematical model of swimmer is the Three linked spheres introduced by [17]. It turns out that the SR geometry associated with this simplified model corresponds to the Heisenberg group case. This problem is equivalent to the Dido problem and the optimal solutions can be easily computed (cf. [5]). In the latter case, the optimal strokes are ellipses and they allow the swimmer to move along a desired direction [1]. An earlier pioneering model of microswimmerwas introduced in the fifties in [23]; this was subsequently investigated using analytical tools coming from control theory in a recent paper [2].

In this paper, we focus on the so-called Purcell three-link swimmer [20]. By using the resistive force theory (see [13]), it was shown that the dynamics of the swimmer can be expressed explicitly in terms of an ordinary differential equation (ODE) in which the speed of deformation can be interpreted as a control function (see, for instance, [11, 12]). As a result, one obtains a drift-less control system which is linear with respect to the control variables, such as x ̇ = u1F1(x) + u2F2(x). Since the detailed expression of functions F i’s is quite involved, deriving the minimizers in an explicit form is not an easy task. In this paper, we employ the expressions of the vector fields F i’s provided by previous work (cf. [2, 11, 12]) and, applying both geometric and numerical methods, we investigate the minimizers of our reference optimal control problem (modeling the Purcell swimmer) having some periodicity requirements.

The paper is organized as follows. Section 2 is a short introduction to some tools and concepts imported from optimal control theory. These are subsequently employed for the study of some optimal control problems related to the mathematical model of the Purcell three-link swimmer, which is described in Section 3. In Section 4, applying a classical SR-geometry approach, we provide an approximation associated with strokes of small amplitudes. This is the so-callednilpotent approximation and we show that it corresponds to the Cartan flat case [8, 21]. It turns out that the associated extremal curves are integrable in the class of elliptic functions. We provide detailed expressions of the extremals to make easier for the reader to understand how to relate the period of the strokes to Jacobi complete integrals. Subsequently, Section 5 is devoted to the numerical analysis of the reference problem. More precisely, we estimate conjugate points for both normal and abnormal extremals, in relation to second-order conditions. (In this context, an open interesting question concerns the concept of focal point in relation with periodic optimal trajectories). Conjugate points are computed numerically using the Hampath code. They are completed by numerical computations using the Bocop code to evaluate strokes with general amplitudes using the system without any approximation and its energy function.

10.2First- and second-order optimality conditions

First- and second-order necessary conditions for optimality (e.g., the Pontryagin maximum principle) play a crucial role in the selection and the characterization of solutions (minimizers) for problems in optimal control. Very general versions of first- and second-order optimality conditions are now available. Here, we restrict attention to optimal control problems with end-point constraints of the form

in which f(., .) : ℝn × ℝm → ℝn and L(., .) : ℝn × ℝm → ℝare the given functions of class ?2, c(., .) : ℝn × ℝn → ℝℓ is a given function of class ?2, and U ⊂ ℝm is a given set.

Take an optimal trajectory/control couple (x̄(.), ū(.)) for (2.1). The Pontryagin maximum principle (see, e.g., [19]) asserts (under appropriate hypotheses) that there exist a vector-valued function p(.) ∈ W1,1([0, T];ℝn), a vector ν ∈ ℝℓ and a constant λ ≥ 0 such that

Take a trajectory/ control couple (x(.), u(.)) satisfying the control system of (2.1). If all the conditions (i)–(iv) of the Pontryagin maximum principle are satisfied for some absolutely continuous function p(.), vector ν ∈ ℝℓ, and λ ≥ 0, then we call (x(.), p(.)) an extremal.

We shall consider the necessary conditions above both in the “normal” and “abnormal” form. “Normal” means that the maximum principle is valid with the Lagrange multiplier λ (associated with the objective function) different from zero (in this case it is not restrictive to take λ = 1/2, by standard normalization). Whereas “abnormal” means that the maximum principle applies with λ = 0.

The pseudo Hamiltonian (also referred to as “unmaximized” Hamiltonian) ℋ : ℝn × ℝn ×ℝm →ℝm is the function

If ū(t) belongs to the interior of U (this holds true whenever we take U = ℝm), condition (iii) above can be rewritten in the form

Consider the particular case of (2.1) in which we impose partial periodic end-point constraints:

in which x = (x′ , x″) ∈ ℝk × ℝn−k for some fixed integer 0 ≤ k < n, and are given points. Then, x″(.) represents the periodic component of the state trajectory x(.). Notice that the transversality condition (iv) involves only the component p″(.) of the adjoint arc p(.) (which is associated with the “periodic component” of a state arc x̄(.), i.e., x̄″(.)),

Second-order sufficient conditions for (local) optimality have been extensively investigated to derive optimal solutions with the property to be (locally) unique. This cannot be the case of pure periodic (i.e., when k = 0 in problem (2.1)) optimal control problems, in which given any periodic trajectory/control pair, any time translation produces a new periodic trajectory/ control pair with the same cost. Therefore, there is a growing interest in studying second order conditions in a framework which comprises periodic optimal control problems, and testing them in examples coming from applications (cf. [22, 24] and [10]).

The optimal control problem (2.1) can be regarded as an SR problem whenever f and L have a particular structure:

where {Fi : ℝn → ℝn | i = 1, . . . , m} is a family smooth vector fields which is bracket generating. (In the representation above, for simplicity, we are also assuming that the vector fields F i’s are orthonormal.)

In this case the integral cost dt represents the ienergy of a reference trajectory/control couple (x(.), u(.)) at a (given) final time T.

The concept of conjugate time (and conjugate point) plays a crucial role in optimality conditions and can be characterized in terms of the degeneracy of the exponential mapping or, equivalently, of the quadratic form associated with the second variation of the endpoint mapping. A further important feature in the analysis of minimizers is represented by the notion of cut locus. We say that a point x̂ is in the cut locus of a reference (left-end) point x0 if we can find two minimizers joining x0 and x̂. It is well known that in the Riemannian geometry every extremal is normal and x(.) is not a minimizer if and only if there exists a cut or a conjugate point along x(.) referred to the left-end point x(0) (see [6] for more details).

10.3The Purcell three-link swimmer

10.3.1Mathematical model

Purcell’s three-link swimmer

The three-link swimmer is modeled by the position of the center of the second stick x = (x, y), the angle θ between the x-axis and the second stick (the orientation of the swimmer). The shape of the swimmer defined by the two relative angles α1 and α2 (Figure 1). We also denote the length of the two external arms and central links, respectively by L and L2. In what follows, x′ (resp. x″) corresponds to (x, y) (resp. to (θ, α1, α2)).

Dynamics via resistive force theory

We approximate the non local hydrodynamic forces exerted by the fluid on the swimmerwith local drag forces depending linearly on the velocity. For each i ∈ {1, 2, 3}, wedenote by and the unit vectors parallel and perpendicular to the i-th ⊥link, andwe also introduce υi(s) the velocity of the point at distance s from the extremity of the i-th link, that is

The force f i acting on the i-th segment is taken as

where ξ and η are, respectively, the drag ⊥coefficients in the directions of and

Neglecting inertia forces, Newton laws are written as

where F is the total force exerted on the swimmer by the fluid and ez = ex ∧ ey,

and Tx is the corresponding total torque computed with respect to the central pointx,

where xi = (xi , yi), for i = 1, 2, 3, corresponds to the left-end point of the i-th link,and xi(s) = xi + sei.

Since the f i(s) are linear in ẋ, θ̇, α̇1, α̇2, the system (10.3.1) can be rewritten as

where z(t) := (α1, α2, x, y, θ)(t)T. The matrix A(z) is known as the “grand resistance matrix” and is invertible (see [2]). Then the dynamics of the swimmer is finally expressed as an ODE system

ż(t) = f(z, α̇1, α̇2) = α̇1(t) F1(z(t)) + α̇2(t) F2(z(t)) ,

where 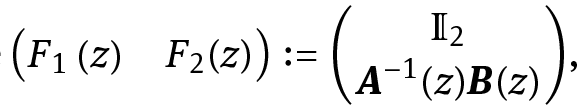with ?2 the 2×2 identity matrix. The detailedexpression for the F i is quite complicated and takes several pages (see, e.g., [2, 11, 12]).

At the end, the dynamics of the swimmer is governed by an ODE linear with respectto the speed of deformation, α̇ i, i = 1, 2. By considering the latter as a control function, ui := α̇ i, i = 1, 2, we then obtain a linear control problem without a drift.

By definition, the power expanded during a time interval [0, T] by the swimmer is given by (see [1] for more details)

Notice that the power is then a quadratic function with respect to the speed of deformation of the body.

10.4Local analysis for the three-link Purcell swimmer

The SR structure of the Purcell swimmer model allows us to consider a motion of first-order approximation which takes into account the nonisotropic behavior of the SR distance, called nilpotent approximation. This approximation is called nilpotent in the sense that the vector fields F1 and F 2 can be approximated (using new coordinates, called privileged coordinates) by vector fields F1̂ and F2̂ which generate a nilpotent Lie algebra. The nilpotent approximation together with the accompanying privileged coordinates constitutes the basis for the infinitesimal calculus adapted to the particular structure of the (non honolomic) control system modeling the Purcell swimmer. We refer the reader for these constructs for instance to [3].

10.4.1Computations of the nilpotent approximation

Let us denote D = span{F1̂ , F2̂ }, D1 = D, D2 = span{D1 ∪ [D1, D2]}, and D3 = span{D2 ∪ [D1, D2]}. At the point x0, we have a (2, 3, 5) distribution correspondingto the respective ranks of D1, D2, andD3.

We write the control system as

Feedback group

The pseudo-group ? = (φ, β) is defined by the actions:

–local diffeomorphism φ:

let ẋ = X(x) and x = φ(y).

The action of φ on a vector field X is (φ ∗ F1, φ ∗ F2).

–feedback β:

u = β(x)υ where β is a 2 × 2 invertible matrix. The action of β transforms F into Fβ.

Computations

Let us define the variables xi, for i = 1, . . . ,5, as x1 = α1, x2 = α2, (x3, x4) = x, x5 = θ. In the rest of the computations, we set L = 1, L2 = 2, ξ = 1, η = 2. Hence, the 2-jets of F1 and F 2 at zero are expressed by

The normal forms fo these mappings (see [21]) are

We introduce the weights 1 for x1, x2, 2 for x3, and 3 for x4, x5. If xi is of order p, is of order −p to define the nilpotent normal form of order −1.

We write φ = φN o . . ., o φ1 : ℝ5 → ℝ5. We shall employ N = 13 steps. At each step i, for i = 1, . . . , N, of the computations, we shall use the following notation:

–x = (x1, x2, x3, x4, x5) are the old local coordinates and y = (y1, y2, y3, y4, y5) the new ones resulting from the change of variables φi,

–xj = (yj) : ℝ → ℝ denoting the jth component of φifor some j ∈ {1, . . . ,5}.The other components are the identity transformations.

The successive change of variables is given by

Neglecting terms of order greater than 3, we denote by F1̂ , F2̂ the resulting vectorfields.

Remark 4.1. The construction of the diffeomorphism relates the normalized coordinates to the physical coordinates. A similar transformation details the effect on a frame.

10.4.2Integration of extremal trajectories

For two vector fields F and G, we use the following Lie bracket convention:

Computing we have

All brackets of length greater than 3 are zero.

We introduce the Hamiltonian lifts related to the vector fields above:

H1 = ⟨p, F1̂ (x)⟩ = p1,

H3 = ⟨p, [F1̂ , F2̂ ](x)⟩ = −p3 − 2x1p5,

H4 = ⟨p, [[F1̂ , F2̂ ], F1̂ ](x)⟩ = −2p5 ,

H5 = ⟨p, [[F1̂ , F2̂ ], F2̂ ](x)⟩ = p4 .

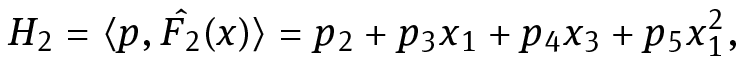
We recall the following relation for the Poisson brackets of two lifting Hamiltonians HF and HG of vector fields F and G. If

HF = ⟨p, F(x)⟩, HG = ⟨p, G(x)⟩ ,

are the Hamiltonian lifts of vector fields of F and G, then we have

{HF , HG} = ⟨p, [F, G](x)⟩ .

We consider the SR Cartan flat case [8, 21]

Normal case

The pseudo-Hamiltonian is

The Pontryagin maximum principle [19] gives ui = Hi.

Hence, the true Hamiltonian is

Computing we have

Ḣ 1 = dH1(H) = {H1, H2}H2 = ⟨p, [F1̂ , F2̂ ](x)⟩H2 = H2H3 ,

Ḣ 2 = −H3H1,

Ḣ 3 = H1H4 + H2H5 ,

Ḣ 4 = 0 hence H4 = c4,

Ḣ 5 = 0 hence H5 = c5 .

Fixing the level energy, we set H1 = cos(θ) and H2 = sin(θ).

Ḣ 1 = − sin(θ)θ̇ = H2H3 = sin(θ)H3 .

Hence, θ̇ = −H3 and

θ̈ = −(H1c4 + H2c5) = −c4 cos(θ) − c5 sin(θ) = −A sin(θ + ϕ)

where A and ϕ are constants (depending only on c4 and c5).

By identification, we get A sin(ϕ) = c4 and A cos(ϕ) = c5.

Let ψ = θ + ϕ, we get

where B is a constant.

We have the following two cases:

Oscillating case

We introduce ω2 = A and with 0 < k < 1, and we obtain [16]

sin(ψ/2) = k sn(u, k), cos(ψ/2) = dn(u, k)

where u = ωt + φ0.

H1 and H 2 are the elliptic functions of the first kind. Therefore, the system becomes

Parameterizing (4.4) with respect to u, we have

Proposition 4.2. The solution x(u) of the system (4.4) can be expressed as a polynomial function of (u, sn(u), cn(u), dn(u), E(u)).

Proof. Integrating equations (4.5)–(4.9) and using formulae (4.10), we obtain the result.

Remark 4.3 ([16]). – sn, cnare4K-periodics,

–dnis2K-periodic,

– where E , K are complete integrals and Z is the 2K-periodic zetafunction.

The next step is to compute the x variables using quadratures in the oscillating case. Since x(0) = 0, solutions depend upon four independent parameters provided by Hi(0)’s for i = 1, . . . ,5, and the relation H1(x(0), p(0))2 + H2(x(0), p(0))2 = 1.

To integrate equations (4.5)–(4.9) explicitly, we use the following primitive functions (see [16])

The final expressions of the solution (xi(u))i=1,...,5 of (4.4) (we supply a MAPLE code to check the correctness of the expressions):

Rotating case

We can perform the same computations as in the oscillating case.

Abnormal case

According to [7], we consider the minimal time problem for the single-input affine system

ẋ(t) = F1̂ (x(t)) + u(t)F2̂ (x(t)) ,

where u is a scalar control.

Denoting x(.) a reference minimum time trajectory, since we consider abnormal extremals, it follows from the Pontryagin maximum principle that along the extremal lift of x(.), there must hold H 2(x(.), p(.))=0 and derivating with respect to t,

{H1, H2}(x(.), p(.)) = 0 must hold too. Thanks to a further derivation, the extremals associated with the controls

satisfy the constraints H 2 = {H1, H 2} = 0 along (x(.), p(.)) and are solutions of

where Ha is the true Hamiltonian

From the transversality conditions of the Pontryagin maximumprinciple, the constraint H1(x(.), p(.)) = 0 must hold too. The extremal system subject to the constraints H1 = H2 = {H1, H 2} = 0 is integrable and solutions can be written as

with (x1(0), x2(0), x3(0), x4(0), x5(0), p1(0), p2(0), p3(0), p4(0), p5(0)) are constants satisfying

p1(0) = 0, p2(0) = p5(0)x1(0)2 − p4(0)x3(0), p3(0) = −2p5(0)x1(0) .

10.5Numerical results

This section presents the numerical simulations performed on the Purcell swimmer problem. Simulations are obtained by applying both direct and indirect methods, and using the solvers Bocop and HamPath. We use the multipliers from the solutions of the direct method to initialize the costate variables in the indirect approach. We show the optimal trajectories obtained for the nilpotent approximation and the true mechanical system.

Bocop

Bocop (www.bocop.org, [4]) implements a so-called direct transcription method. Namely, a time discretization is used to rewrite the optimal control problem as a finite-dimensional optimization problem (i.e nonlinear programming), solved by an interior point method (Ipopt).We recall the optimal control problem, formulated with the state q = (α1, α2, x, y, θ) and control u = (α̇1, α̇2)

HAMPATH

The HAMPATH software (www.hampath.org, [9]) is based upon indirect methods to solve optimal control problems using simple shooting methods and testing the local optimality of the solutions.

More precisely, two purposes are achieved with HAMPATH:

–Shooting equations: to compute periodic trajectories of the Purcell swimmer, we consider the true Hamiltonian H given by the Pontryagin maximumprinciple and the transversality conditions associated with. The normal and regular minimizing curves are the projection of extremals solutions of the boundary two values problem

where q = (x, y, α1, α2, θ), p = (px , py , pα1 , pα2 , pθ) and T > 0 is fixed.

Due to the sensitivity of the initialization of the shooting algorithm, the latter is initialized with direct methods namely the Bocop toolbox.

–Local optimality: to show that the normal stroke is optimal, we perform a rank test on the subspaces spanned by solutions of the variational equation with suitable initial conditions [7].

10.5.1Nilpotent approximation

Notation: state x = (x1, x2, x3, x4, x5), costate p = (p1, p2, p3, p4, p5), F1̂ , F2̂ the normal form is given by (4.1), and H1 and H 2 are the respective Hamiltonian lifts.

Normal case

In the normal case, we consider the extremal system given by the true Hamiltonian given by (4.2).We compute the optimal trajectories with Hampath, and show the state and adjoint variables as functions of time in Figure 2.We also illustrate the conjugate points computed according to the algorithm in [6], as well as the smallest singular value for the rank test.

Property on the first conjugate point. Let us consider the fixed energy level

H1(x(0), p(0))2 + H2(x(0), p(0))2 =1 along the extremals and the initial state x(0) = 0. We take a large number of random initial adjoint vectors p(0) and numerically integrate the extremal system. For each normal extremal, we compute the first conjugate time t1c, the pulsation ω = (p4(0)2 + 4 p5(0)2)1/4, and the complete elliptic integral K(k), where k is the amplitude

Let γ(.) be a normal extremal starting at t = 0 from the origin and defined on [0,+∞[. As illustrated in Figure 3, there exist a first conjugate point along γ corresponding to a conjugate time t1c satisfying the inequality

Remark 5.1. In Section 10.4.2 u = ωt + φ0 is the normalized parametrization of the solutions.

Abnormal case

Figure 4 illustrates the time evolution of the state variables. We check the second-order optimality conditions thanks to the algorithm given in [7]. Both the determinant test and smallest singular value for the rank condition indicate that there is no conjugate time for abnormal extremals (Figure 5).

10.5.2True mechanical system

We now consider the optimal control problem (5.1) consisting in minimizing either the mechanical energy (3.1) or the criterion |u|2.

Direct method. In the first set of simulations performed by Bocop, we set T = 10,xf = 0.5, and the bounds a = 3 large enough so that the solution is actually unconstrained. The state and control variables for the optimal trajectory are shown in Figures 6–8, and we observe that the trajectory is actually a sequence of identical strokes. Figure 9 shows the phase portrait for the shape angles α1, α2, which is an ellipse. The constant energy level satisfied by the optimal trajectory means that the phase portrait of the controls is a circle for the |u|2 criterion, but not for the energy criterion. The

adjoint variables (or more accurately in this case, the multipliers associated with the discretized dynamics) are shown in Figures 10–11.

Indirect method. Now, we use the multipliers from the Bocop solutions to initialize the shooting algorithm of HamPath. Figures 12 and 13 and Figures 14 and 15 represent, respectively, an nonintersecting curve and an eight-shape curve with the same boundary values. Figures 16 and 17 show another eight shape curve obtained for different boundary values. In these three cases, we check the second-order optimality conditions according to [6] and observe that there is no conjugate point on [0, T], where T = 2π.

10.5.3The Purcell swimmer in a round swimming pool

Clearly, due to the symmetry with respect to the initial orientation of the body, we havethe following result.

Lemma 5.2. If α(t), θ(t), is an extremal solution associated to u(.) with θ(0) =0, then

x(t) = cos(θ0)x(t) − sin(θ0)y(t) ,

y(t) = sin(θ0)x(t) + cos(θ0)y(t)

is the solution associated with u(.) with θ(0) = θ0, (x(0), y(0)) = (x0, y0) and with the same cost (|u|2 criterion or energy case).

Remark 5.3. This leads to define a one-parameter family of isocost extremals starting from any point. Practically, this justifies the following numerical computation.

Minimizers having the circle as a right-end point constraint.

We present now simulations of the following boundary value problem:

where H(q, p) is the true Hamiltonian for the |u|2 criterion, q = (x, y, α1, α2, θ), p = (px , py , pα1 , pα2 , pθ), and T > 0 is fixed.

For numerical simulations we set T = 2π and R = 0.1. Figures 18 and 19 show an optimal trajectory, with the test rank for the second-order optimality conditions indicating that there is no conjugate time. Figure 20 represents the projection in the plane (x, y) of two trajectories for different initial conditions, with the end-point circle constraint drawn in black line.

It turns out that this problem has a particular symmetry, which, taking the initial position angle θ0 as a parameter, allows us to embed minimizers in a (one-parameter) family of minimizers. As a particular consequence, we obtain the nonuniqueness of minimizers.

10.6Conclusions and future work

In the present paper, we focus on some aspects related to first- and second-order optimality conditions applied to a mathematical model of the Purcell three-link swimmer. Combining numerical methods with a geometrical approach, we investigate crucial features of this model, as its nilpotent approximation, the integrability of extremals, the periodicity of minimizers, providing and estimate of conjugate points for bothnormal and abnormal extremals. This model exhibits particular properties (such as symmetries) which make it a very good case study to investigate further (nontrivial) features concerning second-order optimality conditions, when nonunique minimizers occur.

Acknowledgment: Work supported in part by the French Space Agency CNES, R&T action R-S13/BS-005-012 and by the region Provence–Alpes–Côte d’Azur. Laetitia Giraldi was funded by the labex LMH through the grant ANR-11-LABX-0056-LMH in the “Programme des Investissements d’Avenir”.