9.3Proof of Theorem 2.1

We first observe that without loss of generality we may assume that the function c F(.) in (H2) is actually essentially bounded, also when we consider the case represented by condition (CQ b), replacing cF(.) with a constant c ≥ 1. This is standard reduction procedure based on a change of time variables (cf. [11]):

We state two lemmas, which have a key role in the proof of the nondegeneracy respectively in case (CQ a) and in case (CQ b) of Theorem 2.1.

Lemma 3.1 (Case where x̄(S) ∈ A0). Consider a (nonempty) closed set A ⊂ ℝn and a multifunction F : [S, T]×ℝn ⇝ℝn such that for some constants δ > 0, c ≥ 1, α > 0 and τ ∈ (0, T − S], for a function kF(.) ∈ L1([S, T], ℝ+), and for a given F-trajectory x̄(.), the assumptions (H2) and (CQa) of Theorem 2.1 are satisfied. Then, there exist constants ρ ∈ (0, δ), τ′ ∈ (0, τ] and K > 0 such that: given any F-trajectory x̂(.) on [S, T] and ε ≥ 0 satisfying

we can find an F-trajectory x(.) on [S, T] such that:

Lemma 3.1 represents a local version of known linear W1,1-estimates obtained for control systems with smooth state constraints (cf. [3]).

Lemma 3.2 (Case where x̄(S) ∈ A A0). Consider a (nonempty) closed set A ⊂ ℝn and a multifunction F : [S, T] ×ℝn ⇝ ℝn such that for some constants δ > 0, c ≥ 1, for a function kF(.) ∈ L1([S, T], ℝ+), and for a given F-trajectory x̄(.), the assumption (H2) of Theorem 2.1 is satisfied. Then, for any vector ῡ̄ ∈ int TA(x̄(S)), there exist constants ε̄ > 0, θ > 0, ρ ∈ (0, δ), τ ∈ (0, T − S] and K > 0 such that: given any F-trajectory x̂(.) on [S, T] and ε ∈ [0, ε̄] satisfying

and for any ẑ ∈ πA(x̂(S)), we can find an F-trajectory x(.) on [S, T] such that:

The proof of Lemma 3.2 will be provided in Section 9.4.

We shall continue the proof of Theorem 2.1 assuming that hypotheses (H1)–(H3) and (CQ b) are satisfied. For the case in which hypothesis (CQ a) is assumed [instead of (CQ b)], the theorem can be proved applying a similar technique (invoking Lemma 3.1 instead of Lemma 3.2), cf. also the proof of [22, Theorem 2.1].

The proof approach is along similar lines to that of [22]. Nevertheless, since the nature of the state constraints (and in turn the related distance estimates provided by Lemma 3.2) differs from that of [22], the analysis employed herein requires some ideas that are new with respect to the earlier work.

To begin with, assumption (CQ b) of Theorem 2.1 guarantees the existence of a vector ῡ̄ ∈ int TA(x̄(S)), which means that all the assumptions of Lemma 3.2 are satisfied.

Consider the constants ε̄ > 0, θ > 0, ρ ∈ (0, δ), τ ∈ (0, T − S], and K > 0 provided by Lemma 3.2. We can always suppose also that τ ≤ τ0 and ρ ≤ ρ0 [where τ0 and ρ0 are the constant given by condition (CQ b)]. Take any arbitrary sequence εi ↓ 0 with εi ≤ ε̄ and, for each i ∈ ℕ, set the function ϕi : ℝn × ℝn × ℝ+ → ℝ:

ϕi(y0, y1, d) := maxi2{g(y0, y1) − g( x̄ (S), x̄ (T)) + , d, dE0∩A(y0), dE1 (y1)} .

Define also the sets of functions

X := {y(.) ∈ W1,1([S, T], ℝn ) : ẏ(t) ∈ F(t, y(t)) a.e. and

‖y(.) − x̄(.)‖W1,1(S,T) ≤ ρ} ,

Consider now the space X with the metric induced by the W1,1-norm. Then, X turns out to be complete. Notice also that (w.r.t. the topology induced by the W1,1-norm) the set X1 is closed. Moreover, the function Φi : X →ℝ

is continuous on X, and so it is continuous also on X1. Since x̄ (.) ∈ X1 is an minimizer for Φi on X 1, for each i ∈ ℕ, Ekeland’s Theorem (cf. [24, Theorem 3.3.1]) guarantees the existence of an arc xi(.) ∈ X1 such that

and such that the functional

attains a (unique) minimum at xi(.). As a consequence, by eventually a subsequence extraction, we obtain that

By extracting subsequences (without relabeling) we can arrange that either of the following situations arises:

(a)xi(.) ≠ x̄(.), for all i = 1, 2, 3, . . . or

(b)xi(.) ≡ x̄(.), for all i = 1, 2, 3, . . . .

Notice also that the functional Ji(.) is, in fact, uniformly Lipschitz continuous on X with respect to the W1,1-norm. Let KJ > 0 be a constant independent of i such that

Associated with any minimizer xi(.) for Ji(.), we define the positive number

The following lemma is an easy consequence of the Max-rule for subdifferentials, and the fact that either xi(.) ≠ x̄(.) or xi(.) ≡ x̄(.) for all i = 1, 2, 3, . . . . Observe that, in the first case, owing to assumption (CQ b), since each xi(.) ∈ X1, we have that dE0∩A(xi(S)) < dE1 (xi(T)).

Lemma 3.3. Take any subgradient

where xi(.)’s are the minimizers for Ji(.) and di’s are the corresponding numbers defined in (3.5). Then for all i large enough, we obtain either

(a)(case xi(.) ≠ x̄(.))

for some a ≥ 0 and ξ1 ∈ NE1 (e1), in which e1 ∈ πE1 (xi(T)) and

or

(b)(xi(.) ≡ x̄(.))

Lemma 3.4. Assume that the hypotheses of Lemma 3.2 hold true. Then there exists i0 ∈ ℕ such that, for all i ≥ i0, xi(.) is a W1,1-local minimizer for the problem

Proof. The proof of this lemma is based on a standard penalization argument, which is applicable owing to Lemma 3.2. Wewrite the proof here in detail to highlight the role of the W1,1-linear estimate provided by Lemma 3.2. Since εi ↓ 0 with εi ≤ ε̄, there exists i0 ∈ ℕsuch that we also have for all i ≥ i0. Suppose, for contradiction, that the statement is false. Recall that ῡ̄ ∈ int TA(x̄(S)) is given by assumption (CQ b). It follows that we can choose such that for all j ∈ ℕ, j ≥ i0, there exist i ≥ j and ŷ(.) ∈ X such that

and

Write Observe that and the fact that thexi(.)s belong to X1, guarantees that ε ≤ δ′ ≤ ε̄. Then, owing to Lemma 3.2 (applied for the F-trajectory ŷ(.) and for the violation of the state constraint on [S, S + τ]), there exist θ > 0 and an F-trajectory y(.) on [S, T] such that

Bearing in mind that also

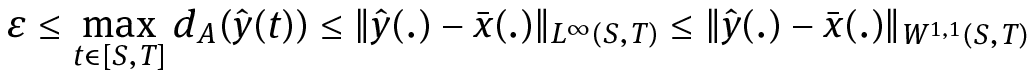
(for x̄(.) is feasible), it follows that

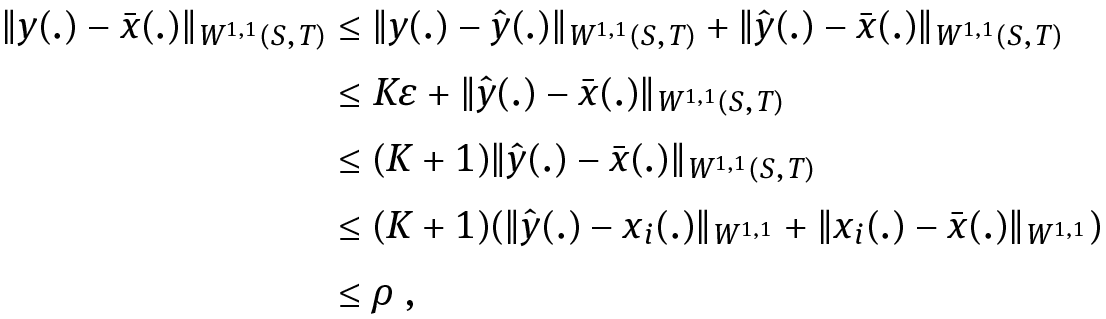
and therefore y(.) ∈ X1. Moreover, we would have

which contradicts the minimality of xi(.) on X1.

A consequence of Lemma 3.4 is that, for i ∈ ℕ with i ≥ i0, the state trajectory

is a W1,1-local minimizer for the state-constrained optimal control problem

in which the (final) cost is

the velocity set is represented by the multivalued function

and the function h̃ : [S, T] × ℝn × ℝ× ℝ × ℝ → ℝ (which provides the state constraint by means of a functional inequality) is defined by:

Assume now that we are in case (a): xi(.) ≠ x̄(.), for all i.

Notice that the necessary conditions for the optimality referred to problem (3.7) [24, Theorem 10.3.1] are applicable, and, consequently, for each i, we obtain a constant λ̃i ≥ 0, a function p̃i(.) = (pi(.), χi(.), ζi(.), ψi(.)) ∈ W1,1([S, T];ℝn+3), which is the costate trajectory associated with the state x̃i(.), a Borel measurable function μi(.) on [S, T] and a μi-integrable function γ̃i : [S, T] → ℝn+3, such that

in which q̃i(.) : [S, T] → ℝn+3 is the function

supp μi denotes the support of the measure μi, and is the set

h̃(t, x̃) := co { ζ : there exist x̃j → x̃, tj → t and ζj → ζ s. t.

We observe that the Euler–Lagrange inclusion (ii)′, the transversality condition (iii)′ and condition (v)′, bearing in mind the information provided by Lemma 3.3, imply that there exist (for i large enough) such that (vi)′ , and , (vii)′ , where

and

Since the multivalued map G is kF(.)-Lipschitz w.r.t. the state variable around the G-trajectory x̃(.) (recall that, around the reference F-trajectory x̄(.), kF(.) is the function as defined in Theorem 2.1), we notice that (ii)′ implies also that

Notice that the necessary conditions apply in the normal form. Indeed, assume that λ̃i = 0, then from (3.8)–(3.11), we would obtain

which, combined with (3.13), would imply p̃i ≡ 0 (using Gronwall’s Lemma). But this contradicts (i)′.

The above relations are valid for arbitrary i ∈ ℕ sufficiently large. Standard convergence analysis (cf. [22] or [24]), following the extraction of subsequences, providesthat for some constants λ̃ ≥ 0 and a, b, β0, β1 ∈[0, 1], → ξ1 ∈ ℝn for some vector ξ1 ∈ ℝn ∩ ?. Furthermore, pi(.) → p(.) uniformly, pi(.) → ṗ(.) weakly in L1, μi(.) → μ(.) and γi(.)μi(.) → γ̄(.)μ(.) in the appropriate weak-* topology (where γi(.), having its values in ℝn, is relative to the adjointarc pi(.) and it represents the first component of γ̃i(.)) and qi(.) → q(.) a.e., for someabsolutely continuous function p(.), function of bounded variation q(.), Borel measure μ(.) and μ-integrable function γ̄(.). The limit of the relationships (i)′, (iv)′-(vii)′,(3.8)–(3.12) yield

in which q(.) : [S, T] → ℝn is the function

where γ(.) := (γ̄(.))p, that is the first n-components of the μ-integrable function γ(.), corresponding to the p-variable. The state constraint in the optimal control problem (3.7) is formulated as a functional inequality constraint by means of the function h̃ ,which in turn involves the distance function to the set A, dA(.). This translates into necessary optimality conditions for our reference problem (P), in which we assume implicit state constraints (i.e., the state constraint set is a general closed set). The simple analysis, involved in deriving the necessary conditions for the implicit constraints from the necessary conditions for the functional inequality constraints, is described in [24] (see Remark (e) p. 332, and Remark (b) p. 370). This allows us to obtain property (i) of Theorem 2.1.

Observe that using the same argument as for the multipliers λ̃i, we conclude that λ̃ ≠ 0. Define λ := aλ̃. Then, λ, p(.), ν(.) := ∫[S,.] γ(s) dμ(s) satisfy assertions (ii)–(iv) of the theorem statement.

It remains to prove the nondegeneracy condition (assertion (v) in the statement of Theorem 2.1):

Assume to the contrary that (3.14) is violated. Then λ = 0 (which, since λ̃ ≠ 0, implies a = 0), |p(S) + ν({S})| = 0 and ∫(S,T] dμ(s) = 0, that together with the first condition of (v)″ gives b = 0. As a consequence, from the first equality in (vi)″ we obtain that |ξ1| = 1, and therefore, owing to (iii)″,

Conversely, invoking Gronwall’s inequality, conditions ∫(S,T]dμ(s) and |p(S) + ν({S})| above yield:

The two relations (3.15) and (3.16) provide a contradiction. Thus, we have proved also the nondegeneracy condition (3.14).

Assume finally that we are in case (b): xi(.) ≡ x̄(.), for all i.

Necessary optimality conditions for problem (3.7) still apply, providing the same conditions (i)″–(v)″ and (vii)″ above, whereas (vi)″ is replaced by:

(vi)″a = 1, and β0 + β1 = 1 .

This immediately implies that the Lagrange multiplier associated with the cost function λ = λ̃ > 0, and therefore, in this case the necessary conditions are nondegenerate (in fact they apply in the normal form), and this concludes the proof of Theorem 2.1.

9.4Proof of Lemma 3.2

Fix any ῡ̄ ∈ int TA(x̄(S)). Invoking the characterization of the interior of the Clarketangent cone, we can find such that

Define and such that Define also Consider any F-trajectory x̂(.) and any ε ∈ [0, ε̄] for whichcondition (3.2) is valid.

Fix now by ẑ0 any element in πA(x̂(S)). Condition (3.2) clearly ensures that |ẑ0 − x̂(S)| ≤ ε . Invoking the Filippov Existence Theorem (cf. [2] or [24]) to the reference trajectory x̂(.), we obtain an F-trajectory ẑ(.) on [S, T] such that:

Notice that:

Write Notice that since Define the arc z(.) as follows:

z(t) := θ0εˊῡ + ẑ(t), ∀t ∈ [S, T] .

Since dA(ẑ(t)) ≤ ε′, for all t ∈ [S, S + τ], we have

Take any y ∈ πA(ẑ(t)), then we can easily establish the following estimate for all t ∈ (S, S + τ]:

It follows that from the choice of δ0, ρ and τ, we have ∀t ∈ [S, S + τ]:

Consequently, (4.1), (4.2) and (4.3) ensure that

We apply once again the Filippov Existence Theorem considering ẑ(.) as a reference arc and z(S) = ẑ(S) + θ0ε′ῡ̄ as the new initial state point [recall that ẑ(S) = ẑ0 ∈ πA(x̂(S))]: we obtain an F-trajectory x(.) such that x(S) = z(S) and for all t ∈ (S, T]:

Therefore, since x(S) = z(S) and ż (t) = z(t) a.e., we have

Then, from the choice of τ,

We deduce from the relations (4.4) and (4.6) above that x(t) ∈ z(t) + ε′? ⊂ A, ∀t ∈ [S, S + τ] . Furthermore, invoking again (4.5), we have:

Finally, notice that:

The validity of (3.3) follows taking the constant in the expressionof x(S) and for the desired linear W1,1-estimate.

9.5Example

We provide an example to illustrate the result provided by Theorem 2.1, when the left end-point of the minimizer belongs to a region in which the state constraint is non-smooth. The example illustrates the relevance of the constraint qualification (CQ b): this implies the nondegeneracy of the necessary optimality conditions even if a (convexified) inward pointing condition (for the velocity set) is not necessarily satisfied. In this example we have a discontinuous time-dependent velocity set.

Example. We consider the optimal control problem with state constraints:

where

in which for k = 0, 1, 2, 3, . . .

Consider the arc z(.) : [0, 1] → ℝ defined as: z(0) = 0, z(tk ) := (−1)k tk, and ż(t) = (−1)k2 for t ∈ (tk+1, tk], Then, the F-trajectory

x̄(t) := (t, z(t), 0), ∀t ∈ [0, 1] ,

is a W1,1 minimizer for problem (P1), for x̄(0) = (0, 0, 0) ∈ E0, x̄(1) = (1, 1, 0) ∈ E1 and x̄3(1) = 0.We claim that condition (CQb) is satisfied. Indeed, clearly int TA(x̄(0)) ≠ 0. Fix now any τ0 ∈ (0, 1) and ρ0 > 0. Consider the family of F-trajectories

X1 := {x(.) ∈ W1,1([0, 1], ℝ3) : ẋ(t) ∈ F(t) a.e. ,

‖x(.) − x̄(.)‖W1,1(0,1) ≤ ρ0 and x(t) ∈ A ∀ t ∈ [0, τ0]} .

Observe that for all y(.) ∈ X1 such that y(.) ≠ x̄(.), we necessarily have y(0) = (y1(0), y2(0), y3(0)) ∈ A and, so, y1(0) > 0.

Moreover, if y3(1) = 0, then it follows that y(1) = y(0) + x̄(1), and we immediately have

dE0∩A(y(0)) = |y2(0)| < |y(0)| = dE1 (y(1)) .

If y3(1) > 0, then we obtain

We have proved the claim.

Therefore, the necessary conditions apply in the nondegenerate form (in the senseof (v) of Theorem 2.1).

Conversely, if we had a different choice for the left end-point condition in problem (P1), for instance E0 = {(0, 0, 0)} (observe that in this case (CQ b) is not verified), then the necessary conditions for optimality would be compatible with the degeneracy condition

Indeed, it is easy to verify that the necessary conditions of optimality to the reference minimizer x̄(.), would be applicable in a degenerate form provided that (p(.) ≡ const)

and

Notice that (5.2) is just the left end-point transversality condition, whereas (5.3) follows immediately from the degenerate condition (5.1) and from the fact that ν({0}) ∈ N A(x̄(0)). As a consequence, the (standard) necessary conditions apply (in the degenerate form) not only for the minimizer x̄(.) but also for any feasible F-trajectory x(.) having x(0) = (0, 0, 0) as left end-point. This is possible with the trivial choice of multipliers λ = 0, γ = ξ, μ = δ{0}, p(.) = −ξ, in which ξ ∈ NA((0, 0, 0)) ∩ (? {0}) and δ{0} is the unit measure concentrated at {0}.

Bibliography

[1]A. V. Arutyunov and S. M. Aseev, Investigation of the degeneracy phenomenon of the maximum principle for optimal control problems with state constraints, SIAM J. Control Optim., 35:930–952, 1997.

[2]J. P. Aubin and H. Frankowska, Set-valued Analysis. Birkhäuser, Boston, 1990.

[3]P. Bettiol, A. Bressan, and R. B. Vinter, On trajectories satisfying a state constraint: W1,1 estimates and counter-examples. SIAM J. Control Optim., 48:4664–4679, 2010.

[4] P. Bettiol and G. Facchi, Linear estimates for trajectories of state-constrained differential inclusions and normality conditions in optimal control, J. Math. Anal. Appl., 414:914–933, 2014.

[5]P. Bettiol and H. Frankowska, Normality of the maximum principle for non convex constrained Bolza problems, J. of Differential Equations, 243 (2007), no 2, 256–269.

[6]P. Bettiol, H. Frankowska, and R. B. Vinter, L∞ estimates on trajectories confined to a closed subset, J. of Differential Equations, 252:1912–1933, 2012.

[7]P. Bettiol, N. Khalil, and R. B. Vinter, Normality of generalized Euler–Lagrange conditions for state constrained optimal control problems, J. Convex Anal., 23(1):291–311, 2016.

[8]P. Bettiol and R. B. Vinter, Trajectories Satisfying a Smooth State Constraint: Improved Estimates, IEEE TAC, 56(5):1090–1096, 2011.

[9]A. Bressan and G. Facchi, Trajectories of differential inclusions with state constraints. J. Differential Equations, 250:2267–2281, 2011.

[10]F. H. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, New York, 1983.

[11]F. H. Clarke, Necessary Conditions in Dynamic Optimization, Memoirs of the American Mathematical Society, no. 173, 2005.

[12]A. Yu. Dubovitskii, A. A. Milyutin, Extremum problems with constraints, Soviet Math., 4:452– 455, 1963.

[13]A. Yu. Dubovitskii, A. A. Milyutin, Extremum problems in the presence of restrictions, U.S.S.R. Comput. Math. Math. Phys., 5(3):1–80, 1965.

[14]M. M. A. Ferreira, F. A. C. C. Fontes, and R. Vinter, Nondegenerate necessary conditions for non-convex optimal control problems with state constraints, J. Math. Anal. Appl., 233(1):116–129,1999.

[15]M. M. A. Ferreira and R. Vinter, When is the maximum principle for state constrained problems nondegenerate?, J. Math. Anal. Appl., 187(2):438–467, 1994.

[16]F. A. C. C. Fontes, S. O. Lopes, and R. de Pinho, On constraint qualifications for nondegenerate neccesary conditions of optimality applied to optimal control problems, Discrete Contin. Dyn. Syst., 29(2):559–575, 2011.

[17]F. A. C. C. Fontes and S. O. Lopes, Normal forms of necessary conditions for dynamic optimization problems with pathwise inequality constraints, J. Math. Anal. Appl., 399(1):27–37, 2013.

[18]H. Frankowska, Normality of the maximum principle for absolutely continuous solutions to Bolza problems under state constraints. Control Cybernet., 38(4B) (2009), 1327–1340.

[19]H. Frankowska and D. Tonon, Inward Pointing Trajectories, Normality of the maximum principle and the non occurrence of the Lavrentieff phenomenon in optimal control under StateConstraints, J. Convex Anal., 20(4):1147–1180, 2013.

[20]M. Palladino and R. B. Vinter, Regularity of the Hamiltonian along Optimal Trajectories, SIAM J. Control Optim., 53:1892–1919, 2015.

[21]F. Rampazzo and R. B. Vinter, A theorem on existence of neighboring trajectories satisfying a state constraint, with applications to optimal control. IMA J. Math. Control Inform., 16:335–351, 1999.

[22]F. Rampazzo and R. B. Vinter, Degenerate optimal control problems with state constraints. SIAM J. Control Optim., 39:989–1007, 2000.

[23]R. T. Rockafellar, Clarke’s tangent cones and the boundaries of closed sets in ℝn, Nonlinear Anal., 3(1):145–154, 1979.

[24]R. B. Vinter, Optimal Control, Birkhäuser, Boston, 2000.