Besides, the torsion is
with τ̄Quad =
Proof. We carry out the same computation as in the proof of Lemma 10.3, now up to the order 2 in the r̃j’s. The truncated expression is a trigonometric polynomial in the angles φ̃ j of degree ≤ 4. Eliminating nonresonant monomials, that is, functions of k ⋅ φ with k ⋅ αQuad(0), is a classical matter. Two kinds of terms cannot be eliminated by averaging:
Such monomials actually cannot occur in the expansion, due to the invariance by rotations (theywould not satisfy the d’Alembert relation [24, 64]).33Adirect computation leads to the given expression of the torsion τQuad.
Note that the torsion τQuad, as a function of Λ1 and Λ2, extends analytically outside ℒ(2) (as often do first-order normal forms). This allows us to define the quadrupolar frequency map
a first-order approximation of the normal frequencies.
Proposition 10.6. The first quadrupolar frequency map has constant rank 3 and, in restriction to the symplectic submanifold obtained by fixing vertically the direction of the angular momentum, is a local diffeomorphism.
Proof. For this lemma, we denote by C = (Cx , Cy , Cz) ∈ ℝ3 the angular momentum of the first two planets. The submanifold ? of vertical angular momentum has equation Cx = Cy = 0. It is a symplectic, codimension-2 submanifold, transverse to the Hamiltonian vector fields X Cx and X Cy of Cx and Cy. Since it is invariant by the flow of Quad, its tangent space has equations in the coordinates (xj , yj)j=1,...,4 of the proof of Lemma 10.3, x4 = y4 = 0. So, the upper-left 3 × 3 submatrix τ̃Quad of τQuad is the Hessian of the restriction of Quad to ?. In order to conclude, one merely needs to notice that the determinant of the torsion τ̃Quad:
is nonzero.
So, Quad (adequately truncated) has a nondegenerate quasiperiodic dynamics in the three degrees of freedom corresponding to coordinates (ψj , si)j=1,2,3.
End of the proof of Theorem 10.1. We would like to prove the persistence of some ofthe invariant tori of our normal form, which have frequencies of the following order (assuming a1 = O(1) and a2 →∞):
The conclusion thus follows from any of the four arguments below:
–the first item of Theorem 8.2 (using Proposition 10.6)
–the second item of Theorem 8.2 (using again Proposition 10.6), which yields not only the precedingly found Diophantine tori but also resonant tori (which induce Diophantine tori after reduction by the symmetry of rotation)
–the third item of Theorem 8.2 (using Proposition 10.4, for which the computation of the torsion is not needed, at the expense of deteriorating measure estimates)
–the fourth item of Theorem 8.2 (using again Proposition 10.4).
In three cases, the existence of Diophantine invariant tori of Kep + Quad is proved, either at the partially reduced level or at the fully reduced one. Locally, they will havepositive measure provided 
Theorem 8.2 applies with a perturbation ofthe size |H − Ko| = O(γN) for some N (Remark 7.9). Thus, the theorem really applies to the perturbation of the normal form of the Hamiltonian of order ∼ 7N/2 in 1 /a2.
Bibliographical comments.
–The discovery of the eccentricity vector is often wrongly attributed to Runge and Lenz [1].
–For an anachronistic proof of Bertrand’s theorem using Kolmogorov’s theorem, see [41].
–Lemma 10.2 is obvious in the plane problem, where the analogous reduction leads to a 2D reduced secular space, with coordinates (g1, G1) (see [35, 63]). This is less so in space. Harrington noticed it only after having carried out the computation [49]. Lidov–Ziglin [62] called this a “happy coincidence,” and indeed this invariance allowed them to study the bifurcation diagram of the quadrupolar Hamiltonian Quad. This was also crucial in various studies [53, 103, 104].
–Among the many accounts of the work of Lagrange and Laplace (comprising Lemma 10.3), we refer to [42, 58, 96].
–Resonance (10.6) of order 3 was known to Clairaut, noticed by Delaunay as un résultat singulier [26], and discovered by Herman in the general n-planet problem.
–In the proof of Lemma 10.5, it is a happy coincidence that resonant terms associated with the second resonance actually do not occur at our order of truncation. Malige has computed that higher degree resonant monomials occur, starting at order 10 [64].
–The strategy in Fejoz [37] for proving Arnold’s theorem corresponds to the third argument given above at the end of the proof of Theorem 10.1. The strategy of Chierchia–Pinzari [25] corresponds to the first and second arguments.
Let (X, ω) be a symplectic manifold, (φt)a symplectic flow, and T aminimal quasiperiodic invariant embedded torus for (φt).
Lemma A.1. If ω is exact, T is isotropic.
Proof. We may assume that φt(θ) = θ+tα (t ∈ ℝ, θ ∈ ?n) for some nonresonant vector α. Let
be the 2-form induced by ω on T. Since (φt) preserves ω, for all t, we have
Since the flow on T is minimal, νij is constant. By integrating with respect to θi and θj, this constant must be zero (more learnedly: according to the Hodge theorem, the zero 2-form is the unique harmonic representative of the cohomology class).
If ω is not exact, the conclusion may be wrong. M. Herman has even constructed codimension-2 minimal invariant tori, in such a robust manner that this disproved the quasi-ergodic hypothesis [99].
The following lemma is used in two instances in the proof of Lemma 2.1, as well as in the proof of Kolmogorov’s Theorem 6.5.
Lemma B.1 (Cohomological equation). Let s and σ be given in ]0, 1]. If 
there exists a unique function f ∈ ?(υ) of 0-average such that
and there exists a Cc = Cc(n, τ) such that, for any s, σ:
Proof. Up to substituting g − ∫?n g, we may assume that g has zero average. Then, let
be the Fourier expansion of g. The unique formal solutionto the equation Lαf = g is given by
Since g is analytic, its Fourier coefficients decay exponentially; thus, we find
by shifting the torus of integration to a torus Im θj = ±(s + σ) (the sign depending on the sign of kj). Using this estimate and replacing the small denominators k ⋅ α by its Diophantine lower bound, we get
where, as a change of variable and a rough approximation show, the latter sum is bounded by
Hence, f belongs to 
and satisfies the wanted estimate.
Bibliographical comments. The estimate has been obtained by bounding the terms of Fourier series one by one. In a more careful estimate, one should take into account the fact that if |k ⋅ α| is small, then k′ ⋅ α is not so small for neighboring k′’s. This makes it possible to find the optimal exponent of σ, uniformly with respect to the dimension [69, 81].
We have also used the following inverse function theorem. Recall that we have set 
Proposition B.2. Let 
The map id 
induces a map 
whose restriction 
has a unique right inverse 
Furthermore,
and, provided 2σ−1|υ|s+2σ ≤ 1,
Proof. Let 
be a continuous lift of id +υ and k ∈ Mn(ℤ), k(l) :=Φ(x + l) − Φ(x). Denote by 
the universal covering of
(i)Injectivity of 
Suppose that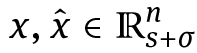 
and Φ(x) = Φ(x̂). By the mean value theorem,
hence, x = x̂.
(ii)Surjectivity of 
For any given 
the contraction
has a unique fixed point, which is apreimage of y by Φ.
(iii)Injectivity of 
Suppose that 
and φ(px) = φ(px̂), that is, Φ(x) = Φ(x̂) + κ for some κ ∈ ℤn. That k be in GL(n, ℤ), follows from the invertibility of Φ. Hence, Φ(x − k−1(κ)) = Φ(x̂), and, due to the injectivity of Φ, px = px̂.
(iv)Surjectivity of 
This is a trivial consequence of that of Φ.
(v)Estimate on 
Note that the wanted estimate on ψ follows from the corresponding estimate for the lifted map 
But, if 
,
hence, |Ψ − id |s ≤ |υ|s+σ.
(vi)Estimate on ψ′. We have ψ′ = φ′−1 ∘ φ, where φ′−1(x) stands for the inverse of the map ξ ↦ φ′′(x) ⋅ ξ. Hence,
and, under the assumption that 2σ−1|υ|s+2σ ≤ 1,
CInterpolation of spaces of analytic functions
In this section, we prove some Hadamard interpolation inequalities, which are used in Section 13.4.
Recall that we denote by 
infinite annulus ℂn/2πℤn, by 
thebounded subannulus 
| Im θj| ≤ s, j = 1, . . ., n} and by 
the polydisk {r ∈ ℂn, |rj| ≤ t, j = 1, . . ., n}. The supremum norm of a function f ∈ 
will be denoted by |f|s,t.
Let 0 < s0 ≤ s1 and 0 < t0 ≤ t1 be such that
Proposition C.1. If 
Proof. Let f ̃ be the function of 
constant on 2n-tori of equations (Im θ, |r|) = cst, defined by
(with all possible combinations of signs). Since log |f| is subharmonic (hence upper semicontinuous) and2n is compact, log f ̃ too is upper semicontinuous. Besides, log f ̃ satisfies the mean inequality; hence, it is plurisubharmonic.
By the maximum principle, the restriction of |f| to 
attains its maximum on the distinguished boundary of 
. Due to the symmetry of f ̃:
Now, the function
is well defined on ?s1 , for it is constant with respect to ℜz and, due to the relations imposed on the norm indices, if | Im z| ≤ s1, then |e−(iz+s)t| ≤ es1−s t = t1.
The estimate
trivially holds if Imz = s0 or s1, for, as noted above for j = 1, esj−s t = tj, j = 0, 1. But the left- and right-hand sides, respectively, are suharmonic and harmonic. Hence, the estimate holds whenever s0 ≤ Im z ≤ s1, whence the claim for z = is.
Recall that we have 
and, for a function 
let |f|s = |f|s,s denote its supremum norm on 
nAs in the rest of the paper, we now restrict the discussion to widths of analyticity ≤ 1.
In Section 13.4, we use the equivalent fact that, if 
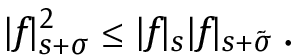
Proof. In Proposition C.1, consider the following particular case:
Then,
We want to determine max(s0, t0) and max(s1, t1). Let σ1 := s − s0 = s1 − s. Then, t0 = s e−σ1 and t1 = s eσ1 . The expression s + σ − seσ has the sign of σ (in the relevant region 0 ≤ s + σ ≤ 1, 0 ≤ s ≤ 1); by evaluating it at σ = ±σ1, we see that s0 ≤ t0 and s1 ≥ t1.
Therefore, since the norm | ⋅ |s,t is nondecreasing with respect to both s and t,
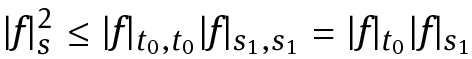
(thus giving up estimates uniform with respect to small values of s). By further setting σ0 = s − t0 = s (1 − e−σ1), we get the wanted estimate, and the asserted relation between σ0 and σ1 is readily verified.
Bibliographical comments.
–The obtained inequalities generalize the standard Hadamard inequalities. They are optimal and show that the convexity of analytic norms is twisted by the geometry of the phase space. See [72, Chap. 8] for more general but coarser inequalities.
–Interpolation inequalities in the analytic category do not depend on regularizing operators as they do in the Hölder or Sobolev cases. See, for example, [51, Theorem A.5] or [48].
Acknowledgment: These notes are the expanded version of a chapter of the Habilitation memoir [38] and of a subsequent short course given at the workshop Geometric control and related fields, organized by J.-B. Caillau and T. Haberkorn in RICAM (Linz, November 2014). I thank J.-B. Caillau, A. Chenciner, J. Mather, G. Pinzari and J.-C. Yoccoz for their interest or suggestions. Paradoxycally, this work has been partially funded by the ANR project Beyond KAM theory (ANR-15-CE40-0001)
Bibliography
[1]A. Albouy. Lectures on the two-body problem. In Classical and celestial mechanics (Recife, 1993/1999), pages 63–116. Princeton Univ. Press, Princeton, NJ, 2002.
[2]V. I. Arnold. Small denominators and problems of stability of motion in classical and celestial mechanics. Uspehi Mat. Nauk, 18(6 (114)):91–192, 1963.
[3]V. I. Arnold. Mathematical methods of classical mechanics, volume 60 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1989. Translated from the 1974 Russian original by K. Vogtmann and A. Weinstein, Corrected reprint of the second (1989) edition.
[4]V. I. Arnold, V. V. Kozlov, and A. I. Neishtadt. Mathematical aspects of classical and celestial mechanics, volume 3 of Encyclopaedia of Mathematical Sciences. Springer-Verlag, Berlin, third edition, 2006. Translated from the Russian original by E. Khukhro.
[5]A. Avila, B. Fayad, and R. Krikorian. A KAM scheme for SL(2, ℝ) cocycles with Liouvillean frequencies. Geom. Funct. Anal., 21(5):1001–1019, 2011.
[6]A. Avila and R. Krikorian. Reducibility or nonuniform hyperbolicity for quasiperiodic Schrödinger cocycles. Ann. of Math. (2), 164(3):911–940, 2006.
[7]V. I. Bakhtin. Averaging in multifrequency systems. Funktsional. Anal. i Prilozhen., 20(2):1–7, 96, 1986.
[8]V. Bernik, D. Kleinbock, and G. A.Margulis. Khintchine-type theorems on manifolds: the convergence case for standard and multiplicative versions. Internat. Math. Res. Notices, 9:453–486, 2001.
[9]M. Berti. Nonlinear oscillations of Hamiltonian PDEs. Progress in Nonlinear Differential Equations and their Applications, 74. Birkhäuser Boston Inc., Boston, MA, 2007.
[10]J. Bertrand. Théorème relatif au mouvement d’un point attiré vers un centre fixe. C. R. Math. Acad. Sci. Paris, 73:849–853, 1873.
[11]J.-B. Bost. Tores invariants des systèmes dynamiques hamiltoniens (d’après Kolmogorov, Arnold, Moser, Rüssmann, Zehnder, Herman, Pöschel, . . .). Astérisque, 1984/85(133–134):113–157, 1986. Séminaire Bourbaki.
[12]A. Bounemoura and S. Fischler. The classical KAM theorem for Hamiltonian systems via rational approximations. Regular and Chaotic Dynamics, 19:251–265, March 2014.
[13]J. Bourgain. Green’s function estimates for lattice Schrödinger operators and applications,volume 158 of Annals of Mathematics Studies. Princeton University Press, Princeton, NJ, 2005.
[14]R. C. Calleja, A. Celletti, and R. de la Llave. A KAM theory for conformally symplectic systems:efficient algorithms and their validation. J. Differential Equations, 255(5):978–1049, 2013.
[15]T. Castan. Complex singularities in the three-body problem and applications to stability andinstability. PhD thesis, Observatoire de Paris, 2016.
[16]A. Chenciner. Bifurcations de points fixes elliptiques. I. Courbes invariantes. Inst. Hautes Études Sci. Publ. Math., 61:67–127, 1985.
[17]A. Chenciner. Bifurcations de points fixes elliptiques. II. Orbites periodiques et ensembles de Cantor invariants. Invent. Math., 80(1):81–106, 1985.
[18]A. Chenciner. Bifurcations de points fixes elliptiques. III. Orbites périodiques de “petites” périodes et élimination résonnante des couples de courbes invariantes. Inst. Hautes Études Sci. Publ. Math., 66:5–91, 1988.
[19]A. Chenciner. Poincaré and the three-body problem. In Henri Poincaré, 1912–2012, volume 67 of Prog. Math. Phys., pages 51–149. Birkhäuser/Springer, Basel, 2015.
[20]C. Q. Cheng and Y. S. Sun. Existence of KAM tori in degenerate Hamiltonian systems. J. Differential Equations, 114(1):288–335, 1994.
[21]L. Chierchia. KAM lectures. In Dynamical Systems. Part I, Pubbl. Cent. Ric. Mat. Ennio Giorgi, pages 1–55. Scuola Norm. Sup., Pisa, 2003.
[22]L. Chierchia. A. N. Kolmogorov’s 1954 paper on nearly-integrable Hamiltonian systems.A comment on: “On conservation of conditionally periodic motions for a small change inHamilton’s function” [Dokl. Akad. Nauk SSSR (N.S.) 98:527–530, 1954]. Regul. Chaotic Dyn.,13(2):130–139, 2008.
[23]L. Chierchia and G. Pinzari. Properly-degenerate KAM theory (following V. I. Arnold). Discrete Contin. Dyn. Syst. Ser. S, 3(4):545–578, 2010.
[24]L. Chierchia and G. Pinzari. Planetary Birkhoff normal forms. J. Mod. Dyn., 5(4):623–664, 2011.
[25]L. Chierchia and G. Pinzari. The planetary N-body problem: symplectic foliation, reductions and invariant tori. Invent. Math., 186(1):1–77, 2011.
[26]C. Delaunay. Note sur les mouvements du périgée et du noeud de la lune. Comptes Rendus hebdomadaires des Séances de l’Académie des Sciences, 74:17, 1872.
[27]J. Lopes Dias. KAM theory as a limit of renormalization. In Dynamics, games and science. I, volume 1 of Springer Proc. Math., pages 253–270. Springer, Heidelberg, 2011.
[28]H. S. Dumas. The KAM story. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2014.
[29]I. Ekeland and É. Séré. Nash-moser without regularity. unpublished, 2012.
[30]L. H. Eliasson. Perturbations of stable invariant tori for Hamiltonian systems. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4), 15(1):115–147 (1989), 1988.
[31]L. H. Eliasson. Absolutely convergent series expansions for quasi periodic motions. Math. Phys. Electron. J., 2:Paper 4, 33 pp. (electronic), 1996.
[32]L. H. Eliasson, B. Fayad, and R. Krikorian. Kam-tori near an analytic elliptic fixed point. Regular and Chaotic Dynamics, 18(6):801–831, 2013.
[33]L. H. Eliasson, B. Fayad, and R. Krikorian. Around the stability of KAM tori. Duke Math. J., 164(9):1733–1775, 2015.
[34]A. Fathi. Weak Kam Theorem in Lagrangian Dynamics. Cambridge Univ. Press, 2007.
[35]J. Féjoz. Global secular dynamics in the planar three-body problem. Celestial Mech. Dynam. Astronom., 84(2):159–195, 2002.
[36]J. Féjoz. Quasiperiodic motions in the planar three-body problem. J. Differential Equations, 183(2):303–341, 2002.
[37]J. Féjoz. Démonstration du ‘théorème d’Arnold’ sur la stabilité du système planétaire (d’après Herman). Ergodic Theory Dynam. Systems, 24(5):1521–1582, 2004.
[38]J. Féjoz. Mouvements périodiques et quasi-périodiques dans le problème des n corps. Mémoire d’Habilitation de l’Université P. et M. Curie, 2010.
[39]J. Féjoz. A proof of the invariant torus theorem of Kolmogorov. Regular and Chaotic Dynamics, 17:1–5, 2012.
[40]J. Féjoz. On action-angle coordinates and the Poincaré coordinates. Regul. Chaotic Dyn., 18(6):703–718, 2013.
[41]J. Féjoz and L. Kaczmarek. Sur le théorème de Bertrand (d’après Michael Herman). Ergodic Theory Dynam. Systems, 24(5):1583–1589, 2004.
[42]J. Féjoz and S. Serfaty. Deux cents ans après Lagrange. Journée Annuelle, Paris, le 28 juin 2013. Société Mathématique de France, 2013.
[43]G. Forni. Solutions of the cohomological equation for area-preserving flows on compact surfaces of higher genus. Ann. of Math. (2), 146(2):295–344, 1997.
[44]G. Glaeser. Étude de quelques algèbres tayloriennes. J. Analyse Math., 6:1–124; erratum, insert to 6 (1958), no. 2, 1958.
[45]V. Guillemin and S. Sternberg. Convexity properties of the moment mapping. Invent. Math., 67:491–513, 1982.
[46]V. Guillemin and S. Sternberg. Symplectic techniques in physics. Cambridge University Press, Cambridge, second edition, 1990.
[47]B. Hall. Lie groups, Lie algebras, and representations, volume 222 of Graduate Texts in Mathematics. Springer, Cham, second edition, 2015. An elementary introduction.
[48]R. S. Hamilton. The inverse function theorem of Nash and Moser. Bull. Amer. Math. Soc. (N.S.), 7(1):65–222, 1982.
[49]R. S. Harrington. Dynamical evolution of triple stars. Astronom. J., pages 190–194, 1968.
[50]M. R. Herman. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publications Mathématiques de l’IHÉS, 49:5–233, 1979.
[51]L. Hörmander. The boundary problems of physical geodesy. Arch. Rational Mech. Anal., 62(1):1–52, 1976.
[52]H. Jacobowitz. Implicit function theorems and isometric embeddings. Ann. of Math. (2), 95:191–225, 1972.
[53]W. H. Jefferys and J. Moser. Quasi-periodic solutions for the three-body problem. Astronom. J., 71:568–578, 1966.
[54]D. Y. Kleinbock and G. A. Margulis. Flows on homogeneous spaces and Diophantine approximation on manifolds. Ann. of Math. (2), 148(1):339–360, 1998.
[55]A. Knauf. Mathematische Physik: Klassische Mechanik. Springer-Verlag, 2012.
[56]A. N. Kolmogorov. On the conservation of conditionally periodic motions for a small change in Hamilton’s function. Dokl. Akad. Nauk SSSR (N.S.), 98:527–530, 1954.
[57]S. B. Kuksin. Analysis of Hamiltonian PDEs, volume 19 of Oxford Lecture Series in Mathematics and its Applications. Oxford University Press, Oxford, 2000.
[58]J. Laskar. Sfogliando La Méchanique analitique, Giornata di studio su Louis Lagrange, chapter Lagrange et la stabilité du système solaire. Edizioni Universitarie di Lettere EconomiaDiritto, Milano, 2006.
[59]J. Laskar and P. Robutel. Stability of the planetary three-body problem. I. Expansion of the planetary Hamiltonian. Celestial Mech. Dynam. Astronom., 62(3):193–217, 1995.
[60]V. F. Lazutkin. Existence of a continuum of closed invariant curves for a convex billiard. Uspehi Mat. Nauk, 27(3(165)):201–202, 1972.
[61]V. F. Lazutkin. Existence of caustics for the billiard problem in a convex domain. Izv. Akad. Nauk SSSR Ser. Mat., 37:186–216, 1973.
[62]M. L. Lidov and S. L. Ziglin. Non-restricted double-averaged three body problem in Hill’s case. Celestial Mech., 13(4):471–489, 1976.
[63]B. B. Lieberman. Quasi-periodic solutions of Hamiltonian systems. J. Differential Equations, 11:109–137, 1972.
[64]F. Malige, P. Robutel, and J. Laskar. Partial reduction in the n-body planetary problem using the angular momentum integral. Celestial Mechanics and Dynamical Astronomy, 84:283–316, 2002. 10.1023/A:1020392219443.
[65]S. Marmi, P. Moussa, and J.-C. Yoccoz. Linearization of generalized interval exchange maps. Ann. of Math. (2), 176(3):1583–1646, 2012.
[66]J. E. Massetti. Quasi-periodicity and quasi-conservativity. PhD thesis, Observatoire de Paris, 2015.
[67]K. R. Meyer and G. R. Hall. Introduction to Hamiltonian Dynamical Systems and the N-Body Problem. Number vol. 90 in Applied Mathematical Sciences. Springer-Verlag, 1992.
[68]J. Moser. A new technique for the construction of solutions of nonlinear differential equations. Proc. Nat. Acad. Sci. U.S.A., 47:1824–1831, 1961.
[69]J. Moser. A rapidly convergent iteration method and non-linear differential equations. II. Ann. Scuola Norm. Sup. Pisa (3), 20:499–535, 1966.
[70]J. Moser. A rapidly convergent iteration method and non-linear partial differential equations.I. Ann. Scuola Norm. Sup. Pisa (3), 20:265–315, 1966.
[71]J. Moser. Convergent series expansions for quasi-periodic motions. Math. Ann., 169:136–176, 1967.
[72]R. Narasimhan. Several complex variables. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 1995. Reprint of the 1971 original.
[73]I. O. Parasyuk. Conservation of quasiperiodic motions of reversible multifrequency systems. Dokl. Akad. Nauk Ukrain. SSR Ser. A, 9:19–22, 85, 1982.
[74]I. O. Parasyuk. Preservation of multidimensional invariant tori of Hamiltonian systems. Ukrain. Mat. Zh., 36(4):467–473, 1984.
[75]R. Pérez-Marco. KAM techniques in PDE. Astérisque, 290:Exp. No. 908, ix, 307–317, 2003. Séminaire Bourbaki. Vol. 2001/2002.
[76]H. Poincaré. Les méthodes nouvelles de la mécanique céleste. Gauthier-Villars, 1892.
[77]G. Popov. KAM theorem for Gevrey Hamiltonians. Ergodic Theory Dynam. Systems, 24(5):1753–1786, 2004.
[78]J. Pöschel. A lecture on the classical KAM theorem. In Smooth ergodic theory and its applications (Seattle, WA, 1999), volume 69 of Proc. Sympos. Pure Math., pages 707–732. Amer. Math. Soc., Providence, RI, 2001.
[79]J. Pöschel. KAM à la R. Regul. Chaotic Dyn., 16(1–2):17–23, 2011.
[80]A. S. Pyartli. Diophantine approximations of submanifolds of a Euclidean space. Funkcional. Anal. i Priložen., 3(4):59–62, 1969.
[81]H. Rüssmann. On optimal estimates for the solutions of linear partial differential equations of first order with constant coefficients on the torus. In Dynamical systems, theory and applications, pages 598–624. Lecture Notes in Phys., Vol. 38. Springer, 1975.
[82]H. Rüssmann. On the existence of invariant curves of twist mappings of an annulus. In Geometric dynamics (Rio de Janeiro, 1981), volume 1007 of Lecture Notes in Math., pages 677–718. Springer, Berlin, 1983.
[83]H. Rüssmann. Nondegeneracy in the perturbation theory of integrable dynamical systems. InNumber theory and dynamical systems (York, 1987), volume 134 of London Math. Soc. LectureNote Ser., pages 5–18. Cambridge Univ. Press, Cambridge, 1989.
[84]H. Rüssmann. Nondegeneracy in the perturbation theory of integrable dynamical systems.In Stochastics, algebra and analysis in classical and quantum dynamics (Marseille, 1988), volume 59 of Math. Appl., pages 211–223. Kluwer Acad. Publ., Dordrecht, 1990.
[85]H. Rüssmann. On the frequencies of quasi-periodic solutions of analytic nearly integrable Hamiltonian systems. In Seminar on Dynamical Systems (St. Petersburg, 1991), volume 12 of Progr. Nonlinear Differential Equations Appl., pages 160–183. Birkhäuser, Basel, 1994.
[86]H. Rüssmann. Invariant tori in non-degenerate nearly integrable Hamiltonian systems. Regul. Chaotic Dyn., 6(2):119–204, 2001.
[87]F. Sergeraert. Un théorème de fonctions implicites sur certains espaces de Fréchet et quelques applications. Ann. Sci. École Norm. Sup. (4), 5:599–660, 1972.
[88]M. B. Sevryuk. The lack-of-parameters problem in the KAM theory revisited. In Hamiltoniansystems with three or more degrees of freedom (S’Agaró, 1995), volume 533 of NATO Adv. Sci.Inst. Ser. C Math. Phys. Sci., pages 568–572. Kluwer Acad. Publ., Dordrecht, 1999.
[89]M. B. Sevryuk. The classical KAM theory at the dawn of the twenty-first century. Mosc. Math. J., 3(3):1113–1144, 1201–1202, 2003. Dedicated to V. I. Arnold on the occasion of his 65th birthday.
[90]M. B. Sevryuk. The reversible context 2 in kam theory: the first steps. Regular and Chaotic Dynamics, 16(1):24–38, 2010.
[91]M. B. Sevryuk. Celestial Mechanics, chapter Classical Hamiltonian perturbation theory. Encyclopedia of life support systems. Unesco-EOLSS, 2015.
[92]C. L. Siegel and J. K. Moser. Lectures on celestial mechanics. Classics in Mathematics. Springer-Verlag, Berlin, 1995. Translated from the German by C. I. Kalme, Reprint of the 1971 translation.
[93]V. G. Sprindžuk. Achievements and problems of the theory of Diophantine approximations. Uspekhi Mat. Nauk, 35(4(214)):3–68, 248, 1980.
[94]E. M. Stein. Singular integrals and differentiability properties of functions. Princeton Mathematical Series, No. 30. Princeton University Press, Princeton, N.J., 1970.
[95]S. Sternberg. Celestial mechanics. Number v. 1 in Mathematics lecture note series. W. A. Benjamin, 1969.
[96]F. Tisserand. Traité de mécanique céleste. Gauthier-Villars, 1896.
[97]F. Wagener. A parametrised version of Moser’s modifying terms theorem. Discrete Contin. Dyn. Syst. Ser. S, 3(4):719–768, 2010.
[98]H. Whitney. Analytic extensions of differentiable functions defined in closed sets. Trans. Amer. Math. Soc., 36(1):63–89, 1934.
[99]J.-C. Yoccoz. Travaux de Herman sur les tores invariants. Astérisque, 206:Exp. No. 754, 4, 311–344, 1992. Séminaire Bourbaki, Vol. 1991/92.
[100]E. Zehnder. Generalized implicit function theorems with applications to some small divisor problems. I. Comm. Pure Appl. Math., 28:91–140, 1975.
[101]E. Zehnder. Generalized implicit function theorems with applications to some small divisor problems. II. Comm. Pure Appl. Math., 29(1):49–111, 1976.
[102]L. Zhao. Partial reduction and Delaunay/Deprit variables. Celestial Mech. Dynam. Astronom., 120:423–432, December 2014.
[103]L. Zhao. Quasi-periodic almost-collision orbits in the spatial three-body problem. Com. Pure App. Math., 2014.
[104]L. Zhao. Quasi-periodic solutions of the spatial lunar three-body problem. Celestial Mech. Dynam. Astronom., 119(1):91–118, 2014.