16Twist maps and Arnold diffusion for diffeomorphisms
Jean-Pierre Marco, Université Paris 6 (UMR 7586), 4 Place Jussieu, 75005 Paris cedex 05, jeanpierre. [email protected]
Abstract: We investigate a diffusion problem in the group ![]() of Cκ symplectic diffeomorphisms of the annulus ?2,with compact support contained in ?2×I2,where I ⊂ ℝ is a fixed interval containing [0, 1] in its interior. We endow
of Cκ symplectic diffeomorphisms of the annulus ?2,with compact support contained in ?2×I2,where I ⊂ ℝ is a fixed interval containing [0, 1] in its interior. We endow ![]() κ with the uniform Cκ topology.
κ with the uniform Cκ topology.
Let (θ, r) be the usual angle-action coordinates on ?2. We say that a diffeomorphism in![]() κ satisfies the diffusion property when it admits orbits whose action r1 starts close to 0 and later gets close to 1. Our problem is to describe the occurrence of the diffusion property in
κ satisfies the diffusion property when it admits orbits whose action r1 starts close to 0 and later gets close to 1. Our problem is to describe the occurrence of the diffusion property in ![]() κ.
κ.
We introduce the set ![]() ⊂
⊂ ![]() κ of diffeomorphisms of the form f(x1, x2) = (f1(x1),f2(x2)). The restriction of f1 to ? × [0, 1] is a symplectic twist map, which leaves the circles ?×{0} and ?×{1} invariant with Diophantine rotation, while f2 is a symplectic diffeomorphism that admits a hyperbolic fixed point O2 (whose expansion and contraction dominate those of f1) together with a transverse homoclinic point P2. For κ large enough, a diffeomorphism in
κ of diffeomorphisms of the form f(x1, x2) = (f1(x1),f2(x2)). The restriction of f1 to ? × [0, 1] is a symplectic twist map, which leaves the circles ?×{0} and ?×{1} invariant with Diophantine rotation, while f2 is a symplectic diffeomorphism that admits a hyperbolic fixed point O2 (whose expansion and contraction dominate those of f1) together with a transverse homoclinic point P2. For κ large enough, a diffeomorphism in κ does not satisfy the diffusion property and so, by analogy with the Hamiltonian setting for Arnold diffusion, it can be legitimately considered as an “unperturbed” system.
κ does not satisfy the diffusion property and so, by analogy with the Hamiltonian setting for Arnold diffusion, it can be legitimately considered as an “unperturbed” system.
Our main result, in the spirit of Arnold’s questions, is the following: when κ is large enough, given f ∈  κ, there is a ball Bκ(f, ε) in
κ, there is a ball Bκ(f, ε) in ![]() κ such that for any g ∈ Bκ(f, ε), there is a ̃g ∈
κ such that for any g ∈ Bκ(f, ε), there is a ̃g ∈ ![]() κ−1, arbitrarily close to g in the Cκ−1 topology, which satisfies the diffusion property.
κ−1, arbitrarily close to g in the Cκ−1 topology, which satisfies the diffusion property.
The diffeomorphisms we deal with here can be seen as models for Poincaré sections of near-integrable convex Hamiltonian systems in the neighborhood of double resonances, following the approach of [27].
16.1From Arnold diffusion to twist maps
The main concern of this paper is to exhibit a class of symplectic diffeomorphisms of ?2 = T∗?2 for which diffusion properties can be defined in a meaningful way and detected with minimal technicalities. Our framework is close to the “a priori chaotic” setting developed in relation to Mather’s work on unbounded growth of energy for nonautonomous perturbations of geodesic flows. This problem was investigated by Bolotin and Treschev [5] and Delshams et al. [12]; more recently Gelfreich and Turaev systematically revisited this question in the analytic category [20]. However, some significant features of our present paper are rather different and make our approach simpler.We work with finitely differentiable systems and consider perturbations of product diffeomorphisms of the form f(x1, x2) = (f1(x1), f2(x2)) with xi = (θi , ri) ∈ ?. Here f2 admits a hyperbolic fixed point with transverse homoclinic intersection and therefore a horseshoe, so our “unperturbed” system f already experiences the aforementioned “chaotic behavior.” Besides the finitely differentiable setting, the main differences compared with the previous studies come first from the assumptions on the factor f1, which we assume to be a general twist map (not necessarily close to integrable), and second from the compactness assumption on the support of our diffeomorphisms. Our motivation in introducing this setting is that it is a very good model for the dynamical behavior of near-integrable three-degree-of-freedom Hamiltonian systems in the neighborhood of double resonances, a key issue in the general problem of Arnold diffusion. In order to make this point more precise, we will first give a brief overview of recent results on this problem.
1. As usual, the annulus ?n = T∗?n is endowed with its natural angle-action coordinates (θ, r) and its exact symplectic form Ω. Hamiltonians h : ?n →ℝ, which depend only on the action variable r, play a particular role in the theory. The system generated by such an h leaves invariant each torus ?n × {r0}, r0 ∈ ℝn, and its restriction to ?n × {r0} is a constant vector field, so immediately integrated. A fundamental problem in Hamiltonian dynamics is to describe the qualitative behavior of the solutions of systems
where h and f are regular enough and f is small in some appropriate sense. KAMtheory proves the persistence of a large family of Lagrangian tori for such systems. The existence of more complex compact invariant subsets was then proved by Aubry, Mather, and Mañe by variational methods, further developed by Fathi in his weak KAM theory. The action variables on such invariant subsets remain bounded for all times. A natural question is, therefore, to understand the long-term variation of the actions for solutions whose initial conditions are not located in the union of the previous compact invariant subsets.
2. Arnold introduced in [1] the first example of an “unstable” Hamiltonian of the form (1.1) with n = 3:
where f is a suitably chosen trigonometric polynomial and where μ(ε) << ε. The main result of Arnold is the existence of ε0 > 0 such that for 0 < ε < ε0, the system Hε admits a solution γε(t) = (θ(t), r(t)) such that
for a suitable (large) Tε.
The key idea in the Arnold example is the construction of “chains of hyperbolic tori” along which the existence of drifting orbits can be proved. More precisely, a hyperbolic torus is a regular two-dimensional invariant torus, which admits stable and unstable three-dimensionalmanifolds (a “whiskered torus” in Arnold’s terminology). A chain is an ordered family (Tm)1≤m≤m∗ of hyperbolic tori, contained in a fixed energy level, such that the unstable manifold W−(Tm) intersects the stable manifold W+(Tm+1) transversely in that energy level. Under natural additional assumptions satisfied by the tori Tm, one can then apply a lambda-lemma to prove the existence of orbits of H ε shadowing the heteroclinic connections and passing close to each torus of the chain. Arnold moreover showed the existence of chains for which the extremal tori T1 and Tm∗ are located in the zones r1 < 0 and r1 > 1, respectively, which yields unstable solutions satisfying (1.3).
The Arnold example gave rise to a number of generalizations, following various approaches, see (among others) [2–5, 10–12, 15–20, 29, 35].
3. Arnold also conjectured that for “typical” systems of the form (1.1), the projection in action of some orbits should visit any element of a prescribed collection of small open sets centered on a connected component of a level set of h.
Let us be more specific and state that conjecture in the setting developped by Mather in [28]. Fix n ≥ 1. For 2 ≤ κ < +∞and f ∈ Cκ(?n) := Cκ(?n, ℝ) we let

and we set  so that
so that  is a Banach space.
is a Banach space.
The first problem is to make explicit the meaning of the rather unprecise word“typical” in Arnold’s conjecture. To apply variational methods, one restricts the setting to Tonelli unperturbedHamiltonians h, that is, functions which are strictly convex and satisfy a superlinear growth condition of the form lim‖r‖→∞ h(r)/‖r‖ = +∞. Then, a detailed analysis of the normal forms in various zones of the phase space shows that one cannot expect the required unstable behavior to appear generically in a whole ball centered at h: some particular loci have to be excluded a priori. This is in particular the case for a conical subset with vertex h, in the neighborhood of which specific hyperbolicity conditions in the normal forms are not satisfied.
Let us make this observation explicit. Let ?κ be the unit sphere in  Given afunction ε0 : ?κ →ℝ, one introduces the associated “generalized ball”:
Given afunction ε0 : ?κ →ℝ, one introduces the associated “generalized ball”:


The generalized balls are designed in such a way that the diffusion property can be expected to occur for a generic f inside them, provided that ε0 is properly chosen (Figure 1)36.
This yields the following version of the initial problem37.
Conjecture. Consider a Cκ integrable Tonelli Hamiltonian h on ?3. Fix an energy e larger than Min h and a finite family of open sets O1, . . . , Om which intersect h−1(e). Then for κ ≥ κ0 large enough, there exists a lower semicontinuous function
with positive values on an open dense subset of ?κ such that the subset of  for which the system
for which the system

admits an orbit which intersects each ?3 × Ok is open and dense in 
4. Recent advances toward a proof of this conjecture have been achieved (see [9, 18, 22, 27]). A common feature shared by all of them is the distinction between “simple resonance zones” and “double resonance zones” in the phase space of the system.
Fix a Tonelli Hamiltonian h and fix an energy e > Min h so that e is a regular value of h and h−1(e) is diffeomorphic to the Euclidean sphere S2. Then ω = ∇h : ℝ3 → ℝ3 is readily seen to be a diffeomorphism. With a given integer vector k ∈ ℤ3 is associated with a simple resonance curve at energy e, defined as the intersection

One easily sees that Γe(k) is diffeomorphic to a circle, and that two distinct such resonances intersect at exactly two points. One defines the double resonance points as the intersection points of two distinct simple resonance curves.

It turns out that the proofs of the Arnold conjecture involve only a finite number of simple resonance curves, and hence a finite number of double resonance points at their intersection38(Figure 2).
Normal forms are then performed along this “skeleton,” which naturally decomposes into “arcs of simple resonances” and “neighborhoods of double resonance points.” The dynamical features of these normal forms differ strongly according to this decomposition. The systems in the neighborhood of simple resonances are closely related to generalizations of Arnold’s initial example (1.2). The systems around double resonance points inherit a much richer geometric structure together with a somewhat simpler dynamical description, which is the concern of the present work.
5. The purpose of this paper is to introduce a class of systems, which are intimately related to the dynamical analysis of normal forms in the neighborhood of double resonances. Under suitable nondegeneracy conditions, this study essentially reduces to that of Poincaré return maps for sections diffeomorphic to compact subsets of ?2. Our model is designed to depict the main features of such sections and Poincaré maps, in such a way that “diffusion orbits” can be properly defined and correspond to what is needed to prove the existence of diffusion orbits for systems of the form (1.1).
More precisely, we consider the group ![]() κ of Cκ symplectic diffeomorphismsof the annulus ?2, with compact support contained in ?2 × I 2 (recall that the support of a diffeomorphism ϕ is the closure of the subset of all points which are not fixed by ϕ), where I ⊂ ℝis a fixed interval containing [0, 1] in its interior. We endow
κ of Cκ symplectic diffeomorphismsof the annulus ?2, with compact support contained in ?2 × I 2 (recall that the support of a diffeomorphism ϕ is the closure of the subset of all points which are not fixed by ϕ), where I ⊂ ℝis a fixed interval containing [0, 1] in its interior. We endow ![]() κ with the uniform topology, defined in the next section.
κ with the uniform topology, defined in the next section.
By analogy with (1.3), we say that diffeomorphism in ![]() κ satisfies the diffusion property when it admits a finite orbit such that the action r1 of its first point is close to 0 while that of its last point is close to 1. In our discrete model, the role of the unperturbed Hamiltonians h(r) in (1.1) is played by diffeomorphisms of a subset
κ satisfies the diffusion property when it admits a finite orbit such that the action r1 of its first point is close to 0 while that of its last point is close to 1. In our discrete model, the role of the unperturbed Hamiltonians h(r) in (1.1) is played by diffeomorphisms of a subset  κ(τ) ⊂
κ(τ) ⊂ ![]() κ (defined in the next section). These are diffeomorphisms of the form f(x1, x2) = (f1(x1), f2(x2)) with xi = (θi , ri) ∈ ?, where f1 is a symplectic twist map over ?×[0, 1] (with τ-Diophantine rotation on the boundaries) while f2 is a symplectic diffeomorphism that admits a hyperbolic fixed point O2 together with a transverse homoclinic point P2. We also require the Liapunov exponents of O2 to dominate the expansion and contraction rates of f2 (see condition (2.6)), which guarantees that ? × {O2} is a normally hyperbolic invariant annulus for f . One additional crucial property here is that? ×{P2} is a homoclinic annulus for? ×{O2}.
κ (defined in the next section). These are diffeomorphisms of the form f(x1, x2) = (f1(x1), f2(x2)) with xi = (θi , ri) ∈ ?, where f1 is a symplectic twist map over ?×[0, 1] (with τ-Diophantine rotation on the boundaries) while f2 is a symplectic diffeomorphism that admits a hyperbolic fixed point O2 together with a transverse homoclinic point P2. We also require the Liapunov exponents of O2 to dominate the expansion and contraction rates of f2 (see condition (2.6)), which guarantees that ? × {O2} is a normally hyperbolic invariant annulus for f . One additional crucial property here is that? ×{P2} is a homoclinic annulus for? ×{O2}.
We will show that a diffeomorphism f ∈  κ(τ) with κ large enough does not satisfy the diffusion property, and hence can be considered as an “unperturbed” system. Our main result (Theorem1) is directly related to (1.2) and its generalizations. Given an unperturbed system f ∈
κ(τ) with κ large enough does not satisfy the diffusion property, and hence can be considered as an “unperturbed” system. Our main result (Theorem1) is directly related to (1.2) and its generalizations. Given an unperturbed system f ∈  κ(τ), when κ is large enough, there exists a ball Bκ(f, ε) in
κ(τ), when κ is large enough, there exists a ball Bκ(f, ε) in ![]() κ such that for any g ∈ Bκ(f, ε), there is a ̃g ∈
κ such that for any g ∈ Bκ(f, ε), there is a ̃g ∈ ![]() κ−1, arbitrarily close to g in the Cκ−1 topology, which satisfies the diffusion property. It also turns out from our definition that the diffusion property is C0 open.
κ−1, arbitrarily close to g in the Cκ−1 topology, which satisfies the diffusion property. It also turns out from our definition that the diffusion property is C0 open.
6. The main point in our model is that proving the existence of diffusion orbits for ̃g amounts (up to a normally hyperbolic shadowing process) to proving the existence of connecting orbits for a bisystem (φ, ψ) of maps on some compact annulus A diffeomorphic to ? × [0, 1]. We will define these notions more precisely in the next section; we just need to say here that A will be contained in a normally hyperbolic annulus ![]() ∼ ? invariant by ̃g, φ will be a twist map, and ψ will describe the homoclinic excursions along the homoclinic connections of
∼ ? invariant by ̃g, φ will be a twist map, and ψ will describe the homoclinic excursions along the homoclinic connections of ![]() . The dynamics of the bisystem is defined as the result of the simultaneous iteration of both maps φ, ψ in arbitrary order. The “connecting orbits” are those which pass arbitrarily close to both boundaries of A. This study, which can be seen as a continuation of the Birkhoff theory of area preserving twist maps of A, was initiated by Moeckel in [29] in an abstract setting, and then continued in [23, 30]. As for the shadowing process, the main novelty here is the use of the Poincaré recurrence theorem for the map φ on the compact annulus A. This idea was initiated by De la Llave et al. [17] and makes our proof extremely simple.
. The dynamics of the bisystem is defined as the result of the simultaneous iteration of both maps φ, ψ in arbitrary order. The “connecting orbits” are those which pass arbitrarily close to both boundaries of A. This study, which can be seen as a continuation of the Birkhoff theory of area preserving twist maps of A, was initiated by Moeckel in [29] in an abstract setting, and then continued in [23, 30]. As for the shadowing process, the main novelty here is the use of the Poincaré recurrence theorem for the map φ on the compact annulus A. This idea was initiated by De la Llave et al. [17] and makes our proof extremely simple.
7. To a large extent, our approach to diffusion for systems (1.1) developed in [27] (and references therein) in the neighborhood of double resonances reduces to the same shadowing process based on the connecting properties of bisystems of twist maps and diffeomorphisms of ?. The present paper exhibits most of the essential features of the general problem and is moreover self-contained. A subsequent paper [24] is dedicated to a similar (but more involved) reduction of the diffusion problem along simple resonances to a shadowing based on the connecting properties of bisystems of twist maps and locally defined correspondences, which is the main concern of [18, 27].
Acknowledgment: I warmly thank L. Lazzarini for fruitful discussions on the symplectic geometry of normally hyperbolic manifolds, and S. Dumas, C. Labrousse for a careful reading and numerous improvements of the first version of this chapter. I also thank the referee for several useful remarks and improvements.
16.2Setting and main result
We fix once and for all a closed interval I ⊂ [−1, 2] of ℝ, which contains [0, 1] in its interior. Wework in the space ![]() κ of Cκ diffeomorphisms of?2 with support contained in ?2 × I2. We fix a lift I : ?2 → ℝ4 of the identity of ?2. We consider
κ of Cκ diffeomorphisms of?2 with support contained in ?2 × I2. We fix a lift I : ?2 → ℝ4 of the identity of ?2. We consider ![]() κ as a subset of
κ as a subset of  by lifting each φ ∈
by lifting each φ ∈ ![]() κ to the unique function ̃φ: ?2 → ℝ4, which coincides with I on ?2×[2,+∞[2.Wethen equip
κ to the unique function ̃φ: ?2 → ℝ4, which coincides with I on ?2×[2,+∞[2.Wethen equip ![]() κ with the induced topology, which is clearly defined by a metric dκ. The space (
κ with the induced topology, which is clearly defined by a metric dκ. The space (![]() κ , dκ) is complete.
κ , dκ) is complete.
We will first define a diffusion property for diffeomorphisms in ![]() κ. In parallel, we will introduce a specific class
κ. In parallel, we will introduce a specific class  κ(τ) ⊂
κ(τ) ⊂ ![]() κ,whose elements do not satisfy this property and which we consider as “unperturbed systems.” Our main result then proves the existence of a large subset of suitable C k−1 perturbations of f which admit the diffusion property.
κ,whose elements do not satisfy this property and which we consider as “unperturbed systems.” Our main result then proves the existence of a large subset of suitable C k−1 perturbations of f which admit the diffusion property.
1. Let us now give precise definitions, beginning with that of diffusion orbits.
Definition 1. Fix δ > 0 and set

Given a diffeomorphism g ∈ ![]() κ, we say that a finite orbit x0, . . . , x N of g is a δ-diffusion orbit when x0 ∈
κ, we say that a finite orbit x0, . . . , x N of g is a δ-diffusion orbit when x0 ∈ ![]() and xN ∈
and xN ∈ ![]() 1.
1.
2. The elements f ∈  κ(τ) are Cκ symplectic diffeomorphisms of ?2 and admit the product form
κ(τ) are Cκ symplectic diffeomorphisms of ?2 and admit the product form
where the diffeomorphisms fi : ? ![]() satisfy some additional conditions.
satisfy some additional conditions.
∙ We begin with the conditions on the first factor f1. We denote by D(τ) the set of real numbers which are Diophantine of exponent τ > 1:
Given κ ≥ 1 and τ > 1, we introduce the set  of Cκ symplectic diffeomorphisms f1 : ?
of Cκ symplectic diffeomorphisms f1 : ? ![]() , which satisfy the following conditions:
, which satisfy the following conditions:
(C1) Supp f1 ⊂ ?× I.
(C2) The circles Γ0 = ? × {0} and Γ1 = ? × {1} are invariant under f1, and their rotation numbers ρ0, ρ1 are in D(τ).
To introduce our third condition, in the coordinate chart (θ1, r1) of ?, we write

(C3) The restriction of f1 to the annulus ? × [0, 1] uniformly tilts the vertical to the right, that is, there is a c > 0 such that

Note that, due to (C1) and (C2), the annulus ?×[0, 1] is invariant under f1. The condition that the rotation numbers of the circles Γi are in D(τ) will ensure their persistence under perturbation.
∙ As for the second factor, we introduce the set  of Cκ symplectic diffeomorphisms f2 : ?
of Cκ symplectic diffeomorphisms f2 : ? ![]() which satisfy the following conditions:
which satisfy the following conditions:
(C4) Supp f2 ⊂ ?× I.
(C5) The diffeomorphism f2 possesses a hyperbolic fixed point O2.
(C6) The point O2 admits a transverse homoclinic point P2.
We will denote by

the maximal eigenvalue of the derivative DO2 f2. Note that O2 and P2 are contained in the support of f2.
3. We now define our set of “unperturbed” diffeomorphisms in order to guarantee additional stability properties under perturbations.
Definition 2. We define  κ(τ) as the set of (symplectic) diffeomorphisms on?2 of the form (2.2), where
κ(τ) as the set of (symplectic) diffeomorphisms on?2 of the form (2.2), where  and
and 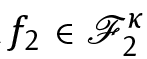 with
with
The domination condition (2.6) ensures that the invariant annulus ? × {O2} is uniformly normally hyperbolic for f , with persistence properties in the C κ topology and additional specific symplectic features (Figure 3).
4. Let us briefly show that given τ > 1, when κ is large enough, for any f ∈  κ(τ) there exists an arbitrarily small δ > 0 such that f does not possess a δ-diffusion orbit. An essential circle in? is a closed curve homotopic to ?×{0}. In the following, we denote by Ess(ϕ) the set of essential circles invariant under some diffeomorphism ϕ of ?.
κ(τ) there exists an arbitrarily small δ > 0 such that f does not possess a δ-diffusion orbit. An essential circle in? is a closed curve homotopic to ?×{0}. In the following, we denote by Ess(ϕ) the set of essential circles invariant under some diffeomorphism ϕ of ?.
Fix an f = (f1, f2) ∈  κ(τ). Then, thanks to Condition (C2) and assuming κ large enough, one deduces from Birkhoff’s normalization in the neighborhood of Γ0 (see [6, 14] and references therein for the continuous setting39)and classical KAM theorems inthe finitely differentiable setting [6, 34] the existence of an essential invariant circle Γlocated in the zone r1 > 0 (one indeed gets an infinite family of such circles). Hence there is an arbitrarily small δ > 0 such that Γ is located in the zone r1 > δ. Since f1 is assumed to have compact support, the connected components of the complement of Γ in? are invariant. This proves that f1 cannot admit an orbit with first point in the zone r1 < δ and last pointwith r1 close to 1. As a consequence, due to the product structure, the diffeomorphism f ∈
κ(τ). Then, thanks to Condition (C2) and assuming κ large enough, one deduces from Birkhoff’s normalization in the neighborhood of Γ0 (see [6, 14] and references therein for the continuous setting39)and classical KAM theorems inthe finitely differentiable setting [6, 34] the existence of an essential invariant circle Γlocated in the zone r1 > 0 (one indeed gets an infinite family of such circles). Hence there is an arbitrarily small δ > 0 such that Γ is located in the zone r1 > δ. Since f1 is assumed to have compact support, the connected components of the complement of Γ in? are invariant. This proves that f1 cannot admit an orbit with first point in the zone r1 < δ and last pointwith r1 close to 1. As a consequence, due to the product structure, the diffeomorphism f ∈  κ(τ) cannot admit a δ-diffusion orbit, which proves our claim.
κ(τ) cannot admit a δ-diffusion orbit, which proves our claim.

5. However, we will prove that under Cκ−1-dense small enough perturbations, any element of  κ(τ) gives rise to a diffeomorphism, which admits diffusion orbits. More precisely, our main result is the following.
κ(τ) gives rise to a diffeomorphism, which admits diffusion orbits. More precisely, our main result is the following.
Theorem 1. Fix τ > 1 and fix δ > 0. Then there is a κ0 such that if κ ≥ κ0, given f ∈  κ(τ), there is an ε(f) > 0 such that for any diffeomorphism g in Bκ(f, ε(f)) there exists a Cκ−1 diffeomorphism ̃g, arbitrarily close to g in the Cκ−1 topology, which admits a δ-diffusion orbit. Moreover, there is a neighborhood of ̃g in the C0 topology in which any diffeomorphism admits a δ-diffusion orbit.
κ(τ), there is an ε(f) > 0 such that for any diffeomorphism g in Bκ(f, ε(f)) there exists a Cκ−1 diffeomorphism ̃g, arbitrarily close to g in the Cκ−1 topology, which admits a δ-diffusion orbit. Moreover, there is a neighborhood of ̃g in the C0 topology in which any diffeomorphism admits a δ-diffusion orbit.
The existence of δ-diffusion orbits is clearly an open property in the C0 topology; we will therefore focus on the “density.” As mentioned in the introduction, similar results have already been obtained in related settings. One major difference is that we deal here with finitely differentiable maps. The loss of one derivative essentially comes from the fact that we have to consider the characteristic foliations of the stable and unstable manifolds of a Cκ normally hyperbolic annulus. These are Cκ hypersurfaces of ?2, so their characteristic foliations are Cκ−1 only. This problem has not been noticed before, due to the usual C∞ or analytic setting, together with the fact that the flow on the invariant annulus was assumed to be near-integrable, which increases the regularity of the various invariant manifolds at hand.
6. The proof of Theorem 1 is based on a method introduced by Moeckel in [29] to prove the existence of drifting orbits for bisystems of maps τ0, τ1 on the annulus. Given a set A, the formal definition of a bisystem (τ0, τ1) on A as a map τ : {0, 1}ℤ × A ![]() can be found in [25]. Here we will be content with the definition of its “projected orbits,” which are the result of the iteration of τ0 and τ1 on A in arbitrary order. More precisely, we say that a finite sequence (xn)0≤n≤n∗ of points of A is an orbit of the bisystem (τ0, τ1) when there exists a finite sequence (in)0≤n≤n∗−1 ∈ {0, 1}n∗ such that for 0 ≤ n ≤ n∗ − 1
can be found in [25]. Here we will be content with the definition of its “projected orbits,” which are the result of the iteration of τ0 and τ1 on A in arbitrary order. More precisely, we say that a finite sequence (xn)0≤n≤n∗ of points of A is an orbit of the bisystem (τ0, τ1) when there exists a finite sequence (in)0≤n≤n∗−1 ∈ {0, 1}n∗ such that for 0 ≤ n ≤ n∗ − 1
We can now state the two results by Moeckel we will use in the following. Given two disjoint essential circles Γ∙ and Γ∙ in ?, we denote by A[Γ∙ , Γ∙] ⊂ ? the subannulus bounded by their union.
Theorem A [29]. Let τ0, τ1 : ? ![]() be C1 exact-symplectic diffeomorphisms with compact support in ? × I. Assume that there exist two disjoint τ0-invariant essential circles Γ∙, Γ∙ in ? × I and that τ0 is a twist map in restriction to the annulus A := A[Γ∙ , Γ∙]. Let EssA(τ0) be the set of essential τ0-invariant circles contained in A. Assume that
be C1 exact-symplectic diffeomorphisms with compact support in ? × I. Assume that there exist two disjoint τ0-invariant essential circles Γ∙, Γ∙ in ? × I and that τ0 is a twist map in restriction to the annulus A := A[Γ∙ , Γ∙]. Let EssA(τ0) be the set of essential τ0-invariant circles contained in A. Assume that
Then for any connected neighborhoods U∙ and U∙ of Γ∙ and Γ∙ in ?, with τ1(Γ∙) ⊂ U∙ and τ1(Γ∙) ⊂ U∙ the bisystem (τ0, τ1)admitsan orbit with first point in U∙ and last point in U∙.
This in fact is a slight generalization of the theorem of [29], since the boundaries Γ∙ and Γ∙ are not assumed to be invariant under τ1. The proof follows almost exactly the same lines. One first introduces the full orbit of U∙ under the polysystem (τ0, τ1), that is, the union ![]() of all subsets of ? of the form
of all subsets of ? of the form
where n ≥ 0 is arbitrary. One then considers the connected component ![]() c of
c of ![]() ,which contains Γ∙ (this is the single difference with [29], where
,which contains Γ∙ (this is the single difference with [29], where ![]() is necessarily connected), and assume that the intersection A ∩
is necessarily connected), and assume that the intersection A ∩![]() c is disjoint from U∙. Up to the classical “filling the gaps” process, one gets from A∩
c is disjoint from U∙. Up to the classical “filling the gaps” process, one gets from A∩![]() c an invariant subset contained in AU∙, whose upper boundary is an essential circle invariant by both maps τ0 and τ1, which is a contradiction.
c an invariant subset contained in AU∙, whose upper boundary is an essential circle invariant by both maps τ0 and τ1, which is a contradiction.
The next result, based on the study of the Hausdorff dimension of the sets EssA(φ) and Ess(ψ), will provide us with the necessary tool for proving the density statement in Theorem 1.
Theorem B[29]. Fix an integer p ≥ 1. Let τ0, τ1 : ? ![]() be Cp exact-symplectic diffeomorphisms with compact support in ?×I. Assume that there exist two τ0-invariant disjoint essential circles Γ∙, Γ∙ in ?×I, and that τ0 is a twist map in restriction to A := A[Γ∙ , Γ∙]. Assume moreover that (τ0)|A has no essential invariant circle with rational rotation number. Then there exists a C∞ Hamiltonian h : ? → ℝ with support in?×I, arbitrarily small in the C∞ topology, such that
be Cp exact-symplectic diffeomorphisms with compact support in ?×I. Assume that there exist two τ0-invariant disjoint essential circles Γ∙, Γ∙ in ?×I, and that τ0 is a twist map in restriction to A := A[Γ∙ , Γ∙]. Assume moreover that (τ0)|A has no essential invariant circle with rational rotation number. Then there exists a C∞ Hamiltonian h : ? → ℝ with support in?×I, arbitrarily small in the C∞ topology, such that

where Φh stands for the time-one map of the Hamiltonian flow generated by h.
The proof is exactly the same as in [29].
16.3Proof of Theorem 1
Let us first informally describe the proof. The first ingredient is the choice of ε small enough so that any g in Bκ(f, ε(f)) exhibits some of the main dynamical features off. In particular, we require that g admits a normally hyperbolic invariant annulus ![]() gclose to ? ×{O2} and a homoclinic annulus
gclose to ? ×{O2} and a homoclinic annulus  close to? ×{P2}.
close to? ×{P2}.
We will then consider two diffeomorphisms of ![]() g.
g.
–The first one, which we denote by φg, is nothing but the restriction of g to ![]() g. Thanks to the domination condition (2.6) normally hyperbolic persistence proves that φg is Cκ close to f1 (in suitable coordinates). In particular, the initial invariant circles Γi of f1 will persist and give rise to essential invariant circles
g. Thanks to the domination condition (2.6) normally hyperbolic persistence proves that φg is Cκ close to f1 (in suitable coordinates). In particular, the initial invariant circles Γi of f1 will persist and give rise to essential invariant circles ![]() for φg, which bound a compact annulus Ag ⊂
for φg, which bound a compact annulus Ag ⊂ ![]() g.
g.
–The definition of the second diffeomorphism– the homoclinic map ψg–is based on the existence of the homoclinic annulus &&&&g. The diffeomorphism ψg encodes the asymptotic properties of the associated homoclinic orbits of ![]() g.More precisely, if x, y in
g.More precisely, if x, y in![]() g satisfy y = ψg(x), then there exists an orbit z−M, . . . , zN of g, located in ?2
g satisfy y = ψg(x), then there exists an orbit z−M, . . . , zN of g, located in ?2 ![]() g, with z−M arbitrarily close to
g, with z−M arbitrarily close to  and zN arbitrarily close to
and zN arbitrarily close to  where the integers N and M can be chosen arbitrarily large. A key observation (introduced in [17]) is that the Poincaré recurrence theorem applies toφg on the compact annulus
where the integers N and M can be chosen arbitrarily large. A key observation (introduced in [17]) is that the Poincaré recurrence theorem applies toφg on the compact annulus ![]() g and allows one to choose M and N so that
g and allows one to choose M and N so that  and
and 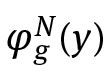 are arbitrarily close to the initial points x and y, respectively.
are arbitrarily close to the initial points x and y, respectively.
Using Moeckel’s results, we prove that after a small perturbation of g the bisystem (φg , ψg) admits “connecting orbits,” whose initial and final points are arbitrarily close to the boundary circles of Ag.
Finally, in view of the definition of φg and the asymptotic properties of ψg, one expects that the connecting orbits of the bisystem can be uniformly approximated by genuine orbits of g. We prove that this is the case, by means of normally hyperbolic shadowing lemma, whose idea is reminiscent of [5, 13].
16.3.1Choice of ε > 0
We refer to [7, 8, 21] for the definitions and main properties of (absolutely) normally hyperbolic manifolds, and in particular [8] for a presentation in the noncompact case for Lipschitzian maps. The results we use in the following are easy consequences of [7, 8]. Recall the usual notations and basic properties. Given g ∈ ![]() κ, a g-invariant submanifold
κ, a g-invariant submanifold ![]() g ⊂ ?2, and a subbundle E of TAg?2 invariant under Tg, we set
g ⊂ ?2, and a subbundle E of TAg?2 invariant under Tg, we set

Given an integer ℓ ∈ {1, . . . , κ}, the g-invariant manifold ![]() g is said to be ℓ-normally hyperbolic when there exist two Tg-invariant one-dimensional continuous subbundles E+, E− of TAg?2 satisfying
g is said to be ℓ-normally hyperbolic when there exist two Tg-invariant one-dimensional continuous subbundles E+, E− of TAg?2 satisfying

and such that

When this is the case, the manifold ![]() g is Cℓ and its stable and unstable manifolds W±(
g is Cℓ and its stable and unstable manifolds W±(![]() g) are well-defined and Cℓ too. These objects are persistent under Cκ perturbations of g, with Cℓ compact-open convergence to the unperturbed ones when the perturbation tends to 0. The stable and unstable manifolds W±(
g) are well-defined and Cℓ too. These objects are persistent under Cκ perturbations of g, with Cℓ compact-open convergence to the unperturbed ones when the perturbation tends to 0. The stable and unstable manifolds W±(![]() g) are foliated by the center-stable and unstable manifolds (W±(x))x∈Ag, which are Cℓ submanifolds of ?2. The regularity of the foliation itself is a more delicate matter; in the following we will take advantage of the symplectic features of our problem to get rid of these technicalities. Finally, normally hyperbolic manifolds enjoy natural local maximality properties.
g) are foliated by the center-stable and unstable manifolds (W±(x))x∈Ag, which are Cℓ submanifolds of ?2. The regularity of the foliation itself is a more delicate matter; in the following we will take advantage of the symplectic features of our problem to get rid of these technicalities. Finally, normally hyperbolic manifolds enjoy natural local maximality properties.
1. Let us first examine the dynamical structure of a diffeomorphism f ∈  κ(τ), which are immediately deduced from the product form (2.2).
κ(τ), which are immediately deduced from the product form (2.2).
–The annulus ![]() = ?×{O2} is invariant under f and diffeomorphic to ?. It is moreover κ-normally hyperbolic, due to condition (2.6): E ± are the stable and unstable lines of the fixed point O2 and
= ?×{O2} is invariant under f and diffeomorphic to ?. It is moreover κ-normally hyperbolic, due to condition (2.6): E ± are the stable and unstable lines of the fixed point O2 and

The stable and unstable manifolds of ![]() inherit the product structure of f :
inherit the product structure of f :

These are hypersurfaces of ?2 of class Cκ (since W±(O2) are Cκ). Their characteristic leaves are the one-dimensional submanifolds

–As a consequence of the normal hyperbolicity of ![]() , the manifolds W+(
, the manifolds W+(![]() ) and W−(
) and W−(![]() ) are foliated by the center-stable and center-unstable manifolds of the points of
) are foliated by the center-stable and center-unstable manifolds of the points of ![]() , respectively. In this trivial case these latter manifolds read
, respectively. In this trivial case these latter manifolds read

so they coincide with the characteristic leaves of W±(![]() ). Let Π± : W±(
). Let Π± : W±(![]() ) →
) → ![]() stand for the characteristic projections so that if (x, w) ∈ W±(x), then Π±(x, w) = (x, O2).
stand for the characteristic projections so that if (x, w) ∈ W±(x), then Π±(x, w) = (x, O2).
–ThelocalmanifoldsW±(![]() ) intersect transversely in ?2, along both
) intersect transversely in ?2, along both ![]() and the homoclinic annulus
and the homoclinic annulus
Moreover, for each (x, O2) ∈ ![]() , the leaf W −((x, O2)) transversely intersect the manifold W+(
, the leaf W −((x, O2)) transversely intersect the manifold W+(![]() ) at a unique point of &&&& , namely
) at a unique point of &&&& , namely

One has a similar observation for the stable leaves. We denote by π± the restrictions of Π± to the annulus &&&& so that

–Clearly ![]() and &&&& are symplectic submanifolds of ?2 and π± are symplectic diffeomorphisms.
and &&&& are symplectic submanifolds of ?2 and π± are symplectic diffeomorphisms.
–There exists a pair of natural f -induced symplectic diffeomorphisms of ![]() . The first one is just the restriction φ = f|A , which here admits a natural identification with f1. The second one is the map
. The first one is just the restriction φ = f|A , which here admits a natural identification with f1. The second one is the map
ψ = π+ ∘ (π−)−1,
which describes the homoclinic excursion of the orbits, we call it the homoclinic map40. Clearly ψ = Id here.
2. Our goal in this section is to prove the existence of an ε(f) small enough so that each g ∈ Bκ(f, ε(f)) admits a symplectic normally hyperbolic annulus endowed with a bisystem of symplectic maps defined in the same way as above.
Lemma 1. Let f = (f1, f2) ∈  κ(τ) be fixed. Then there exists
κ(τ) be fixed. Then there exists  such that for each
such that for each
–there exists a (uniquely defined) symplectic normally hyperbolic g–invariant annulus ![]() gof the form
gof the form
where ag is a Cκ function? → B2(O2, α) ⊂ ? such that ag − O2Cκ(?) → 0 when dκ(g, f) → 0 (where α > 0 is a suitable constant);
–the manifolds W±(![]() g) are coisotropic with characteristic foliations (W±(z))z∈Ag, and the characteristic projections
g) are coisotropic with characteristic foliations (W±(z))z∈Ag, and the characteristic projections
–there exists a (uniquely defined) symplectic homoclinic annulus &&&&g ⊂ W+(![]() g) ∩ W−(
g) ∩ W−(![]() g), of the form
g), of the form

where hg is a Cκ function? → B2(P2, α) ⊂ ? such that hg − P2Cκ(?) → 0 when dκ(g, f) → 0;
–the restrictions
 ±±
±±are Cκ−1 symplectic diffeomorphisms,
–for each z ∈ ![]() g, the center-unstable manifold W −(z) intersects &&&&g at
g, the center-unstable manifold W −(z) intersects &&&&g at  transversely in ?2, with a similar property for the center-stable manifold.
transversely in ?2, with a similar property for the center-stable manifold.
Sketch of proof. For ε small enough, the existence of the annulus ![]() g, together with the graph form(3.10), are direct consequences of the κ-normal hyperbolicity of
g, together with the graph form(3.10), are direct consequences of the κ-normal hyperbolicity of ![]() . We have implicitly used the local uniqueness related to normally hyperbolic manifolds: the annulus
. We have implicitly used the local uniqueness related to normally hyperbolic manifolds: the annulus ![]() g is the unique normally hyperbolic g-invariant manifold contained in a fixed small enough neighborhood of
g is the unique normally hyperbolic g-invariant manifold contained in a fixed small enough neighborhood of ![]() in ?2. The uniform estimates on the function ag come from the compact support condition on the diffeomorphism g. The local stable and unstable manifolds of
in ?2. The uniform estimates on the function ag come from the compact support condition on the diffeomorphism g. The local stable and unstable manifolds of ![]() g converge to those of
g converge to those of ![]() in the Cκ compact-open topology when dκ(g, f) → 0. Moreover, the compact support condition on g also yields uniform convergence along the first factor ?. The existence and form of &&&&g are immediate consequences of this latter observation.
in the Cκ compact-open topology when dκ(g, f) → 0. Moreover, the compact support condition on g also yields uniform convergence along the first factor ?. The existence and form of &&&&g are immediate consequences of this latter observation.
By normally hyperbolic persistence, there exist two uniquely defined Tg-invariant continuous subbundles E+, E− of TAg?2 such that TAg?2 = E+ ⊕T![]() g ⊕E−. Moreover, by continuous dependence, one can choose ε small enough so that
g ⊕E−. Moreover, by continuous dependence, one can choose ε small enough so that

It is not difficult to deduce from these conditions the existence of a neighborhood N of ![]() g in ?2 and positive constants c < 1 < C verifiying c C < 1, such that
g in ?2 and positive constants c < 1 < C verifiying c C < 1, such that

where  stand for the projections attached to the center-stable and center-unstable foliations. As a consequence, one easily proves that
stand for the projections attached to the center-stable and center-unstable foliations. As a consequence, one easily proves that ![]() g is symplectic, thatW±(
g is symplectic, thatW±(![]() g) are coisotropic, and that their characteristic foliations coincide with the center-stable and center-unstable foliations (see [26]).
g) are coisotropic, and that their characteristic foliations coincide with the center-stable and center-unstable foliations (see [26]).
From this latter property and the Cκ regularity of W±(![]() g), one deduces that themaps
g), one deduces that themaps  are Cκ−1.Moreover, the characteristic foliations of W±(
are Cκ−1.Moreover, the characteristic foliations of W±(![]() g) converge to thoseof
g) converge to thoseof ![]() in the Cκ−1 compact-open topology when dκ(g, f) → 0; with uniform convergence along the first factor. This yields the existence and uniqueness of an intersection point of W−(z) with &&&&g for z ∈
in the Cκ−1 compact-open topology when dκ(g, f) → 0; with uniform convergence along the first factor. This yields the existence and uniqueness of an intersection point of W−(z) with &&&&g for z ∈ ![]() g, with a similar property for W+(z). Hence the maps
g, with a similar property for W+(z). Hence the maps are diffeomorphisms, which are Cκ−1 since &&&&g itself is Cκ. These maps are induced by the intersection of characteristic foliations with symplectic sections ofW±(
are diffeomorphisms, which are Cκ−1 since &&&&g itself is Cκ. These maps are induced by the intersection of characteristic foliations with symplectic sections ofW±(![]() g), hence they are symplectic.
g), hence they are symplectic.
Moreover, assuming ε small enough, by Cκ−1 convergence to the unperturbedleaves, W−(z) intersects W+(![]() g) transversely at
g) transversely at  and W+(z) intersects W−(
and W+(z) intersects W−(![]() g) transversely at
g) transversely at 
![]()
3. We can now introduce our bisystem on ![]() g, assuming that
g, assuming that  We firstconsider the restriction
We firstconsider the restriction

which is a Cκ symplectic diffeomorphism for the induced structure on ![]() g. As for oursecond map, we set
g. As for oursecond map, we set

Therefore ψg is a Cκ−1 symplectic map. The next lemma will enable us to identify φg(and ψg) with a diffeomorphism of the standard annulus ? in a proper way.
Lemma 2. If  is small enough, there exists a C κ−1 symplectic embeddingΦg of ?, equipped with the standard form, into ?2 such that
is small enough, there exists a C κ−1 symplectic embeddingΦg of ?, equipped with the standard form, into ?2 such that
–Φg(?) = ![]() g;
g;
–the diffeomorphism  has support in ?× I and tends to f1in the Cκ−1 uniform topology when dκ(g, f) → 0.
has support in ?× I and tends to f1in the Cκ−1 uniform topology when dκ(g, f) → 0.
–the diffeomorphism  has support in ?× I and tends to Id in the C κ−1 uniform topology.
has support in ?× I and tends to Id in the C κ−1 uniform topology.
Proof. The map Ψg : x1 ↦ (x1, ag(x1)) is a Cκ embedding of ? into ?2 with image ![]() g, which converges to the embedding J : x1 ↦ (x1, O2) when g → f. Hence the diffeomorphism
g, which converges to the embedding J : x1 ↦ (x1, O2) when g → f. Hence the diffeomorphism  tends to f1 in the Cκ uniform topology when dκ(g, f) → 0.
tends to f1 in the Cκ uniform topology when dκ(g, f) → 0.
Using Moser’s isotopy argument, one proves the existence of a Cκ−1 diffeomorphism Cg : ? ![]() , which sends the standard symplectic form on ? onto the pullback
, which sends the standard symplectic form on ? onto the pullback of the induced form on
of the induced form on ![]() g. This loss of regularity comes from the fact that
g. This loss of regularity comes from the fact that only. One also proves that Cg → Id in the uniform Cκ−1 topology when dκ(g, f) → 0.
only. One also proves that Cg → Id in the uniform Cκ−1 topology when dκ(g, f) → 0.
Hence Φg = Ψg ∘ Cg : ? → ![]() g is symplectic (where ? is endowed with the standard form), and Φg → J in the uniform Cκ−1 topology when dκ(g, f) → 0. Our claim easily follows.
g is symplectic (where ? is endowed with the standard form), and Φg → J in the uniform Cκ−1 topology when dκ(g, f) → 0. Our claim easily follows.
The following corollary is an immediate application of the previous lemma and finitely differentiable KAM theory [6, 34].
Corollary 1. There is an  such that for each diffeomorphism g ∈ Bκ(f, ε(f)) there exist a Cκ−1 symplectic embedding Φg of ? into
such that for each diffeomorphism g ∈ Bκ(f, ε(f)) there exist a Cκ−1 symplectic embedding Φg of ? into ![]() g such that the map ̂φg = Φ−1 ∘ φg ∘ Φ admits two (disjoint) essential invariant circles Γ∙ and Γ∙ with rotation numbers ρ0 and ρ1, respectively (see (C2)), such that Γ∙ → Γ0 and Γ∙ → Γ1 in the C0 topology when dκ(g, f) → 0. Moreover, the map ̂φg uniformly tilts the vertical over the annulus Ag bounded by Γ∙ and Γ∙.
g such that the map ̂φg = Φ−1 ∘ φg ∘ Φ admits two (disjoint) essential invariant circles Γ∙ and Γ∙ with rotation numbers ρ0 and ρ1, respectively (see (C2)), such that Γ∙ → Γ0 and Γ∙ → Γ1 in the C0 topology when dκ(g, f) → 0. Moreover, the map ̂φg uniformly tilts the vertical over the annulus Ag bounded by Γ∙ and Γ∙.
16.3.2Implementation of Moeckel’s method
We fix now a diffeomorphism g ∈ Bκ(f, ε(f)), where ε(f) is defined in Corollary 1, and we want to prove the existence of a perturbed diffeomorphism ̃g ∈ Bκ(f, ε(f)), arbitrarily close to g in the Cκ−1 topology, for which the associated bisystem (φ̃g , ψ̃g) satisfies condition (2.7). We proceed in two steps: we first perturb g so that φg has no rational essential circle, and we then perturb the resulting diffeomorphism again (without perturbing φg) to ensure condition (2.7). We write ε instead of ε(f) in the following.
16.3.2.1 First perturbation of g: making φg admissible
Let J be a closed interval of ℝ containing [0, 1] in its interior and contained in theinterior of I. By usual perturbation techniques (see [31, 32]), there exists a Cκ diffeomorphism ̂g ∈ Bκ(f, ε), arbitrarily close to g in the uniform Cκ topology, which satisfies
–the invariant annulus ![]() ̂g coincides with
̂g coincides with ![]() g;
g;
–all periodic points of φ̂g = ̂g|Âg in ?2 × J2 are either hyperbolic or elliptic with nondegenerate Birkhoff invariant.
As a consequence, if κ is large enough to ensure the existence of invariant curvessurrounding each elliptic point, one easily proves that φ̂g cannot admit an essential invariant circle with rational rotation number in the compact annulus Âg defined in Corollary 1.
16.3.2.2 Second perturbation of g: making ψg admissible
In view of the last section, replacing g with ̂g, we can assume that g has no invariant circle in Ag with rational rotation number. We want now to perturb g into a new diffeomorphism ̃g such that

We first analyze the composition of g with a diffeomorphism with support localized ina small enough neighborhood of the annulus &&&&g.
Lemma 3. Let  be the submanifolds (diffeomorphic to [0, 1]×?) of W±(
be the submanifolds (diffeomorphic to [0, 1]×?) of W±(![]() g) boundedby
g) boundedby ![]() g and &&&&g. Let N be a neighborhood of &&&&g such that
g and &&&&g. Let N be a neighborhood of &&&&g such that
Assume that χ is a diffeomorphism of ?2 with support in N , which leaves the annulus&&&&g invariant, and set ̃g = χ ∘ g. Then ![]() ̃g =
̃g = ![]() g,&&&&̃g = &&&&g and
g,&&&&̃g = &&&&g and
Proof. By (3.19), ![]() g is still invariant and normally hyperbolic under ̃g, since g and ̃g coincide in a tubular neighborhood of
g is still invariant and normally hyperbolic under ̃g, since g and ̃g coincide in a tubular neighborhood of ![]() g. Therefore
g. Therefore ![]() g =
g = ![]() ̃g and φ̃g = φg. We will write W±(
̃g and φ̃g = φg. We will write W±(![]() ̃g , ̃g) for the stable and unstable manifolds of
̃g , ̃g) for the stable and unstable manifolds of ![]() g with respect to the diffeomorphism ̃g.
g with respect to the diffeomorphism ̃g.
Set  By (3.19) g and ̃g coincide on
By (3.19) g and ̃g coincide on  hence
hence  and therefore
and therefore
Set now  Then, again by (3.19),
Then, again by (3.19),  and
and
We assumed&&&&g = χ(&&&&g). Hence, since (
(![]() ̃g , ̃g) by (3.22).Moreover,
̃g , ̃g) by (3.22).Moreover,  by (3.21). As a consequence,
by (3.21). As a consequence,
is still a homoclinic annulus for ![]() ̃g. We set &&&& = &&&&̃g = &&&&g.
̃g. We set &&&& = &&&&̃g = &&&&g.
Let  be the characteristic ±projections, with similar notation for ̃g. Then
be the characteristic ±projections, with similar notation for ̃g. Then

Set &&&& 1 = g(&&&& ) and observe ++that by (3.19). Then
by (3.19). Then

where we used (3.19) again in the second equality. Hence

As for the unstable projections, set now &&&& −1 = g−1(&&&& ) and observe that

Now

and

so that

Finally, since 

which concludes the proof.
We can now use Moeckel’s Theorem B in order to produce our perturbation ̃g.
Lemma 4. There exists a diffeomorphism ̃g ∈ ![]() κ−1, arbitrarily close to g in the Cκ−1 topology such that
κ−1, arbitrarily close to g in the Cκ−1 topology such that ![]() ̃g =
̃g = ![]() g, φ̃g = φg and the maps τ0 = φg and τ1 = ψ̃g satisfy Condition (2.7) of Theorem A.
g, φ̃g = φg and the maps τ0 = φg and τ1 = ψ̃g satisfy Condition (2.7) of Theorem A.
Proof. Let ϕ := Φg : ? → ![]() g be the symplectic embedding exhibited in Lemma 2,and set
g be the symplectic embedding exhibited in Lemma 2,and set

By Theorem B, there exists a C∞ Hamiltonian h : ? → ℝarbitrarily close to 0 suchthat ̂φg and the modified diffeomorphism

satisfy (2.7).
In view of Lemma 3, equation (3.20), let us introduce the perturbed diffeomorphism

where χ : &&&&g ![]() is a diffeomorphism we want to determine (and which we will have to continue to a diffeomorphism χ defined in a neighborhood of &&&&g in the following). Set
is a diffeomorphism we want to determine (and which we will have to continue to a diffeomorphism χ defined in a neighborhood of &&&&g in the following). Set

We want to choose χ in order to solve the equation

Straightforward computation yields

where ℓ = h ∘ ϕ−1.
Therefore χ is a Cκ−1 Hamiltonian diffeomorphism of the annulus &&&&g, with compact support, which tends to Id in the Cκ−1 topology when dκ(g, f) → 0. As a consequence, there is a Cκ function ξ : ℝ×&&&&g →ℝ, with support in ]0, 1[ ×&&&&g such that

where Φξ is the time-one map starting at 0 generated by ξ. Using the Moser isotopy argument, one proves the existence of a Cκ−1 symplectic diffeomorphism

where N is a neighborhood of &&&&g in ?2, α is a positive constant, and the first factor is endowed with the usual symplectic structure. Fix a C∞ bump function η : B2(0, α) → ℝ equal to 1 in a neighborhood of 0 and define a function L : ℝ×?×B2(0, α) → ℝby

Then clearly the time-one map χ = T ∘ ΦL leaves &&&&g invariant, with χ|Hg = χ and the support of χ is contained in N . Moreover, χ tends to the identity in the Cκ−1 topology when ℓ tends to 0 in the Cκ topology. Setting ̃g = χ ∘ g provides us with the perturbed diffeomorphism we were looking for.
16.3.3Normally hyperbolic shadowing
The aim of this section is to prove the following result, from which our main theorem easily follows. Let d stand for the product metric on ?2.
Theorem 2. Fix f ∈  κ(τ) with κ so that the statements of the last section hold. Fix g in Bκ(f, ε(f)) and fix an orbit x0, . . . , xn of the polysystem (φg , ψg) on
κ(τ) with κ so that the statements of the last section hold. Fix g in Bκ(f, ε(f)) and fix an orbit x0, . . . , xn of the polysystem (φg , ψg) on ![]() g. Then for any δ > 0 there is an orbit z0, . . . , zN of g in ?2 such that d(z0, x0) < δ and d(zN , xn) < δ. One can moreover choose z0 so that for each i ∈ {0, . . . , n}, there is an m(i) with
g. Then for any δ > 0 there is an orbit z0, . . . , zN of g in ?2 such that d(z0, x0) < δ and d(zN , xn) < δ. One can moreover choose z0 so that for each i ∈ {0, . . . , n}, there is an m(i) with

One main ingredient in the proof is the Poincaré recurrence theorem, following an idea introduced in [17]. Since φg has compact support and preserves the symplectic area on ![]() g, by the Poincaré recurrence theorem almost every point of
g, by the Poincaré recurrence theorem almost every point of ![]() g is positively and negatively recurrent for φg. In the following we use recurrent as a shorthand for positively and negatively recurrent.
g is positively and negatively recurrent for φg. In the following we use recurrent as a shorthand for positively and negatively recurrent.
The other main tool of the proof is the following λ-lemma.
Normally hyperbolic inclination lemma. Fix f ∈  κ(τ) with κ so that the statements of the last section hold, and fix g in B(f, ε(f)). Let (jx)x∈Ag be a continuous family of C1 parametrizations of the local center-unstable manifolds attached to
κ(τ) with κ so that the statements of the last section hold, and fix g in B(f, ε(f)). Let (jx)x∈Ag be a continuous family of C1 parametrizations of the local center-unstable manifolds attached to ![]() g, that is, a C0 map j :
g, that is, a C0 map j : ![]() g × [−1, 1] → W−(
g × [−1, 1] → W−(![]() g) such that, setting jx = j(x, ⋅)
g) such that, setting jx = j(x, ⋅)

and jx is C1. Then for any C1 submanifold Δ of ?2 which intersects W+(![]() g) transversely in ?2 at some point ξ ∈ W+(x), there exist a sequence (Δn)n∈ℕ such that
g) transversely in ?2 at some point ξ ∈ W+(x), there exist a sequence (Δn)n∈ℕ such that

and for n ∈ ℕ, a C1 diffeomorphism ℓn : [−1, 1] → gn(Δn) such that

We refer to [33] for a proof with detailed estimates in the compact setting, which directly applies here, thanks to our compactness assumption on the support of g.
Proof of Theorem 2. We will write φ, ψ instead of φg, ψg. Fix an orbit x0, . . . , xn of the polysystem (φ, ψ) on ![]() g and fix δ > 0. We fix a tubular neighborhood N of
g and fix δ > 0. We fix a tubular neighborhood N of ![]() g in ?2 such that N ∩ W−(
g in ?2 such that N ∩ W−(![]() g) is invariant by g−1 and for each z ∈ N ∩ W−(
g) is invariant by g−1 and for each z ∈ N ∩ W−(![]() g) with z ∈ W−(y):
g) with z ∈ W−(y):

Setting τ0 = φ and τ1 = ψ, by definition, there exists a sequence ω0, . . . , ωn−1 in {0, 1} such that for 0 ≤ j ≤ n − 1

Choose r > 0 small enough so that if D0 = ![]() g ∩ B(x0, r) and if
g ∩ B(x0, r) and if

then Dj ⊂ ![]() g ∩ B(xj , δ/2) for 0 ≤ j ≤ n (which is possible by continuity of both maps τj).
g ∩ B(xj , δ/2) for 0 ≤ j ≤ n (which is possible by continuity of both maps τj).
We will prove the existence of an orbit (yj)1≤j≤n of (τ0, τ1) associated with the same sequence (ωj) such that the point yj belongs to Dj and is recurrent for τ0 = φ, and the existence of a sequence of balls (Bj)0≤j≤n of ?2, which satisfy the following two properties:
∙ (Cj): for 0 ≤ j ≤ n, Bj is centered at some point zj ∈ W−(yj) ∩ N and Bj ⊂ B(yj , δ/2),
∙ (Tj): for 0 ≤ j ≤ n − 1, ∃mj > 0 such that gmj (Bj) ⊂ Bj+1.
We will construct these objects backward, by finite induction. It is enough to prove that given some recurrent point yj+1 ∈ Dj+1 together with a ball Bj+1 satisfying (Cj+1), one can find a recurrent point yj ∈ Dj, a ball Bj satisfying (Cj), and a positive mj which satisfies (Tj).
1. Assume first that xj+1 = φ(xj), so Dj+1 = φ(Dj). By assumption, the point yj+1 ∈ Dj+1 is recurrent for φ, hence the point yj = φ−1(yj+1) is in Dj and is recurrent for φ too. By (Cj+1), the ball Bj+1 is centered at some zj+1 ∈ W−(yj+1). By our assumption on W−(![]() g) ∩ N and since g coincides with φ on
g) ∩ N and since g coincides with φ on ![]() g, setting zj = g−1(zj+1),
g, setting zj = g−1(zj+1),

Therefore, by continuity of g, there exists a ball Bj centered at zj and contained in B(yj , δ/2) such that g(Bj) ⊂ Bj+1.
2. Assume now that xj+1 = ψ(xj) so that Dj+1 = ψ(Dj). Let Rj and Rj+1 be the fullmeasure subsets of Dj and Dj+1 formed by the recurrent points for φ. Since ψ is measure-preserving, Rj+1 ∩ ψ(Rj ) is a full measure subset of Dj+1. Therefore, there exists a recurrent point yj ∈ Rj such that yj+1 = ψ(yj) is recurrent, and so close to yj+1 that, by continuity of the center-unstable foliation, the leaf W−(yj+1) intersects the ball Bj+1. By definition of ψ and by the last item in Lemma 1, the submanifold Δ = W−(yj) intersects W+(![]() g) transversely in ?2 at some point ξ ∈ W+(yj+1). Apply the inclination lemma to Δ in the neighborhood of ξ, together with the positive recurrence property of yj+1: there exists an arbitrarily large integer m′′ such that gm′ (Δ) intersects Bj+1. Fix
g) transversely in ?2 at some point ξ ∈ W+(yj+1). Apply the inclination lemma to Δ in the neighborhood of ξ, together with the positive recurrence property of yj+1: there exists an arbitrarily large integer m′′ such that gm′ (Δ) intersects Bj+1. Fix

then

Now, by definition of and since
and since ![]() is negatively recurrent, there is an (arbitrarilylarge) integer m″ such that
is negatively recurrent, there is an (arbitrarilylarge) integer m″ such that

Set  so that yj is recurrent and the point zj = g−(m″+m′)(z) ∈ W−(yj)satisfies
so that yj is recurrent and the point zj = g−(m″+m′)(z) ∈ W−(yj)satisfies
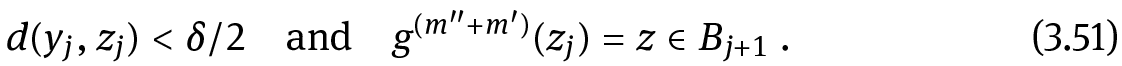
Hence by continuity there exists a ball Bj centered at zj such that conditions (Cj) and (Tj) are satisfied.
3.As a consequence, there exists a sequence of integers (mi )1≤≤n such that for 1 ≤ i ≤ n
By construction, any z0 ∈ B0 satisfies our statement.![]()
16.3.4Conclusion of the proof of Theorem 1
Fix f ∈  κ(τ) and δ > 0.We assume that κ is large enough so that all the conclusions of the last sections hold. Set
κ(τ) and δ > 0.We assume that κ is large enough so that all the conclusions of the last sections hold. Set

By Lemma 2 and Corollary 1, one can choose ε ∈ ]0, ε(f)[ small enough so that for any diffeomorphism g ∈ B(f, ε), with the notation of Lemma 2, the invariant circles Γ∙ and Γ∙ of ̂φg satisfy

and are such that moreover

We then proved the existence of a C κ−1 diffeomorphism ̃g ∈ B(f, ε(f)) arbitrarily close to g in the Cκ−1 topology, which admits the same annulus ![]() g and such that the bisystem (φ̃g , ψ̃g) associated with ̃g satisfies (2.7). In particular, (φ̃g , ψ̃g) admits an orbit with first point in
g and such that the bisystem (φ̃g , ψ̃g) associated with ̃g satisfies (2.7). In particular, (φ̃g , ψ̃g) admits an orbit with first point in ![]() ∙ and last point in
∙ and last point in ![]() ∙. Theorem 2 applied with δ/2 instead of δ to the bisystem (φ̃g , ψ̃g) and the previous orbit produces an orbit of ̃g with first point in
∙. Theorem 2 applied with δ/2 instead of δ to the bisystem (φ̃g , ψ̃g) and the previous orbit produces an orbit of ̃g with first point in ![]() 0 and last point in
0 and last point in ![]() 1 (see Definition 1). This concludes the proof.
1 (see Definition 1). This concludes the proof.
Bibliography
[1]V. I. Arnold, “Instability of dynamical systems with several degrees of freedom.” Soviet Math. Doklady 5:581–585, 1964.
[2]P. Bernard. “The dynamics of pseudographs in convex Hamiltonian systems.” J. Amer. Math. Soc. 21(3):615–669, 2008.
[3]P. Bernard. “Large normally hyperbolic cylinders in a priori stable Hamiltonian systems.” Ann. Henri Poincaré 11(5):929–942, 2010.
[4]P. Bernard, V. Kaloshin, K. Zhang. “Arnold diffusion in arbitrary degrees of freedom and crumpled 3-dimensional normally hyperbolic invariant cylinders.” arXiv:1112.2773.
[5]S. Bolotin, D. Treschev. “Unbounded growth of energy in nonautonomous Hamiltonian systems.” Nonlinearity 12:365–387, 1999.
[6]A. Bounemoura. “Non-degenerate Liouville tori are KAM stable.” Preprint.
[7]A Bounemoura, P. Berger. “A geometrical proof of the persistence of normally hyperbolic submanifolds.” Dynamical Systems: An International Journal 28(4):567–581, 2013.
[8]M. Chaperon. “The Lipschitz core of some invariant manifold theorems.” Ergodic Theory and Dynamical Systems 28:1419–1441, 2008.
[9]C. Q. Cheng. “Arnold diffusion in nearly integrable Hamiltonian systems.” arXiv:1207.4016.
[10]C. Q. Cheng. J. Yan. “Arnold diffusion in Hamiltonian systems: a priori unstable case.” J. Differential Geom. 82(2):229–277, 2009.
[11]A. Delshams, R. de la Llave, T. Seara. “A geometric mechanism for diffusion in Hamiltonian systems overcoming the large gap problem.” Memoirs AMS., 179, 2006.
[12]A. Delshams, R. de la Llave, T. Seara. “Orbits of unbounded energy in quasi-periodic perturbations of geodesic flows.” Adv. Math. 202(1):64–188, 2006.
[13]A. Delshams, R. de la Llave and T. M. Seara. “Geometric properties of the scattering map of a normally hyperbolic invariant manifold.” Adv. Math. 217(3):1096–1153, 2008.
[14]L. H. Eliasson, B. Fayad, and R. Krikorian. “Around the stabiity of KAM tori.” Duke Math. J. 164(9):1733–1775, 2015.
[15]E. Fontich, P. Martin. “Hamiltonian systems with orbits covering densely submanifolds of small codimension”. Nonlinear Analysis 52:315–327, 2003.
[16]M. Gidea, R. de la Llave. “Topological methods in the instability problem of Hamiltonian systems.” Discrete Contin. Dyn. Syst. 14(2):295–328, 2006.
[17]M. Gidea, R. de la Llave, T. Seara. “A general mechanism of diffusion in Hamiltonian systems. Qualitative results.” Arxiv.org/submit/0969761/pdf
[18]M. Gidea, J.-P. Marco. “Diffusion along chains of normally hyperbolic cylinders.” Preprint.
[19]M. Gidea, C. Robinson. “Diffusion along transition chains of invariant tori and Aubry–Mather sets”. Ergodic Theory and Dynamical Systems 33(5):1401–1449, 2013.
[20]V. Gelfreich, D. Turaev. “Arnold Diffusion in a priory chaotic Hamiltonian systems.” arXiv:1406.2945.
[21]M. W. Hisch, C. Pugh, M. Schub. “Invariant manifolds.” Lecture Notes in Mathematics 583, Springer-Verlag, (1977).
[22]V. Kaloshin, K. Zhang. “A strong form of Arnold diffusion for two and a half degrees of freedom.” arXiv:1212.1150.
[23]P. Le Calvez. “Drift orbits for families of twist maps of the annulus.” Ergodic Theory and Dynamical Systems 27(3):869–879, 2007.
[24]L. Lazzarini, J.-P. Marco. “From the Birkhoff theory of twist maps to Arnold diffusion in the a priori unstable case.”
[25]J.-P. Marco. “Modèles pour les applications fibrées et les polysystèmes.” C. R. Math. Acad. Sci. Paris, 346(3–4):203–208, 2008.
[26]J.-P. Marco. “Chains of compact cylinders for cusp-generic nearly integrable convex systems on ?3.” arXiv:1602.02399.
[27]J.-P. Marco. “Arnold diffusion for cusp-generic nearly integrable convex systems on ?3.” arXiv:1602.02403.
[28]J. Mather. “Arnold diffusion: announcement of results.” J. Math. Sci. (N.Y.) 124(5):5275–5289, 2004.
[29]R. Moeckel. “Generic drift on Cantor sets of annuli in Celestial mechanics.” Contemp. Math., Amer. Math. Soc., Providence, RI, 292:163–171, 2002
[30]M. Nassiri, E. Pujals. “Robust transitivity in Hamiltonian dynamics.” Annales Scientifiques de l’École Normale Supérieure 45:191–239, 2012.
[31]C. Robinson. “Generic Properties of Conservative Systems”. American Journal of Mathematics 92(3):562–603, 1970.
[32]C. Robinson. Generic Properties of Conservative Systems II R. American Journal of Mathematics 92(4):897–906, 1970.
[33]L. Sabbagh. “Inclination lemmas for normally hyperbolic invariant manifolds with applications to diffusion.” Ergodic Theory and Dynamical Systems, Available on CJO 2014 doi:10.1017/etds.2014.30.
[34]D. Salamon. “The Kolmogorov–Arnold–Moser theorem.” Math. Phys. Electron. J. 10, Paper 3, 37 pp., 2004.
[35]D. V. Treschev. “Evolution of slow variables in a priori unstable Hamiltonian systems.” Nonlinearity 17:1803–1841, 2004.












