6.1.1Introduction

Photoacoustic tomography (PAT) is a medical imaging technique that combines electromagnetic excitation (in the visible spectrum) with ultrasound measurements. In a photoacoustic experiment, a translucent sample is illuminated by a laser pulse with wavelength λ (which we assume to be fixed in this article). The absorbed optical energy leads to thermal expansion, generating an ultrasound pressure wave p(x, t) that can be measured outside the sample.

Since the pulses used in PAT are very short, the complete energy is deposited almost instantaneously compared to travel times of acoustic waves, and the pressure wave p can be assumed to have been generated by an initial pressure ℋ(x), that is, it satisfies the wave equation

and p|M, where ℳ denotes a measurement surface, can be obtained from ultrasound measurements [13, 14, 28, 45].

By solving an inverse problem for the wave equation (see, e.g, [28] for a review of inversion techniques), these ultrasound measurements can be used to estimate the initial pressure ℋ(x). Since

that is, ℋ(x) is proportional to the absorbed energy ε(x), which is in turn proportional to the optical absorption coefficient μ(x) at the applied wavelength λ and the local fluence u(x) (the time-integrated laser power received at x), the initial pressure visualizes contrast in μ. The constant of proportionality Γ(x) is called the Grüneisen coefficient (or PA efficiency since it describes the efficiency of conversion from absorbed energy to acoustic signal) [13, 14].

In quantitative photoacoustic tomography (qPAT), the goal is to apply PAT to determine (inhomogeneous) optical material properties of the sample (which are of diagnostic interest). To do so, an additional nonlinear inverse problem for light transport has to be solved, since the fluence u(x) is inhomogeneous and itself dependent on the optical properties of the sample [13, 14].

While it is also possible to attack the acoustic and optical inverse problems simultaneously (see, e.g., [9, 24]), here, we assume that the acoustic part of the problem has been solved successfully, that is that (possibly noisy) data ℋδ ≈ ℋ (with δ signifying the noise level) are available.

In this article, we utilize the diffusion approximation (which is valid in highly scattering media [13, 45]) of the radiative transfer equation to model the fluence distribution. It is, however, also possible to use a radiative transfer model for qPAT (see [17, 33, 38, 44, 46]), albeit at the cost of increased computational and analytical complexity.

The diffusion model (in a Lipschitz domain Ω ⊂ ℝN) is given by

The parameter D is called diffusion coefficient. The Dirichlet boundary data g (which we assume to be continuous and known in this article) describes the illumination pattern. Note that this is a time-independent model, again due to the fact that energy is deposited almost instantaneously compared to time scales of the acoustic system.

The difficulty of the inverse problem varies depending on which parameters of the model are assumed to be known. We present three inverse problems often considered in the literature. The hardest one is:

Bal and Ren showed in [6] that for arbitrary coefficients μ, D, Γ ∈ W1,∞(Ω), this problem is unsolvable, even if multiple measurements of ℋ (with different known boundary illumination patterns g) are available.

In [31], the authors showed that with a restriction to piecewise constant parameters, unique reconstruction of all three unknown parameters μ, D, Γ from multiple measurements is possible (under a condition on the directions of ∇uk, where uk is the fluence of the k-th illumination pattern). Furthermore, an analytical reconstruction procedure was suggested and implemented numerically, which, unfortunately, is relatively sensitive to noise.

Alberti and Ammari [1] also established a unique reconstruction result, based on morphological component analysis (a sparsity approach), in a slightly more general setting (which assumes different degrees of smoothness of the coefficients and the fluence). They also provide numerical reconstructions, which were, however, not tested for noise sensitivity in the case of (P3).

To simplify the problem, it is often assumed that the Grüneisen coefficient Γ isknown or constant, which implies that the absorbed energy can be estimated with (with δ again denoting the noise level). It remains to solve

If only a single measurement of εδ is given, this inverse problem is also ill-posed (since it has infinitely many solutions pairs, see [12, 31, 39]).

However, in [1], the authors were able to recover μ (independently of the light transfer model used) from a single measurement of ε (again using a sparsity method, assuming different degrees of smoothness of the coefficients and the fluence).

In [6, 7] it was shown that this problem is uniquely solvable if two measurements of ε (corresponding to well-chosen boundary illuminations g1, g2) are available. Numerically, this multi-illumination case was treated in [6, 22, 36, 39, 44, 48], using a multitude of different techniques, see also the review paper by Cox et al. [13].

The simplest case works under the assumption that the diffusion coefficient D is also known:

This inverse problem has a unique solution even for a single measurement, which can be seen by substituting μu = εδ in (1.2), providing the possibility to solve for u [8]. For other (numerical) approaches, cf. [13]. To the authors knowledge, this simplified problem is the only case for which practical viability (with experimental data) has been established both for phantoms [47] and biological samples [40, 41].

6.1.2Contributions of this article

In this article, we consider the problem (P2) using a single measurement for our reconstructions, a problem that is in general ill-posed. Similar to [31] (which treats (P3) with multiple measurements), a restriction to piecewise constant μ, D also proves to be useful for this problem. In fact, as shown in Section 6.2, when the parameters μ, D are piecewise constant functions (and noise-free data are given), the inverse problem (P2) can be solved uniquely, without any further assumptions.

In Section 6.3, we present a variational model for the reconstruction of piecewise constant μ, D from noisy data εδ based on the Ambrosio– Tortorelli approximation of a Mumford–Shah-like functional. Compared to the two-step reconstruction process presented in [31] (which was introduced for (P3), but is applicable for (P2)), which first detects the regions where the parameters are constant, then reconstructs the parameter values from jumps of the data and its derivatives, this variational approach is much more robust with respect to noise. This is mainly due to the fact that the numerical approach presented in [31] requires almost perfect jump detection in the second derivatives of εδ to get reasonable estimates of μ, D (since the jumps have to form a full partition of the domain Ω), which is highly challenging in the presence of significant amounts of noise. This is not the case for the variational method presented here.

Finally, a description of our implementation and numerical results can be found in Section 6.4.

6.3.1Existence of minimizers

Existence of minimizers of functionals like (3.1) (which are, in general, not unique) was first established in [18] for image segmentation and in [37] for regularization of nonlinear operator equations.

To ensure that ε(μ, D) is well defined and that ℱ has a minimizer, point-wise bounds have to be enforced (see [25]), so we have to restrict the coefficients to {f ∈ L∞(Ω) : a ≤ f ≤ b a.e. in Ω} for some 0 < a, b < ∞a priori. We also require the following Lemma, the proof follows the ideas in [19].

Lemma 3.1. The nonlinear measurement operator

where u(μ, D) solves (1.2), is continuous.

Proof. Let Furthermore, let un := u(μn, Dn) and u := u(μ, D) be solutions of (1.2) corresponding to the given coefficients.

By the usual energy estimates for (1.2) (cf. [21, Chapter 6, Theorem 2]) we have

Hence, there exists a (re-labeled) subsequence (uk )k∈ℕ with u k ⇀ u weakly in W1,2(Ω) for some u ∈ W1,2(Ω). From the weak form of (1.2) we get for all υ ∈ W1,∞(Ω) and k ∈ ℕ

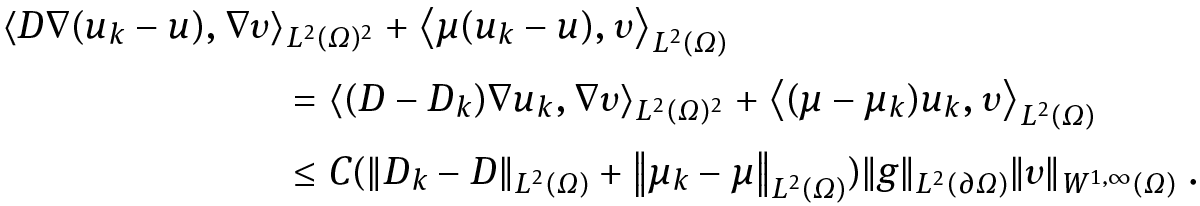
Taking k →∞and using the fact that the left side acts as a bounded linear functional on uk ∈ W1,2(Ω), we obtain for all υ ∈ W1,∞(Ω)

By density of W1,∞(Ω) ⊂ W1,2(Ω), this implies Since the same argument also holds for every subsequence of the original sequence (un)n∈ℕ, we get un ⇀ u weakly in W1,2(Ω) and thus un → u strongly in L2(Ω).

Finally, since u ∈ L∞(Ω) by the maximum principle, continuity of ε follows from

Remark 3.2. Since for all the operator L1(Ω)2 → L2(Ω) is also continuous.

Following [3, 37], we show the existence of minimizers of a weak form of ℱ defined for coefficients μ, D in the space ?ℬ?(Ω), the special functions of bounded variation, which may have jump discontinuities. For a quick introduction, see Appendix A.

We obtain the functional

where S(f) denotes the approximate discontinuity set of a Lebesgue-measurable function f and ∇μ, ∇D the density of the absolutely continuous part (with respect to the Lebesgue measure) of the respective distributional gradients (see Appendix A).

In this setting, the existence of minimizers can be established using the direct method and the ?ℬ? compactness theorem.

Proposition 3.3. The weak Mumford–Shah-like functional has at least one minimizer (μ̂ , D̂ ) in

Proof. Let be a minimizing sequence of the functional (3.2). Clearly, we have for all n ∈ ℕ

By the ?ℬ?-compactness theorem (see Section A), and using Lemma 3.1, first applied to μn, then to the obtained subsequence of Dn, there exist (μ̂ , D̂ ) ∈ ?ℬ?(Ω)2 and a subsequence (μk , D k)k∈ℕ (re-labeled) with

We also have since is closed in Furthermore, it is a minimizer of since the L2(Ω)-norm is weakly lower semi-continuous and is continuous.

6.3.2Approximation

Using the approach of Ambrosio and Tortorelli (cf. [4]), one can obtain functionals

that approximate the functional from (3.2) and are easier to minimize:

It is well known that, for all α, β > 0 and ζ = o(ϵ),

in the sense of Γ-convergence in L1(Ω) (formally, the latter has to be extended to an additional variable, see [4, 37]). Since the data term is continuous in L1(Ω) and Γ-convergence is stable under continuous perturbations, we thus get Γ-limϵ→0 ℱϵ = and therefore L1(Ω)-convergence of (a subsequence of) ℱϵ-minimizers (which can beshown to lie in a compact set [4]) to minimizers.

The existence of a minimizer of (3.3) can be established using the direct method.

Proposition 3.4. The functional ℱϵ has at least one minimizer

Proof. F ϵ is coercive with respect to the semi-norm

which, combined with the restriction shows that a minimizing sequence is bounded in W1,2(Ω)4, so it contains a subsequence that converges weakly to (μ̂ , D̂ , υ̂μ, υ̂D) in W1,2(Ω)4 (and thus strongly in L2(Ω)4). Moreover, note that the spaces and are closed in L2(Ω). The proposition follows since the discrepancy term is continuous in L2(Ω)2 and the regularization terms are weakly lower semi-continuous in W1,2(Ω)4 (cf. [15, Theorem 1.13] for the α-terms).

Remark 3.5. If we vary αμ, αD with ϵ and take

the minimizers of ℱϵ converge to piecewise constant (in ?ℬ?-sense, that is, with gradient vanishing almost everywhere) functions (μ̂ , D̂ ) that minimize

among all piecewise constant μ, D. A proof (for the single variable case) can be found in [4]. This explains, in light of Section 6.2, why this type of regularization is useful for qPAT.

6.3.3Minimization

In this subsection, we proceed formally, that is without proving convergence, existence of minimizers of sub-problems and that the necessary derivatives and adjoints exist. For the minimization of (3.3), we suggest the following alternating directions approach:

Algorithm 3.6.

We now explain the steps in more detail.

Initialization using edge detection

In our numerical simulations, it became clear that using Proposition 2.1 to obtain a reasonable estimate K ̂ of J0(μ)∪ J0(D) leads to faster convergence and better minimizers than simply taking K ̂ = 0.

Given the noisy measurements εδ, we have to estimate the discontinuities (or edges) of εδ, |∇εδ|2, and |Δεδ|. Since the jumps in these functions are of multiplicative nature (proportional to the local value of u or ∇u ⋅ ν), it is advantageous to apply a logarithmic transformation prior to edge detection (to obtain constant contrast), see [31].

Because of noise, the data has to be smoothed prior to taking derivatives (turning discontinuities into areas with large gradients). We smooth by convolution with a Gaussian, since this approach has the advantage that differentiation and smoothing can be done in one step (by differentiating the low-pass filter instead of the function). We have

Similar to [31], we proceed as follows:

Here, 1B acts as a cut-off function for the filters (e.g., using ρ the p-norm ball of radius ρ). The operation A ⊖ B = {z ∈ Ω | (B + z) ⊂ A} denotes set erosion, which is performed to avoid multiple detection of edges (by ensuring that the cut-off filter does not intersect with already detected edges or the outside of the domain). Note, however, that for large B thismay lead to parts of edges (close to the domain boundary or already detected edges) not being detected. The scalar γ is a minimal value enforced for |∇εδ|2 (to avoid creating singularities at zeros).

The edge detection itself is performed by applying thresholds ξ0 , ξ1, ξ2 to the functions |∇f0|, |∇f1|, |∇f2| (taking the super-level sets as edge sets). Note that in contrast to [31], no complete segmentation is necessary and cruder edge estimates suffice, that is, the detected edges don’t have to be reduced to thin curves.

Iteration

In step (i), to find, for fixed

we use Gauss–Newton-minimization. That is, in every iteration of an inner loop, we linearly approximate ε(μk + sμ , Dk + sD) ≈ ε(μk , Dk) + ε′(μk , Dk)(sμ , sD) and take update steps

which we then project into so we update with

A straightforward calculation shows that a minimizer s = (sμ , s D) of (3.4) satisfies the weak form of

with homogeneous Neumann boundary conditions for sμ, s D and

The linear operator ε′(μ, D) and its (formal) adjoint ε′(μ, D)∗ are given by

where u = u(μ, D) and

By introducing auxiliary variables y1, y2, y3 (and taking μ = μk , D = Dk), the equations (3.5),(3.6) can be re-written as the system of (weak) PDE

which is amenable to discretization as a sparse matrix using, for example the finite element method (FEM).

In step (ii) of the outer loop we have to find, for fixed

The minimizer (υμ, υD) satisfies the linear equations

which can be solved separately and implemented numerically using FEM.