Wave Transformation near Coasts
Abstract
A first part of the chapter deals with wave refraction before a coast. Effects on wave heights and wave directions are dealt with analytically for the case of straight contour lines, and the numerical approach is explained in detail for arbitrary contour lines. The second part of the chapter is devoted to the problem of shoaling and set-down (or set-up) of waves on a current. The way to calculate the current effect on wavelength and wave height is shown. A FORTRAN program is given and applied to a worked example of calculation of the Froude–Krylov force on a submerged tunnel across a strait with waves and current.
Keywords
Coast; Froude–Krylov force; Strait; Submerged tunnel; Wave-current; Wavelength; Wave height; Wave orthogonal; Wave refraction2.1. Refraction with Straight Contour Lines
![]() (2.1)
(2.1)
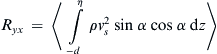 (2.2)
(2.2)

![]() (2.3)
(2.3)
![]() (2.4)
(2.4)
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)

![]() (2.7)
(2.7)
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
![]() (2.10)
(2.10)
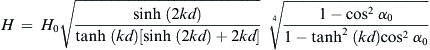 (2.11)
(2.11)
![]() (2.12)
(2.12)
2.2. Refraction with Arbitrary Contour Lines
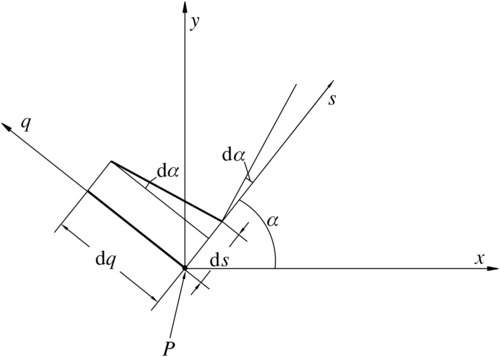
2.2.1. Wave Orthogonals
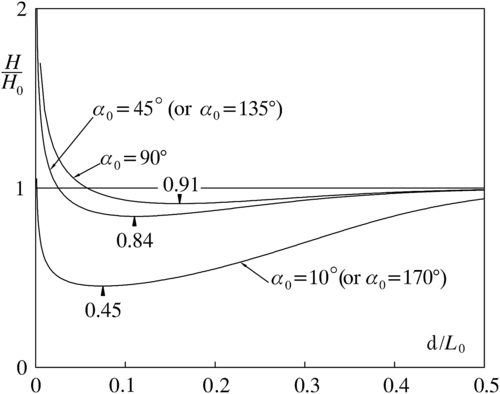
 (2.13)
(2.13)
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
![]() (2.21)
(2.21)
![]() (2.22)
(2.22)
2.2.2. Effects on the Wave Height
![]() (2.23)
(2.23)
 (2.24)
(2.24)
2.3. Wave–Current Interaction in Some Straits
2.3.1. Current Only
| S | the difference between the still water level and the actual water level; |
| d | the depth of the still water; |
| the water depth; and | |
| the velocity of the current. |

![]() (2.25)
(2.25)
![]() (2.26)
(2.26)
![]() (2.27)
(2.27)
![]() (2.28)
(2.28)
![]() (2.29)
(2.29)
2.3.2. Current + Waves: The Wavelength
![]() (2.30)
(2.30)
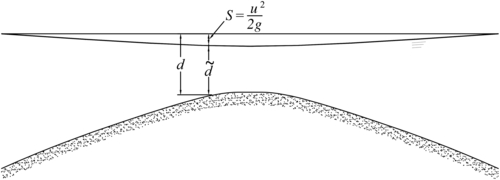
![]() (2.31)
(2.31)
![]() (2.32)
(2.32)
![]() (2.33)
(2.33)
![]() (2.34)
(2.34)
![]() (2.35)
(2.35)
![]() (2.36)
(2.36)
2.3.3. Current + Waves: The Wave Height

![]() (2.37)
(2.37)
![]() (2.38)
(2.38)
![]() (2.39)
(2.39)
![]() (2.40)
(2.40)
![]() (2.41)
(2.41)
![]() (2.42)
(2.42)
![]() (2.43)
(2.43)
![]() (2.44)
(2.44)
![]() (2.45)
(2.45)
![]() (2.46)
(2.46)
![]() (2.47)
(2.47)
![]() (2.48)
(2.48)
![]() (2.49)
(2.49)
![]() (2.50)
(2.50)
![]() (2.51)
(2.51)
![]() (2.52)
(2.52)
![]() (2.53)
(2.53)
2.4. Worked Example

![]() (2.54)
(2.54)
![]() (2.55)
(2.55)
PROGRAM CURRENT
DIMENSION AV(1000),BV(1000),DV(1000),GV(1000),FV(1000)
DIMENSION DELTAV(1000),RKCIV(1000),DSTIV(1000)
PG=3.141592
DPG=2.∗PG
DG=2.∗9.8
RO=1030.
WRITE(6,∗)'d,zitac,diam'
READ(5,∗)D,ZITAC,DIAM
ZC=D-ZITAC
.RAGG=DIAM/2.
AREA=PG∗RAGG∗RAGG
WRITE(6,∗)'H0,T'
READ(5,∗)H0,T
OM=DPG/T
WRITE(6,∗)'Q m3/s/m (positive or negative)'
READ(5,∗)Q
TOLL=1.E-6
IF(Q.EQ.0)Q=TOLL
c preliminary control
QMAX=SQRT(2.∗9.8∗D)∗D∗2./SQRT(27.)
IF(ABS(Q).GT.QMAX)STOP
N=200
DD=1
DO 100 I=1,N
c loop 100: growing water depths
DI=D+FLOAT(I-1)∗DD
DV(I)=DI
c step 1): ui
QI=SQRT(2.∗9.8∗DI)∗DI
X=1
DX=0.01
QQ=(Q/QI)∗∗2
90 X=X+DX
F1=X
F2=1.+QQ∗X∗X∗X
IF(F1.LT.F2)GO TO 90
X=X-DX
DX=DX/10.
IF(DX.GT.2.E-5)GO TO 90
UI=(Q/DI)∗X
SI=UI∗UI/DG
DSTI=DI-SI
DSTIV(I)=DSTI
c step 2):Lci (RLCI)
RL0=1.56∗T∗T
C0=RL0/T
UC0I=UI/C0
DL0I=DSTI/RL0
AI=UC0I∗UC0I/DL0I
.BI=DL0I/UC0I
DX=0.01
X=0
80 X=X+DX
IF(X.GT.10)THEN
WRITE(6,∗)'the wave cannot travel against the current'
STOP
ENDIF
F1=X∗TANH(DPG∗X)
F2=AI∗(X-BI)∗∗2
IF(F1.LT.F2)GO TO 80
X=X-DX
DX=DX/10.
IF(DX.GT.2.E-5)GO TO 80
RLCI=DSTI/X
RKCI=DPG/RLCI
RKCIV(I)=RKCI
c DI=di, UI=ui, SI=si, DSTI =diˆ, RLCI=lci, RKCI=kci
OI=1./(OM-UI∗RKCI)
COSA=COSH(RKCI∗DSTI)
CHI=COSA∗COSA
SHI=SINH(2.∗RKCI∗DSTI)
IF(RKCI∗DSTI.LT.10)THEN
AD1=(1./16.)∗9.8∗OI∗OI∗UI∗RKCI∗RKCI∗DSTI/CHI
AD2=(1./32.)∗9.8∗((2.∗RKCI∗DSTI+SHI)/CHI)∗OI∗(1.+UI∗RKCI∗OI)
RKI=AD1+AD2+UI/8.
ELSE
AD1=0
AD2=(1./32.)∗9.8∗2.∗OI∗(1.+UI∗RKCI∗OI)
RKI=AD1+AD2+UI/8.
ENDIF
AI=((1./16.)∗9.8∗H0∗H0/OM-0.5∗PG∗SI∗H0∗H0/T)/RKI
BI=(2.∗SI∗UI-Q)/RKI
CI=-H0∗H0/16.+0.5∗PG∗(UI/9.8)∗H0∗H0/T
DI=1./16.+(1./8.)∗9.8∗OI∗OI∗RKCI∗RKCI∗DSTI/CHI
EI=-3.∗SI
FI=CI+AI∗DI
GI=BI∗DI+EI
c store on memory the values of AI, BI, FI, GI
AV(I)=AI
BV(I)=BI
.FV(I)=FI
GV(I)=GI
100 CONTINUE
c step 4): obtain the sequence deltai from i=N-1 to i=1
I=N
DELTAV(N)=0
200 I=I-1
DI=DV(I)
DI1=DV(I+1)
DELTAI1=DELTAV(I+1)
FI=FV(I)
FI1=FV(I+1)
GI=GV(I)
GI1=GV(I+1)
RNUM=0.5∗(DI+DI1)∗DELTAI1-FI+FI1+GI1∗DELTAI1
DEN=GI+0.5∗(DI+DI1)
DELTAV(I)=RNUM/DEN
IF(I.EQ.1)GO TO 201
GO TO 200
201 CONTINUE
c step 5): obtain wave height H on the given water depth d
DELTA1=DELTAV(1)
A1=AV(1)
B1=BV(1)
H=SQRT(A1+B1∗DELTA1)
c delta1 is the wave set-down (or set-up) on the given water depth d
WRITE(6,7003)DELTA1
7003 FORMAT(/,1X,'DELTA ',F7.3)
c particle acceleration of waves on current
RKCI=RKCIV(1)
DSTI=DSTIV(1)
RLCI=DPG/RKCI
ATTC=COSH(RKCI∗ZITAC)/COSH(RKCI∗DSTI)
AYC=9.8∗0.5∗H∗RKCI∗ATTC
ATTC1=SINH(RKCI∗ZITAC)/COSH(RKCI∗DSTI)
AZC=9.8∗0.5∗H∗RKCI∗ATTC1
c Froude-Krylov force on the submerged tunnel:
FYC=RO∗AREA∗AYC/1.E3
FZC=RO∗AREA∗AZC/1.E3
c particle acceleration without the current
RL0=1.56∗T∗T
RLI1=RL0
70 RLI=RL0∗TANH(DPG∗D/RLI1)
TEST=ABS(RLI-RLI1)/RLI
RLI1=RLI
IF(TEST.GT.1.E-4)GO TO 70
RL=RLI
RK=DPG/RL
SINA=SINH(2.∗RK∗D)
TANA=TANH(RK∗D)
ARG=SINA/(TANA∗(SINA+2.∗RK∗D))
CSHO=SQRT(ARG)
c CSHO shoaling coefficient
HH=H0∗CSHO
ATT=COSH(RK∗ZITAC)/COSH(RK∗D)
AY=9.8∗0.5∗HH∗RK∗ATT
ATT1=SINH(RK∗ZITAC)/COSH(RK∗D)
AZ=9.8∗0.5∗HH∗RK∗ATT1
c Froude-Krylov force on the submerged tunnel, without the current:
FY=RO∗AREA∗AY/1.E3
FZ=RO∗AREA∗AZ/1.E3
WRITE(6,∗)
WRITE(6,2000)FYC,FY
2000 FORMAT(15X,'fy',7X,F7.0,7X,F7.0)
WRITE(6,2001)FZC,FZ
2001 FORMAT(15X,'fz',7X,F7.0,7X,F7.0)
WRITE(6,2002)H,HH
2002 FORMAT(15X,'H',10X,F6.1,8X,F6.1)
WRITE(6,2003)RKCI,RK
2003 FORMAT(15X,'k',7X,F7.4,7X,F7.4)
WRITE(6,2004)ATTC,ATT
2004 FORMAT(15X,'AF(ø)',3X,F7.4,7X,F7.4)
WRITE(6,∗)
WRITE(6,∗)'(ø) AF=attenuation factor'
END
| With the Current | Without the Current | |
| fy (kN/m) | 419 | 344 |
| fz (kN/m) | 409 | 321 |
| H (m) | 19.5 | 14.8 |
| k (m−1) | 0.0363 | 0.0282 |
| AF (°) | 0.2383 | 0.3339 |
(°) AF = Depth attenuation factor.