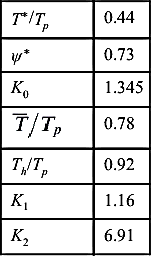Wave Statistics in Sea States
Abstract
The first two sections are devoted to the basic concepts on stationary Gaussian processes. These concepts are then used to deduce Rice's solution (1958) for the expected number per unit time of b up-crossings of the random surface elevation (with b being any fixed threshold). The chapter goes on to show three corollaries of this solution, including the distribution of wave height under narrowband assumption. Then, the chapter shows some important consequences of the quasi-determinism theory on wave statistics. The conclusive part of the chapter deals with the calculation of the maximum expected wave in a sea state of given significant wave height, duration, and shape of the spectrum. Three FORTRAN programs useful for this calculation are supplied and discussed. A fresh point of view (2013) of an old subject (wave height distribution: bandwidth and third-order nonlinearity effects) is dealt with in the conclusion to the chapter.
Keywords
Average wave period; Bandwidth effect; Maximum expected wave height; Nonlinearity effect; Period largest waves; QD theory; Sea state; Small-scale field experiment (SSFE); Wave height distribution4.1. Surface Elevation as a Stationary Gaussian Process
4.1.1. The Probability of the Surface Elevation
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
4.1.2. Proof Relevant to Any Given Realization
![]() (4.4)
(4.4)
![]() (4.5)
(4.5)
![]() (4.6)
(4.6)
 (4.7)
(4.7)
![]() (4.8)
(4.8)
4.1.3. Proof Relevant to the Ensemble at a Fixed Time Instant
 (4.9)
(4.9)
![]() (4.10)
(4.10)
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
![]() (4.13)
(4.13)
4.2. Joint Probability of Surface Elevation
![]() (4.14)
(4.14)
![]() (4.15)
(4.15)
![]() (4.16)
(4.16)
![]() (4.17)
(4.17)
 (4.18)
(4.18)
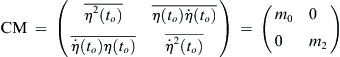 (4.19)
(4.19)
 (4.20)
(4.20)
4.3. Rice's Problem (1958)
![]() (4.21)
(4.21)
 (4.22)
(4.22)
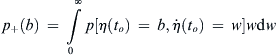 (4.23)
(4.23)
![]() (4.24)
(4.24)

![]() (4.25)
(4.25)
![]() (4.26)
(4.26)
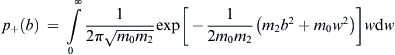 (4.27)
(4.27)
![]() (4.28)
(4.28)
![]() (4.29)
(4.29)
4.4. Corollaries of Rice's Problem
4.4.1. Probability of Crest Height and Wave Height
![]() (4.30)
(4.30)
![]() (4.31)
(4.31)
![]() (4.32)
(4.32)
![]() (4.33)
(4.33)
![]() (4.34)
(4.34)
![]() (4.35)
(4.35)
4.4.2. The Mean Wave Period
![]() (4.36)
(4.36)
![]() (4.37)
(4.37)
 (4.38)
(4.38)
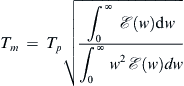 (4.39)
(4.39)
![]() (4.40)
(4.40)
4.5. Consequences of the QD Theory onto Wave Statistics
4.5.1. Period Th of a Very Large Wave
![]() (4.41)
(4.41)
![]() (4.42)
(4.42)
 (4.43)
(4.43)
4.5.2. The Wave Height Probability under General Bandwidth Assumptions

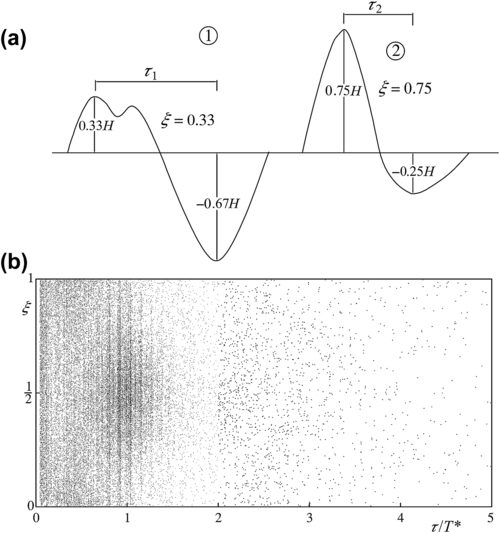
![]() (4.44)
(4.44)
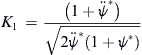 (4.45)
(4.45)
![]() (4.46)
(4.46)
![]() (4.47)
(4.47)
 (4.48)
(4.48)
![]() (4.49)
(4.49)

![]() (4.50)
(4.50)
![]() (4.51)
(4.51)
![]() (4.52)
(4.52)
4.6. Field Verification
4.6.1. An Experiment on Wave Periods
4.6.2. The Random Variable β
![]() (4.53)
(4.53)
![]() (4.54)
(4.54)
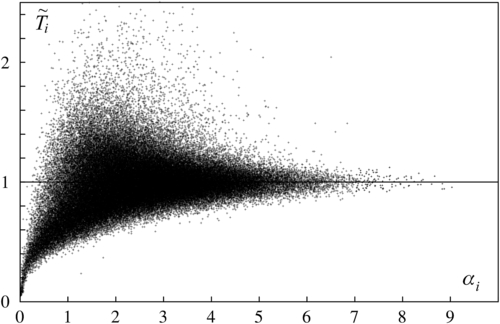
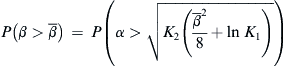 (4.55)
(4.55)
 (4.56)
(4.56)

 from a small-scale field experiment of 2010 on a very large variety of spectra, with a total number of 6,300,000 individual waves.
from a small-scale field experiment of 2010 on a very large variety of spectra, with a total number of 6,300,000 individual waves.4.7. Maximum Expected Wave Height and Crest Height in a Sea State of Given Characteristics
4.7.1. The Maximum Expected Wave Height
![]() (4.57)
(4.57)
![]() (4.58)
(4.58)
 (4.59)
(4.59)
 (4.60)
(4.60)
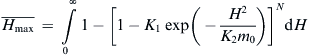 (4.61)
(4.61)
4.7.2. Maximum Expected Crest Height
 (4.62)
(4.62)
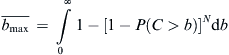 (4.63)
(4.63)
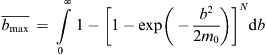 (4.64)
(4.64)
4.8. FORTRAN Programs for the Maximum Expected Wave in a Sea State of Given Characteristics
4.8.1. A Program for the Basic Parameters on Deep Water
PROGRAM SUMMARY
DIMENSION EW(500),WV(500)
DIMENSION TAUV(200),ETADET(200),TZU(5)
PG=3.141592
DPG=2.∗PG
WRITE(6,∗)'chi1,chi2'
READ(5,∗)CHI1,CHI2
C1=ALOG(CHI1)
C2=2∗CHI2∗CHI2
WIN=0.5
WMAX=5
DW=0.02
W=WIN-DW/2
I=0
90 W=W+DW
IF(W.GT.WMAX)GO TO 91
I=I+1
WM1=W-1
W2=W∗W
W4=W2∗W2
W5=W4∗W
ARG3=WM1∗WM1/C2
E3=EXP(-ARG3)
ARG2=C1∗E3
E2=EXP(ARG2)
ARG1=1.25/W4
E1=EXP(-ARG1)
c values of w and E(w) stored on memory
WV(I)=W
EW(I)=E1∗E2/W5
GO TO 90
91 CONTINUE
IMAX=I
c calculation of T∗/Tp and psi∗
PSIMIN=0
DTAU=0.01
TAU=-DTAU
70 TAU=TAU+DTAU
c Loop 70 tau (=T/Tp) from 0 to 1
IF(TAU.GT.1) GO TO 71
SOMT=0
SOM0=0
DO 75 I=1,IMAX
c Loop 75 over the stored values of w and E(w)
W=WV(I)
COSA=COS(DPG∗W∗TAU)
SOMT=SOMT+EW(I)∗COSA∗DW
SOM0=SOM0+EW(I)∗DW
75 CONTINUE
PSI=SOMT/SOM0
c PSI=psi(T)/psi(0)
IF(PSI.LT.PSIMIN)THEN
PSIMIN=PSI
TAUMI=TAU
ENDIF
GO TO 70
71 CONTINUE
TASTP=TAUMI
PSIAS=ABS(PSIMIN)
c TASTP=T∗/Tp
c PSIAS=psi∗
SOM0=0
DO I=1,IMAX
SOM0=SOM0+EW(I)∗DW
ENDDO
RK0=1./SOM0∗∗0.25
SOM0=0
SOM2=0
DO I=1,IMAX
W=WV(I)
.SOM0=SOM0+EW(I)∗DW
SOM2=SOM2+EW(I)∗W∗W∗DW
ENDDO
TMTP=SQRT(SOM0/SOM2)
c TMTP=Tm/Tp
c calculation of Th/Tp
DTAU=0.01
TAUI=-0.5
TAUF=1
TAU=TAUI-DTAU
J=0
80 TAU=TAU+DTAU
c Loop 80: TAU=T/Tp from -0.5 to 1
IF(TAU.GT.TAUF)GO TO 81
J=J+1
SOM1=0
SOM2=0
DO I=1,IMAX
W=WV(I)
ARG1=DPG∗W∗TAU
ARG2=DPG∗W∗(TAU-TASTP)
ARG3=DPG∗W∗TASTP
SOM1=SOM1+EW(I)∗(COS(ARG1)-COS(ARG2))∗DW
SOM2=SOM2+EW(I)∗(1-COS(ARG3))∗DW
ENDDO
ETADET(J)=0.5∗SOM1/SOM2
TAUV(J)=TAU
c TAUV(J)=T/Tp
GO TO 80
81 CONTINUE
JMAX=J
NZU=0
DO 65 J=2,JMAX
TAU=TAUV(J)
IF(ETADET(J).GE.0.AND.ETADET(J-1).LT.0)THEN
NZU=NZU+1
E1=-ETADET(J-1)
E2=ETADET(J)
TZU(NZU)=TAU-DTAU+DTAU∗E1/(E1+E2)
.ENDIF
65 CONTINUE
THTP=TZU(2)-TZU(1)
c THTP=Th/Tp
SOM1=0
SOM2=0
DO I=1,IMAX
W=WV(I)
W2=W∗W
ARG=DPG∗W∗TASTP
COSA=COS(ARG)
SOM1=SOM1+EW(I)∗W2∗COSA∗DW
SOM2=SOM2+EW(I)∗W2∗DW
ENDDO
PSIS=ABS(SOM1/SOM2)
c PSIS=psi..∗
RNUM=1+PSIS
RDEN=SQRT(2.∗PSIS∗(1.+PSIAS))
RK1=RNUM/RDEN
RK2=4.∗(1.+PSIAS)
WRITE(6,1001)TASTP
WRITE(6,1002)PSIAS
WRITE(6,1003)RK0
WRITE(6,1004)TMTP
WRITE(6,1005)THTP
WRITE(6,1006)RK1
WRITE(6,1007)RK2
1001 FORMAT(2X,'T∗/Tp ',f7.2)
1002 FORMAT(2X,'psi∗ ',f7.2)
1003 FORMAT(2X,'K0 ',f7.3)
1004 FORMAT(2X,'Tm/Tp ',f7.2)
1005 FORMAT(2X,'Th/Tp ',f7.2)
1006 FORMAT(2X,'K1 ',f7.2)
1007 FORMAT(2X,'K2 ',f7.2)
END
4.8.2. A Program for the Basic Parameters on a Finite Water Depth, Using the Shape of the TMA Spectrum
EW(I)=E1∗E2/W5
EW(I)=TFU(W,DLP0)∗E1∗E2/W5
FUNCTION TFU(w,DLP0)
PG=3.141592
DPG=2.∗PG
W2=W∗W
DX=1
X=0
110 X=X+DX
F=X∗TANH(DPG∗X∗DLP0)
IF(F.LT.W2)GO TO 110
X=X-DX
DX=DX/10.
IF(DX.GT.2.E4)GO TO 110
RKW=X
c RKW=kw
ARG=4.∗PG∗RKW∗DLP0
IF(ARG.LT.30.)THEN
SI2=SINH(ARG)
DEN=SI2+ARG
RMOL=SI2/DEN
ARG=ARG/2
TA=TANH(ARG)
TFU=TA∗TA∗RMOL
ELSE
TFU=1
ENDIF
RETURN
END
4.8.3. A Program for the Maximum Expected Wave Height
PROGRAM HMAX
DOUBLE PRECISION UPH,PC,PDBLE
CHARACTER∗64 NOMEC
NOMEC='PROHMAX'
OPEN(UNIT=66,FILE=NOMEC)
WRITE(6,∗)'Hs,N'
READ(5,∗)HS,N
WRITE(6,∗)'K1,K2'
READ(5,∗)RK1,RK2
SIG=HS/4.
RM0=SIG∗SIG
DH=0.10
HMA=0
c HMA value of the integral to be executed in the loop 90
.90H=H+DH
IF(H.GT.3.∗HS)GO TO 91
ARG=H∗H/(RK2∗RM0)
EE=EXP(-ARG)
PH=RK1∗EE
UPH=1.-DBLE(PH)
PC=UPH∗∗N
PDBLE=1.-PC
P=PDBLE
c P=P(Hmax>H)
WRITE(66,1010)H,P
1010 FORMAT(2X,F7.2,2X,E12.4)
HMA=HMA+P∗DH
GO TO 90
91 CONTINUE
WRITE(6,1000)HMA
1000 FORMAT(2X,'Hmax ',f7.2)
WRITE(6,∗)'read file prohmax'
END
4.8.4. Worked Example
![]()
![]()
![]()
![]()
![]()

4.9. Conclusion
![]() (4.65)
(4.65)
![]() (4.66)
(4.66)
![]() (4.67)
(4.67)
![]() (4.68)
(4.68)
![]() (4.69)
(4.69)
![]()